基于深度学习的超分辨率重构方法在CAARC标模绕流流场重构中的应用

梁仍康，张 伟，杨思帆，黄 刚，李 朗

(1.西南科技大学 土木工程与建筑学院，绵阳 621010；2.中国空气动力研究与发展中心 超高速空气动力研究所，绵阳 621000；3.空天飞行空气动力科学与技术全国重点实验室，绵阳 621000)

0 引言

随着建筑技术的进步，众多建筑结构向着长细化、高耸化、轻质化等方向发展，这使得风荷载对建筑结构的影响增大。风荷载逐步成为高层建筑结构安全性、舒适性和经济性等需要考虑的主要因素[1]，甚至是影响高层建筑物安全的决定性因素。因此高层建筑的风荷载及其风振响应研究成为结构风工程中的重点，许多学者采用CFD 数值模拟或风洞试验等方法对其开展了大量研究[2-5]。

精细化高分辨率的风场数据是结构设计所必需的。在工业中，人们期望以更少的代价快速获取高分辨率(high resolution,HR)流场数据。但在试验方面，精细化的测量点必然导致试验成本显著增加；在计算方面，网格细化是获取高分辨率数据的直接方法，但数值模拟的计算成本可能会呈指数增长。开发一种有效的方法来获取HR 数据变得非常重要。深度学习具有计算过程简单、速度快的优点，得益于当前丰富的试验和计算数据，利用深度学习方法来快速实现超分辨率重构工作变得可能。

超分辨率(super-resolution,SR)技术[6]是指根据低分辨率图像重构出相应的高分辨率图像。传统图像SR 算法可分为基于插值[7]和重构[8]的方法，在基于插值的超分辨率重构方法中，双三次插值算法（Bicubic）是一种高精度的重构方法，被广泛应用于图像和数据的处理中。但是传统方法会存在一些不足，如会造成边缘模糊、无法处理复杂结构的图像等。为了解决传统图像SR 方法的不足，出现了采用深度学习[9-10]进行超分辨率分析的研究，并在图像处理的任务中取得了显著效果。Dong 等[10-11]提出的超分辨率卷积神经网络(super-resolution convolutional neural network,SRCNN)是基于深度学习的超分辨率分析的先驱。近年来，基于深度学习的超分辨率重构方法被拓展到流体力学领域。2019 年，Fukami 等[12-13]率先将基于卷积神经网络（convolutional neural network,CNN）的超分辨率重构模型应用于二维圆柱尾迹和二维衰减各向同性湍流，结果显示出该模型从低分辨率流场数据中重构流场的能力显著。Liu 等[14]针对均匀各向同性湍流和槽道流的超分辨率重构问题，提出了静态卷积神经网络(static convolutional neural network,SCNN)和多时间路径卷积神经网络(multiple temporal paths convolutional neural network,MTPC)两种深度学习模型。Kim[15]提出了一种无监督学习模型，该模型采用循环一致生成对抗网络(cycle-consistent generative adversarial network,CycleGAN)，可以用未配对湍流数据进行训练，进行超分辨率重构。

综上，基于深度学习的超分辨率重构方法在提高试验或数值模拟数据质量方面已显示出巨大的潜能[16]，但以往工作主要针对几何构型相对简单的模型流动，如圆柱绕流、槽道湍流等，针对建筑结构复杂风场的超分辨率重构尚未见系统研究报道。而高雷诺数下具有多尺度湍流特征的建筑结构绕流流场的复杂性，也为深度学习模型的构建带来了新的挑战。基于此，本文将基于深度学习的超分辨率重构方法应用到CAARC (Commonwealth Advisory Aeronautical Research Council)标准建筑模型[17]绕流流场，构建其超分辨率重构的深度学习模型，并通过算例分析采用该方法对建筑结构绕流欠分辨率流场信息重构高分辨流场的可行性和有效性。

1 研究方法

深度学习的任务通常是通过数据学习来建立映射关系y=F(x,w)，其中y是输出，x是输入，w是权重参数，F是非线性映射。对于超分辨率任务来说，x对应低分辨率数据，y对应高分辨率数据，权重w是通过梯度下降算法求解优化来确定的。通过深度学习数据库得到w后，即可建立模型F。采用深度学习方法实现流场超分辨率重构的主要流程如图1 所示。其中，3 表示3 个通道数，32×32、64×64 分别为输入和输出图片的像素。

为了准备输入数据，采用下采样的方式来获得低分辨率数据，下采样主要通过最大池化或平均池化来实现，对应公式为：

其中，LR 和HR 分别表示低分辨率和高分辨率，i和j表示x、y方向的点，池化窗口大小为M×M，P取1 或∞分别对应平均池化和最大池化，“p,s”为“i,j”对应的高分辨率图像区域的空间点编号。本文中，输入层的低分辨数据通过平均池化方法对原始高分辨率数据（Lh×Lw×C，Lh、Lw和C分别为数据高度、数据宽度和数据通道数）进行下采样获得，下采样比为M，则下采样后的低分辨率数据的尺寸为(Lh/M)×(Lw/M)×C；池化使得原先Lh×Lw（本文为64×64）像素数据变成 (Lh/M)×(Lw/M) 像素。本文的M值有3 个，分别为2、4、8，对应的输入分辨率分别为32×32、16×16 和8×8。

通过CNN 来建立非线性映射F，卷积神经网络内前后两层的数据传递关系可以表示为：

达到最后一层时就得到输出结果。以三层CNN(lmax=3)为例，如图2 所示，h表示滤波器，φ表示激活函数，l表示卷积神经网络的某一层，m对应滤波器的个数，L(Lh=Lw) 是每个方向上的像素数，K表示构成数据的图像数。对流场进行超分辨率重构时，选择速度分量、压力系数作为输入，对应K可以选择1、2、3、4 等值。本文使用双曲正切Tanh 作为激活函数，其可以有效地在深度学习过程中稳定权重更新；模型预测值与标准实际值的平均绝对误差作为损失函数。

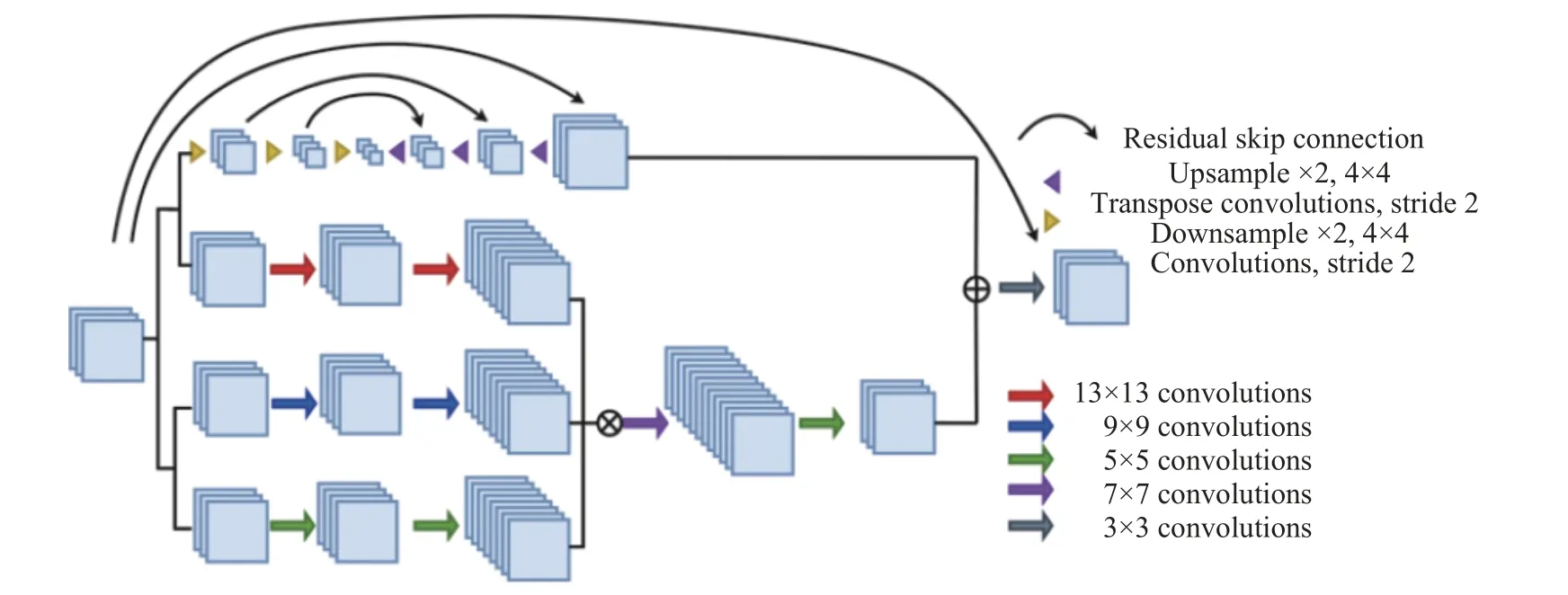
图2 卷积神经网络架构Fig.2 Architecture of convolutional neural network

原始的卷积神经网络由5 个不同大小的卷积核组成。输入的低分辨率图像经过卷积层进行特征提取，池化层降低了每个特征图的维度，但是保留了最重要的信息，全连接层卷积、池化等层计算得到的特征空间映射到样本标记空间，最终输出超分辨重构的图像。

为了实现更优的流场超分辨率重构效果，本文对原始的CNN 模型加以改进，改进后为混合下采样跳跃连接多尺度（Multi-scale CNN）模型。首先，引入压缩和跳跃连接来扩展CNN 模型。在超分辨率分析中，数据压缩提高了对数据元素平移和旋转的鲁棒性。使用跳跃连接帮助加速权重收敛增强了CNN 预测性能，使得CNN 不受网络深度的制约。其次，考虑多尺度模型，该模型能有效捕捉数据中的多尺度结构。该多尺度模型是由多个CNN 滤波器组成，这些滤波器具有不同的长度，以跨越一系列尺度。本文使用的超分辨率方法结合了跳跃连接和多尺度两种模型，方法的完整示意图如图2 所示，包括：1）1 个下采样和上采样路线，其目的为增加鲁棒性；2）3 个不同卷积核的卷积层，不同卷积核用来捕捉流场中不同湍流尺度的结构；3）跳跃连接，其目的是更好地训练深层网络，并确保网络能在添加更多层时得到有效训练。

2 计算模型与数值模拟

CAARC 高层建筑标准模型是1969 年提出的通用风工程标准模型，其几何尺寸为30.5 m（宽度B）×45.7 m（长度D）× 182.5 m（高度H）。本文基于Elshaer 等[18]的文献，将CAARC 建筑模型进行1∶400的缩比处理。建筑模型绕流流场计算域、局部网格划分以及两种不同来流风向角工况如图3 所示，其三维计算域为 [-4.05,4.05]×[-3.195,10.4075]×[0,2.2825]。流动方向是y方向，梯度风速度入口条件如下：

图3 计算流域、网格划分以及来流风向角工况示意图Fig.3 Schematic of computational setup of CAARC model and two wind angles of attack

其中，Uavref=10 m/s，zref=0.45625 m，α=0.17，z是高度。采用随机生成方法，并通过使用傅里叶谐波合成无散速度场来生成来流速度脉动量。入口速度及次网格滤波长度见图4。计算域侧面及顶面为对称面，出口边界为压力出口，建筑表面和下边界是静止无滑移壁面。采用分块结构网格对计算域进行网格划分，建筑表面第一层边界层高度是2×10-5m，网格总数约150 万。

图4 湍流特性Fig.4 Characteristic of turbulent flow

计算采用基于压力的瞬态隐式算法求解器，采用SIMPLEC 算法[19]实现压力与速度的解耦。方程中压力项的离散采用标准格式，动量、湍动能的离散均采用二阶迎风格式。采用WMLES S-Omega 亚格子模型的大涡模拟计算湍流流场。各变量的计算收敛误差均设定为1×10-5，时间步长为0.005 s。

为验证CFD 结果的可靠性，图5 给出了来流为0°风向角（工况一）时，数值计算的CAARC 建筑模型2/3 高度处的压力系数平均值及均方根值与风洞试验结果[18]的对比，其中横坐标表示长度与建筑宽度的比值。压力系数公式为：

图5 当前研究与实验的压力系数对比Fig.5 Comparison of pressure coefficients between current simulation and experiment

其中，vh=10 m/s 是建筑物高度的参考速度，p为静压，p0为参考压强，ρ是空气密度。由图5 可见，CFD 计算结果与试验结果基本吻合。

同时，对比了建筑的顺风向及横风向力系数（图6），其定义分别为：

图6 顺风向及横风向力系数随时间的变化规律Fig.6 Evolution of along-wind force and cross-wind force coefficient in function of time

其中，Fy、Fx分别表示建筑的顺风向及横风向力。

表1 给出了顺风向及横风向力系数的平均值和均方根值，结果与Thordal 等[20-22]总结的结果基本吻合。

表1 不同来源的顺风向与横风向力系数对比Table 1 Comparison of along-wind force and cross-wind force coefficient with different sources

3 流场的超分辨率重构

基于工况一的CFD 计算结果，待流场计算相对稳定后，每隔0.005 s 输出一个流场数据，取120 个数据构建数据集。120 个样本选自t=40 s 后的时间段，时间跨度为0.6 s，约4.7 个卡门涡街周期[23]。在进行模型训练之前，数据进行了归一化处理。随机取100 个数据作为训练集，20 个数据作为测试集；训练次数为600 次，卷积层数共14 层，学习率取0.002 5。

3.1 风压场的超分辨率重构

风压场的数据取自建筑模型迎风面、侧面和背面的压力场。为了验证本文的Multi-scale CNN 模型针对风压场超分辨率重构的有效性，首先以32 × 32 低分辨率风压场重构64 × 64 高分辨率风压场作为验证。图7 给出了风压场训练误差和测试误差随着训练步数的变化，可以看出两者都随训练步数的增加不断减少，大约在315 步后接近平稳，平稳后的训练误差约为0.22%，测试误差约为0.48%。由于模型的泛化性能，测试误差始终比训练误差略微偏大。图8 给出了建筑侧面压力云图随训练步数增加的变化过程。可以看出，初始输出的压力场是粗糙不规则的。当训练步数为200 时，训练结果与CFD 模拟标准结果还有一定差别；随着训练步数继续增加，训练结果与CFD 模拟的标准结果的差距逐渐缩小；训练步数为400 时，侧面压力云图已经接近真实值。

图7 建筑表面风压场的超分辨率训练误差下降过程Fig.7 Super-resolution learning error of wind pressure field

图8 建筑侧面压力系数在不同训练步数的结果Fig.8 Pressure coefficients contours on the lateral face as the epoch increases

为进一步验证本文深度学习模型超分辨率重构压力场的优势，对不同低分辨率风压场开展了超分辨率重构，并将不同低分辨率风压场重构后的结果与原始的CNN 结果以及双三次插值结果进行了对比。输入的低分辨率风压场分辨率分别为8 × 8、16 × 16、32 ×32，重构的风压场分辨率为64 × 64。

取建筑迎风面2/3 高度(0.304 16 m)处的压力系数进行验证。图9 给出了不同输入分辨率时，输入、输出和CFD 标准风压场在2/3 高度处的压力系数，其中，横坐标x表示建筑迎风面2/3 高度处取一条线对应的尺寸。可以看出，分辨率为32 × 32 的风压场重构后的曲线最接近真实值，重构后的值与标准值基本重合；并且输入的分辨率越低，重构后的误差也越大。图10 为某时刻的建筑迎风面2/3 高度处的压力曲线，对比Multi-scale CNN、CNN、Bicubic三种模型的结果可以看出，Multi-scale CNN 模型重构效果明显优于CNN 和Bicubic；但随着输入分辨率越低，三种方法的重构效果均有所降低。

图9 建筑迎风面2/3 高度处的压力系数Fig.9 Pressure coefficient at 2/3 height on the windward face of the building

图10 不同重构方法重构的建筑迎风面2/3 高度处的压力系数Fig.10 Pressure coefficient at 2/3 height on the windward face of building reconstructed by different reconstruction methods

对于不同输入分辨率，Multi-scale CNN、CNN 和Bicubic 重构的建筑迎风面风压场整体误差如表2 所示。可以看出，插值方法的结果误差较大，而深度学习方法能显著提高重构精度；改进的Multi-scale CNN 模型重构精度高于原始的CNN 模型。

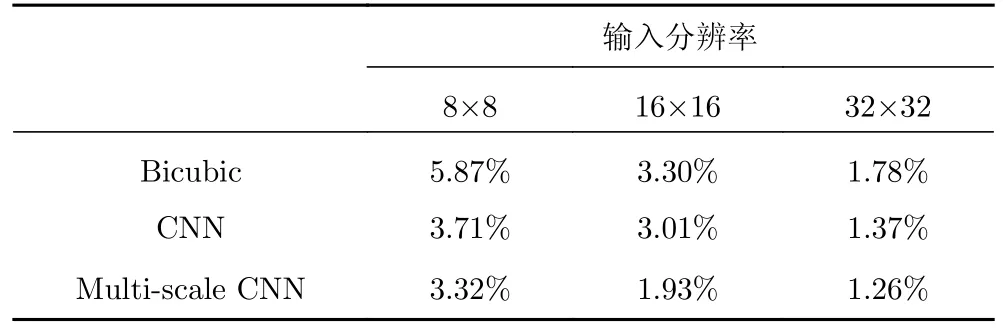
表2 Multi-scale CNN 与CNN、双三次插值重构建筑表面风压场的误差对比Table 2 Error comparison of Multi-scale CNN,CNN and Bicubic interpolation in reconstruction of wind pressure field on building surface

3.2 速度场的超分辨率重构

为了全面评价深度学习模型超分辨率重构的能力，本文对速度场重构效果进行了评估。取120 个xz平面、yz平面、xy平面的x、y、z方向速度场构建数据集。图11、图12 和图13 是输入分辨率为32 ×32 的流场经Multi-scale CNN 模型重构的64 × 64 速度云图，其中，图11 是xz平面过建筑侧面中心的x方向速度云图，图12 是yz平面过建筑迎风面中心的y方向速度云图，图13 是xy平面高于地面0.506 25 m（高于建筑物顶面）的z方向速度云图。由图11～图13可以看出，输入的低分辨率流场经过Multi-scale CNN 模型重构后可以得到精确的流场图像。为了进一步了解速度重构值的精度，在空间取三条直线（位置如图14 所示），对比了三条线上速度的输入值、重构值和标准值，从图15 上可见三条直线上的速度重构值与标准值基本重合，平均绝对误差分别约为1.92%、3.81%和1.88%。

图11 xz 平面x 方向速度云图Fig.11 Velocity contour of x direction of xz plane

图12 yz 平面y 方向速度云图Fig.12 Velocity contour of y direction of yz plane

图13 xy 平面z 方向速度云图Fig.13 Velocity contour of z direction of xy plane

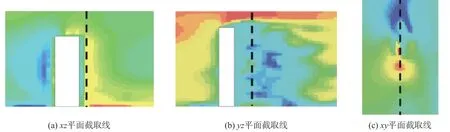
图14 局部直线截取位置示意图Fig.14 Position of local line

图15 局部直线上的速度分布曲线图Fig.15 Curve of velocity distribution on a local line

表3 对比了Multi-scale CNN 模型、CNN 模型和Bicubic 重构对不同低分辨率速度场重构的整体误差。结果显示：三个平面的深度学习超分辨率重构都比Bicubic 重构的误差小；改进后的Multi-scale CNN 精度比原始的CNN 模型有明显的提升，其中精度提高最多的是xz平面中输入分辨率为16 × 16 处，其精度提高了28.24%；输入分辨率越低，重构后的误差越大，但前两种方法重构的误差都要比插值的小。其中xy平面重构的误差都小于其他两个平面，这是由于xz和yz平面过建筑截面，受边界条件影响，深度学习超分辨率重构的过程会有一定的误差。

表3 不同输入分辨率速度场的重构误差对比Table 3 Comparison of reconstruction errors of velocity fields with different input resolutions

4 讨论

上述超分辨重构过程利用来流风向角0°的流场数据集进行训练，获得了超分辨率重构模型，结果显示该模型对来流风向角0°不同瞬时的流场重构具有良好效果。但是当来流条件（如风向角、风速等）发生改变时，训练好的模型参数是否能应用于其他条件下的流场超分辨率重构？

基于以上疑问，本文进一步探索了模型的泛化能力：1）基于来流风向角0°数据集训练得到的模型，重构来流风向角30°的流场（Multi-scale CNN 模型1）；2）在数据集中增加来流风向角30°的流场数据，重新训练超分辨率重构模型（Multi-scale CNN 模型2）。其中，来流风向角30°的流场数据集选取方法同前文来流风向角0°的流场数据集一致，共120 个数据，各样本时间间隔0.005 s。即总的数据集中训练集共有200 个数据，测试集共有40 个数据。

表4 给出了Multi-scale CNN 模型1、Multi-scale CNN 模型2 和双三次插值方法对来流风向角30°的不同输入分辨率风压场和速度场重构的误差。对比可以发现：利用Multi-scale CNN 模型1 训练参数时，最小误差在xz平面、输入分辨率为32 × 32 处，误差大小仅为1.62%，最大误差在建筑表面、输入分辨率为8 × 8 处，误差大小为7.83%；增大数据集后，采用Multi-scale CNN 模型2 重构得到的平均绝对误差总体偏低，最小误差在输入分辨率为32 × 32、xy平面，误差大小仅为0.43%，最大误差在输入分辨率为8 ×8、yz平面，误差大小为4.70%。总体来说，增大数据集后，Multi-scale CNN 模型2 的重构效果最好，误差最小；对于较高输入分辨率流场数据（32 × 32 和16 ×16），双三次插值方法的误差略小于Multi-scale CNN 模型1；对于8 × 8 低分辨率的输入数据，Multiscale CNN 模型1 和双三次插值方法的重构误差均较低，但对于xz平面和yz平面速度场，双三次插值方法的误差略大于Multi-scale CNN 模型1。基于已有模型参数，对不同低分辨率的建筑迎风面风压场进行重构，依旧可以得到高分辨率流场数据，重构后的流场与标准流场基本一致，限于文章篇幅，对比图像不再给出。

表4 三个模型在不同分辨率中重构来流风向角30°流场的误差对比Table 4 Error comparison of Multi-scale CNN 1,Multi-scale CNN 2 and Bicubic interpolation models reconstructed with 30° wind direction under different input resolutions

5 总结

本文将基于深度学习的超分辨率重构方法应用到CAARC 建筑模型绕流流场，采用基于卷积神经网络和混合下采样跳跃连接多尺度(Multi-scale CNN)模型，实现了风向角0°和30°来流条件下的不同空间位置的欠分辨率风压场和速度场的超分辨率重构，可得如下结论：

1）对于输入的不同低分辨率流场数据，基于深度学习的Multi-scale CNN 模型和原始的CNN 模型的超分辨率重构误差均低于传统插值方法的误差；相比原始的CNN，改进的Multi-scale CNN 模型的重构效果有明显的提升。

2）Multi-scale CNN 模型的超分辨率重构效果会受到输入流场的分辨率的影响，输入流场数据分辨率越低，重构高分辨率流场的误差越大。

3）由深度学习模型泛化能力的讨论可得，基于已有流动参数下的流场数据集进行训练得到的Multi-scale CNN 模型参数去重构其他流动条件下的风压场和速度场，可以得到高分辨率流场；在数据集中增加预测流动条件相关的样本，增大数据集，重新训练Multi-scale CNN 模型，可以得到更优的重构效果。

本文的研究结果表明，基于深度学习的超分辨率重构方法可推广应用到具有复杂湍流流动的实际风场中，可对试验或计算数据进行降噪、纠正和丰富数据信息等。后续工作可以考虑不同的超分辨率重构的深度学习模型，如无监督学习方法等，也可在训练过程中加入物理信息约束以提高重构精度。