水平轴风力机偏航与俯仰尾流特性

2024-01-09田尧，高超，刘亚

空气动力学学报 2023年11期

田尧，高超，刘亚

(西北工业大学航空学院,西安 710072)

0 引言

当风吹过风力机时带动叶片旋转，此时叶片对流体的作用导致风力机下游风速减小、湍流度增大、风剪切加剧等流动特征产生，而流体在下游传播一段时间后，在外围流体的作用下，逐渐恢复风速，这种现象被称为风力机的尾流效应[1]。尾流效应产生的风速亏损会使得下游的风力机输出功率降低，并且强湍流和风剪切作用会影响下游风力机的疲劳载荷、结构性能。瑞典航空研究所在风电场的测量结果表明，在风速为12 m/s 的情况下，两台风力机串列相距5 倍叶轮直径时，处于尾流区内的风力机功率输出仅为无干扰时的60%左右，而当相距9.5 倍叶轮直径时，则约为80%[2]。由此可以看出，尾流效应对处于下游的风力机的影响很大，尾流效应的模拟精度直接决定着风电场出力的评估精度，而风电场所能提供的总出力是风电场运营指标的一个重要参数。

针对风力机尾流的数值研究主要有三类：1）计算流体力学（Computational Fluid Dynamics,CFD）；2）尾流数学模型；3）涡方法。CFD可以单独求解风力机上的气动力以及风力机的尾流场，但此种仿真方式所需的计算资源庞大。通常CFD 与叶素动量理论（blade element momentum,BEM）或致动系列算法结合，后者获得风轮后的诱导速度等信息，其结果以体积力源项的形式加入到Navier-Stokes（N-S）方程中，通过CFD 对风力机的尾流场进行求解。Naderi 等[3]采用基于BEM 和CFD的混合方法，利用代表风力机的致动盘模型对尾流的实际形状进行了研究，并研究了不同的湍流模型对尾流形状的影响。通过与现有分析模型的比较表明，由于考虑了湍流的影响，该方法显著降低了用致动盘进行尾流仿真的误差。Gajardo 等[4]针对海上多机组风电平台提出了一种耦合分离涡模拟和BEM 的方法，模拟涡轮阵列来研究尾迹的流体动力学特征及其相互作用，并与实验进行了比较。张建等[5]在气动方面采用致动线与大涡模拟、在结构方面采用柔性多体动力学模型，建立了一种新型双向流固耦合模型，考虑了结构和气动弹性对风力机性能的影响，可用于动态结构载荷预测及流固耦合分析。尾流数学模型是基于一定的实验基础和仿真经验，通过数学模型的形式来描述尾流发展的情况。Brusca 等[6]对Jensen、Larsen 以及Frandsen 尾流模型进行了研究，并通过风洞实验进行了实验验证。在这些模型的基础上，还有人开发出新的解析模型。Tian 等[7]提出并验证了可以估计任意流向位置尾流宽度和最大尾流湍流水平的一维解析模型；在此基础上，提出了一种高效的三维余弦形状模型，可以有效地估算尾流湍流强度。此外，考虑风切变和地面效应，该模型能够描述三维尾流场的各向异性特性。Sun 等[8]提出了一种新型的三维解析型风力机尾流模型，与现有的解析尾流模型相比，Sun 提出的尾流模型考虑了风向在高度方向上的变化，这种变化更加精确，更接近实际情况。Lopez 等[9]等基于不可压RANS 方程，提出了一种针对水平轴风力机偏航状态的尾流模型，该模型能在很短的时间内获得与CFD 相近的仿真结果。涡方法模型从构造风力机叶片表面涡量出发，利用不同程度的涡量分布来模拟叶片与三维流场之间的相互作用。Su 等[10]为了探究风力机偏转产生的尾流倾斜对下游风力机的尾流屏蔽效应是否有积极作用，提出了涡格-等环量轮廓法。Liu 等[11]提出了一种基于BEM 与涡丝法混合的数值尾迹模型，用于预测水平轴风力机尾迹的速度亏损。通过求解风力机下游涡系的演化过程，间接计算了下游速度分布，计算成本非常低。许波峰等[12]建立了一种全自由涡尾迹模型，当线涡从叶片后缘脱落时，其随当地流动速度自由移动；在构建模型时，引入“虚拟周期”的概念，并发展一种自适应松弛因子法，从而改善了自由尾迹迭代的稳定性，提高了迭代收敛速度。曹九发等[13-14]基于非定常自由涡尾迹法和模态法研究了叶片非线性变形对叶片气动特性和尾迹形状产生的影响。周文平等[15]采用Weissinger-L 升力面模型和畸变的自由涡尾迹模型，通过五点中心差分松弛迭代法建立了适用于风力机气动性能计算的仿真模型。通过将自由涡尾迹方法与其他修正模型相结合，可以进一步接近真实物理情况，如三维旋转效应[16]、风切变模型[17-18]等。

为减少风力机尾流干扰效应对下游风力机入流的影响，最有效的解决策略是增大机组间距，但受风场尺寸和地形的影响该策略很难实现，因此对上游风力机采用偏航和俯仰控制以使得尾流的作用区域发生偏转，有效地降低其产生的速度亏损。此外，风力机常年运行在风速与风向随机变化的复杂大气环境中，其中风向的变化可能使得风力机处于偏航或俯仰的工作状态。宗豪华等[19]从无偏航风力机尾流模型、偏航风力机尾流模型、多风力机尾流叠加方法和风电场产能优化四个角度，阐述了主动尾流控制技术；发现在应用主动尾流控制技术后，全尾流干扰风向上的风电场产能可提高约5%～15%，各个风向平均后的年均收益约1%～3%。杨庆山等[20]考虑了偏航控制失效后，风力机在不同停机位置的结构动力响应，同时分析了风力机叶片、塔筒及下部结构响应随偏航角的变化规律及停机位置对响应结果的影响。

针对风力机尾流进行仿真时，使用CFD 可以获得非常精确的结果。然而，在现有计算模型下，CFD需要大量的计算资源和时间，因此难以在工程中广泛应用。相比之下，尾流数学模型计算效率高、耗费资源少，更适合工程应用，但这些尾流模型通常都有很大的局限性，仅适用于较为简单的工况，如无偏航、定常来流等。而升力线自由涡尾迹方法较尾流数学模型更加接近真实物理情况，同时较CFD 方法具有更高的计算效率，可以在一定程度上实现计算精度和计算效率之间的平衡。

本文基于升力线模型和自由涡尾迹模型建立了风力机气动仿真模型，以Nibe 风力机为基准算例验证了模型对尾流仿真的可行性和准确性。同时以NREL 5MW 风力机为研究对象，探究了不同风速下风力机偏航/俯仰状态下的尾流结构，对尾流结构、失稳特性进行了深入分析。为了研究风力机在风电场中工作时的真实尾流状态，考察了风切变和塔架对风力机偏航和俯仰工况时尾流的干扰作用。

1 数值模型

1.1 升力线自由涡尾迹模型

升力线自由涡尾迹模型（lifting line-free vortex wake,LLFVW）是由升力线模型和自由涡尾迹模型构成，如图1 所示。升力线模型是将风力机的叶片以一根强度沿着展向变化的线涡来代替，从而表征来流与风力机叶片的相互作用，该线涡称为附着涡。根据Helmholtz 第二定律可知，在无黏环境下，涡不能在流场中终止，只能延伸到流场边界或构成环，因此附着涡沿展向的变化量会形成尾流涡。同时，在非定常来流条件下，附着涡随时间的变化量也会脱落至尾流中，形成脱落涡。

图1 升力线自由涡尾迹模型Fig.1 Lift line model

基于不可压缩的三维假设，用来描述涡量场的N-S 方程为：

式中：ω为涡量，V为涡元速度，∇为哈密顿算子，υ为动力学黏性系数。方程的右侧依次是对流项、拉伸项和扩散项。

有研究表明[21]，相比势流流动，黏性作用局限于更小的长度尺度。因此采用基于拉格朗日描述法的自由涡尾迹模型对尾流场中的线涡运动进行描述。在无旋不可压假设下，描述这些离散涡丝运动的控制方程可简化为简单的对流方程:

式中：r为涡元节点的位置矢量，r0为初始位置，V(r,t)为r处流体的速度矢量。方程（2）看似简单，但由于局部流体速度V(r,t)具有较强的非线性特性，需要进一步处理才能保证方程求解的鲁棒性。

如图2 所示，根据风力机尾流特性，方程（2）可以通过风力机叶片的方位角和尾流的寿命角进行离散：

图2 叶尖涡离散示意图Fig.2 Schematic of tip vortex dispersion

式中：ψ为叶片方位角，ζ为尾流寿命角。叶片方位角和尾流寿命角对时间的导数都是叶轮转速Ω，根据链式法则，式（3）可以转化为：

对于偏微分方程（4）采用有限差分法进行数值求解，方程（4）的左边是一维尾迹方程。对于叶片方位角的离散采用由Bagai 和Leishiman[22]提出的五点中心差分方法（PCC）进行离散。如图3 所示，该方法通过网格中点附近的值来计算 ψ 和 ζ在网格中点的导数。方程（4）左侧的方位角导数差分形式可转化为：

图3 PCC 差分方法Fig.3 Schematic of PCC difference method

对于尾流寿命角的离散采用Bhagwat 和Leishman[23]提出的二阶后向差分算法（PC2B）。如图4 所示，该方法使用前三个时间步的信息来进行当前时间步的有限差分近似计算。方程（4）左侧的寿命角导数差分形式可转化为：

图4 PC2B 差分方法Fig.4 Schematic of PC2B difference method

方程（4）右侧的速度包括来流速度、尾流场中涡诱导速度以及旋转速度：

诱导速度通过Biot-Savart 定理求解，其离散形式表示为：

式中：Γ为涡元强度，r1和r2表示当前离散涡丝的两个端点到目标点P 的矢量。

当目标点P 在涡丝上或无限接近涡丝，诱导速度趋于无穷大，显然不符合物理实际。为消除这一奇性，引入Vatistas 涡核模型作为诱导速度计算式系数：

式中：h为目标点到涡丝的垂直距离；n是一个经验参数，取不同的值代表不同的经验模型，本文的仿真均采用n=2；rc为瞬时涡核半径，其有经验公式：

式中：k为经验参数，其值为1.254 6；t为时间。

1.2 三维效应修正

采用升力线模型来代替叶片对于入流风的作用需要利用叶片截面翼型的实验升阻力参数，虽然不需要再去考虑黏性的作用，但是需要对旋转带来的三维效应作进一步处理。在叶片旋转过程中，主要是离心力和科氏力会带来三维效应，离心力会使得叶片表面产生径向的流动，科氏力会使得叶片逆压梯度减小，推迟表面流动分离。目前常用的三维旋转修正模型多采用基于实验的半经验模型，本文选取Du-Selig 修正模型[24]来修正升阻力系数，其形式如下：

式中：CL,p=2π(α-α0)，其中α是当前迎角，α0是零升迎角；CD,0是迎角为0°时的二维阻力系数CD,2D。升阻力修正系数为：

其中：

式中：c是当前翼型的弦长；r是当前叶元的半径，也即当前叶元的径向距离；R是叶片半径；a、b、d、Λ均为经验参数。

1.3 叶尖损失修正

风力机叶片在真实流场中工作时，由于吸力面和压力面存在压差，因此会有从压力面到吸力面的绕流运动，此时叶尖的升力应为0。但是升力线方法直接采用二位翼型的气动特性曲线，在迎角不为0°的情况下，由升力线获得的叶尖升力不为0，这与真实情况相矛盾，因此需要对叶尖的二维升阻力系数进行修正。

多数叶尖损失修正模型需要计算叶元的诱导系数，但采用升力线自由涡尾迹方法时，诱导系数计算复杂，因此本文采用可以直接对二维翼型升阻力系数修正的Shen 模型[25]，其格式如下：

式中：ΦR为当前截面处相对风速和叶轮平面的夹角；g是经验参数，其值如下：

式中，c1、c2均为经验参数，分别取值0.125、21；λ为叶尖速比。

1.4 风切变和塔影模型

风切变模型是指风速大小和方向在空间上的变化，针对风力机通常采用指数模型来描述风速在竖直方向上的变化：

式中，V(z) 为高度z处的风速，Vhub为轮毂高度的风速，zhub为轮毂高度，γ为风切变系数，本文中取值0.2。

针对涡丝的离散中采用了叶片的方位角，为了方便计算，在计算叶片上的风速时，针对式（24）中的z也采用方位角和叶片的径向距离进行描述：

式中θ是叶片的方位角。

塔影模型是描述风速受塔架干扰、塔架正前方风速减小、两侧气流加速的模型。本文采用Powles[26]塔影模型，其表达式如下：

2 模型验证

本文以丹麦Nibe 风力机[27]作为数值模型的验证算例，其主要参数如表1 所示。

表1 Nibe 风力机特性Table 1 Nibe turbine characteristics

图5 为Nibe 风力机在轴向上不同位置处的速度剖面图，以实验结果为基准，对比了LLFVW 模型和Jensen 模型以及修正的2D_Jensen 模型[28]的结果。从图中可以看出风力机尾流速度在轮毂中间位置存在速度最低点，并且随着轴向位置的增加，风力机尾流速度不断恢复。在近尾流区，LLFVW 模型获得速度分布与实验值趋势相同，并且能够获得速度亏损最大值，而Jensen 模型低估了速度亏损，2D_Jensen 模型高估了速度亏损。在远尾流区，Jensen 模型能够获得速度亏损的最大值，但其速度分布与实际尾流结果相差较大，而2D_Jensen 模型仍然高估了远尾流区的速度亏损，相比之下LLFVW 模型能得到与实验结果接近的速度亏损分布情况。因此，采用LLFVW 模型不仅具有较高的计算效率，而且具有良好的计算精度。

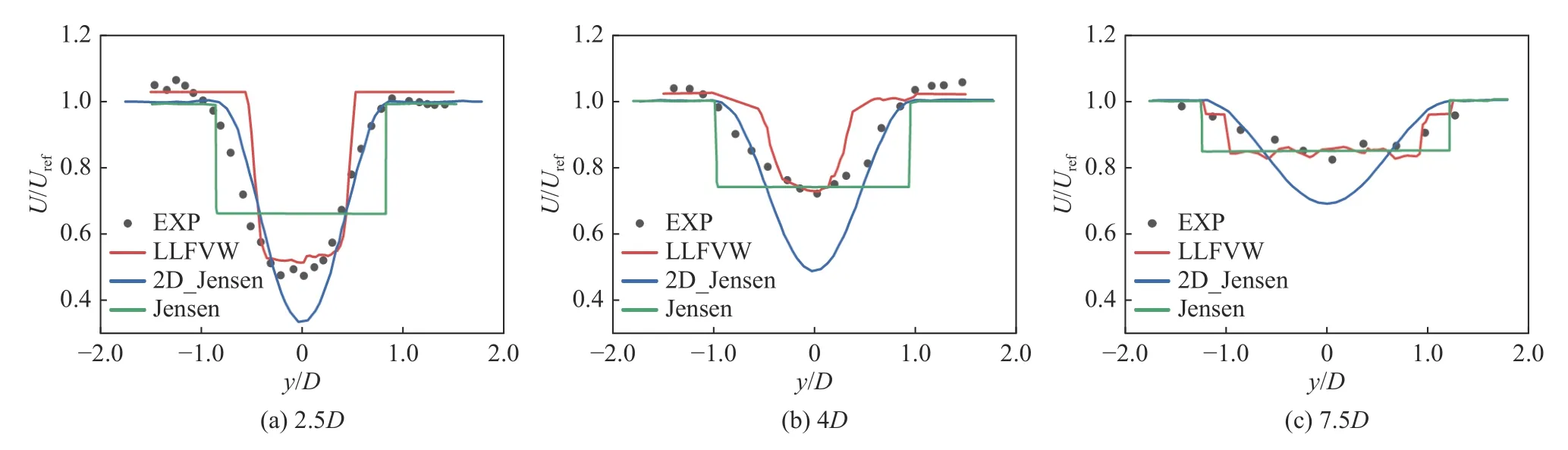
图5 Nibe 风力机下游不同位置处速度剖面对比图Fig.5 Comparison of downstream velocity profiles bewtween different locations of the Nibe wind turbine wake

3 NREL 5MW 偏航和俯仰仿真

本文以NREL 5MW 风力机[29]为研究对象，其详细参数如表2。

表2 NREL 5MW 风力机特性Table 2 NREL 5MW turbine characteristics

3.1 气动特性验证

图6 给出了不同风速下计算获得的风轮气动功率和推力结果，并以近年来不同CFD 方法[30-33]的仿真结果作为对比。NREL 开发的FAST 程序包含BEM 模块，并且为了提高BEM 的计算精度加入了各种修正模型。虽然仍不能获得风机尾流场的流动特性，但在计算上游风机的气动特性时，可获得精度可接受的结果。从图中可以看出，采用LLFVW 模型获得的气动功率和推力与其他仿真模型的结果变化规律相同，各个风速下都能获得与CFD结果接近的值。推力结果显示，当风速大于13 m/s 时，CFD 获得的结果小于升力线自由涡尾迹方法。由于上述研究人员采用了不同的结构仿真模块、考虑了叶片变形的结果，因此在高速来流情况下，叶片变形改变了风轮的扫掠面积，降低了转子的整体推力；并且在风速高于额定风速时，需要采用变桨控制等方式实现功率的稳定。各种仿真手段采用不同的控制策略也可能导致高速来流条件下气动结果的差异。

图6 不同风速下的气动特性Fig.6 Aerodynamic characteristics at different wind speeds

3.2 不同偏航角尾流特性

在风电场中，上游风力机与来流相互作用会产生螺旋状的涡尾迹，这种尾流结构会导致下游风速减小、湍流度增大、风剪切加剧，从而降低下游风力机的产出。对于大型风电场而言，由尾流干扰所引起的产能损失最高可达30%～40%。为了减少尾流干扰所带来的不利影响，常见的尾流控制方法有静态偏航控制、周期性变桨距、风轮仰角控制等[34]。其中，静态偏航控制工程实现难度较低，尾流偏转效率较高，同时可避免叶片动载荷的增大[35]。因此，本文针对NREL 5MW 风力机研究了不同偏航角工况下的尾流特性。

图7 给出了NREL 5MW 风力机在偏航角βyaw=0°～30°的尾流结构。从图中可以看出附着涡脱离叶片后形成的尾流涡和脱落涡在近尾流区能保持稳定的涡结构，随着与外围流体的相互作用，稳定的涡结构被破坏，尾流场中湍流度增大，尾流区内的速度逐渐恢复。同时，随着偏航角的增大，涡结构的失稳更早发生，且相同位置的远尾流区湍流度更大。

图7 不同偏航角尾流涡结构Fig.7 Wake vortex structure at different yaw angles

图8 是轮毂高度处额定风速11m/s、βyaw=0°～30°的尾流速度分布。相比轴流风力机尾流，在偏航诱导产生的非零侧向力和展向速度作用下，风力机的尾流中心线随着流动向下游传播而发生偏移，且偏航角度越大偏移越明显。由于尾流的扩张效应，偏航产生的展向速度沿流向会逐渐减小，偏航角30°时风力机尾流在下游8D处后的中心线偏转量基本保持0.5D不变。除了改变尾流方向外，偏航降低了尾流干扰对下游的影响，尾流作用区域随着偏航角的增大而减小，同时在尾流作用区域内，偏航角越大速度亏损越小。

图8 不同偏航角轮毂高度处速度云图Fig.8 Velocity contours of hub height at different yaw angles

图9 给出了偏航条件下的速度云图。偏航风力机的尾流速度剖面与轴流风力机尾流明显不同，表现为上下不对称的“肾”形。结合尾流涡结构的发展，分析认为导致该尾流结构产生的原因是轮毂涡和叶尖涡的流向涡量相互诱导融合，形成一个对转涡包，该涡包诱导产生横向速度，横向速度的运输导致了非对称“肾”形尾流速度剖面。

图9 偏航条件下不同尾流位置处速度剖面Fig.9 Velocity profiles at different wake positions under yawed conditions

图10 是风轮下游不同位置轮毂高度处的速度型。在1D处，各个偏航角的尾流速度分布呈“高帽”形，偏航导致的尾流中心线偏转现象并不明显，但中心线左右速度亏损不对称，偏转侧的作用区域更小。随着流动向下游发展，偏航尾流的中心偏转明显，在外围流体的作用下，速度亏损恢复较快。3D处涡结构开始失稳，其诱导产生的速度使得尾流速度分布不再规律，各偏转状态的风力机尾流不再保持对称结构。

图10 偏航条件下不同位置处轮毂高度速度型Fig.10 Hub height velocity at different positions under yaw conditions

3.3 不同俯仰角尾流特性

风轮的俯仰可以改变风力机尾流在竖直方向的分布，使得尾流发生竖直偏转，从而达到控制尾流干扰效应的目的。图11 给出了NREL 5MW 风力机在俯仰角βtilt=0°～30°下的尾流结构，从图中可以看出，与偏航情况类似，随着俯仰角的增大，涡结构的失稳更早发生，且相同位置的远尾流区湍流度更大。

图11 不同俯仰角尾流涡结构Fig.11 Wake vortex structure at different tilt angles

图12 是额定风速11 m/s、俯仰角0°～30°、风力机中心截面的尾流速度分布。俯仰会使得尾流中心线发生偏移，同时也存在一个偏移极限。在尾流作用区域内，尾流作用半径减小，速度亏损减弱。

图12 不同俯仰角风轮中心截面速度云图Fig.12 Velocity contours of turbine center section at different tilt angles

图13 给出了风轮俯仰情况下不同下游位置的速度云图。从图中可以看出，与偏航类似，俯仰也会导致尾流速度剖面呈水平不对称“肾”形结构；并且俯仰角的风轮会对来流产生抬升作用，使得尾流作用区域上升，作用区域减小。目前在部分陆上风电场中，风电机组布局在竖直方向存在高度差，采用风轮俯仰控制可以使上游风力机的尾流发生竖直方向的偏转，有效降低上游风力机尾流对下游风力机入流的干扰，实现尾流干扰的控制。

图13 俯仰条件下不同尾流位置处速度剖面Fig.13 Velocity profiles at different wake positions under tilted conditions

图14 是俯仰条件下不同位置处轮毂高度速度分布。与偏航不同的是，在下游1D位置处俯仰工况的尾流速度亏损基本保持对称结构。随着流动向下游发展，俯仰工况的尾流作用区域上移，轮毂高度的尾流亏损小于轴流工况的结果。在4D位置处时，与轴流工况相比，俯仰角30°时速度亏损显著恢复。

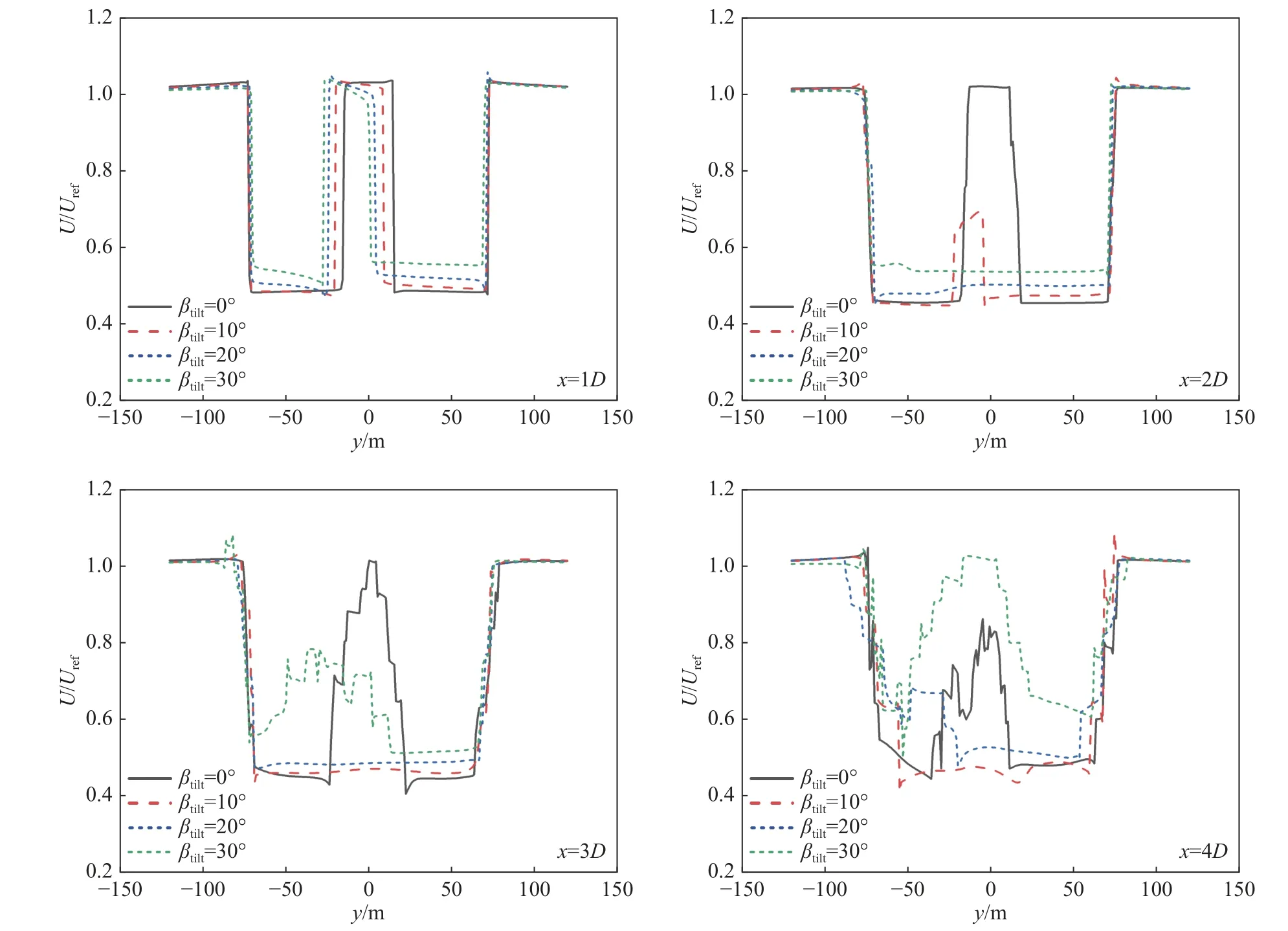
图14 俯仰条件下不同尾流位置处轮毂高度速度型Fig.14 Hub height velocity at different wake positions under tilt condition

3.4 考虑风切变/塔架的尾流特性

风力机在实际运行过程中，风切变和塔架是非常典型的干扰因素，两者都会导致风力机气动功率发生波动和损失，同时也会改变风力机的尾流结构，使其发生畸变，而这种畸变会反作用于风轮平面，进一步影响风力机叶片的气动性能。因此探究风切变和塔架干扰条件下风力机偏航和俯仰的尾流意义重大。

图15 是考虑风切变和塔架后风力机偏航角0°～30°的轮毂高度速度云图。从图中可以看出，在考虑风切变和塔架后，轴流工况的尾流作用区域不再保持对称结构，且作用区域显著减少。同时在考虑两种干扰条件下，偏航仍可以减小上游风力机的尾流效应对下游区域的影响，在尾流作用区域内速度亏损更小。

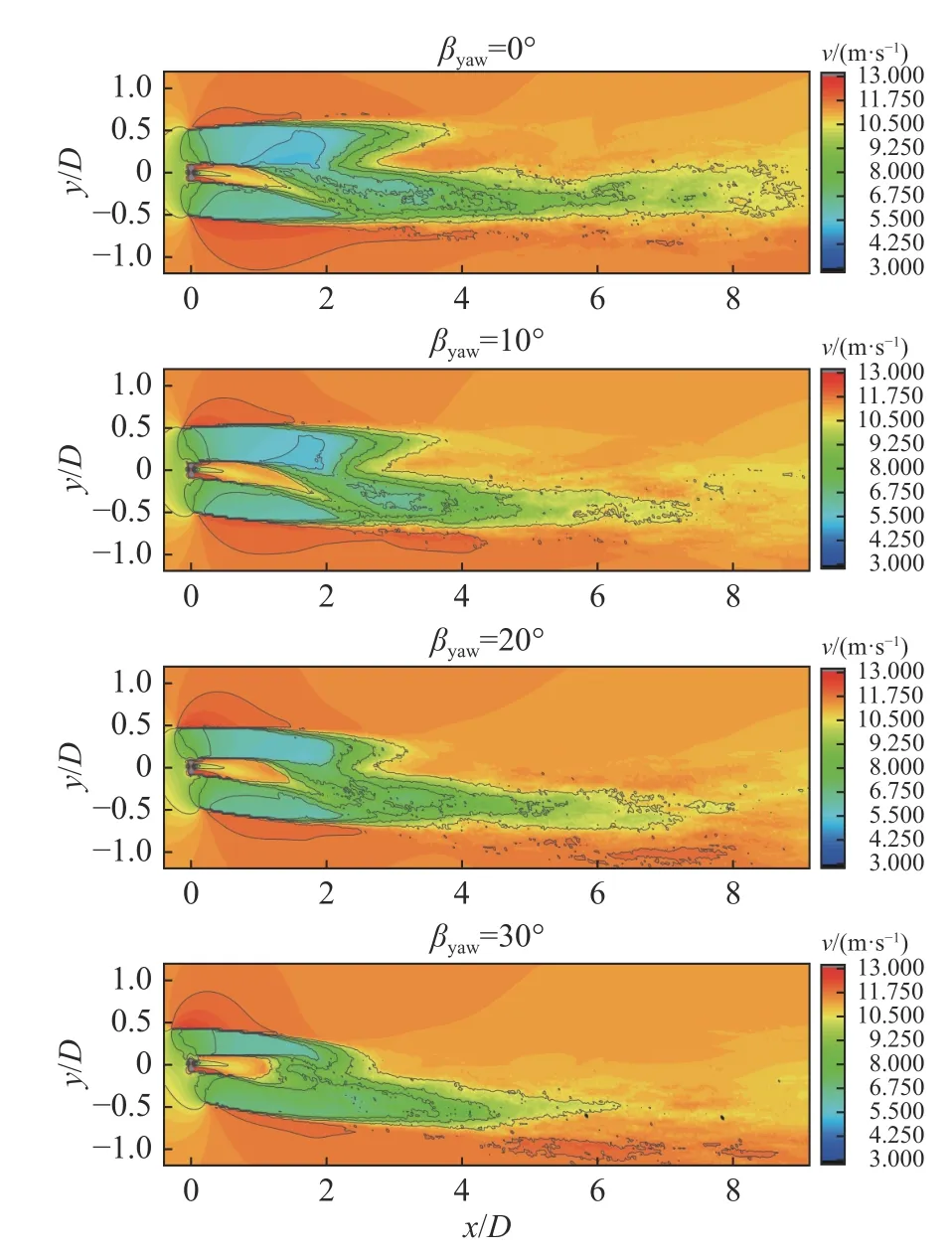
图15 风切变和塔架干扰下不同偏航角的轮毂高度速度云图Fig.15 Hub height velocity contours at different yaw angles under wind shear and tower interference

图16 是考虑风切变和塔架后，偏航工况不同下游位置截面的速度云图。从图中可以看出风切变模型会产生类似风轮俯仰的效果，使得风力机的尾流中心在竖直方向发生偏转，同时在偏航的作用下，尾流中心发生水平方向的偏转。由于塔架的作用，在近尾流区下半部分的风速低于上半部分，但在2D位置之后塔架作用效果减弱。

图16 风切变和塔架干扰下不同偏航角下游位置速度剖面Fig.16 Velocity profiles of downstream positions at different yaw angles under wind shear and tower interference

图17 给出了考虑风切变和塔架后风力机俯仰0°～30°的风力机中心截面速度云图。当俯仰角为0°时，直观地反映了风切变对尾流的抬升作用，且速度亏损恢复加快。塔架对尾流的显著干扰效果在3D处之前较为明显，而俯仰会降低塔架对近尾流区的干扰作用。

图17 风切变和塔架干扰下不同俯仰角的风轮中心截面速度云图Fig.17 Turbine center section velocity contours at different yaw angles under wind shear and tower interference

图18 是考虑风切变和塔架时，俯仰工况不同下游位置截面的速度云图。从图中可以看出，相比理想状态，风切变和塔架的作用会进一步提高风力机俯仰对尾流干扰的控制效果，加快速度亏损恢复。在风力机未俯仰时，塔架对近尾流区下半部分扰动明显，随着俯仰角的增大，干扰效果逐渐降低。

图18 风切变和塔架干扰下不同俯仰角下游位置速度剖面Fig.18 Velocity profiles of downstream positions at different tilt angles under wind shear and tower interference

图19 给出了额定风速11.4 m/s 下，各个控制策略的功率随角度的变化。从图中可以看出，在不考虑风切变和塔架影响时，风力机气动功率随偏航或俯仰的角度增大而近似呈线性减小；相较轴流工况，偏转30°时两种控制方式的功率降低约18%。在相同偏转角度下，俯仰导致的功率降低小于偏航的结果，在偏转30°时，俯仰较偏航功率高2%。考虑风切变和塔架影响时，气动功率随偏航或俯仰角度的增大呈非线性降低，偏转角度较小时，功率降低小；但在偏转30°时，偏航的功率降低约20%，俯仰的功率降低约19%。偏航和俯仰在相同偏转角度下的气动功率差值更大，在偏转30°时两者的气动功率相差3.8%。