考虑风切变影响的三维尾流模型风场实验

张绍海，高晓霞，*，朱霄珣，王 瑜，王 喜

(1.华北电力大学 动力工程系，保定 071003；2.河北省低碳高效发电技术重点实验室，保定 071003；3.保定市低碳高效发电技术重点实验室，保定 071003；4.华北电力大学 电子与通信工程系，保定 071000；5.河北龙源风力发电有限公司，张家口 076450)

0 引言

尾流效应是指自然风在流经上游风力机组之后，部分风能转化为机械能，导致风速降低、湍流程度增加的现象[1-2]，其会导致下游风力机发电量降低，疲劳载荷增加，进而影响风力机的安全运行[3]。尾流在风力机下游会传播很长一段距离才能逐渐恢复到自由流水平，因此一台风力机可能会受到多个上游风力机的尾流影响。尾流效应评估不当将会导致发电量评估不准确，如高估发电量将对电气设备电压等级和电缆容量提出过高要求，影响整个风电场的运行储备和控制策略，这最终会导致对组件的投资浪费[4]。

针对风力机尾流场的研究方法主要有数值模拟、建立尾流模型、风洞实验及风场实验[5]。吴正人等[6]通过数值模拟研究了不同层结状态下风力机尾流对大气参数的影响；薛飞飞等[7]基于格子玻尔兹曼方法和大涡模拟方法研究了风力机尾流；曹九发等[8]采用LES 耦合致动线模型方法分析了多台风力机尾流变化。数值模拟虽然具有很高的精度，但是其高昂的计算成本限制了其在工程应用中的发展，而工程尾流模型却较好地克服了这一缺点。人们提出了一系列针对远尾流区域的工程尾流模型以评估风电场微观选址中风力机尾流效应引起的功率损失，如Jensen[9]、Bastankhah 和 Porte-Agel[10]、Frandsen[11]、Tian[12]、Gao 等[13]以及赵飞等的模型[2]。在实际的风电场中，由于地面资源有限，很多风力机的间距都小于5 倍风力机直径[14]，而近尾流区域一般小于3～5 倍风力机直径[15]，很多风力机都会受到近尾流的影响，所以非常有必要对近尾流区域进行研究。利用质量和动量守恒，Blondel 等[14]提出了一种基于超高斯函数的二维全尾流模型，该模型在近尾流区域为超高斯形，在远尾流区域为高斯形。Keane 等[16-17]和Schreiber等[18]提出了基于质量和动量守恒的双高斯速度亏损分布模型。上述的全尾流模型虽然符合近尾流和远尾流的水平分布特征，在水平剖面上具有良好的精度，但并没有考虑风切变的影响，无法准确描述尾流在垂直剖面上的分布特征，对尾流空间分布特征的描述还不完善。

风洞实验和风场实验是尾流模型验证的两种主要方法[19]。风洞实验的优点是可以控制风速、风向以及湍流强度等实验条件，方便学者在特定的风况下观察尾流现象；但也存在一些限制，如大气边界层不能在风洞中完全模拟、采用的风力机模型并不能达到真实风力机的雷诺数值以及阻塞率的影响等[20-22]。目前，利用激光雷达进行风场实验很受学者们欢迎，因为其很好地弥补了风洞实验的不足，高精度的激光雷达可以捕捉到大范围的三维尾流分布特征，且测量的尾流数据更符合实际[13]。

鉴于以上分析，本文提出了一种基于双高斯函数的三维尾流模型，该尾流模型通过旋转修正的方式引入了风切变的影响，并考虑了近尾流区域的变化特征，能够较为准确地描述整个尾流区域的三维空间分布，提高下游风力机的功率评估精度。同时，在河北石人风电场进行了风场实验，使用两台陆基激光雷达测量了风场的自由流和尾流信息，利用实测的风场数据验证了新提出的三维尾流模型的有效性。

1 三维尾流模型的推导

以风力机轮毂中心为坐标原点，风力机尾流中心线为x轴，垂直于尾流中心线且竖直向上为z轴，垂直于尾流中心线且水平向右为y轴。

1.1 Jensen 模型

Jensen 模型是典型的一维尾流模型，其表达式简单，计算效率高，被许多学者用来作为推导尾流模型的基础，其表达式如下：

式中：uhub为在轮毂高度处测量的入流风速；k为Jensen 尾流膨胀系数，在陆上风电场k=0.075[9,23]；r0为初始尾流半径；rx为尾流半径；a为轴向诱导因子；D为风力机的直径；CT表示推力系数。

1.2 风切变模型

在实际的风场环境中，由于地面摩擦的影响，风速会随着垂直高度的增加而增加，其风廓线类似于指数形式，所以本文采用了以下风切变模型：

式中，α为自由流风切变指数，由风场测量的自由流风廓线拟合得到。注意，该风切变模型以轮毂中心为坐标原点，其绝对高度为z+zhub。

1.3 双高斯函数

双高斯函数可以从单高斯形平滑地过渡到双高斯形，这和以往实验观测到的尾流剖面形状相吻合[17,24]，所以本文采用双高斯函数作为基础来推导三维尾流模型，其表达式如下：

式中，xmin为高斯极小值到函数中心的距离。当xmin=0，为单高斯函数；当xmin≠0，为双高斯函数。

1.4 垂直平面的简化模型（不考虑风切变）

在忽略风切变影响的情况下，尾流风速是呈对称分布，所以本文假设未考虑风切变影响下的尾流风速u(x,z)为对称双高斯分布，其表达式如下：

式中，zmin为从高斯极小值到转子中心的垂直距离，A为待确定的未知参数，σz为垂直方向上的特征宽度。

由Jensen 模型可得尾流区域的流量通量，本文假设新提出的三维尾流模型和Jensen 尾流模型的流量通量相同，所以可得式（5）：

由式（5）解得参数A为：

得到的垂直平面的简化模型为：

式中rz为垂直方向上的尾流半径。

1.5 旋转修正

式（7）忽略了垂直方向上风切变的影响，认为垂直方向上的自由流风速为常数，但是这并不符合实际，所以下一步将对式（7）进行修正。有研究表明，以轮毂中心高度为风速中心点，自由流风廓线近似为一次函数形式[2]。考虑到由于风切变的影响，尾流的垂直剖面为非对称分布，且自由流风廓线近似为一次函数形式，所以可采取旋转修正的方法对式（7）进行修正。

以坐标原点为旋转点顺时针旋转角度 β∗后的尾流速度及垂直高度为（横轴为尾流速度，纵轴为垂直高度）：

值得注意的是，在进行旋转修正时，是由垂线（垂直方向上的风速相同）旋转为斜线，如图1 所示。所以以尾流中心线为旋转中线旋转角度 β后的修正尾流速度表达式可化解为下式：

图1 旋转修正示意图Fig.1 Schematic of rotation correction

式中，旋转角度 β由风场实验测量的来流风廓线拟合得到。联立式（7～9）可得垂直平面考虑风切变的尾流速度表达式如下：

1.6 水平面的尾流模型

由于水平方向上并不存在风切变的影响，所以水平面与垂直方向未考虑风切变的尾流模型类似，也为对称双高斯形，其表达式如下：

式中，ymin为从高斯极小值到转子中心的水平距离；σy为水平方向上的特征宽度；ry为水平方向上的尾流半径。

1.7 高斯极小值到转子中心距离和特征尾流宽度

本文采用文献[24]中提出的高斯极小值到转子中心距离及特征尾流宽度的表达式，如式（12）所示：

式中，kz为垂直方向上的尾流膨胀系数，ky为水平方向上的尾流膨胀系数。

由于水平方向和垂直方向的尾流膨胀速度并不相同，所以本文采用了He 等[25]推导的具有各向异性的尾流膨胀系数表达式，如式（13）所示：

2 风场实验

实验在河北省张家口的石人风电场进行，该风电场现役的风力机主要为联合动力公司的UP77 型号风力机。图2 给出了UP77 型号风力机的推力系数曲线和功率曲线，UP77 的具体参数规格见表1。

表1 UP77 风力机的参数规格Table 1 Parameters and specifications of UP77 wind turbine

图2 UP77 型号风力机的功率曲线和推力系数曲线Fig.2 Power curve and thrust coefficient curve of UP77 wind turbine

实验使用了两台地基式扫描激光雷达进行测量，型号分别为Wind3D 6 000（W3D6000）和WindMast WP350（WP350）。W3D6000 用于测量风力机尾流的三维分布特征，有PPI 和RHI 两种扫描模式。PPI 模式（固定仰角，改变方位角）用于测量尾流的水平剖面尾流速度，而RHI 模式（固定方位角，改变仰角）用于测量垂直剖面尾流速度，PPI 模式和RHI 模式设置的参数见表2。WP350 用于捕获自由流风速信息，如自由流的风剖面以及湍流强度等。

表2 W3D6000 的PPI 模式和RHI 模式设置参数Table 2 PPI mode and RHI mode setting parameters of W3D6000

根据测风塔测量的风速信息确定该风电场的主风向为西北方向，所以将WP350 放置在10-2 风力机的西北方向（WP350 与10-2 风力机相距160 m），将W3D6000 放置在了10-2 风力机的东南方向（W3D6000 与10-2 风力机相距1 275 m），如图3 所示。这样布置激光雷达可尽量减少风向变化对尾流的影响，可测量到更为完整的尾流剖面。

图3 风场实验的仪器布置Fig.3 Instrument arrangement of wind field experiment

3 三维尾流模型的验证

3.1 水平剖面（z=0）验证

图4 是在3 月27 日测得的风电场风力机尾流水平剖面云图，从云图可看出10-3 风力机的尾流较为完整，所以本文以10-3 风力机作为观测目标以验证尾流模型对水平剖面预测的有效性。

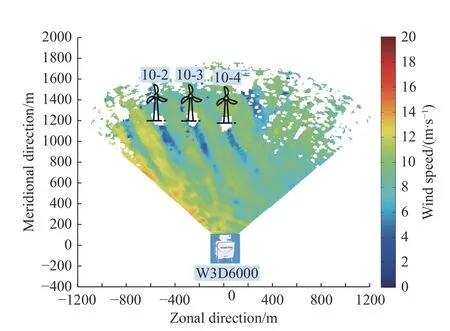
图4 W3D6000 测量的风力机尾流水平剖面云图Fig.4 Horizontal profile cloud diagram of wind turbine wake measured by W3D6000

图5 为WP350 测得的该风场的3 月风玫瑰图。由WP350 测量的10 min 内的自由流平均湍流强度I0=0.11，自由流风速uhub=9.38 m/s，对应的推力系数CT=0.725（由图2 查得）。

图5 WP350 测量的3 月风玫瑰图Fig.5 Wind rose in March measured by WP350

图6 是下游6 个位置（包括了近尾流和远尾流）的实验数据和本文三维尾流模型预测曲线的水平剖面对比结果，横轴为水平坐标与风力机直径的无量纲比，纵轴为尾流速度和轮毂中心自由流风速的无量纲比。从实验测得数据分布来看，在近尾流范围内，水平剖面近似于对称双高斯形，而到了较远的尾流段，其分布类似于单高斯形。从总体的比较结果可以看出，不管是在近尾流还是在远尾流，三维尾流模型与实验数据都拟合良好。

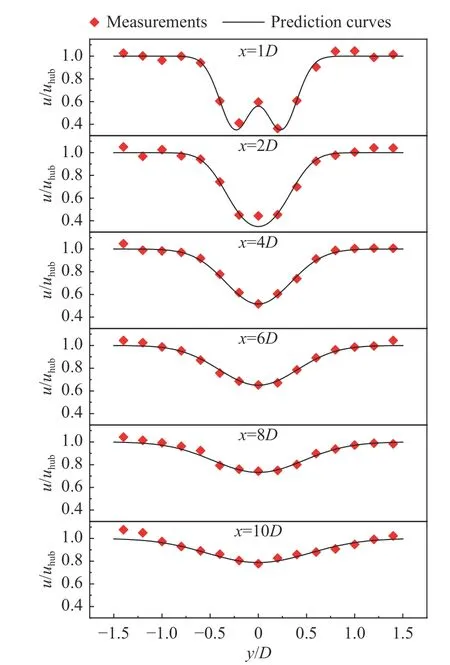
图6 三维尾流模型预测的下游6 个位置水平剖面与实测数据的对比Fig.6 Comparison between horizontal profiles at 6 downstream locations predicted by the three-dimensional wake model and measured data

图7 为尾流模型预测的水平剖面的相对误差分析。在下游x=1D处，本文三维尾流模型预测的最大相对误差在y=-0.2D处，为-12.84%，平均相对误差为2.94%；在下游x=2D处，三维尾流模型预测的最大相对误差在y=0处，为-21.34%，平均相对误差为3.81%；在远尾流区域（x=4D，x=6D，x=8D，x=10D），三维尾流模型预测的最大相对误差为-7.83%，其预测效果比近尾流的两个位置要好。

图7 层流模型预测的水平剖面的相对误差分析Fig.7 Relative errors analysis of horizontal profiles predicted by laminar flow model

从相对误差分析结果可看出，新提出的三维尾流模型在下游x=2D处的预测误差最大。这可能是由于x=2D处位于近尾流和远尾流的过渡区，而过渡区的尾流分布特征处于近尾流和远尾流之间，所以三维尾流模型在x=2D处的预测误差比其他几个下游位置的预测误差大。

3.2 垂直剖面（y=0）验证

图8 是1 月6 日W3D6000 测量的10-2 风力机的垂直剖面层流云图，该图以W3D6000 为坐标原点，经度方向为x轴，垂直方向为y轴，10-2 风力机的轮毂中心坐标为（1 275，137）。

图8 W3D6000 测量的垂直剖面层流云图Fig.8 Cloud diagram of vertical profile laminar measured by W3D6000

图9 是WP350 测量的该风场的1 月风玫瑰图。由WP350 测量的自由流10 min 内的平均湍流强度I0=0.1，自由流风速uhub=9.25 m/s，对应的推力系数CT=0.733（由图2 得到）。

图9 WP350 测量的1 月风玫瑰图Fig.9 Wind rose in January measured by WP350

图10 为WP350 测量的自由流风廓线，其拟合的风切变指数α=0.25，对应的修正旋转角度 β=16◦。注意，由于本文的验证均采用的是无量纲参数，所以对应的修正旋转角度 β为无量纲参数下的旋转角度。

图10 WP350 测量的来流风廓线Fig.10 Incoming wind profile measured by WP350

为了验证本文三维尾流模型对垂直剖面预测的有效性，选取10-2 风力机6 个下游位置（包括近尾流和远尾流）进行验证。图11 是本文三维尾流模型预测曲线和实验数据以及未修正的三维尾流模型预测曲线的垂直剖面对比结果，横轴为尾流速度和轮毂中心自由流风速的无量纲比，纵轴为垂直坐标与风力机直径的无量纲比。从实验测得数据分布来看，在近尾流范围内，水平剖面近似于非对称双高斯形，而到了较远的尾流段，其分布类似于非对称单高斯形。从总体比较结果可以看出，不管是在近尾流还是在远尾流，本文三维尾流模型与实验数据都拟合良好，而未修正的尾流模型由于没有考虑到垂直方向上的风切变影响，所以其预测误差较大，特别是在远尾流区域。

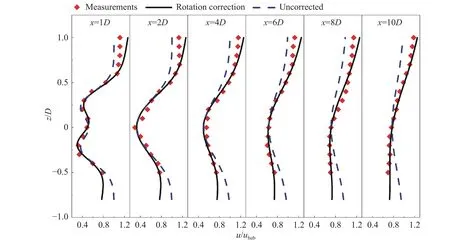
图11 三维尾流模型和未修正尾流模型的预测曲线和实验数据的比较结果Fig.11 Comparison of prediction curves and experimental data of three-dimensional wake model and uncorrected wake model

为了进一步对垂直剖面的预测结果进行分析，本文对垂直剖面的相对误差进行了分析，如图12 所示。在下游x=1D处，三维尾流模型预测的最大相对误差在z=-0.2D处，为-16.95%，平均相对误差为7.69%；在下游x=2D处，三维尾流模型预测的最大相对误差在z=0.1D处，为-20.06%，平均相对误差为7.04%；在远尾流区域（x=4D，x=6D，x=8D，x=10D），三维尾流模型预测的最大相对误差为-12.39%。从相对误差分析结果可看出，本文三维尾流模型对于近尾流的预测精度要低于远尾流，且最大误差出现在尾流中心线附近。这可能是由于近尾流区域存在叶尖涡的影响，并且在近尾流区风力机轮毂对中心线上的尾流也会存在干扰，导致近尾流区的湍流强度变化要比远尾流区域的复杂；而本文尾流模型只是采用了一个经验参数表达式，其很难准确预测近尾流区域的复杂湍流强度变化，所以对近尾流区域的中心线上的尾流预测精度要稍差。

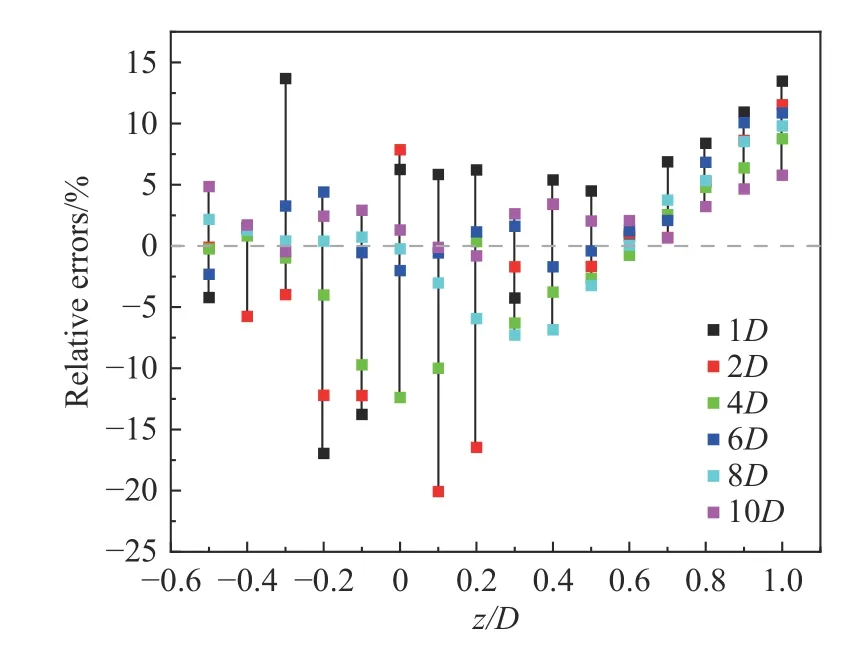
图12 垂直剖面的相对误差分析Fig.12 Relative errors analysis of vertical profiles

4 结论

本文基于双高斯函数，利用流量守恒定理并通过旋转修正推导了一个新的三维尾流模型，该尾流模型考虑了风切变的影响，并且能够描述整个尾流区域的三维变化特征。同时，使用两台陆基激光雷达测量了风场的自由流信息以及尾流信息，利用实测的风场数据在水平剖面以及垂直剖面分别对三维尾流模型进行了对比验证，结论如下：

1）和以往的尾流模型不同，本文提出的尾流模型考虑了整个尾流区域的三维变化特征，假设近尾流分布为双高斯形，远尾流分布为单高斯形，并通过旋转修正的方法考虑了风切变对垂直方向尾流分布的影响。

2）通过激光雷达捕获的实验数据可知：在水平方向，近尾流区尾流分布类似于对称双高斯形，远尾流区类似于对称高斯形；而垂直方向由于风切变的影响呈现出非对称分布，在近尾流区尾流分布类似于非对称双高斯形，在远尾流区类似于非对称高斯形。

3）利用风力机下游6 个位置的实验数据分别对三维尾流模型水平以及垂直方向预测曲线进行了对比验证，结果表明：从整体上看，三维尾流模型能够较好地预测尾流的三维特征，其平均相对误差大部分都在5%以内，但是由于近尾流的湍流变化复杂，对于垂直剖面的近尾流区（x=1D，x=2D）的预测误差稍大，平均相对误差达到了7%。

本文提出的三维尾流模型具有良好的预测精度，且计算成本低，对非均匀风电场布局优化、控制策略等具有潜在的贡献。该研究只针对单风力机的尾流，而对于多风力机的叠加尾流分析则还需要进一步修正尾流模型。