基于区域候选网络的矢量线要素自动化简方法
2024-01-08江宝得许少芬
江宝得,许少芬,巫 勇,王 淼
1. 中国地质大学(武汉)计算机学院,湖北 武汉 430074; 2. 中国地质大学(武汉)国家地理信息系统工程技术研究中心,湖北 武汉 430074
线要素自动化简一直是空间数据多尺度表达、网络传输,以及地图制图综合中的重要研究内容[1-2]。化简的目标是在保持线要素整体结构特征的前提下,尽可能删除线要素上不重要的坐标点,且满足目标比例尺的精度要求[3]。传统的线要素化简方法主要通过人为分析认知规律,总结制图经验,并抽象出计算机能理解的制图约束,然后编译成计算机程序来实现[4]。这类经典的算法有基于顶点与两点连线垂直距离阈值规则的Douglas-Peucker(DP)算法[5]、基于最小可视对象认知规则的Li-Openshaw算法[6]、基于有效面积概念的Visvalingam-Whyatt(VW)算法[7]、基于点到弦的距离与弦长比的垂比弦法[8],以及对线弯曲进行归纳组合的Wang-Muller算法[9]等。然而,这些线化简算法主要基于有限的制图案例抽象出的制图规范来实现[10],算法的化简效果高度依赖算法参数和阈值的确定,容易受到制图人员的经验、主观认知及视觉感受等诸多模糊因素的影响[11],难以满足不同应用场景的自适应化简需求[12-13]。
机器学习方法的出现提供了一种基于数据驱动的制图综合范式[14],通过学习某一制图综合环境下隐藏在制图员已有的化简案例中的特征指标间的模糊关系,得到适用于同样环境下的与制图员思维相近的综合决策模型[15-16],从而推动了自动制图综合的智能化发展[17]。目前已有不少学者提出了基于机器学习线化简方法,如利用K-means进行非监督学习,实现对不同形态特征线要素的识别与化简[18];利用支持向量机对化简单元进行二分类取舍进行线化简[19];融合利用图形、图像特征的集成学习进行智能线化简[12]。然而,这些基于机器学习的方法难以学习隐含在化简案例中深层次的综合知识,智能化程度仍有待提高[1]。
深度学习是一种向更深层次发展的机器学习方法,其中卷积神经网络具有强大的特征提取能力,能够从已有图形案例中自动学习相关知识。目前在地图综合领域,一些基于深度学习的方法被用于建筑物及聚落群[20-22]的化简研究。在线要素化简方面,文献[1]将U-Net[23]应用于山区道路的化简综合,但化简结果并不理想,且停留在栅格阶段;文献[24]使用Pix2Pix[25]来学习线要素的化简案例,自动生成化简结果,但该化简结果依然是栅格,需要在栅格转矢量后采用DP算法[5]进一步进行矢量化简;文献[2]提出一种编码解码网络,通过多层隐藏层实现对输入节点逐层省略,从而达到线化简目的,但是该方法因受结构本身的限制只能有固定长度的输入和输出,在不同化简场景中有可能需要改变神经元数量并重新训练模型来满足化简需求,且化简结果无法保持原有矢量坐标点的位置信息。
综上所述,传统的线化简方法和基于机器学习的线化简方法在智能化程度方面仍有待改进,而现有基于深度学习的线要素化简方法难以直接得到矢量化简结果。因此,本文提出一种基于区域候选网络的矢量线要素自动化简方法,通过改进区域候选框的生成方式,设计一种能够融合利用线要素矢量坐标点信息和栅格卷积特征的弯曲提取模型,并通过已有线化简案例进行训练学习,实现线要素矢量到矢量的自动化简。
1 研究方法
为了实现矢量线要素的自动化简,本文借鉴深度学习的目标检测算法思想,提出一种基于候选区域网络,可端到端训练的矢量线要素化简模型。其思想是以线要素上的弯曲单元作为化简单元[26],将线要素的化简过程视为识别线要素的弯曲单元,删掉非必要弯曲单元的坐标点问题。本文模型主要由3个部分组成(图1):①利用深度卷积网络MobileNetsv2[27]提取矢量线要素栅格化后的卷积特征;②使用改进的区域候选网络(region proposal network,RPN)[28]算法,结合矢量线要素的坐标信息,生成可能的线要素弯曲组合候选框;③裁剪出候选框对应的卷积特征图,利用ROI(region of interest)池化层[29]统一特征图的大小,并通过全卷积网络FCNs[30]进行二分类实现线要素弯曲特征的提取,最后通过删除弯曲单元实现线要素化简。本文方法能够实现端到端的训练,且线要素的化简结果直接是矢量格式。下面对模型的各组成部分进行详细介绍。

图1 线化简模型总体架构Fig.1 Overview of the proposed polyline simplification model
1.1 线要素卷积特征提取
为了能够利用卷积神经网络进行线要素弯曲特征提取,需要先将矢量线要素转换为栅格格式,并裁剪成卷积网络所需输入大小。同时,为了能够在识别弯曲特征后,找出弯曲所对应的原始矢量线要素坐标位置,需要在矢量线要素栅格化时记录线要素上每个坐标所对应的栅格单元位置,然后利用MobileNetV2[27]对栅格线要素进行卷积特征提取。MobileNetV2是Google提出的一种轻量级的神经网络,训练参数较少,应用于栅格化后的线要素弯曲特征提取,能够有效的防止模型过拟合,同时提高模型的训练效率。相较于标准的卷积操作,MobileNetV2采用了一种深度可分离卷积,即将标准卷积分为1个1×1的点卷积和一个深度卷积。图2给出了相关网络结构说明,其中图2(a)为标准卷积,卷积大小为Dk×Dk×M,输入数据大小为Dk×M×N;图2(b)为深度卷积,将M个Dk×Dk的卷积运用到M个通道中;图2(c)为N个1×1×M的逐点卷积,用来组合每个通道的输出。深度可分离卷积就是用深度卷积和逐点卷积来代替标准卷积,并在深度卷积和逐点卷积后面各加1层批量归一化层和1层ReLU激活函数层,这种方法能够有效减少计算量,降低模型的大小。图2(d)为MobileNetV2进行特征提取的结构流程,模型的输入为3×1024×1024的栅格线要素图像,输出为1280×32×32的线要素卷积特征。图3展示了使用卷积网络提取到线要素的特征,其中,图3(a)为最后一层网络所输出的大小为32×32特征图的前32个单通道特征图结果,图3(b)中从左至右依次为原图和第5层、第10层、第15层及第17层卷积块输出的所有单通道特征图1∶1融合后的整体特征图。提取到的特征图能够为线要素上的弯曲判别提供依据。

图3 线要素卷积特征提取Fig.3 The convolutional features extracted of polylines
1.2 线要素弯曲候选框生成
线要素的弯曲及弯曲程度是对线要素地理单元特征的抽象表达[26],常用的线要素弯曲特征识别是利用计算几何中的Delaunay三角网实现[26]。受计算机视觉中目标检测思想的启发,本文采用改进的RPN算法(图4)来实现线要素弯曲化简单元的特征检测。RPN是在faster R-CNN[28]算法中被首次提出,它引入了锚点的概念,即位置和大小固定的候选框。由于RPN生成锚点的方式是通过遍历特征图并在每个像素点上生成k个候选框(通常情况下k默认为9,由3种大小和3种长宽比组合而成);然后将每个像素上的k个候选框分别输入到两个并行的卷积分支(如图4中的分类层和位移回归层),得到候选框的分类评分及需调整的回归位移;最后从筛选出的候选框中检测出与特征位置相匹配的目标候选框。然而,如果将RPN候选框的生成方式直接应用到线要素弯曲特征检测中会存在以下问题:①固定大小和长宽比的候选框不足以概括线要素上的弯曲情况;②线要素特征在卷积特征图上的有效信息稀疏,如果在特征图的每个像素上都生成候选框则计算量巨大,计算效率低。因此,本文对原有的候选框生成算法进行改进。考虑到每张特征图像上对应的矢量线要素坐标点数量远少于特征图的像素点个数,本文根据矢量线要素上的坐标点可能构成的弯曲方式生成候选框,如图5所示。首先逐条获取线要素上的所有坐标点,假设为P1,P2,…,P7,依次计算可能构成的弯曲点组合(P1,P2),(P1,P2,P3),…,(P1,P2,…,P7),(P2,P3),(P2,P3,P4),…,(P2,P3,…,P7),…,(P6,P7),以各弯曲点组合的最小外包矩形作为弯曲候选框,对于有n个坐标点的线段(n>1),本文方法生成的候选框数量为(n-1)+(n-2)+…+2+1=n(n-1)/2个。由于CNN网络对输入图像的大小有要求,因此需要采用固定大小的窗口对线要素进行分割。本文试验数据进行分割后得到1905张输入图像,总共包含6 653 298个候选框,平均每张图生成约3500个候选框,小于原始RPN网络中每张图需要生成的9×32×32=9216个候选框,在后续的训练过程中,模型还将采用ROI交并比及最大值抑制等方法来实现正负样本的平衡,从而进一步减少候选框数量。因此,这样生成的候选框具有以下优点:①极大地减少了候选框的数量,且候选框的长宽比可以根据线要素上可能的弯曲形状而定,能够更准确地提取线要素上的弯曲;②基于线要素上的坐标点所生成的候选框来提取线要素弯曲的卷积特征,可以统一矢量线要素的坐标信息与栅格卷积特征的表达,以便在利用卷积网络进行化简时,能够使化简结果与化简样本的坐标点对应,进而保留原始线要素上的矢量坐标点信息。
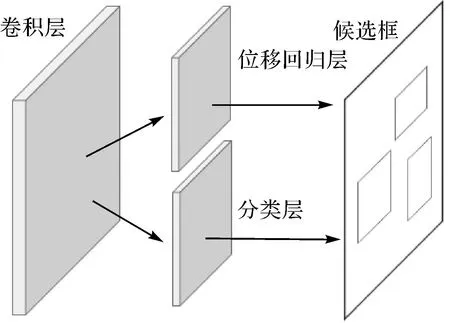
图4 RPN的结构Fig.4 Architecture of the RPN
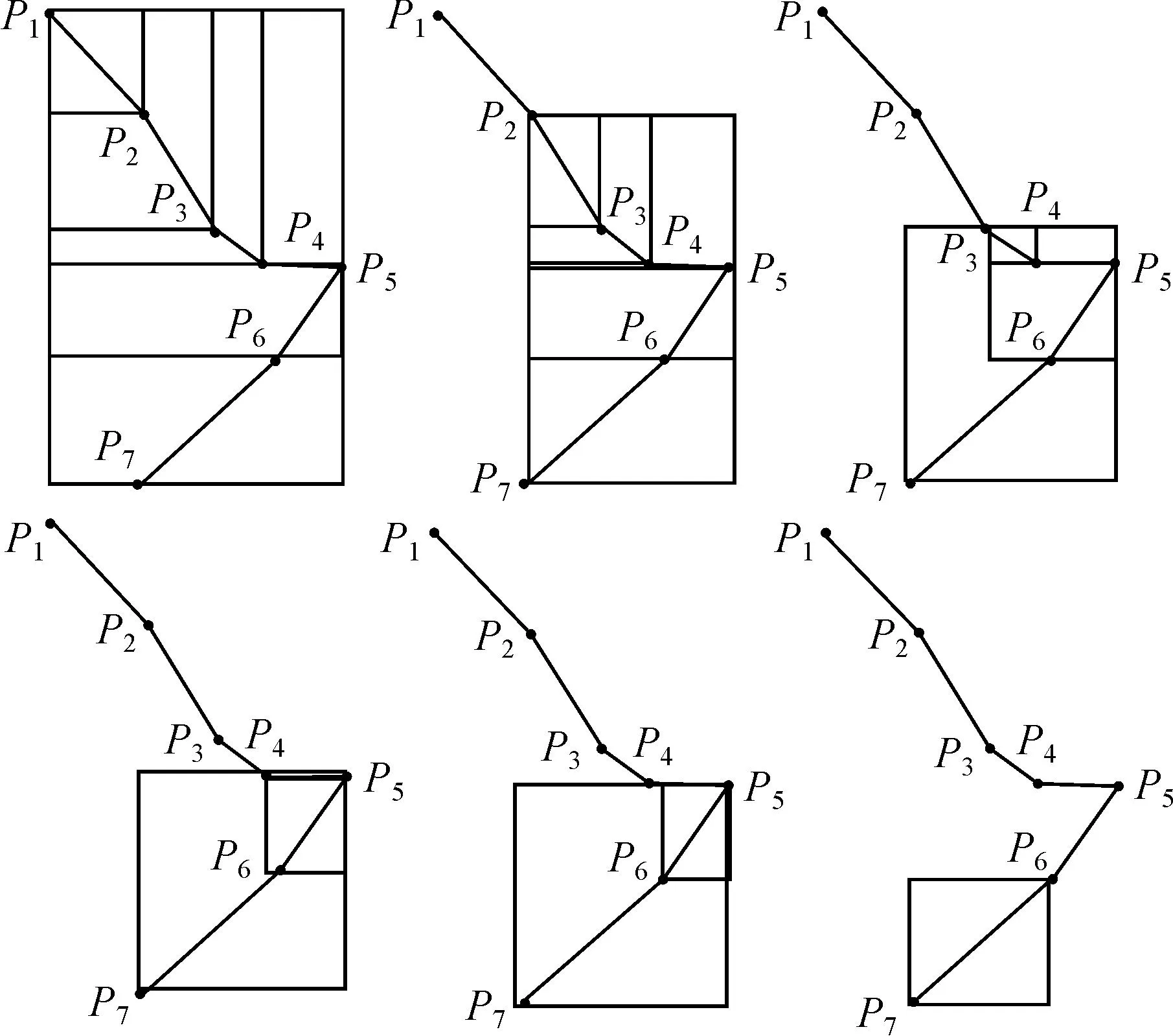
图5 改进后的候选框生成方法Fig.5 Improved generation of region proposal
1.3 线要素弯曲识别与化简
为了实现线要素化简,在改进的RPN生成的各种可能弯曲组合候选框的基础上, 需要进一步根据栅格线要素的卷积特征对候选框进行分类,以获得真实弯曲对应的目标框。其方法是利用生成的候选框从线要素卷积特征中裁剪出候选框相应的特征图,因为候选框代表可能的弯曲组合,所以对裁剪出的特征图进行分类,得到判断为正的目标框即为待化简的弯曲检测框。本文采用FCN[30]网络来实现分类操作,由于FCN要求固定的输入图像大小,而不同候选框对应的卷积特征图的大小各异,如果采用裁剪或缩放等方式来改变目标图像大小势必会改变它的形状特征,因此,本文采用ROI池化[29]来统一特征图尺寸,即将最后一层卷积层输出的特征图以及生成的n个ROI坐标,根据原图与特征图的比例,将ROI映射到特征图对应的位置上(经过前面卷积层的特征提取,图像尺寸已经缩小32倍,因此输入的ROI也要缩小32倍),将映射后的区域划分为相同的块(块的数量由输出的维度大小决定,本文模型块的数量为7×7),然后对每个块做最大池化操作,从而得到相同大小的特征图。对统一大小的卷积特征进行展平,输入到两个全连接层,通过分类卷积层进行二分类判断,保留判断为正的候选框即为识别的线要素弯曲单元的位置,如图6所示。根据1.2节中候选框的生成方式可知,从保留的候选框中可以获取其对应的待化简弯曲单元的坐标点序列,基于弯曲的线化简思想[26],对识别到的弯曲单元坐标点序列进行删除,仅保留弯曲的首尾点作为化简后的线要素顶点,从而实现线要素化简。

图6 弯曲单元检测示意Fig.6 The bending element detected
2 试验与结果分析
2.1 试验数据
本文利用公开的全球海岸线数据集GSHHG[31]进行模型训练和试验验证,该数据集来源于3个公开的数据集WVS、WDBII及AC,并经过了人工加工处理,数据集质量较高。该数据集有5种分辨率,分别为Full、High、Intermediate、Low、Crude;其中Full分辨率数据集对应的比例尺为1∶10万,剩下的每种比例尺依次减少80%的坐标点数量。选用Full和High分辨率数据集分别作为训练样本和标签,对应的起止比例尺分别为1∶10万和1∶25万。本文从中选取新西兰的3个主要岛屿的海岸线作为研究数据,其中南岛和北岛作为训练数据,Stewart岛作为测试数据。训练数据集与测试数据集相关信息见表1。
2.2 试验流程
本文的试验流程分为模型训练与模型测试两个阶段。在模型训练阶段(图7),首先基于化简前矢量线数据生成栅格数据及候选框数据,并基于化简后矢量线数据构建标签数据,使用固定大小的滑动窗口对栅格数据进行切割;将切割后的栅格数据和候选框数据输入网络,训练网络预测目标框,计算得到的目标框与切割后的标签数据之间的损失值;使用Adam优化器对模型的参数进行优化,并迭代训练模型直到损失函数收敛或达到最大迭代次数,训练完成后保存训练好的模型。在测试阶段,使用训练好的模型对测试数据集中生成的栅格线要素图像和候选框数据进行目标框预测,即可完成测试数据的弯曲检测与线化简。

图7 模型训练流程Fig.7 Model training flowchart
2.3 试验设置
本文方法所需的输入训练数据包括分割得到的固定大小的栅格线要素图像,以及分别根据化简前后的线要素坐标点生成的候选框数据和标签数据。由于模型的训练及测试需要先将矢量线要素转换为栅格数据,因此需要确定转换后栅格数据的分辨率。根据文献[6],矢量线要素转栅格操作中转换后的栅格图像分辨率计算公式为
Fc=D/S
(1)
式中,Fc为栅格像元分辨率;S为线要素比例尺;D为最小可分辨对象(SVO),根据文献[3]SVO为0.2 mm。为了确保栅格化后的线要素细节清晰可见,令Fc=D/2S,所以比例尺为1∶10万的矢量线要素栅格化后的图像分辨率大小为:Fc=0.5×(0.2 mm×100 000)=10 m。
另外,为了避免栅格线要素的信息过于稀疏,影响模型的精度,在线要素栅格化时,将画笔宽度设置为5个像素。本文的试验平台基于PyTorch框架构建、训练和测试,模型采用的骨干网络为MobileNetsV2,试验环境所采用的操作系统为Ubuntu 18.04.5 LTS,GPU硬件配置为两块10GB显存的Nvidia GeForce RTX3080,同时使用CUDA11.1进行计算加速。训练时采用预热学习策略,首先采用5个epoch进行预热训练,将模型的初始学习逐步上升到0.001,然后采用按需调整学习率策略,当连续2个epoch的损失函数不下降时,学习率变为原来的1/3,直至损失收敛。模型的输入图像大小为1024×1024,窗口重叠率为50%,栅格分辨率为10 m。试验时在模型中添加了批量归一化层来减少模型的损失,以加速模型收敛,并使用Adam优化器[32]对模型损失进行优化。通过使用标签进行监督训练,最终得到模型的像素平均精度为87.17%。
2.4 评价指标
本文基于每个像素的平均精度(mAP)指标来定量评价所提出的线化简模型精度。mAP值可通过积分计算弯曲提取结果的精确率-召回率(precision-recall,P-R)曲线与坐标轴所围成的下方面积得到。精确率(precision)和召回率(recall)的计算公式为
(2)
式中,TP指真正例(对弯曲单元的真实预测);FP指假正例(将非弯曲单元预测为弯曲单元);TN为假负例(将弯曲单元预测为非弯曲单元);FN为正负例(对非弯曲单元的真实预测)。这些指标可通过计算预测得到的弯曲定位目标框与真实标签之间的交并比(intersection over union,IoU)获得,只有IoU大于某一阈值时,弯曲特征才被标记为正样例。
模型训练的损失函数能够判断模型的训练效果及其是否收敛,但是仅仅采用模型自身的评估函数无法准确地说明线要素化简的效果,好的线化简结果不仅需要整体上损失较少,也需要在细节上保留线要素的形状特征,例如,删除线要素上几个关键的坐标点,对损失函数的影响可能微乎其微,但是对线化简的结构影响很明显[1],因此还需要对化简后的线进行图形特征指标方面的评价。根据文献[33],采用以下6种指标对模型的化简效果进行评价:①坐标点压缩比,通过比较模型化简结果与标签数据坐标点的压缩比可以说明模型的化简效果,压缩比越大,保留的坐标点越少,化简效果越好;②坐标标准偏差,通过计算化简前后线要素上坐标点偏移距离的标准差,能够体现化简后的线要素与化简前线要素走向的一致性,标准差越小,化简前后线要素的走向越一致,化简效果越好;③角度变化百分比,是指线化简后微摆动的减少,保留越多较大角度变化的化简效果越好;④总长度差;⑤总面积差;(④、⑤两种测度综合表明了线要素总的几何位移,产生的位移越少,化简效果越好)⑥曲线段数的百分比变化,制图人员在综合制图的时候会将线要素平滑化,但是角度减少不一定意味着曲线段数减少,因此使用曲线段数的指标能很好地体现制图过程中图形几何变化的特点,曲线段数减少越小,化简效果越好。
2.5 试验结果与分析
试验化简结果如图8所示,由图8可以看出,模型的化简结果与原有线要素的几何形态高度相似,较好地保持了原有线要素的几何结构特征。
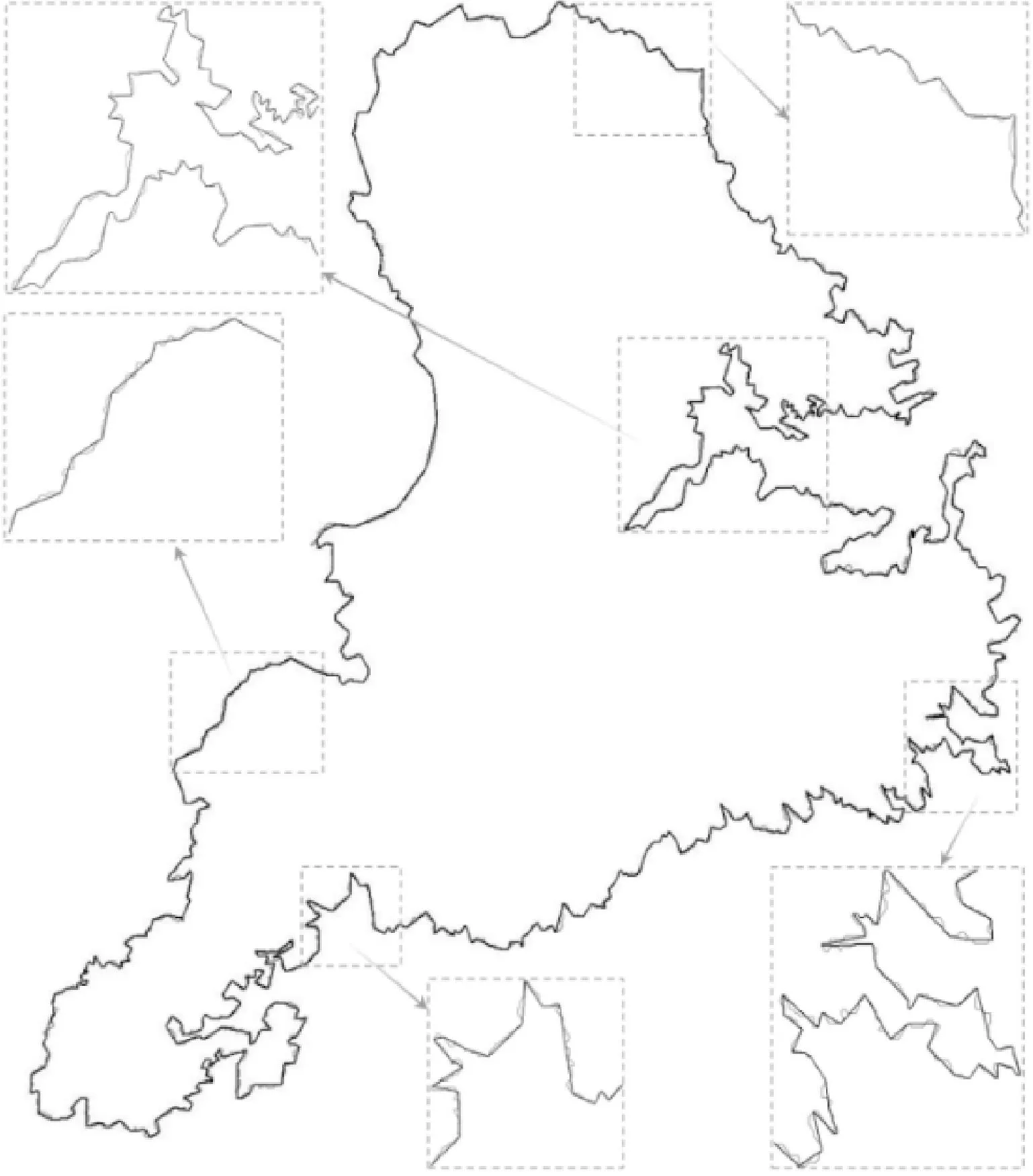
图8 Stewart岛海岸线化简前后对比Fig.8 Results before and after simplification of the coastline of Stewart Island
将本文的化简结果与标签数据及VW算法化简结果进行量化图形特征指标对比分析(表2)。其中,标签数据是基于DP化简算法并结合人工拓扑纠正所得[31]。VW是一种广泛使用地图线要素化简算法,常用于海岸线等自然要素的化简,能较好地保持自然线要素的几何特征[7],与其对比具有一定的代表性。VW算法的参数为节点的有效面积,本文使用点的数量作为广义尺度的度量,参照标签数据的坐标点压缩率调整VW算法的参数,使化简后的线要素坐标点数与标签数据接近。由表2可以看出,本文方法的线化简结果各项指标整体上与标签数据接近,其中,坐标点压缩比比标签数据低4.80%,总长度差比标签低0.03%,坐标标准偏差比标签低3.03 m,角度变化比标签低3.22%,曲线段数变化比标签低4.65%。即除了坐标点压缩比,其他指标都略优于标签数据,说明本文提出的基于深度学习的自动线化简方法能够学习到标签数据的化简知识,较好地保持了线要素的整体结构特征。VW算法在坐标点压缩比指标上与标签接近,略优于本文方法,但在其余几项定量评价指标方面都不及标签数据及本文提出的方法,这一点从图9中3种方法的化简结果细节对比也可以看出,其中,VW算法在部分细节发生形变,而本文的化简结果基本上与标签数据接近,在局部化简细节方面比VW要好,这主要是因为标签的化简结果是在DP算法化简基础上经过了人为调整,以消除部分拓扑错误和化简不合理的之处,而本文方法又能很好地学习到标签的化简效果。进一步,对化简结果进行视觉缓冲区限差[13]分析,理论上, 化简后的线要素与原始线要素的视觉缓冲区Sab的重叠率越高,说明与原始线要素的相似程度越高,形态保持越好,由图10可以看出,3种方法化简结果的缓冲区限差值都在80%左右,比较接近,说明3种方法化简结果都能较好地保持原始线要素形态特征,而本文方法的视觉缓冲区限差值与标签数据更接近,说明本文的方法能够较好地学习标签的化简知识,化简结果符合形态特征保持要求。

表2 线化简效果定量评价

图9 化简细节Fig.9 Simplification details
2.6 扩展试验
2.6.1 栅格化参数对比分析
线要素栅格化时的分辨率关乎栅格线要素的信息稀疏问题,过小的分辨率会导致栅格化后的线要素在栅格图像上所占的信息量少,使得在卷积特征提取过程中,因频繁的下采样操作而导致特征丢失,降低模型的精确率。影响栅格线要素在栅格图像上所占信息比的参数主要有两个:栅格图像的像元分辨率和栅格化线要素时设置的画笔宽度(笔宽)。当像元分辨率一定的情况下,画笔越宽,同一条线要素在栅格化后所占的图像信息比越高。而根据上文可知,本文方法像元分辨率Fc设置为10 m。因此,要提高栅格化后所占的图像信息比,就需要增大栅格化时的笔宽。但过大的笔宽又可能导致线要素边缘特征模糊,如图11所给出的像元分辨率为10 m时不同笔宽生成的栅格线结果,可以看出当笔宽W=5像素时,线要素的坐标点、弯曲特征等较为清晰,而当笔宽W=50像素时,线要素上出现了大量的边缘重叠,导致要素坐标点及弯曲特征被覆盖。
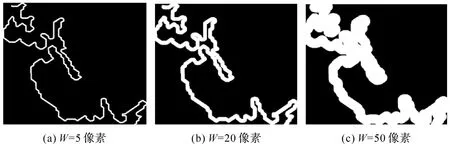
图11 同一线要素不同画笔宽度的栅格图像Fig.11 Raster picture of the same polyline with different pen width
为了探明不同的笔宽对化简结果的影响,本文在保持像元分辨率及其他变量不变的情况下,将画笔宽度W分别设置为2、5、20及50像素进行对比分析,以找出合适的栅格化笔宽。图12给出了像元分辨率为10 m时不同笔宽的测试集化简结果,表3为其对应定量评价指标值。由图12中化简结果对比分析可知,笔宽为5像素的线要素化简结果(b)前后相似度最高,形状特征保持最好;同样,由表3相应评价指标也可以看出,此时模型的准确率mAP值最高,达到87.17%,几何评价指标中有3个指标表现都优于其他对比结果,分别是总长度变化13.56%、总面积差0.05%、坐标标准偏差76.68 m,而其余3个几何评价指标值,如坐标点压缩比80.01%、角度变化73.29%和曲线段数变化77.06%与对比试验中最佳的指标值都接近,说明当前笔宽下线要素化简效果比其他对比结果都要好。另外,对表3中结果集(a)—(d)的模型精度变化情况分析可知,当笔宽逐渐增大时,模型的精度mAP值先升后降,当笔宽为5像素时,模型的精度最高,这说明栅格化时,笔宽并非越大越好,图12也证明了这一点。因此,由以上4种笔宽的对比试验的定量分析可知,当初始比例尺为1∶10万时,矢量线要素在栅格化时图像分辨率大小为10 m,画笔宽度为5个像素时的化简效果最佳。

表3 不同像元分辨率化简结果的定量评价

图12 像元分辨率Fc=10 m时不同画笔宽度的化简结果Fig.12 Simplification results with pixel sizes Fc=10 m and different pen widths
2.6.2 不同骨干网络对比分析
栅格图像的卷积特征提取对线要素的弯曲准确识别至关重要。在目标检测中,常用的特征提取骨干网络有VGG16[34]、MobilenetV2及FPN[35-36]等,考虑到线要素的特征稀疏,而FPN模型的参数量较大,因此,本文选择模型较轻量的VGG16和MobileNetV2作为特征提取骨干网络进行效果对比分析。在这两种模型的训练及测试过程中,除了骨干网络之外,其他试验环境与参数设置均相同。图13分别给出了二者准确率、图像测试耗时、损失(loss)及学习率(learning rate)的变化对比。由图13(a)可以看出,VGG16与MobileNetV2分别作为骨干网络模型的准确率十分接近,均在87%左右,但因为VGG16的参数量大于MobileNetV2,所以在使用训练好的模型对测试数据进行预测时,MobileNetV2预测每张图像用时仅需0.01 s,明显快于VGG16的0.045 s(图13(b)),在本文的测试数据集上,MobileNetV2测试完71张图像用时0.823 s,而VGG16总共用时3.263 s。另外,从训练过程中模型的损失和学习率变化可知,MobileNetV2(图13(c))比VGG16(图13(d))更快达到损失收敛,且损失收敛到更低值0.038 5,VGG16则收敛到0.177 4。因此综合考虑模型的精度和效率,MobileNetV2更适用于作为本文模型的卷积特征提取的骨干网络。

图13 不同骨干网络模型的验证评价Fig.13 Model validation evaluation under different backbone
2.6.3 跨尺度化简分析
本文方法的测试验证是基于公开的GSHHG海岸线数据集,该数据集包含多种分辨率数据,分别对应多个化简尺度,其中Full分辨率为1∶10万,High分辨率为1∶25万,Intermediate分辨率为1∶50万。为了验证本文方法进行跨尺度的化简效果,下面以1∶10万作为起始比例尺,分别对海岸线数据开展从1∶10万到1∶25万再从1∶25万到1∶50万的递进式跨尺度化简,和直接从1∶10万到1∶50万的跨越式尺度化简试验。两种化简模式化简后得到的1∶50万的比例尺数据分别包含114个和126个坐标点,相应坐标压缩率分别为97.2%及96.8%,化简结果如图14所示。由图14可以看出,基于本文方法能够实现跨尺度化简,且两种跨尺度化简方式坐标压缩率较接近。但对比标签化简结果(图14(a))可知,在几何形态保持方面,从1∶10万跨尺度化简到1∶50万的化简结果(图14(c)),不如先从1∶10万化简到1∶25万再从1∶25万化简到1∶50万(图14(b))的化简效果。其原因与化简过程中正样本与负样本的比例有关,跨越的尺度越大,正样本的数量越少而负样本的数量越多,从而影响模型的训练准确率。
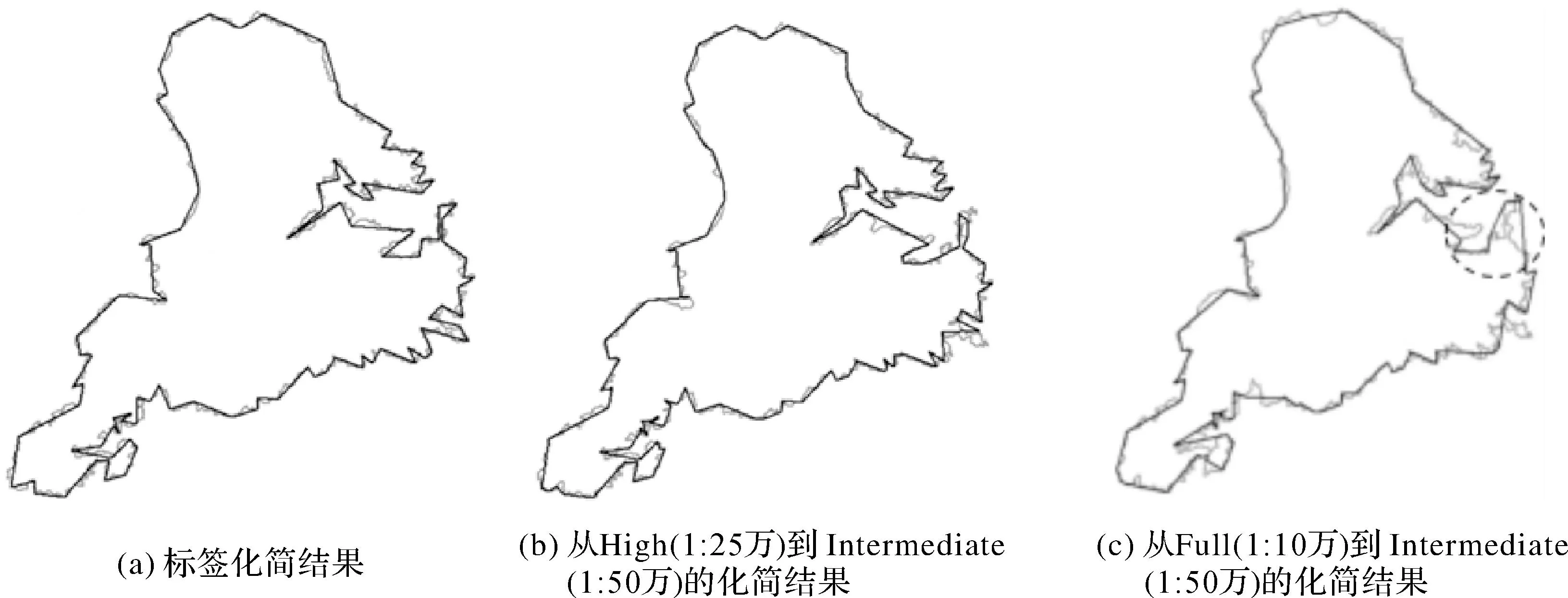
图14 跨尺度化简结果Fig.14 Cross-scale simplification result
2.6.4 不同类型线要素化简
不同类型线要素的化简规则存在着较大差异,为了验证本文方法在其他类型线要素上化简的泛化效果,从OpenStreetMap中获取新西兰某地区的河流水系数据,并采用DP算法生成合适的标签数据进行试验。数据集化简前后的比例尺分别为1∶10万和1∶25万,使用本文的模型化简后得到的试验结果坐标点压缩率为80%,化简细节如图15所示。可以看出本文提出的化简方法保留了良好的形状特征。需要注意的是,水系及路网等类型的线要素具有明显的分支特点,需要在交点处对线要素进行打断处理,从而生成可被化简的训练数据。此外,本文方法仅能实现化简效果,而不能实现选取,在水网及路网等类型的数据中,要素的选取是制图综合中的重要步骤。

图15 水系化简结果Fig.15 Water system simplification results
3 结 论
矢量线要素的自动化简是制图综合中的重要问题,本文针对现有基于深度学习的线化简方法无法实现矢量到矢量的化简问题,提出了一种基于区域候选网络、可端到端训练的矢量线要素自动化简模型。其思想是以线要素上的弯曲单元作为化简单元,将线要素的化简过程视为识别线要素的弯曲单元,并删掉非必要弯曲单元的问题。本文方法主要由线要素卷积特征提取、弯曲候选框生成及弯曲单元化简3个部分组成。卷积特征提取部分以MobileNetsV2作为骨干网络,实现了线要素栅格化后的卷积特征提取。在弯曲候选框生成过程中,提出了一种利用矢量线要素坐标点高效生成区域候选框的方法,建立了线要素栅格卷积特征与矢量坐标点的对应关系,实现了卷积特征与坐标信息的统一表征,高效生成了线要素上可能构成弯曲单元的候选框组合方式,提高了模型训练效率。最后在统一线要素弯曲特征图大小的基础上,利用二分类实现对线要素化简弯曲单元的自动识别,并通过删除弯曲单元实现线化简。通过在GSHHG数据集上进行线化简综合试验,结果表明,本文方法能够从已有线化简案例中学习相关化简知识,相较于其他采用深度学习的线化简方法,本文方法能充分利用线要素的矢量特征及栅格特征,自动完成线要素弯曲特征的准确定位,最终实现可端到端训练的矢量到矢量线要素自动化简,智能化程度高,且化简结果具有较高的坐标点压缩比,能够较好地保持线要素的形状结构特征。另外,本文的线化简模型轻量,训练简单,可望将其作为单独的模块整合到基于深度学习的遥感图像分割网络中实现二值目标矢量化后的化简,以实现矢量线要素地图的自动提取,也可以被复用到泛在网络环境下多种尺度、多种类型及多种场景的线要素化简的具体任务之中。不过,本文方法亦有不足之处,首先,由于本文的线化简模型是基于弯曲删除的化简思想,无法实现弯曲的夸大、移位,以及线要素选取等综合操作;其次,本文方法在跨尺度的化简细节保持上还可继续优化,着重考虑化简单元正负样本不均衡的问题。后续将结合生成对抗神经网络对线要素化简算法进行改进,使其能更广泛适用于各种地理线要素的自动综合应用需求。
