顾及面积差的层内等效二段线替代法优化声速剖面

肖元弼,彭认灿,董 箭,马政伟,刘 聚1,

1. 海军大连舰艇学院作战软件与仿真研究所, 辽宁 大连 116018; 2. 海军大连舰艇学院战术学博士后科研流动站, 辽宁 大连 116018; 3. 海军大连舰艇学院军事海洋与测绘系, 辽宁 大连 116018; 4. 91388部队, 广东 湛江 524000

对于多波束勘测这种靠声波在水中传播进行测距的测深系统,声速作为最重要的计算参数,其精度的高低将直接影响测深结果。声线跟踪法在追踪波束脚印时需要用到声速剖面(sound velocity profile,SVP),而高采样密度的声速剖面数据会导致声线跟踪法在分层计算和逐层累加过程中耗时较长,降低计算效率。通过简化声速剖面来减少计算层数是提高声线跟踪计算效率的一种最直接方法,但盲目的简化会忽略声速剖面一些特征信息,从而降低测深精度。再加之,多波束测深系统测深覆盖面广、数据量大的特点,因此,需要探究一种在声速剖面简化过程中能兼顾数据精度的方法[1-16]。

道格拉斯-普克法(Douglas-Peucker,D-P)是一种在制图系统中常用的地形特征线简化算法,主要通过观测点到曲线首尾连线的垂直距离作为阈值参考指标,利用几何相似性来简化复杂曲线。若应用于声速剖面简化,其存在的问题是声速剖面横纵坐标分别是速度与深度,其单位不统一将导致几何垂直距离及阈值没有实际物理意义。为解决声速剖面简化问题,国内外学者进行了大量研究。文献[17]提出了一种基于声速最大偏移量(maximum offset of sound velocity,MOV)的D-P改进算法。将声速维度上最大距离作为阈值的参考指标,对采样点进行取舍,相比较D-P算法,MOV算法在声速剖面应用下更为合理,并且能够保留D-P算法对于曲线几何特征保留性强的优势。但该算法以整体水深误差1%作为极限指标,来寻找最优阈值,存在分层内声速剖面等效性不完全合理的情况,尤其在特殊的声速剖面情况下阈值收敛性较差。文献[18]提出了一种基于面积差约束的声速剖面自适应简化方法,通过对所有采样点进行逐点取舍判断,在确保声速剖面精度和基本空间变化结构情况下,简化率和跟踪精度较高,在声速剖面起伏波动频率较高的区域尤为明显。但整体声速剖面运用面积差约束寻找等效替代,会导致层内声速剖面几何特征保持性较差,并且整体计算过程较为复杂。

本文针对声速剖面简化后层间精度不高的情况,提出一种声速剖面自适应分层优化方法——层内等效二段线替代法(in-layer equivalent two-segment line substitution method,IETL)。该方法在实测SVP数据的基础上,对MOV算法进行改良,利用等效面积差作为约束条件,通过构建层内等效二段线,来对层间声速剖面进行优化,以便提高层间声速剖面精度。试验表明,经过本文方法优化后的声速剖面,在保证整体数据精度的基础上,能够进一步提高层间数据精度,尤其在地形波动较大的地区,其潜在的工程应用优势尤为明显。

1 方法与简化模块

1.1 顾及面积差的IETL法

1.1.1 声速剖面简化原则调整

声速剖面简化的主要目的是通过减少声速剖面上的声速点个数来减少声速的分层数,从而提高测深点位置计算效率。但不同于简单的几何优化,声速剖面简化原则最重要的是要保证测深点位置精度,并在此基础上提高声线跟踪效率。因此,传统声速剖面简化原则可归纳为:①保证波束在海底总体测深数据精度;②声速变化相对稳定的区域可合并为一个水层;③不破坏声速剖面结构特征信息,保留特征性较强的采样点。

但传统简化原则存在几个问题,首先原则①由于只考虑整体声速替代剖面简化,而忽略了层间声速剖面等效情况,对于海底地形变化幅度较大的区域(如断崖等),势必会影响测深精度;原则③对于声速剖面变化复杂的水层,是否可以在保证测深精度的情况下,对特征采样点进行改变,以达到简化目的。本文针对问题情况,将简化原则调整为:①保证波束在海底总体及每个水层的测深数据精度;②声速变化相对稳定的区域可合并为一个水层;③不破坏声速剖面结构特征信息,保留或适当改变特征性较强的采样点。

1.1.2 MOV算法

D-P算法是一种简化多段线的常用方法[19],如图1(a)所示。其基本思想是先确定阈值Q,对复杂线段的首尾端点进行连线,再依次计算出原始折线段间其余各点P到该线段的距离Hi,找到其中最大的垂直距离Himax与阈值Q进行比较,计算公式为[19]

(1)

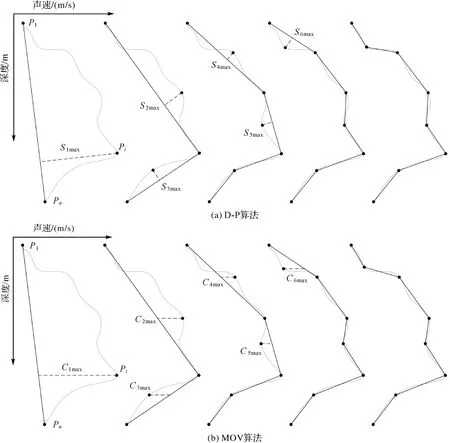
图1 D-P算法与MOV算法Fig.1 D-P algorithm and MOV algorithm

式中,x表示声速;y表示深度;P1表示原始声速剖面第一个点;Pn表示原始声速剖面最后一个点;Pi表示替代声速剖面点。

若Himax≤Q,则除首尾两点,其余各点都删除,算法结束;若Himax>Q,则保留该点Pi,并从该点处分别向首尾两端P1、Pn进行连线,形成两条新的线段P1Pi、PiPn。重复迭代上述步骤,找到各自线段的所有点到新形成线段的最大垂直距离,继续与阈值进行比较,直到所有点到各自线段垂直距离都小于阈值,即完成简化操作。但由于声速剖面纵坐标为深度(单位为m),横坐标为声速(单位为m/s),两者单位不统一使得上述方法的几何连线垂直距离无实际物理意义,导致D-P算法无法应用于SVP简化。

针对D-P算法在SVP方面的应用问题,文献[17]在D-P算法基础上,提出了改进的MOV算法,由点到线段的垂直距离改为声速的最大偏移量,同阈值进行比较。如图1(b)所示,对首尾端点进行连线,依次计算出原始折线段间其余各点到该线段的横坐标偏移量,即声速偏移量Ci,找到最大距离与阈值进行比较,计算公式为[20]

(2)

而对于点的判断保留步骤与D-P算法相同。因此,MOV算法能够很好地解决D-P算法在简化复杂声速剖面时,阈值与垂直距离没有实际物理意义的问题,使得此简化模型能够应用于声速剖面。

等效声速剖面表示若采用某一曲线作为简化声速剖面进行计算得到的测深点位与原始声速剖面得到的测深点位一致,即认为该曲线为等效声速剖面[20]。虽然MOV算法作为D-P模型的改进算法能够对曲线进行最优简化,在设定合适的阈值后,能够将整体测深数据误差控制在1%以内,满足国际海道测量组织(International Hydrographic Organization,IHO)对水深测量的标准,但不同于误差传递,声线跟踪法计算深度是一个累加的过程,可能会存在某一层声速整体偏低,另外一层又整体偏高,与替代声速剖面间偏移量抵消导致测深结果影响不大的情况。因此,整体测深数据误差低并不能说明声速剖面每一层测深误差同样低。对声速剖面而言,每一层的简化曲线并不一定等效于原始声速剖面,在地形变化较大的区域,尤其是声速变化较大的浅水区,简化曲线会对测深数据产生较大的影响。如图1(b)所示,明显其中第三层替代声速剖面与原始声速剖面存在面积差,导致该层部分的声速剖面等效性较差。可见,虽然整体测深数据满足精度要求,但每一层的替代声速剖面并不一定是等效的声速剖面,因此需要对该层进行等效替代。

1.1.3 最大等效面积差提取方法

图2为某一水层声速剖面与等效声速剖面面积差的仿真关系,图中红虚线为简化声速剖面,实线表示原始声速剖面及等效声速剖面面积差的曲线。由图2可以看出,除了水层的两端点外,极值也产生在a、b、c3点,这3点都对应的是替代声速剖面与原始声速剖面的交点处,因此寻找替代声速剖面与原始声速剖面面积差的最值,只需在端点及两条线交点处比对即可。记录下水层中声速剖面面积差的最大值,若最大值符合精度要求,即整个水层的替代声速剖面都符合精度要求,如图2中c点为该水层等效声速剖面面积差的最大值。

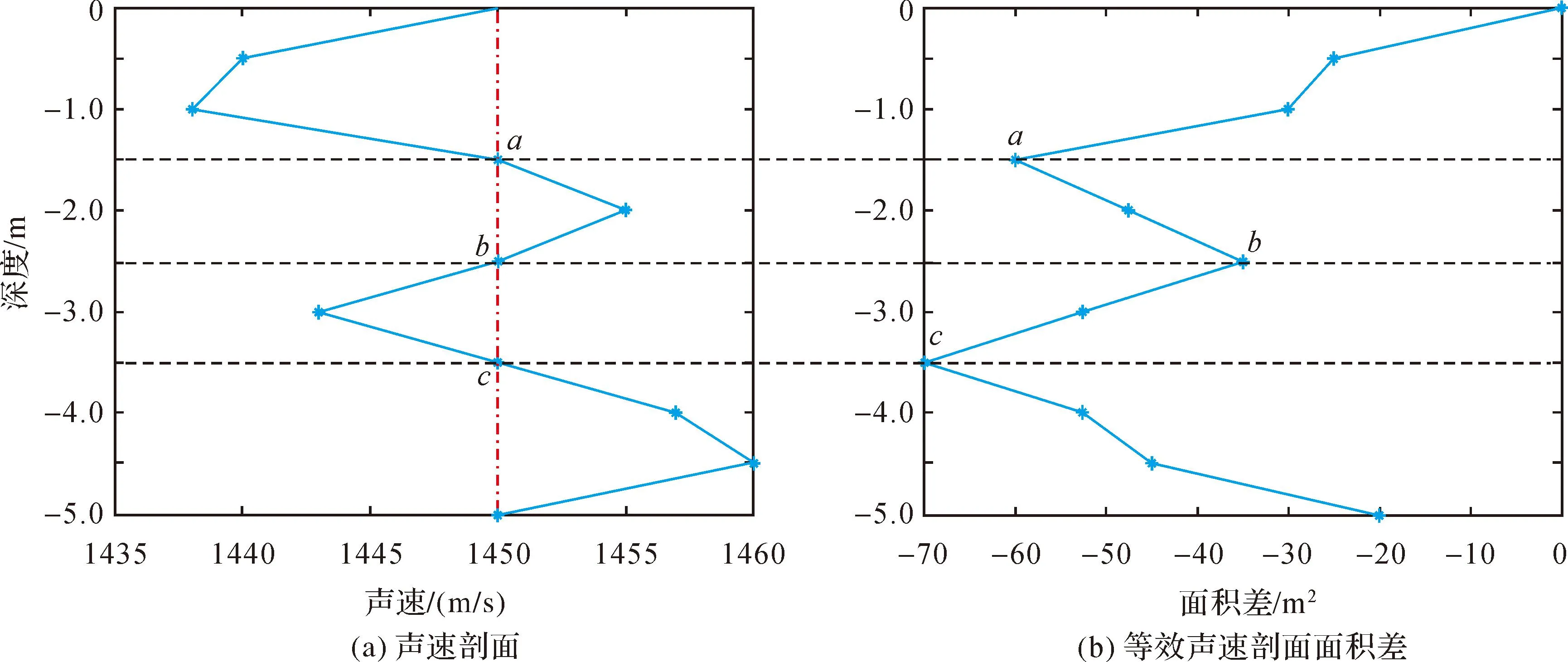
图2 声速剖面与等效声速剖面面积差关系Fig.2 Area difference between SVP and equivalent SVP

面积差与声线跟踪精度的关系模型如下

(3)

式中,εx、εy分别表示水平位移和深度的相对误差,由原始声速剖面声线跟踪得到的测深点坐标(x,y)及替代声速剖面得到的坐标(xt,yt)作参考得到;gi、gt分别表示原始声速剖面的梯度和等效声速剖面的梯度;ΔS为面积差;c0为初始声速;θ0为入射角。式(3)表明在入射角θ0与初始声速c0已知的情况下,相对误差εx、εy只与面积差ΔS有关。可通过比较水层内最大面积差ΔSmax得到相对误差εmax与限差ε0的关系来判断替代声速剖面水层是否需要进行进一步优化。若εmax≤ε0,说明层内替代声速剖面优化程度满足精度指标,保留层内替代声速剖面点不做处理;若εmax>ε0,则说明层内替代声速剖面优化精度不够,需要进一步优化。

1.1.4 层内声速剖面等效替代二段线模型建立

已知,i层间原始声速剖面与y轴(深度轴)围成的面积是固定的Vi,因此其层内声速积分也是一个定值

0.5(y-ya)(x+xa)+0.5(ya+Δy-y)·

(x+xa+Δx)=Vi

(4)

由式(4)可知,深度y相同的情况下存在唯一一点(x,y)分别与i层内两端点(xa,ya)、(xa+Δx,ya+Δy)进行连线得到两条线段(又称二段折线段),并与y轴(深度轴)围成的面积为Vi,即与原始声速剖面所得的面积差值为0,认为该二段折线段为该层等效声速剖面。

如图3(a)所示,对于某一水层,根据MOV算法原始声速剖面的声速偏移量都没有达到阈值k的界限,因此不需要进一步分层,但由图3中可明显看出原始声速剖面与替代声速剖面EG不等效。而对于声速最大偏移量F处所在的深度m线上,存在一点F2分别到E点与G点所形成的线段,与y轴围成的面积与该层原始声速剖面围成的面积等效(图3(b))。

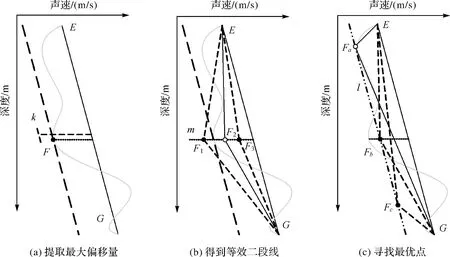
图3 顾及面积差的等效二段线替代法Fig.3 In-layer equivalent two-segment line substitution method considering area difference

式(4)转化为式(5)

(5)

由式(5)可得存在一条直线,该直线上任意一点到两端点(xa,ya)、(xa+Δx,ya+Δy)的连线所形成二段折线段为等效声速剖面,并且该直线的斜率与两端连线的直线斜率相同,如图3(c)中l线所示。

在等效声速剖面点集合所形成的直线l上,存在一点(xt,yt)使得等效声速剖面与原始声速剖面间偏移量差的平方和为最小值(也可理解为净偏移量最小值,为了方便计算采用忽略正负号影响,这里采用平方和),即该点为最优解,是所有替代的等效声速剖面中最接近原始声速剖面的,如图3(c)中Fa所示。为方便寻找最优解,式(6)构造拉格朗日函数求条件极值

F(xt,yt)=f(xt,yt)+λφ(xt,yt)

(6)

式(7)为约束方程由式(4)转化而来

φ(xt,yt)=0.5(yt-ya)(xt+xa)+0.5(ya+
Δy-yt)(xt+xa+Δx)-Vi

(7)

式(8)—式(9)分别表示以最优解(xt,yt)作为新增点,分别与上下两端点连线所形成的两部分替代声速剖面表达式

(8)

(9)

式中,x=g(y)表示原始声速剖面,是个已知的定值。

式(10)为偏移量差的平方和

(10)

将式(7)和式(10)代入式(6),分别对xt、yt、λ求偏导(式(11)—式(13))

(11)

(12)

(13)

可得到最优解(xt,yt),即等效面积差为0作约束条件的最优替代声速剖面二段线拐点。分别计算测点与等效二段线做偏移量差的平方和,计算最小值。

1.2 顾及面积差的等效二段线替代法优化流程

1.2.1IETL方法

直接在层内增加等效声速剖面二段折线,虽然会提高层内数据精度,但同时也会增加整个声速剖面的水层数,降低简化率。若在水层数保持不变的情况下,尽可能对已简化的采样点进行优化,即可在保证简化率的情况下提高替代声速剖面。先从等效声速剖面面积差最大的水层进行分析,如图4(a)所示,该图为经过MOV优化的声速剖面,其中i层等效声速剖面面积差最大,在不增加水层的前提下先分析是否能够对i层两端点Di、Di+1进行优化。对点Di进行分析,把Di-1DiDi+1所在的i-1和i层合并为一层,按照1.1.4节算法,得到最优点DDi代替原Di作为新声速剖面简化点,并记录下DDi与Di+1形成的新水层内等效声速面积差(图4(b));同理,对原i层另外一端点Di+1的分析,把DiDi+1Di+2所在的i和i+1层合并为一层,得到最优点DDi+1,记录下DDi+1与Di形成的新水层内等效声速面积差(图4(c))。对比两个等效声速面积差,若最小值满足精度要求,则将该替代点作为新的保留,继续优化。否则说明该层两端点难以进行优化,需增加新的等效声速剖面点。

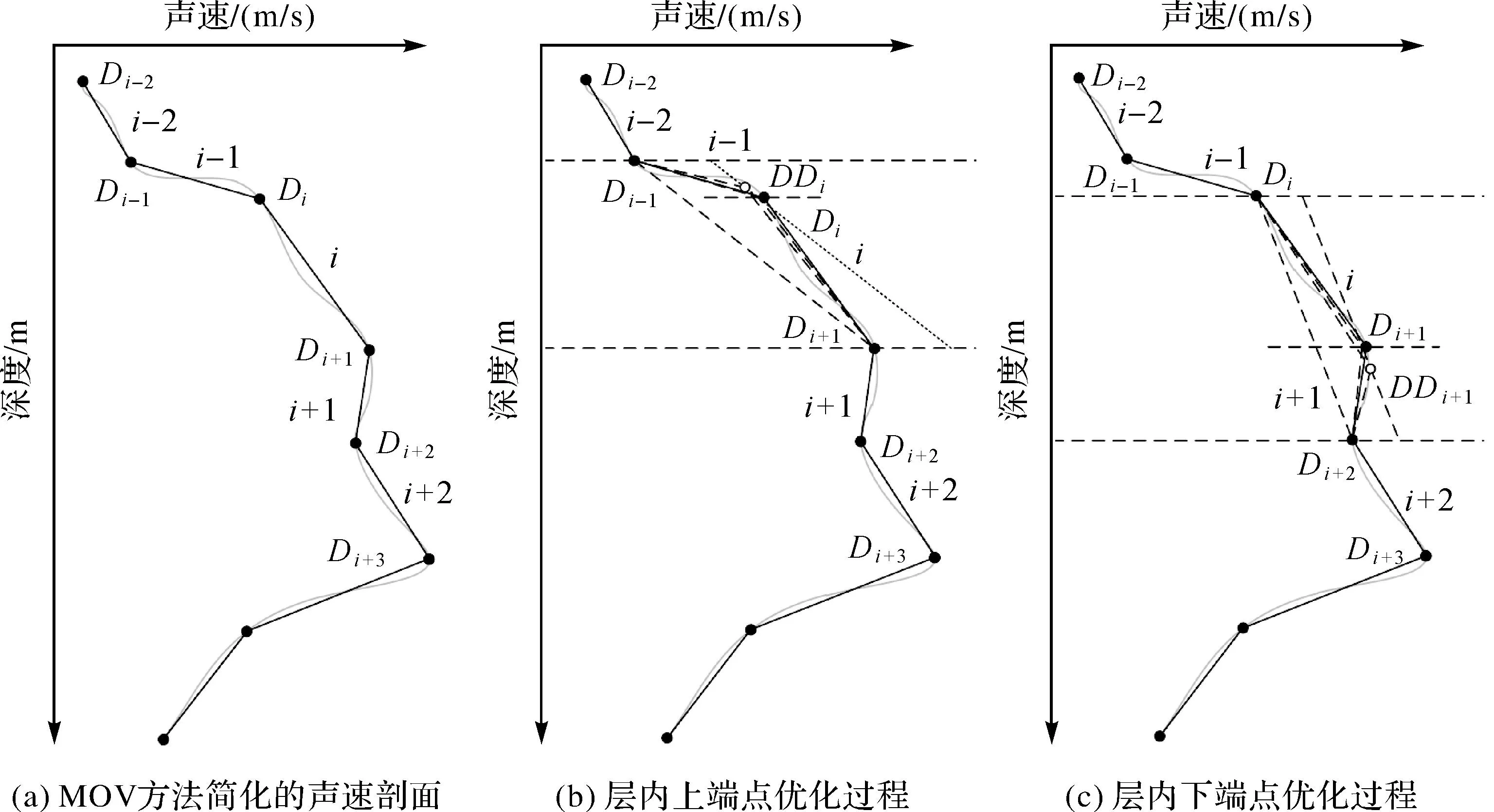
图4 声速剖面层内端点优化替代方法Fig.4 An alternative approach to SVP in-layer endpoint optimization

1.2.2 方法简化模块

根据前文的问题分析,本文方法是顾及面积差的等效二段线声速剖面替代优化法,可归纳为两大模块分别为:MOV算法简化模块和替代优化模块,其中替代优化模块又可分为整体优化模块及层内端点优化模块,如图5所示。

图5 优化模块流程Fig.5 Flowchart of optimization module

MOV算法简化模块用于声速剖面的简化,其核心是1.1.2节所述的MOV算法,主要实现步骤如下。

(1) 数据输入。输入原始声速剖面点集,设定阈值参数T。

(2) 提取声速最大偏移。计算各点的偏移量,并从中提取最大偏移量Cmax。

(3) 剖面线段切割。判断Cmax和T的大小,若Cmax≤T,转至步骤(4);若Cmax>T,保存该点,并将剖面线段在该点处分为两段,并返回步骤(2)。

(4) 数据输出。将原始声速剖面的首尾端点及所有后形成的点记录下,输出为替代声速剖面。

整体优化模块是在MOV算法简化的替代声速剖面基础上,对现有的特征点进行修正或者增加,以便提高声速剖面精度。

(1) 数据输入。输入MOV算法简化模块所得的替代声速剖面点集及原始声速剖面点集。

(2) 提取最大等效面积差的水层。利用1.1.3节方法找到等效面积差最大的所在层,并对该层进行优化分析。

(3) 精度评估A。利用1.1.3节算法,通过最大面积差ΔSmax得到相对误差εmax,若εmax≤ε0,转至步骤(6);若εmax>ε0,则转至步骤(4)。

(4) 对层内端点进行优化。对最大面积差所在的i层端点进行优化,详细情况在层内端点优化模块中说明。

(5) 精度评估B。评估端点进行优化后的i层,利用1.1.3节算法,若εmax≤ε0,则接受新端点替代原简化点,转至步骤(2);若εmax>ε0,则拒绝新端点,并在i层内添加新的等效点,形成新的替代声速剖面,转至步骤(2)。

(6) 输出数据。输出新的声速替代剖面。

层内端点优化模块的步骤如下。

(1) 数据输入。输入最大等效面积差所在i层的替代声速剖面点集和原始声速剖面点集。

(2) 对i层内两端点进行替代分析。分析上端点,将i-1层与i层合并为一层,建立等效面积线;分析下端点,将i层与i+1层合并为一层,建立等效面积线。

(3) 得到最接近原始声速剖面的点。在替代声速点所得等效二段线使新替代声速剖面与原始声速剖面间的净面积差为最小值时,计算新的i层上端点等效面积差ΔSCA和下端点的等效面积差ΔSCB。

(4) 保留最优替代端点。提取两端点所得的数据进行判断,若ΔSCA≤ΔSCB,用新替代的上端点DDi替代原始替代声速剖面上端点Di;若SCA>SCB,用新替代的下端点DDi+1替代原始替代声速剖面下端点Di+1。

(5) 输出数据。输出优化后新i层的声速替代剖面。

2 试验及分析

2.1 阈值的选取

阈值是简化模型中重要的参数指标,为确定阈值的影响,对一段声速剖面分别设定阈值为0.1、0.2、0.3、0.5、1、2 m/s,其替代优化分层效果如图6所示,图7记录不同阈值影响下的精简率和运算时间关系曲线。由图6、图7可以看出,当阈值设定为0.1和0.2 m/s时,两种方法的精简率是相同的,但本文方法会对一些声速剖面简化特征点进行改动;当阈值设定为0.3和0.5 m/s时,本文方法相较于MOV算法不仅对一些特征点进行改动,还增加了一些特征点;当阈值设定为1和2 m/s时,MOV算法对声速剖面的精简替代表现较差,虽然精简率较高但是不能很好地表现出声速剖面的特征,本文方法在这方面表现较好。

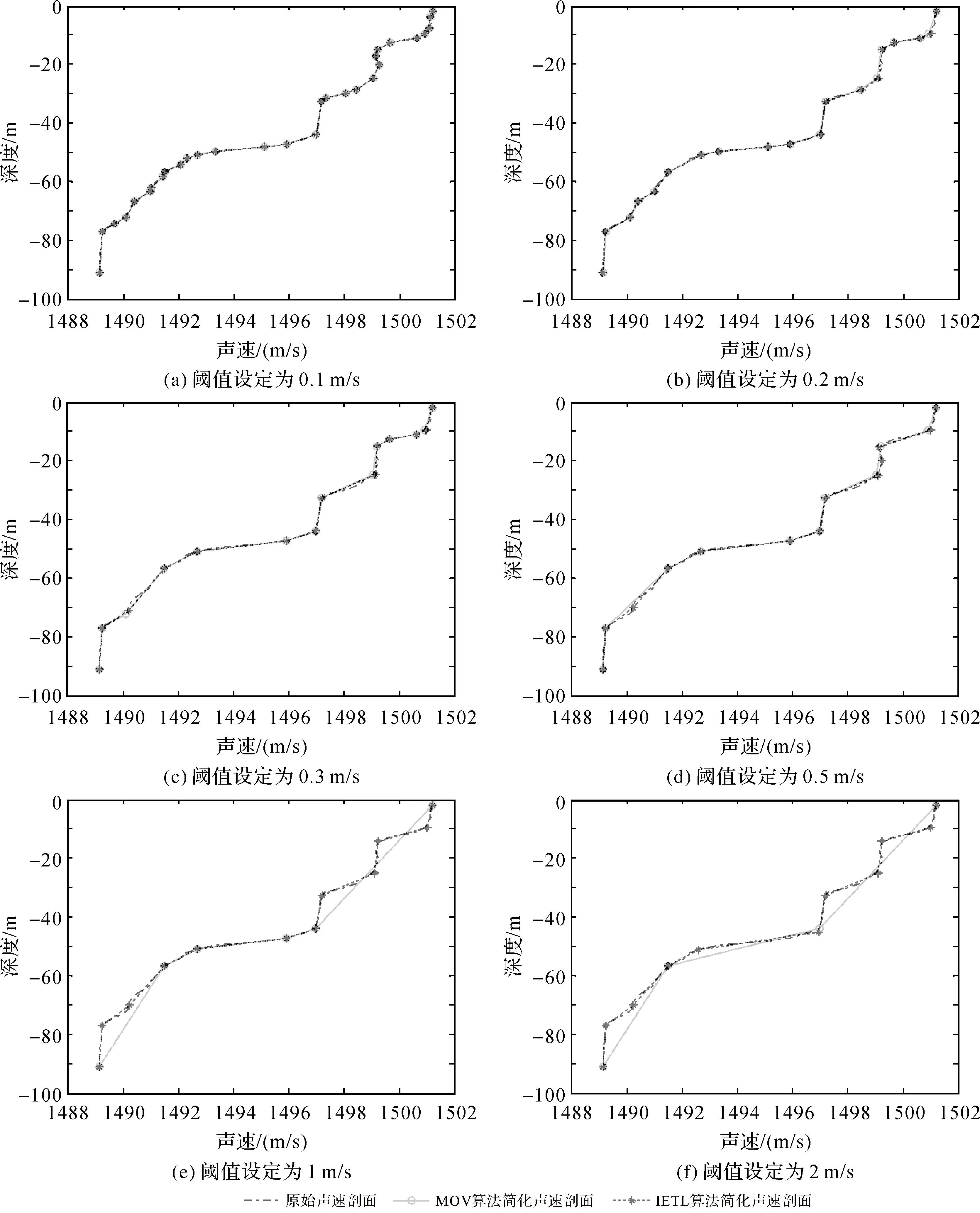
图6 设定不同阈值的简化声速剖面效果图对比Fig.6 Comparison of SVP renderings with different thresholds

图7 不同阈值影响下的精简率和运算时间关系曲线Fig.7 Relationship curves of reduction rate and operation time under different thresholds

由图7可以明显看出,本文方法相较于MOV算法计算时间较长,这是由于两种方法从计算模型角度出发,MOV算法只需提取每个采样点最大偏移量进行分析,而本文方法中多重循环嵌套明显在计算量方面要比MOV算法大得多,因此在前期简化过程中尽量使用MOV算法。MOV算法设定的阈值大小会直接影响整体改进方法的计算效率,阈值过小会导致简化率降低,使得多波束测深系统计算深度时效率降低;阈值过大会使得MOV算法过早停止简化,增加改进方法简化计算,降低整体简化效率。为在分层精度为主的基础上兼顾计算效率,阈值范围选取在0.2～0.4 m/s这个范围最优,根据声速剖面波动程度可做适当调整。

2.2 实测数据应用分析

为验证本文方法的有效性,通过对东海某测量船作业的实测数据进行验证分析。首先提取该区域的声速剖面数据,并对其进行不同方法的简化,如图8所示。设定阈值为0.2 m/s,本文IETL方法能够将300个声速剖面采样点简化为15个,MOV算法能将其简化为13个。在简化率上MOV算法略胜一筹,然而由图8可以看出,其中一部分原始声速剖面和MOV算法简化的替代声速剖面间存在较明显的面积差。图8中A点为原始声速剖面和替代声速剖面的交点,根据1.1.3节推导,该点处二者面积差最大,并且使用MOV算法简化的声速剖面计算的水深数据与原始测深数据误差也较大。

图8 实测数据声速剖面不同简化效果对比Fig.8 Comparison of different simplification effects of measured data SVP

图9为使用不同替代声速剖面计算后的海底地形图,其中图9(a)、(b)分别为原始海底地形图和使用MOV算法替代声速剖面计算后的海底地形图,对比两图可以发现,在图9(b)中H、J、K3处深度差较为明显,其原因为在该深度附近的替代声速剖面等效面积差较大,导致计算后的深度存在误差。图9(c)为运用本文方法的替代声速剖面计算后的海底深度,与原始海底地形深度差较小。对比海底地形直观图不明显,为便于对比分析,对两种替代方法的误差进行统计如表1所示,图10为深度差与深度关系的散点分布图。由图10可知,MOV算法在深度-55 m附近与原始声速剖面间的深度差比较大,随着深度的增加,替代声速剖面与原始声速剖面间面积差逐渐缩小,深度差也随之缩小。本文IETL方法在该深度区间内,与原始声速剖面间面积差较小,因此应用效果要优于MOV算法。由表1可知,MOV算法虽然平均相对误差在1%以内,但是部分数据误差大于1%,而IETL方法能够将整体和部分测深数据误差都能控制在1%以内,满足国际海道测量组织对水深测量的标准,并且精度更高。

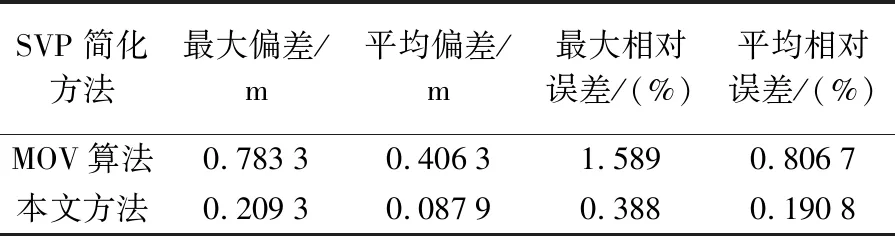
表1 不同SVP简化方法的误差统计

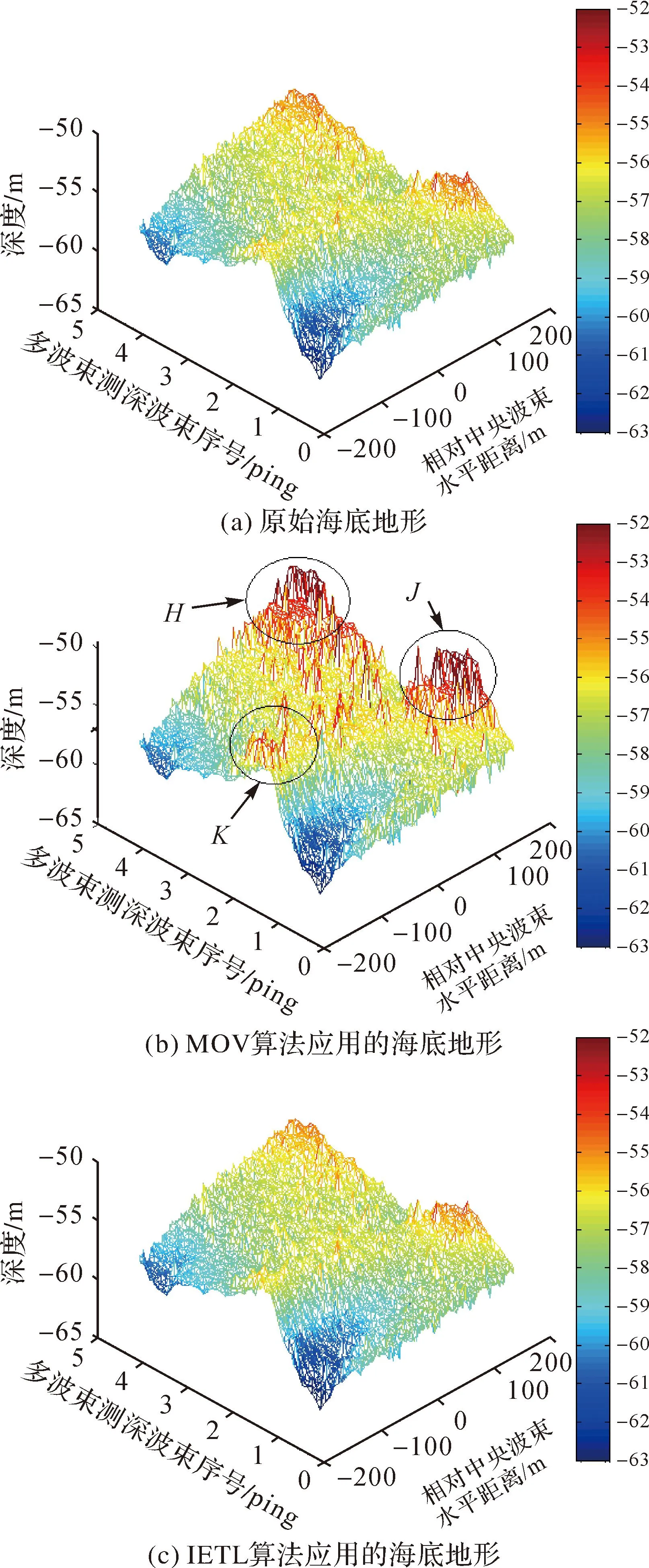
图9 应用不同简化声速剖面的实测海底地形Fig.9 Measured seabed topography using different simplified SVP

图10 应用不同简化声速剖面的深度差与深度关系散点分布Fig.10 Scatterplot of depth difference and depth relationship with different simplified SVP

3 结 论

本文提出了一种顾及面积差的声速剖面层内等效二段线替代法。该方法在MOV算法的基础上,针对其层间替代声速剖面不等效和精度不高的情况,通过构造最优的等效二段线来优化替代声速剖面。在原始声速剖面与替代声速剖面总体等效保证最低水深精度的同时,会出现由于部分层间声速剖面等效面积差较大,导致该水层替代声速剖面计算出深度精度较低。本文提出的IETL方法,适用于地形起伏较大的海底,此法在有效保留声速剖面弯曲特征点的同时,明显提高了层间声速数据的精度。

本文方法也存在一定问题,例如,为保证层间数据精度而在客观上牺牲了少量的精简率,并且该方法模型的计算要比MOV算法复杂,声速剖面简化提取特征点的计算时间也较长。因此,在地形起伏不大的区域,其应用优势不明显,并且在后续工作中需要对地形不同起伏程度的适应性,以及不同声速剖面等效面积差的影响效果进行进一步分析。