重定位非极大值抑制算法

苏树智，陈润斌，朱彦敏，蒋博文

（1. 安徽理工大学 计算机科学与工程学院，安徽 淮南 232001；2. 合肥综合性国家科学中心能源研究院（安徽省能源实验室），安徽 合肥 230031；3. 安徽理工大学 机械工程学院，安徽 淮南 232001）

1 引 言

目标检测［1］是计算机视觉的主要研究领域之一。它的任务是找出图像或视频中人们感兴趣的物体，并检测出它们的位置和大小。不同于图像分类［2］任务，目标检测不仅要解决分类问题，还要解决定位问题。此外，目标检测构成了许多其他计算机视觉任务的基础，例如实例分割［3］、图像标注［4］和目标跟踪［5］。自2014 年区域卷积网络目标检测算法［6］问世以来，基于卷积神经网络［7］的目标检测算法一直处于研究的前沿，相较于传统的目标检测算法，精度和速度都有了很大的提升。

基于卷积神经网络的目标检测算法［8-13］在预测阶段返回大量位置和尺寸不同的候选框，这些候选框大部分聚集在可能包含感兴趣目标的区域，对这些候选框执行保留和抑制操作很有必要。这些候选框只包含坐标与类别置信度信息。其中，坐标并不能作为决定最优边界框的依据，而类别置信度作为一个类别概率标签，用于表示候选框中存在某个类别物体的概率，类别置信度越高，候选框中存在某个类别物体的可能性越大。最优边界框的选定会影响后续的候选框抑制操作，如果不选择类别置信度得分最高的候选框而是选择其它候选框作为最优边界框，会导致类别置信度得分最高的候选框在候选框抑制阶段被移除，重复此操作，使得所保留的大部分最优边界框的定位精度较低，进而导致检测精度下降。因此，传统非极大值抑制（Non-Maximum Suppression，NMS）算法通常将类别置信度作为最优边界框的评价指标，对候选框按类别置信度降序排列［13］，并且选择类别置信度得分最高的候选框作为最优边界框［14-16］。然后，保留最优边界框并利用该框抑制与其交并比（Intersection over Union，IoU）大于一定阈值的候选框，如果在这些候选框中有多个对象存在，则选择剩余候选框中类别置信度最高的候选框作为下一个对象的最优边界框，并重复抑制过程，直到候选框全部被移除。传统NMS 算法仅依靠类别置信度选择最优候选框，导致其定位精度较差。类别置信度是一个类别概率标签，它和定位精度之间的相关性很低［17］，因此类别置信度并不能有效代表定位精度［18］。传统NMS算法使用它来决定最优边界框意味着很容易返回次优边界框。 虽然出现了很多改进算法［17，19-20］，但这些算法大部分需要在主干网络添加新的损失函数并重新训练目标检测模型，增加了时间成本。Jiang 等［17］提出在网络中添加预测分支来学习定位置信度，使用定位置信度作为最优候选框的筛选依据。He 等［15］提出在网络中添加边界框回归损失函数，用于学习边界框变换和定位置信度。

上述改进算法通过为每个候选框分配利用网络学习到的定位置信度来避免选择最优边界框时依赖类别置信度。传统NMS 算法认为与最优边界框重叠越大的候选框，越有可能是冗余框，因此，设定阈值用于判断候选框是否是冗余框。Liu 等［19］发现在不同的目标检测场景下设置不同的阈值能够提高召回率，提出了Adaptive-NMS 算法。Adaptive-NMS 算法通过在网络中添加密度预测模块来学习框的密度，根据图像中物体分布的稀疏程度确定阈值从而获得更高的召回率。Soft-NMS 算法［21］通过衰减而不是消除高度重叠边界框的类别置信度的策略，在一定程度上提高了召回率。但是上述算法的选框思想完全源自传统NMS 算法，即选择类别置信度得分最高的候选框为最优边界框，并不能从根本上解决所选最优边界框定位精度不高的问题。为了解决该问题，本文提出一种重定位非极大值抑制（Relocation Non-Maximum Suppression，RNMS）算法。该算法通过衡量边界框之间的距离，构建了一种利用最优边界框与其周围候选框之间的位置关系调整最优边界框位置的重定位选框法，在PASCAL VOC2012 和MS COCO2014 数据集上的实验表明，R-NMS 算法的mAP 相较于传统NMS 算法和Soft-NMS 算法有显著的提高。

2 相关工作

在目标检测任务中，通常使用传统NMS 算法和Soft-NMS 算法对预测阶段得到的候选框进行保留和抑制处理。

2.1 传统NMS

传统NMS 算法中，候选框抑制过程中类别置信度Sf的计算过程如下：

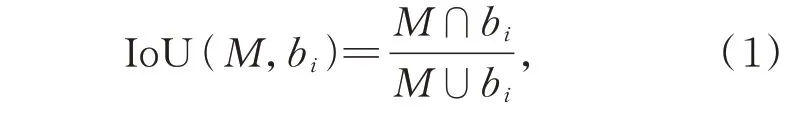
式中：M代表最优边界框，bi为候选框。IoU 用于衡量两个框之间的重合程度。

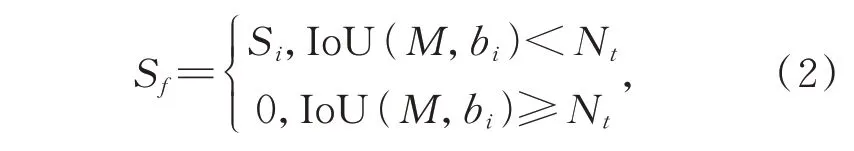
式中Nt为人工设定的阈值。当框M与bi框的重合程度大于N t时，bi框的类别置信度置为0，bi框被框M抑制。

2.2 Soft-NMS

Soft-NMS 算法是一种基于传统NMS 的改进算法。与传统NMS 算法相同，其候选框也根据类别置信度排序，置信度得分最高的候选框被选为最优边界框。不同于传统NMS 算法，Soft-NMS 算法采用“权值惩罚”的方式调整类别置信度，即：

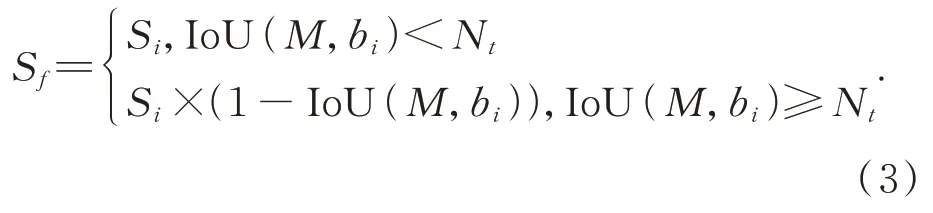
在Soft-NMS 算法中，与框M有显著重叠的候选框不会立即被移除，但是它们的置信度得分会衰减。这一方式有效地提高了召回率，但Soft-NMS 算法作为传统NMS 算法的改进算法，其选择最优边界框的思想完全继承了传统NMS 算法，不能从根本上解决所选最优边界框定位精度不高的问题。

3 R-NMS 算法

3.1 接近度P

曼哈顿距离是两点之间的垂直和水平距离之和，点u(x1，y1)和v(p1，q1)之间的曼哈顿距离HM(u，v)为：

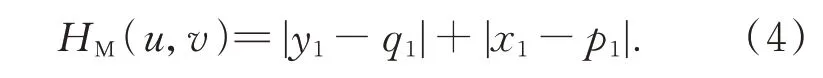
本文提出两个边界框之间的接近度P可以用 图1 中 点u(x1，y1)，v(p1，q1)之 间 的 曼 哈 顿 距离以及点m(x2，y2)，n(p2，q2)之间的曼哈顿距离之和表示：

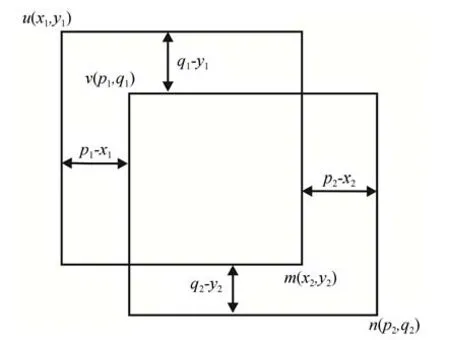
图1 曼哈顿距离Fig.1 Manhattan distance

接近度P和IoU 都能表示边界框之间的接近程度，然而P值随着重叠面积的改变呈现线性变化，如图2 所示。相比之下，IoU 的变化是非线性的，在一定程度上其阈值更加敏感。为了证明在衡量边界框之间的距离时P值优于IoU，4.2.2节对P和IoU 在R-NMS 算法上的性能进行了比较。

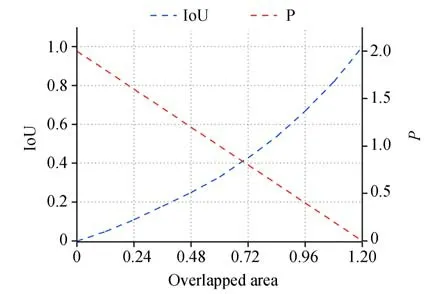
图2 P 和IoU 的 对 比Fig.2 Stability of P compared to IoU

3.2 坐标标准化

接近度P在边界框尺寸相似的情况下能够有效地表示边界框之间的距离关系。然而，在目标检测的后处理阶段存在大量尺寸不同的候选框，图3 在右侧显示了两个大边框，左侧有两个小框。对每组边框进行P值计算，得到：

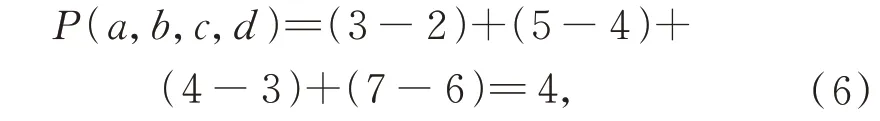
图3 两组框在坐标轴上的展示Fig.3 Display of two sets of boxes on coordinate axes

显然，当两个框的尺寸有明显差异时，P值并不能准确衡量它们的重合程度。为了解决这一问题，本文引入了边界框坐标点标准化这一方法，该方法能够使坐标被固定到0～1 之间，同时还能保持边界框之间的关系。坐标标准化公式如下：

式中：norm 用于坐标标准化，X，Y分别表示两个框的横坐标、纵坐标的集合，max(X)，min(X)表示两个框中横坐标的最大值和最小值。利用横坐标xi到最小值的距离比上最大值和最小值之间的距离即可得到标准化后的横坐标，纵坐标的标准化计算过程和横坐标的相同。对图3 中右侧的两个边界框的坐标执行标准化操作后，它们的边 界 框 坐 标 由u(10，2)，v(20，10)，m(9，3)，n(19，11) 变 换 为u(0.091，0)，v(1，0.899)，m(0，0.111)，n(0.909，1)。它们的P值利用式（8）计算后为0.404。同理，图中左侧边界框的坐标分 别 由a(2，4)，b(3，6)，c(3，5)，d(4，7) 转 为a(0，0)，b(0.5，0.667)，c(0.5，0.333)，d(1，1)，最终P值为1.666。显然，坐标标准化后两组边界框的P值不相同。因此，标准化坐标后计算得到的P值能够区分边界框的重合情况。

3.3 最优边界框重定位

传统NMS 和Soft-NMS 算法选取最优候选框的过程是一致的。首先，候选框按类别置信度降序排列，然后选择类别置信度得分最高的候选框为最优边界框。然而，候选框的定位精度和类别置信度之间的相关性不大，类别置信度得分最高的候选框不一定是最优边界框。为此，RNMS 算法在得到最优边界框的基础之上，利用重定位选框法对它执行重定位操作，重定位过程如图4 所示。第一步，找到与最优边界框的接近度P小于阈值（阈值取值在0～1.0，取0.3～0.5最佳）的候选框；第二步，计算最优边界框和符合第一步要求的候选框之间的平均偏移量；第三步，最优边界框利用第二步获取到偏移量进行重定位。计算过程如下：

图4 边界框重定位流程Fig.4 Process of relocating bounding boxes

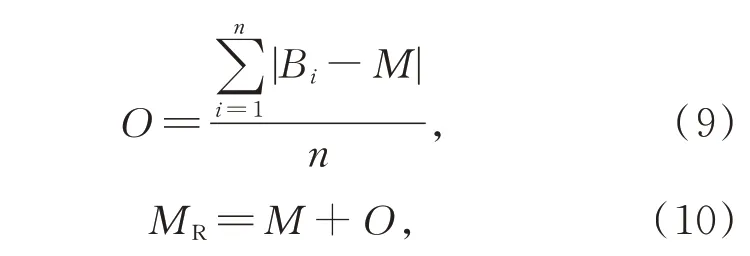
式中：B为符合条件的候选框集合，Bi为候选框，O为B中所有候选框与最优边界框M的偏移量。最优边界框M加上偏移量O即可得到R-NMS 算法的最优边界框MR。

3.4 边界框的保留和抑制

在模型预测阶段，同一个目标上会产生大量相似的候选框，存在大量的冗余数据，因此边界框的保留和抑制至关重要。在对这些边界框进行处理时，首先根据类别置信度对候选框排序，选择得分最高的候选框作为最优边界框，然后借助重定位选框法对最优边界框执行重定位操作得到新的最优边界框。最后，采用最优边界框抑制其他候选框。图5 中，左图的红框为借助重定位选框法得到的最优边界框，利用该最优边界框抑制蓝色的候选框，最终只保留红色边界框（彩图见期刊电子版）。

图5 边界框的保留与抑制过程Fig.5 Process of reserving and suppressing bounding boxes

R-NMS 算法的执行步骤如下：

4 实验分析与讨论

4.1 实验数据、模型及参数

本文的实验建立在公开可用的MS COCO2014 和PASCAL VOC2012 数据集上。MS COCO2014 数据集共有80 个类、164 042 张图片，可分为训练集、验证集和测试集，分别有82 783，40 504，40 755 张 图 片。在PASCAL VOC2012中训练、测试及验证数据集共包含17 125 幅图像，20 个类。这些数据集用于训练和评估深度学习目标检测模型。

实验选用pytorch 框架，使用python3.8 编程，硬件设备中CPU 使用AMD Ryzen 9 3900X，内存为32 GB，GPU 型号为GeForce RTX 2080Ti，显存为11 GB，系统环境为Ubuntu18.04。使用目标检测器YOLOv3、YOLOv5以及Faster RCNN 对传统NMS，Soft-NMS 和RNMS 算法的性能进行了比较评估。实验过程中，类别置信度的阈值设为0.2，IoU 的阈值和接近度P的阈值都设为0.5。

4.2 实验结果

4.2.1 R-NMS 算法和其他算法的性能对比

利用YOLOv3，YOLOv5 以及Faster RCNN算法在PASCAL VOC2012 和MS COCO2014测试集上比较了传统NMS，Soft-NMS 和RNMS 的性能，结果如表1～表2 所示。与传统NMS 相比，使用Soft-NMS 作为目标检测任务的后处理算法时，在抑制边界框阶段对冗余边界框的类别置信度得分采取了“权值惩罚”策略，一定程度上减少了目标漏检，使得召回率有所提高，但是同时带来了目标重复检测问题，如图6～图7所示，部分目标被重复检测。重复检测导致精确率下降。在PASCAL VOC2012 测试集上，YOLOv3 算法的精确率由80.6%降至80.3%，YOLOv5 算法的精确率降低了0.1%。在MS COCO2014 测 试 集 上，YOLOv3 算 法 和YOLOv5 算法的精确率都有所下降。

图6 YOLOv3 算法在VOC 数据集上的部分检测结果Fig.6 Experimental results of VOC test dataset on YOLOv3

图7 YOLOv3 算法在COCO 数据集上的部分检测结果Fig.7 Partial experimental results of COCO test dataset on YOLOv3

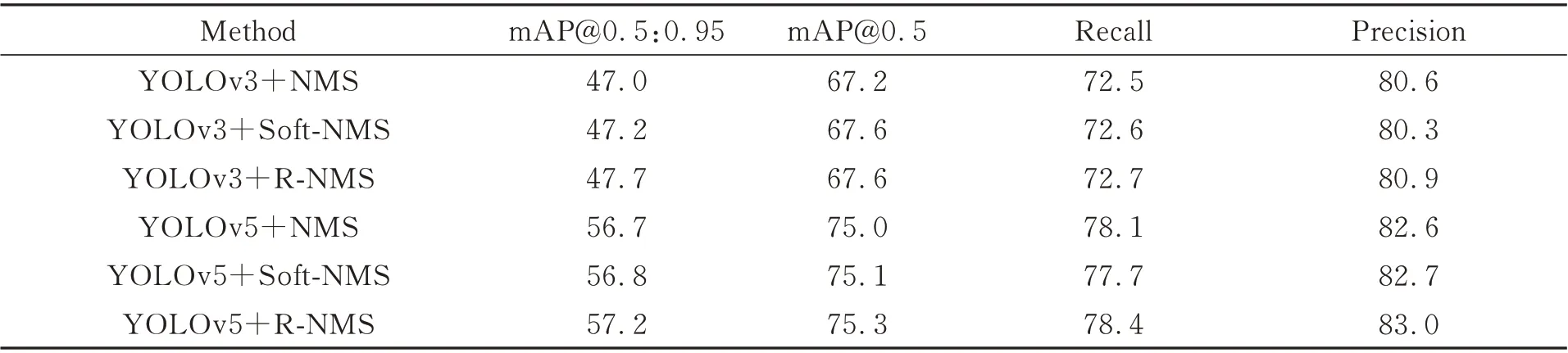
表1 三种不同NMS 算法在VOC 数据集上的实验结果Tab.1 Experimental results of three different NMS algorithms on VOC test dataset （%）

表2 三种不同NMS 算法在COCO 数据集上的实验结果Tab.2 Experimental results of three different NMS algorithms on COCO test dataset （%）

本文提出的R-NMS 算法，在传统NMS 和Soft-NMS 算法所选的最优边界框基础上充分利用其周围框的位置信息，对最优边界框执行重定位，最终获取到定位精确的最优边界框。在PASCAL VOC2012 测试集上，R-NMS 作为YOLOv3 和YOLOv5 算 法的后处理算法，R-NMS 算法的精确率高于传统NMS 算法的80.6%，82.6%，R-NMS 算法的召回率也从Soft-NMS 算法的72.6%，77.7% 提升至72.9%，78.3%。YOLOv3 算法的mAP@0.5：0.95 指标分别提升了0.7%，0.5%。YOLOv5 算法的mAP@0.5∶0.95 由 传 统NMS 算 法 的56.7%，Soft-NMS 的56.8% 提升至R-NMS 的57.2%。在MS COCO2014 测 试 集 上，YOLOv3 和YOLOv5 的 实 验结果如表2 所示。R-NMS 算法的mAP@0.5∶0.95 指标都优于传统NMS 算法和Soft-NMS 算法，召回率和精确率同上。在此基础之上，对3 种非极大值抑制算法在PASCAL VOC2012 测试集的实验结果进行了展示，如图6～图7 所示，图中传统NMS 和Soft-NMS 算法所选的最优边界框经过R-NMS 算法的重定位选框法处理后定位精度得到提升。图6 和图7 只选取了部分检测结果，利用R-NMS 算法得到的最优边界框能准确地包围目标，传统NMS，Soft-NMS 算法与之相比存在明显的差距。图8 展示了Faster RCNN 算法在PASCAL VOC 2012测试集上的部分实验结果，在mAP 这一指标上R-NMS 算法相较于传统NMS，Soft-NMS算法分别提高了0.53%，0.36%。

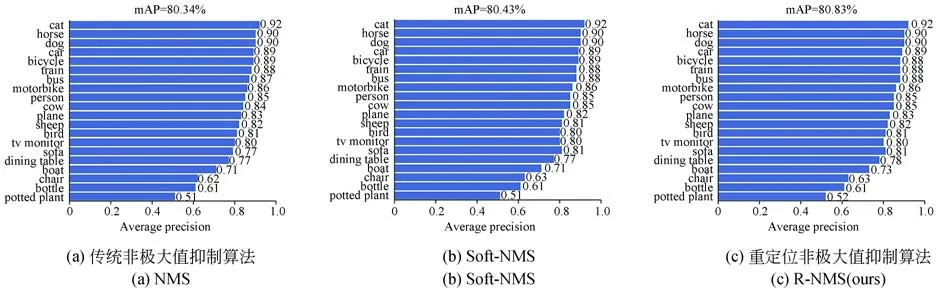
图8 Faster RCNN 算法在PASCAL VOC 上的实验结果Fig.8 Experimental results of VOC test dataset on Faster RCNN

以上实验结果证明了R-NMS 算法的性能优于传统NMS 和Soft-NMS 算法。相比传统NMS算法和Soft-NMS 算法，R-NMS 算法不仅解决了传统NMS 算法召回率低的问题，还提高了精确率。

4.2.2 接近度P和IoU 的消融实验

本节比较了在R-NMS 算法上IoU 和接近度P的性能。实验建立在PASCAL VOC2012 数据集上，实验结果如表3 所示，接近度P在R-NMS算法上的各个性能评价指标上的表现均优于IoU。因此，当最优边界框周围存在大量候选框时，接近度P能够帮助R-NMS 算法选取更加合适的候选框用于后续重定位操作。

表3 P 和IoU 在R-NMS 算法上的实验对比Tab.3 Experimental results of R-NMS with P or IoU （%）

4.2.3 R-NMS 算法的阈值敏感性分析

实验中使用YOLOv3 检测器和PASCAL VOC2012 测 试 集，对R-NMS 算 法 中 接 近 度P的阈值进行了敏感性分析。图9 展示了接近度P的阈值分别为0.5，1.0 时最优边界框及其周围候选框的位置信息（彩图见期刊电子版），左图的绿框代表最优边界框，红框代表最优边界框周围接近度P小于阈值的候选框，右图绿框表示利用重定位选框法得到的最优边界框。当接近度P的阈值 为0.5 时，图10 中R-NMS 算 法 的mAP 由67.2%提高到67.6%，此时最优边界框周围的候选框数量较少但定位精度较高，利用它们的位置信息能够提高最优边界框对物体的包围程度。因此，图9（a）右图中最优边界框的定位精度相较于左图有所提升。当接近度P的阈值为1.0 时，最优边界框周围候选框的数量增多，但是这些新增候选框远离最优边界框并且包围物体的程度较低，利用该位置信息对最优边界框重定位会导致定位精度下降。 此时，R-NMS 算法在VOC2012 测试集上的mAP 下降至67%，低于传统NMS 算法的67.2%。

图9 不同接近度阈值下的最优边界框Fig.9 Optimal bounding box with different proximity thresholds

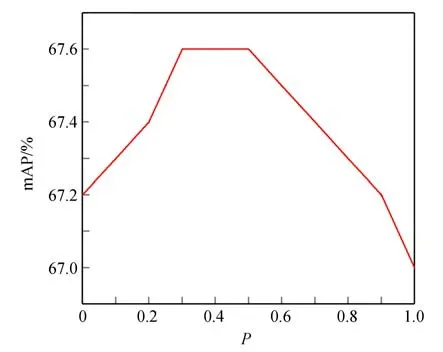
图10 接近度的阈值敏感性分析Fig.10 Threshold sensitivity analysis of proximity

当接近度P的阈值较低时，最优边界框能够利用的有效位置信息较多，使得重定位选框法得到的最优边界框包围物体的程度提高。随着阈值的提高，最优边界框获得更多周围候选框的位置信息，但是这些位置信息无效并且会降低最优边界框的定位精度。由此可知，R-NM 法的性能在阈值较低时能够获得更好的性能。

4.3 定性分析

传统NMS 算法和Soft-NMS 算法选择类别置信度最高的候选框作为最优边界框，然后借助该框抑制任何与其高度重合的候选框，从而完成候选框的保留与抑制。但是在实验中发现，类别置信度和定位之间的相关性不高，有时候置信度低的边界框能更好地包围目标。图11 中左侧的检测结果来自传统NMS 算法，而右侧的检测结果来自实验。传统NMS 算法只是简单地返回类别置信度最高的边界框，即使该边界框不是很准确，忽略了类别置信度得分和定位精度之间的相关性很小。在传统NMS 算法的处理下，包围骑手的边界框的类别置信度为0.48。但是候选框集合中存在另外一个能够将骑手包围的候选框，而该候选框的类别置信度只有0.40。显然，传统NMS 算法只选择了类别置信度得分最高的候选框为最优边界框，而置信度得分较低但是能够精确包围目标的候选框却被丢弃。本文提出的RNMS 算法充分考虑到最优边界框周围存在类别置信度得分较低但是与最优边界框重合程度较高的候选框，充分利用它们的位置信息并融合到最优边界框，就能得到定位更加准确的最优边界框。上述实验证明了R-NMS 算法的有效性，利用R-NMS 算法处理得到的最优边界框与真实框的重合程度更高，因此R-NMS 算法相较于传统NMS，Soft-NMS 算法，所有评价指标都有明显的提升。

图11 定位精度和置信度的关系Fig.11 Relationship between classification confidence and positioning accuracy

5 结 论

传统NMS 算法及其变体Soft-NMS 算法在选框阶段根据类别置信度选出最优边界框，而定位精度和类别置信度之间的相关性很低，类别置信度得分最高的候选框的不一定是最优边界框。针对上述问题，本文提出R-NMS 算法。该算法综合考虑最优边界框与其周围候选框的位置信息，构建了一种重定位选框法，最优边界框可以借助该方法重新调整位置，最终提高其定位精度。实验结果证明：采用PASCAL VOC2012 数据集测试，与传统NMS 算法和Soft-NMS 算法相比，R-NMS 算法在目标检测器YOLOv3 上的mAP 分 别 提 高0.7%，0.5%，R-NMS 算 法 在Faster-RCNN 上的mAP 达到80.83%。该算法能提高目标检测器的检测精度。