基于量子海鸥算法的运载火箭回收舱段时差定位方法
2024-01-08叶智慧吴红梅董志源
叶智慧,吴红梅,王 佩,熊 伟,郭 颖,陈 略,董志源
(1.西北工业大学 航天学院,陕西 西安 710072;2.上海航天电子技术研究所,上海 201109;3.北京航天飞行控制中心,北京 100094)
0 引言
近年来,航天发射任务日益增加,运载火箭可重复使用发射技术是低成本进入空间的重点发展方向,得到了各航天强国的高度重视[1-2]。随着Space X可重复使用火箭的多次发射试验成功,运载火箭重复使用技术再次受到航天业的高度重视,成为航天技术的热点之一。现有火箭子级舱段回收面临着陆区域范围广、受地形影响大、特殊任务下回收时间窗口有限等问题,对运载火箭回收舱段持续准确定位是解决上述问题的关键[3-4]。通过对弹箭持续准确定位可以获得弹箭飞行轨迹,为弹箭飞行测试、故障排除提供原始数据。因此,发展作用距离远、电磁辐射隐蔽性强、高效定位技术势在必行。本文针对运载火箭回收舱段定位问题展开研究,基于海鸥算法(Seagull Optimization Algorithm,SOA)和达到时间差(Time Difference of Arrival,TDOA)定位原理对火箭子级舱段位置进行定位解算。
TDOA 技术是无源定位中广泛应用的方法之一,具有硬件要求不高、算法复杂度低、对时间戳无特定要求、定位精度较高等优势,并且常用与测角、频差等无源定位体制相结合形成联合定位算法[5-6],具有融合度高、适配性强的特点。目前TDOA 定位解算方法主要有解析法和优化法两类。其中解析法主要由泰勒级数展开法和最小二乘法组成。泰勒级数法通过有限阶次展开后的迭代计算来实现目标位置的估计,主要缺点是受迭代初值影响很大,初值估计不准甚至会导致迭代计算不收敛,这极大的限制了泰勒级数法的使用[7-8]。最小二乘法具有不迭代、速度快、计算量小等特点,在噪声不大的情况下具有较高定位精度。许多学者在此基础上开展进一步研究,通过增加约束条件,将最小二乘问题转化为凸优化问题进行求解,产生了约束最小二乘法,提高了定位精度。但最小二乘法在使用时不可避免地存在矩阵求逆,为保证矩阵不出现奇异导致对观测站数量提出了更多的要求,对于3 维定位场景,为保证精度至少需要设置5 个观测站。此外,最小二乘法应用的前提是观测误差较小,随着观测误差增大定位精度将急剧下降[9-12]。
借鉴最小二乘法将定位问题转化为优化问题的思想,近年来不断有学者将智能优化算法应用于TDOA 无源定位解算。2010 年WEI 等[13]在Kenneth 采用粒子算法解决时差定位问题的基础上,利用改进的自适应粒子群算法进一步提升了定位精度[14]。2017 年刘宝生[15]将遗传算法应用于时差定位解算同样取得了更高的定位精度。2018 年,陈涛等[16]将樽海鞘算法用于3 维时差定位解算,通过改进算法提升了算法的性能和精度,减少了控制参数。2022 年,陈光武等[17]改进鲸鱼优化算法进行时差定位非线性方程求解提高了定位精度和收敛速度。相比传统解析法,智能优化算法通过构建与测量值相关的适应度函数来评价大量随机点与真值的相似度,利用智能优化算法的迭代逼近能力获得最佳的目标位置估值,由于该方法无需求逆,对初值和测量噪声不敏感,对测量站数量少,随着计算能力的飞速发展,相比解析法的优势日益凸显。基于智能优化算法的TDOA 求解方法的主要问题在于智能优化算法本身普遍存在后期收敛速度慢,存在早熟问题和全局最优解求解精度不高等缺陷。部分算法控制参数多导致时差定位精度受参数影响很大。因此,探索和改进新型智能优化算法并应用于时差定位具有很好的现实意义和应用价值。
2019 年,DHIMAN 等[18]通过观察海鸥的迁徙和攻击行为,提出SOA,该算法步骤简单、控制参数少,求解稳定性方面相比其他群集智能优化算法有一定优势。本文将量子计算与海鸥优化算法结合,将量子海鸥优化算法(Quantum Seagull Optimization Algorithm,QSOA)应用于运载火箭回收舱段的三维时差定位解算,并对Chan 算法和传统SOA 进行比较。
1 运载火箭回收舱段时差定位系统设计
目前常用的多站无源定位方法按照测量量可以分为基于时间、基于角度和基于频率3 种。基于角度信息的到达角定位技术,根据各基站与定位信号源之间方位线的交点来确定信号源位置,该方法具有距离依赖性高、定位精度差的缺点[19]。基于频率的多普勒频差定位方法根据定位信号源达到各基站的多普勒频率进行定位,存在测量误差大、定位模糊等问题,一般难以单独使用[20-22]。而基于时间信息的达到时间差定位方法,利用信号源发射信号达到各基站的时间差进行位置解算,具有独立性强、设备简单、探测范围大、定位实时性强等优点,在无源定位领域广泛应用。因此,本文采用TDOA 定位方法设计运载火箭回收舱段时差定位系统,该系统由4 个地面基站组成,1 个主站3 个辅站,在回收舱段上安装信号发射装置,主站定时向3 个辅站发送同步信号,主站将各站接收到辐射源信号的时间戳收集后进行TDOA 定位解算。设主站的位置为(x1,y1,z1) 和各辅站的位置为(xi,yi,zi)(i=2,3,4),火箭回收舱段的位置为X=(x,y,z)。整个定位系统如图1 所示,计算主站与各辅站之间的时间差t1i,i=2,3,4,联立时间差非线性方程组对目标位置进行解算。由于各基站与主站不可能完全同步,因此时间差的测量量不可避免的含有误差,根据时间差获得的火箭回收舱段到主站与各基站之间的相对距离称为伪距。基于TDOA 原理,建立如图1 所示的火箭回收舱段定位系统。
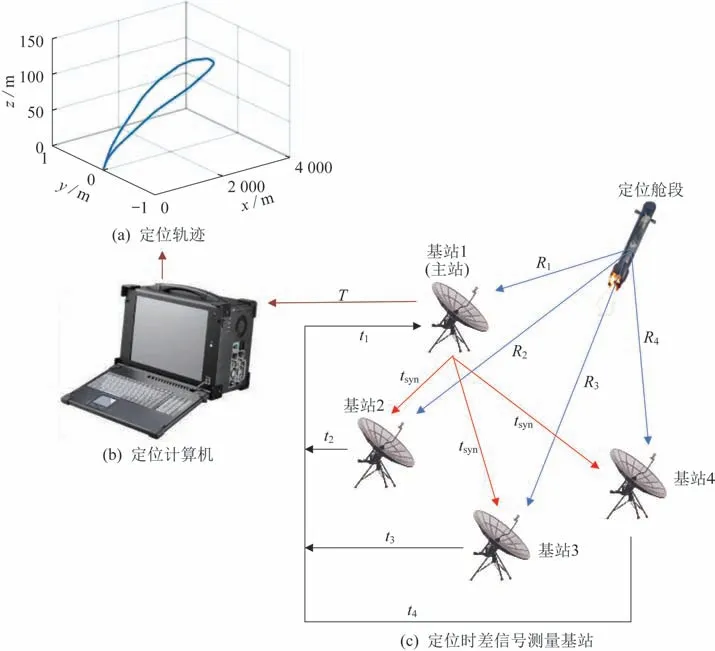
图1 基于到达时间差的运载火箭回收舱段定位系统Fig.1 Positioning system of a launch vehicle recovery cabin based on the TDOA
式中:R1为运载火箭回收舱到主站的距离;Ri为运载火箭回收舱到各辅站的距离;c为光速;t1为主站收到运载火箭回收舱发射信号的到达时间;ti为各测量辅站收到运载火箭回收舱发射信号的到达时间;Δti为主站和辅站收到运载火箭回收舱发射信号的到达时间之差。
考虑到达时间差测量值受到同步、传输等误差因素的影响,TDOA 测量值可表示为
式中,eri为主站与第i个辅站之间到达时间差的测量误差,一般可以认为其服从均值为0,方差为的高斯分布。
在基站数量N大于3 的情况下,可以采用最大似然法对火箭回收舱段的位置坐标进行估计,假设回收舱段的位置估计值为(,,)。考虑到Δtci服从高斯分布,且均值为t1-ti,方差为。假设各辅站测量数据是独立不相互影响的,则可建立如下的似然函数来表示各到达时间差之间的相互关系:
这样就将回收舱段的位置估计问题转化为使似然函数的最大值求解问题,即:
为求解使似然函数最大的火箭回收舱段坐标值,可以将式(4)转化为
如果根据式(5)定义优化问题的适应度函数f(X)为
则可以将回收舱段位置解算问题转换为使适应度函数fitness()最小的优化问题,从而解决了式(1)非线性方程的求解困难的问题。
2 海鸥算法
SOA 是模拟海鸥的迁徙和攻击行为的仿生优化算法,其中迁徙行为用于实现优化变量由当前位置向更优位置移动,而攻击行为用于局部搜索。
2.1 迁移行为
海鸥的迁移行为控制海鸥个体由当前位置向更优的位置移动。在海鸥迁移时应考虑避免相互之间碰撞,然后引导海鸥向当前海鸥个体最佳位置靠拢。为了避免碰撞发生,采用动态权重A计算海鸥的新位置。
式中:l为迭代次数;CS(l)为与其他海鸥不发生碰撞的新位置;PS(l)为海鸥移动前的位置;Ntmax为最大迭代次数。动态权重A由fc控制,随着迭代次数的增加将线性衰减到0。
在避免了碰撞之后,控制海鸥向当前海鸥个体所在最佳位置移动。
式中:MS(l)为海鸥向当前海鸥个体最佳位置移动的方向;B为折衷随机数用于平衡全局和局部搜素,rd为[0,1]范围内的随机数。
在计算出每个海鸥的最佳移动方向后,海鸥先移动到避免碰撞的位置后,就向着当前最佳位置方向进行移动,达到新的位置DS(l)。
2.2 攻击行为
海鸥在迁徙过程中可以不断改变攻击角度和速度,它们用翅膀和重量保持高度。当攻击猎物时,海鸥们就在空中进行螺旋形状运动。wx、wy和wz平面中的运动行为描述如下:
式中:r为每个螺旋的半径;θ为[0,2π]范围内的随机角度值;u、v为螺旋形状的相关常数。
海鸥的攻击位置PS(l)由下式确定:
2.3 算法步骤
SOA 算法的计算步骤为:
步骤1海鸥群初始化,设置算法参数fc、u和v,最大迭代次数Lmax;
步骤2计算每个海鸥个体的适应度函数;
步骤3按照迁移行为和攻击行为更新每个海鸥个体的位置;
步骤4根据每个海鸥个体的新位置更新最佳位置和适应度函数值;
步骤5如果达到最大迭代次数,跳转到步骤6,否者跳转至步骤3;
步骤6输出最佳海鸥个体位置和适应度函数值。
3 量子海鸥算法(QSOA)
标准海鸥算法虽然控制参数少、步骤简单,但在平衡全局和局部搜索能力方面,存在容易陷入局部最优、算法收敛性差等问题。国内外学者不断尝试对标准海鸥算法进行改进,HU 等[23]采用变异和对立学习策略增强海鸥算法跳出局部极值的能力,CHE 等[24]将鲸鱼算法的包围策略与海鸥攻击行为相结合,改善海鸥算法局部能力。针对迁徙阶段固定惯性参数带来的算法初期全局寻优能力有限,容易陷入局部极值的问题,秦维娜等[25]引入非线性惯性权重策略控制迁移阶段收敛速度,加入levy 飞行增强算法跳出局部极值的能力,改善了算法的全局和局部搜索的均衡性。针对算法收敛精度差的问题,上述改进方法分别从不同角度出发对海鸥算法的搜索平衡性、收敛速度和寻优精度进行了改善。综上所述,制约海鸥算法寻优能力的关键是保证算法多样性的能力,提升迭代过程对寻优参数空间的覆盖均匀性,同时在进行局部搜索时,保持算法跳出局部最优的能力。因此,有必要从算法初始化、算法搜索前期和算法收敛后期均进行相应的改进,始终维持算法多样性和跳出局部极值的能力。为此,本文将量子计算和混沌理论与SOA 相结合,提出QSOA,基于量子编码表征个体位置,通过正余弦位置的差异性始终维持对参数空间覆盖的多样性,提高算法搜索效率。在算法初始化阶段通过混沌映射增强初始海鸥个体位置散布的均匀性,进一步提高算法初期的全局搜索能力,通过变异反向学习机制使算法具备跳出局部极值的能力。具体算法由个体编码、混沌映射初始化、搜索更新、变异反向学习处理4 个部分组成,下面分别进行介绍。
3.1 基于量子编码和Bernoulli 混沌映射的海鸥位置
在QSOA 中,海鸥的位置由量子编码的概率幅表示。假设海鸥种群规模为m,待优化变量的维数为n,则第l代海鸥种群所在位置为P(l)=[SQ1(l),SQ2(l),…,SQm(l)],第i只海鸥的位置由量子编码表示为
式中:θij=2παij为基于Bernoulli 混沌映射随机数αij生成的量子幅角,i=1,2,…,m,j=1,2,…,n;m为种群规模;n为优化变量空间维数。
每个海鸥状态占据参数解空间中的两个位置,分别对应量子态|0和|1的概率幅。即
式中:SQic(l)为余弦海鸥位置;SQis(l)为正弦海鸥位置。
式中:rd为(0,1)之间的随机数。
通过增加混沌映射提高海鸥种群初始化的搜索空间遍历均匀性、随机性,从而改进依靠随机生成的种群多样性难以保证、算法寻优结果差的问题。
图2(a)和图2(b)分别给出了在二维空间中,传统随机初始化和利用Bernoulli 混沌映射初始化的种群初始值分布图,图2(a)中种群在参数空间中散布并不均匀,部分区域分布较为密集,在左上角、右上角及中间区域则较为稀疏,而图2(b)中种群在整个空间内分布则较为均匀。从两种初始化策略的种群取值直方图,由图2(c)~图2(f)可知,采用Bernoulli 混沌映射初始化的种群在取值上更加均匀,这样可以改善传统初始化策略由于海鸥种群初始化时空间分布不均匀,导致算法早熟,容易陷入局部最优解的问题。

图2 两种初始化策略种群分布对比Fig.2 Comparison of the population distributions of two initialization strategies
3.2 量子海鸥个体搜索
采用量子编码的海鸥个体位置需要先转换为数值位置向量后对才能用于计算适应度函数,由适应度函数值评价每只海鸥所在量子位置的好坏。因此,需要通过量子搜索完成量子海鸥个体向优化参数解空间的数值转换。采用量子编码后每只海鸥所在位置可代表实际优化参数空间中的两个位置,分别对应量子态|0和|1的概率幅,设海鸥当前量子状态SQi(l)上的第k个量子位可表示为,则相应的解空间中对应的正弦、余弦位置变量XQij,j=c,s表示为
通过适应度函数f(X)计算当前量子状态SQi对应的每个解空间位置坐标XQij,j=c,s的适应度函数值,取最小值作为当前量子海鸥位置的量子适应度值F(SQi(l))。
当所有海鸥个体搜索完后,根据每只量子海鸥当前位置的量子适应度函数值F(SQi(l))选择出从迭代开始到当前代的最小值YBest(l),即
记录其对应的量子海鸥所在位置作为最优位置XBest。
3.3 QSOA 位置更新机制
海鸥的位置更新由量子迁移、量子攻击和变异及反向学习行为3 部分组成。
1)量子迁徙位置更新
在量子计算中量子的移动由量子旋转门实现,因此采用量子旋转门转角的更新方式来移动量子海鸥的位置。参考标准迁徙行为,使用动态权重A来计算量子海鸥的新量子幅角。
式中:θCij(l+1)为新位置幅角;θij(l)为第i只量子海鸥个体第j位当前位置幅角;l为当前迭代次数;动态权重A计算方法保持不变。
旋转到新幅角之后,量子海鸥向种群中最佳幅角所在的方向旋转。
式中:θMij(l+1)为向当前最佳量子海鸥位置第j个幅角旋转的角度;θbj(l)为最优量子海鸥位置的第j位的幅角;B计算方法保持不变。
每只量子海鸥通过自身随机旋转以及面向最优幅角的两种旋转移动方式,到达新幅角θDij(l+1),实现量子迁移行为。
2)量子攻击位置更新
量子海鸥在迁徙过程中还可以不断改变攻击角度和速度,在空中进行螺旋形状运动。在wx、wy和wz平面中的运动行为描述如下:
式中:β为[0,2π]范围内的随机角度值。
量子海鸥的量子位幅角在通过攻击算子旋转到新角度θij(l+1)。
更新后量子海鸥SQi(l+1)将表示两个新位置为
量子旋转门通过改变海鸥的量子幅角,对量子海鸥状态所代表的两个设计空间位置进行同步更新,在种群规模不变的情况下,扩展了对搜索空间的遍历性,提高了单次更新的搜索效率。
3)变异及反向学习行为
标准海鸥算法中没有对海鸥位置进行较大范围的干扰,使得算法随着迭代次数的增加种群内部多样性减少,陷入局部最优的概率增大。为此借鉴遗传算法中的变异操作,通过量子非门实现量子海鸥算法的变异处理,从而保持种群的多样性,避免早熟收敛。设置变异概率Pm,对每只海鸥个体抽取随机数rd判断该个体是否发生变异。若Pm>rd则变异发生,采用量子非门改变该位置的幅角得到变异幅角(l+1)。反向学习(Opposition-Based Learning,OBL)是通过估计和比较可行解及反向解来提高单步执行效率的方式,有助于提升种群的多样性。将变异概率和反向学习相结合,量子海鸥的变异反向学习行为表达式为
式中:POBL为反向学习概率;rd()服从[0,1]均匀分布的随机数。
4 基于QSOA 的运载火箭回收舱段无源时差定位算法
在运载火箭回收舱段定位问题中,舱段受环境、外界干扰影响运动范围很大。为了保证优化算法的全局性、多样性和求解稳定性,提出了量子海鸥算法,使用QSOA 进行火箭回收舱段TDOA 定位的具体步骤如图3 所示,具体如下:

图3 基于量子海鸥算法的运载火箭回收舱段TDOA 定位解算流程Fig.3 Process of the TDOA positioning for the launch vehicle recovery cabin based on the QSOA
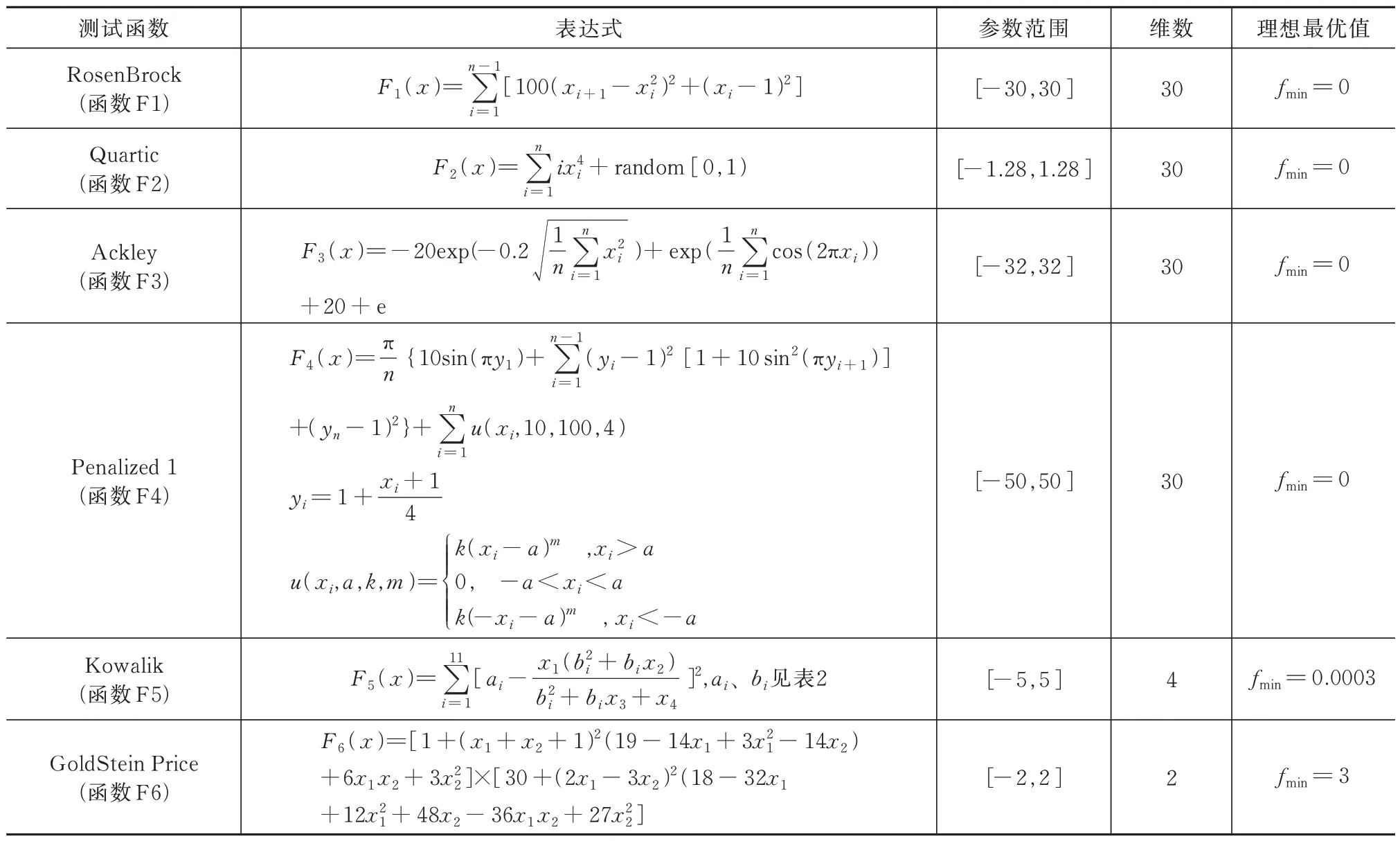
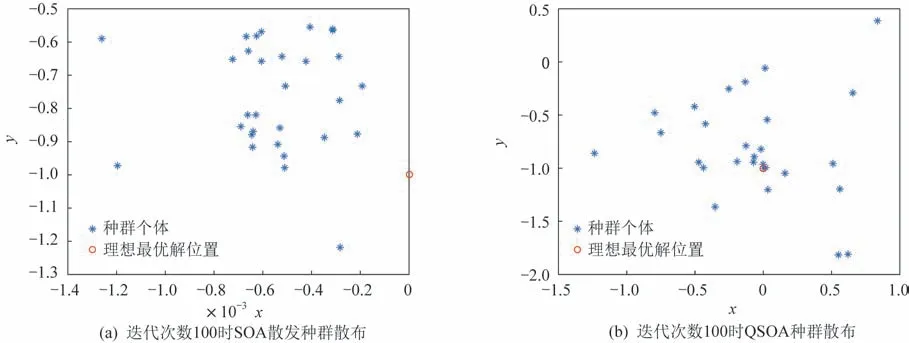
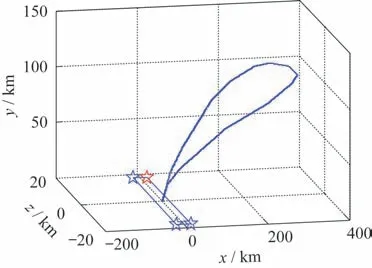
1)算法参数设置,设计变量的寻优范围[Lbk,Hbk],k=1,2,…,n,n是设计变量空间维数,对于三维定位问题n=3,Lbk为第k个设计变量范围上界,Hbk为第k个设计变量范围下界,迁移参数fc,最大迭代次数为Lmax,变异概率为Pmut,0 2)由火箭回收舱段定位系统主站测量g时刻舱段辐射信号到达各基站的时间差测量向量(g)。 3)设置当前迭代次数l=1,对量子海鸥种群进行位置初始化,海鸥个体当前位置由量子位的概率幅编码和Bernoulli 混沌映射确定。 4)进行量子海鸥个体搜索,根据到达时间差测量向量Δt→(g)按照式(6)计算每只量子海鸥的量子适应度值,随后按适应度值排序搜索截止当前代的最小值YBest(l)和最佳位置XBest(l)。 5)进行量子海鸥位置更新。依次执行迁徙、攻击和变异反向学习行为,使每只海鸥移动到新的位置,令l=l+1。 6)判断t是否达到最大迭代次数Lmax,如达到则停止迭代,并输出最优解YBest(l)和最佳位置XBest(l),令XBest(l)为g时刻火箭回收舱段位置坐标;否则回到第4 步,循环迭代进行搜索。 7)判断定位是否结束,如果结束则退出;否则返回第2 步,等待获取下一时刻到达时间差测量值的。 本节通过仿真试验对所提出QSOA 的有效性进行验证,然后测试基于QSOA 的运载火箭回收舱段TDOA 定位方法的定位性能。 为验证所提出QQSOA 的可行性,将本文改进的QSOA 与遗传算法、QSOA 和被囊群算法进行对比,选择经典的30 维单峰测试函数F1、F2,30 维多峰测试函数F3、F4,固定维度多峰函数F5、F6,具体函数表达式见表1,其中函数F5 的参数ai、bi见表2。 表1 测试函数表Tab.1 Test functions 表2 Kowalik 函数参数表Tab.2 Parameters of the Kowalik function 为了降低偶然性对性能测试结果的影响,对每个测试函数均进行30 次独立实验后,从最优值、平均值和标准差3 个方面进行算法性能对比,实验设置种群规模为30,最大迭代次数为250,每个函数的平均收敛结果如图4 所示。表3 给出了4 种算法对各测试函数的寻优统计结果。 表3 测试函数优化计算统计结果Tab.3 Statistical results of the test functions 图4 测试函数平均收敛曲线Fig.4 Average convergence curves of the test function 由图4 可知,对于单峰函数、多峰函数、固定维度多峰函数而言,量子海鸥算法的收敛速度比其余算法能力大幅提高。由表3 可知,从最优值、平均值和方差来看,QSOA 相比其余算法局部搜索能力更强,寻优精度明显更高。可见QSOA 在全局寻优能力和局部搜索能力方面的平衡性更好,即提高了收敛速度,又具有更高的寻优精度,结果稳定性更好。 以函数F6 为例,通过SOA 和QSOA 寻优过程中种群分布变化,验证QSOA 对种群多样性的提升效果,分别对比迭代次数为100、200 和迭代结束后的种群分布,两种算法寻优迭代过程中种群分布情况如图5 所示。由图5 可知,基本SOA 在寻优过程中种群逐渐收敛到局部极值,缺乏对空间的充分覆盖能力,容易陷入局部极值,全局搜索精度差。而所设计的QSOA 引入变异反向学习机制后,不仅能够覆盖理想最优解附近,而且在迭代过程中始终维持一部分种群个体在最优解附近区域以外较远区域,提升了种群多样性,降低陷入局部极值的概率。 图5 种群散布随迭代次数变化Fig.5 Population dispersion with the iteration number 针对重复使用运载火箭一级回收舱段运动轨迹进行定位,火箭一子级分离后一般先后经过掉头调姿、飞回点火、再入点火、气动控制和着陆点火5个阶段,在高精度控制下最终以预定的速度、位置和姿态垂直回收。火箭一级舱段在分离后的飞行运动轨迹如图6 所示[5]。 图6 可重复使用火箭回收舱段在分离后的飞行轨迹Fig.6 Flight trajectory of the reusable rocket recovery module after separation 图6 中,0 为起飞时刻;1 为一级关机时刻,该时刻火箭高度、速度和弹道倾角分别为(62.6 km,1 682 m/s,42°);2 为飞回点火时刻,该时刻各参数为(83.4 km,1 538 m/s,38°);3 为飞回关机时刻,各参数为(114 km,587 m/s,34°);4 为飞行最高点,各参数为(120 km,480 m/s,0°);5 为再入点火点,各参数为(48 km,1 256 m/s,-65°);6 为着陆点火时刻,各参数为(4.4 km,312 m/s,-71°)[5]。 定位系统4 个地面 基站在水平面呈正方形分布,半对角线距离为R,如图7 所示。各基站位置与回收舱段位置关系如图8 所示,红色五角星表示主站位置。设置测量到达时间差的误差服从均值为0 s,方差为20 ns 的正态分布误差。 图7 定位基站构型Fig.7 Positioning base station configuration 图8 定位基站与回收舱段位置关系Fig.8 Positioning relationship between the base station and the recovery cabin 为了验证使用QSOA 进行火箭回收舱段TDOA 定位的性能,分别采用Chan 算法、标准SOA算法和本文提出的QSOA 算法对如图2 所示的火箭回收舱段飞行轨迹进行定位解算,对比3 种方法的定位性能。选择阵型间距为R=10 km、25 km、50 km,定位误差对比如图9~图11 所示。 图9 基站构型间距R =10 km 时3 种算法的定位结果Fig.9 Positioning results obtained by three algorithms when the square base station configuration spacing R =10 km 图10 基站构型间距R =25 km 时算法定位误差对比Fig.10 Comparison of algorithm positioning errors when the square base station configuration spacing R =25 km 图11 基站构型间距R =50 km 时算法定位误差对比Fig.11 Comparison of algorithm positioning errors when the square base station configuration 表4~表6 从定位误差均值、定位误差方差和最大定位误差3 个方面对3 种算法的定位性能进行了对比。在定位误差均值方面,标准海鸥算法相比Chan 算法平均提升幅度为16.5%,最大提升幅度为25.5%。QSOA 相比标准海鸥算法平均提升幅度为21.5%,最大提升幅度为34.4%。在定位误差方差方面,标准海鸥算法相比Chan 算法平均提升幅度为31.1%,最大提升幅度为35.4%。QSOA 相比标准海鸥算法平均提升幅度为21.2%,最大提升幅度为25.58%。在最大定位误差方差方面,标准海鸥算法相比Chan 算法平均提升幅度为24.1%,最大提升幅度为30.7%。QSOA 相比标准海鸥算法平均提升幅度为20.1%,最大提升幅度为28.45%。对比图9~图11 中标准海鸥算法和QSOA 的定位误差图,可以看出引入量子编码、混沌初始化后在定位初期QSOA 收敛更快,波动更小。由定位误差性能分析可知引入量子编码和遗传方向学习后QSOA 相比标准海鸥算法的全局寻优能力更强,对最优值的求解精度更高。此外,从不同间距下的定位误差变化情况上可以看出,基站构型间距越大定位精度越高,在条件允许的情况下基站间距可以尽可能大一些。 表4 3 种算法定位误差均值对比Tab.4 Comparison of the average positioning errors obtained by three algorithms 表5 3 种算法定位误差方差对比Tab.5 Comparison of the positioning error variances obtained by three algorithms 表6 3 种算法最大定位误差对比Tab.6 Comparison of the maximum positioning errors obtained by three algorithms 本文将量子理论、混沌映射和遗传反向学习机制与SOA 相结合提出了一种QSOA,将QSOA 应用于运载火箭回收舱段TDOA 定位求解问题中,通过量子理论和混沌映射提高了初期种群对优化空间的全局覆盖能力,改进了早期收敛能力。引入量子旋转门和遗传方向学习机制,改善了算法全局搜索与局部最优求解难以兼顾的缺陷。通过开展运载火箭回收舱段定位仿真试验,验证了QSOA 在火箭舱段无源定位解算方面的应用可行性,对算法定位性能提升度进行了量化分析。5 仿真试验及分析
5.1 QSOA 有效性验证



5.2 定位目标及仿真设置


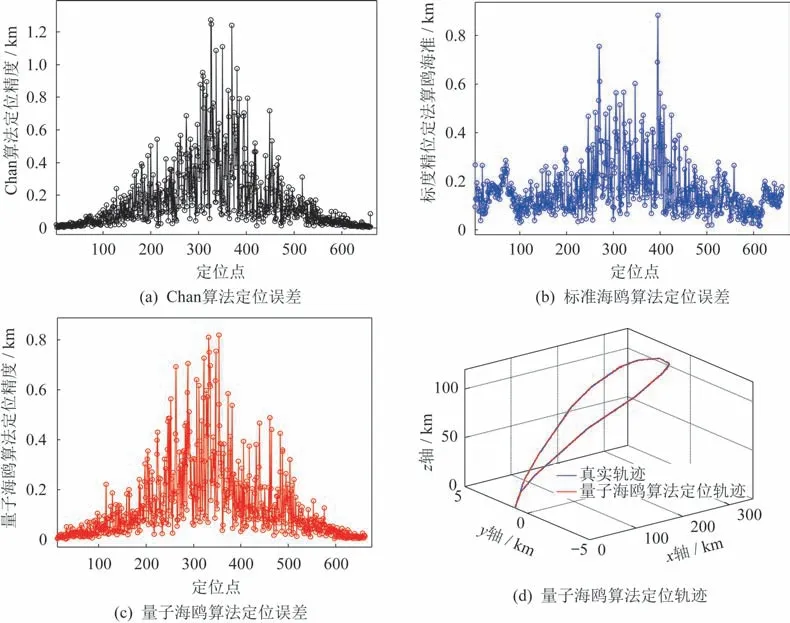
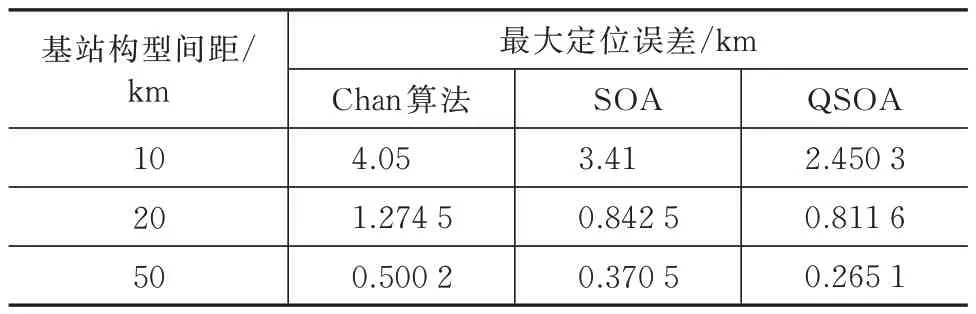
5.3 定位精度分析




6 结束语
