驱动模式和转速对某星载天线扰动特性的影响

杨 可，陈 薄，贾清健，古忠涛

（1.西南科技大学 制造科学与工程学院 制造过程测试技术教育部重点实验室，四川 绵阳 621010；2.西安空间无线电技术研究所，陕西 西安 710100）

0 引言

空间天线（包括星载天线）是典型的高柔性、低阻尼结构，在其姿态调整过程中，驱动单元（电机和减速器系统）输出产生的扰动经天线结构传递并最终作用于航天器本体［1-3］。如这一扰动过大或与航天器的运动耦合，将对航天器的指向精度和运行稳定性造成严重影响，进而影响航天器的在轨工作性能［4-5］。因此，分析空间天线结构的扰动特性，可为天线的微振动设计提供理论参考依据，进而提升航天器系统的微振动控制水平，具有显著的学术和工程意义。

空间天线扰动的频率范围宽、振动幅值小、影响因素较多，且与天线的结构有较大关系［6-10］，受限于理论分析技术和试验条件。截至目前，研究人员对空间天线的扰动特性和所涉及关键技术的理解仍较为有限。MEGURO 等［11-14］开展某大型天线开展过程的动力学响应地面测试试验，测量天线展开和关闭过程中若干环节的扰动加速度、扰动力和力矩，与天线在轨动力学响应对比，指出合理的地面测试试验可定性预测天线的在轨动力学响应。SHEN 等［15］采用Abaqus 和Admas 软件协同仿真的方法展开分析，得出通过薄膜天线中薄膜型面的固有频率和振型，发现薄膜型面的固有频率与其预应力的平方根成正比。KORNIENKO［16］建立天线驱动单元的数学模型，借助驱动单元输出转矩试验，利用系统参数辨识方法，获取数学模型中的关键参数，对比输出转矩计算结果与试验结果的时域和频域，验证模型的正确性。伍时建等［17-18］建立某中继天线驱动单元（步进电机和谐波减速器）的数学模型，利用Matlab/Simulink 仿真分析驱动单元输出角加速度的扰动幅频特性，与天线简化结构的扰动力幅频特性试验结果对比，揭示驱动单元与天线系统扰动的定性映射关系。朱仕尧［19］采用Nastran 和Adams 软件建立某数传天线的动力学分析模型，分析天线单轴驱动和双轴驱动模式下安装界面的扰动力和力矩变化规律，结果表明，相较于单轴驱动，双轴驱动时天线扰动呈现一定程度的叠加。王朋朋等［20］研究某大型可展天线的扰动特性，分析影响扰动基频的关键因素，通过结构优化设计，降低星体扰动对天线结构的敏感度。戴宇航等［21］针对一种可折展式空间天线，采用有限元分析的方法，研究折展机构中杆件尺寸对天线固有频率的影响，结果表明，折展机构中上下支杆和斜撑杆尺寸对天线结构固有频率影响较大。王辉等［22］采用仿真分析与试验相结合的方法，研究某型中继天线中驱动电机、驱动单元（电机和减速器等）及天线结构的扰动特性，探讨驱动单元输出频率与天线固有频率对天线结构扰动频率的影响。

较为准确的天线扰动特性分析有赖于精确的动力学模型和微重力环境下的地面台架试验。本文针对某型星载双轴指向天线，采用Ansys 和Adams 软件联合仿真的方法，建立其多柔体系统动力学分析模型，通过天线微重力环境下的地面微振动测试，验证动力学分析模型的可靠性。基于多柔体系统动力学分析模型，分析不同驱动模式与转速条件下的天线扰动特性，为此型天线的微振动设计与抑振策略制定提供技术支持。

1 天线的动力学分析模型

1.1 天线结构

本文分析的星载双轴指向天线主要由展开支座、展开臂、X/Y双轴转动机构和反射器组件、馈源组件及附属部件组成，如图1 所示。其中，展开支座是天线与卫星本体的分界面，同时也是天线的安装固定件，控制天线的展开与锁定；展开臂是天线的支承部件，其两端分别连接展开支座与X/Y双轴转动机构；X/Y双轴转动机构包含X轴转动单元、Y轴转动单元及对应的转动支架，转动单元驱动转动支架运动，实现反射器组件绕X和Y这2 个转动轴双自由度转动。天线姿态调整过程中，转动单元（电机和谐波减速器）产生扰动（微振动），经转动机构、展开臂和展开支座，最终传递至卫星本体。

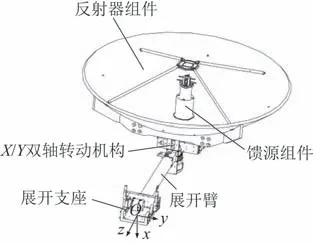
图1 星载双轴指向天线结构Fig.1 Structure of the dual-axis spaceborne antenna

1.2 天线结构的有限元模型

天线结构几何建模时省略构件中对扰动特性影响较小的馈源组件和局部微小结构（如零件中的工艺圆角等），对轴承、标准连接件（螺栓、螺钉等）等，根据作用等效原则进行结构简化处理。基于此，经简化处理后的天线几何模型如图2 所示。

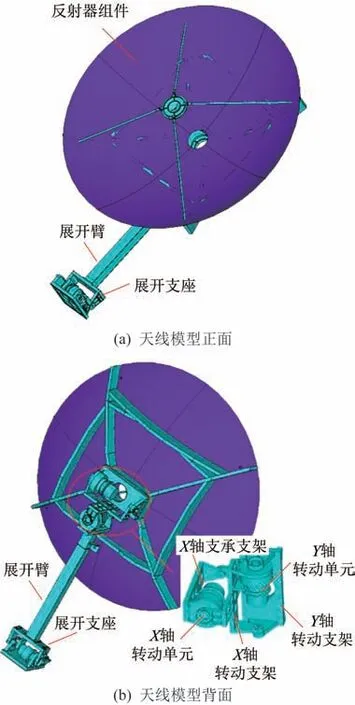
图2 简化后的天线模型Fig.2 Simplified antenna model

采用Ansys 软件建立天线结构有限元模型，考虑到多柔体动力学模型中构件间的运动学和动力学关系，将天线结构分为支承部件、转动部件和反射部件3 部分并独立建模。其中，支承部件包括展开支座、展开臂、X轴转动单元和X轴支承支4 大组件；转动部件包括Y轴转动单元与X轴转动支架；反射部件包括反射器组件和Y轴转动支架。天线反射器型面的厚度远小于其他2 个方向尺寸，属于典型的壳体结构，因此有限元模型中将其简化为壳单元，其余结构按实体建模。展开臂为类似方管结构，结构较为简单，采用六面体网格，反射型面采用四边形网格，其余部分采用四面体网格，天线结构的各部件的网格模型如图3 所示。

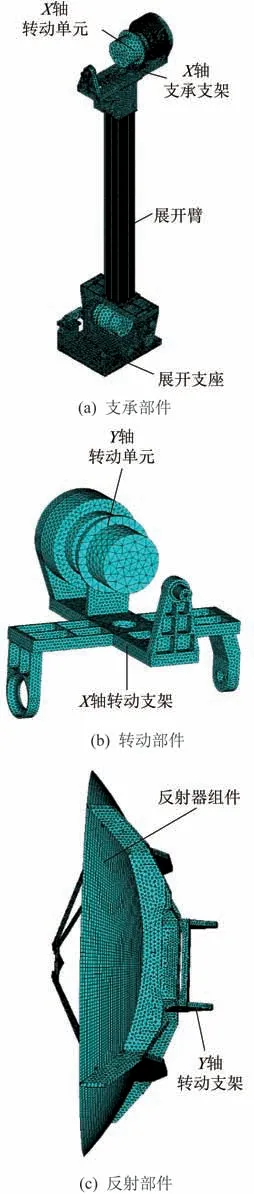
图3 天线结构的3 大部件Fig.3 Three parts of the antenna

天线结构中大多数构件采用的材料均为铝合金，反射器型面采用的材料为蜂窝夹层板，是一种复合材料，其蒙皮为碳纤维M40J（密度为1.77×103kg·m-3），厚度为0.1 mm；蜂窝芯材为铝合金，厚度为15.0 mm。在有限元模型中，准确地描述其材料特性较为困难，根据文献［23-26］，将蜂窝夹层板等效为各向同性的均质薄板，其等效弹性模量Eeq为

式中：E为蜂窝芯材的弹性模量，Pa；hf为蒙皮板的厚度，mm；hc为铝蜂芯材的厚度，mm。

等效密度ρeq为

式中：ρf为碳纤维M40J 蒙皮的密度，kg·m-3；ρs、t分别为蜂窝芯材的密度和壁厚，mm。

由式（1）、式（2）可得蜂窝夹层板等效后的弹性模量和密度，有限元模型中所涉及的材料及其主要物理特征参数见表1。

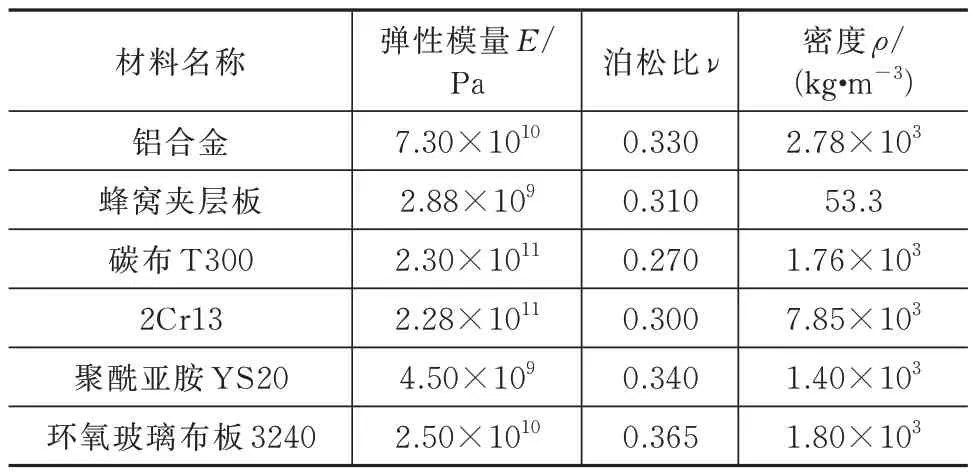
表1 天线零部件的材料及主要物理特性参数Tab.1 Material and physical characteristic parameters of the antenna parts

1.3 天线结构的多柔体系统动力学分析模型

采用MSC.Adams 软件，构建天线结构的多柔体系统动力学分析模型，分析动力学瞬态响应。首先在Ansys 软件中，分别将支承部件、转动部件和反射部件的有限元模型转换为模态中性文件，然后通过Adams 软件中的Adams/Flex 接口，将模态中性文件依次导入工作空间，经组装形成动力学分析的天线结构模型。其约束条件定义如下：

1）定义反射部件与转动部件之间、转动部件与支承部件之间为转动约束。

2）实际情况下，展开支座底面（测试面）是与航天器固定连接的，因此展开支座底面设置为全约束，即约束底面所有自由度。

转动单元输出转矩的波动产生天线结构的扰动激励，结构动力学瞬态响应分析时，转动单元实验得到输出转矩为驱动力矩。X轴单轴驱动时，在X轴转动单元输出轴端对应的转动约束位置施加驱动转矩，Y轴转动单元输出轴端对应的转动约束位置则设置为全约束；Y轴单轴驱动时，处理方式与X轴相反；双轴同时驱动时，上述2 个转动约束位置同时施加驱动转矩。由于天线在轨运行时处于微重力环境，因此分析中不考虑重力影响。通过上述技术处理，得到天线结构的多柔体系统动力学分析模型，如图4 所示。

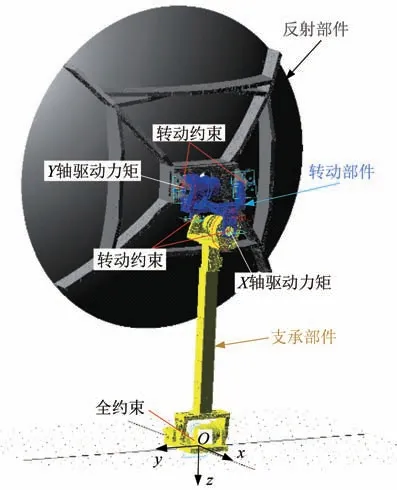
图4 天线多柔体系统分析模型Fig.4 Analysis model of the multi-flexible-body system for the antenna

2 天线结构的微振动试验

天线微振动测试试验装置如图5 所示，主要由气浮装置、天线本体（拆除反射器组件）、转接工装、配重块、高精度平台、6 自由度力传感器（型号：KISTLER9119AA2）和计算机等组成。将6 自由度力传感器设置于天线展开支座底部，通过转接工装分别与天线支座和固定装置固接；固定装置是试验装置中的承载结构，固定转接工装，同时悬臂支承天线本体；气浮装置安装于高精度平台上，安装位置为天线本体正下方。

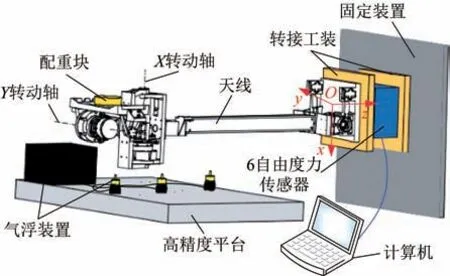
图5 天线微振动测试试验装置Fig.5 Test devices for measuring the micro-vibration of the antenna

试验在地面重力环境下进行，天线的驱动模式为X轴单轴驱动，驱动转速为0.4 °/s。由于反射器组件体积较大，安装调试过程较为复杂，试验过程中拆除天线结构的反射器组件，将其影响等效为具有相同转动惯量的配重块，施加于转动机构。为模拟太空微重力环境，采用气浮升力平衡重力的作用，根据试验装置的重量调整气浮升力的大小。采用6 自由度力传感器，测量X轴转动单元（电机+谐波减速器组件）驱动天线转动过程中引起的天线结构微振动，测量结果经采集后传输至计算机中存储。测量结果经滤波降噪、傅里叶变换后，得到扰动力和扰动力矩试验结果。

3 结果分析与讨论

航天器的扰动（微振动）特性通常用结构的扰动力和扰动力矩评价，本文采用天线展开支座底部的扰动力和扰动力矩描述天线结构的扰动特性展开分析。Fx、Fy和Fz分别表示支座底部X、Y和Z3 个坐标方向的扰动力，Mx、My和Mz分别表示对应坐标方向的扰动力矩。

3.1 试验结果与动力学分析结果的对比

X轴单轴驱动模式下，驱动转速为0.4 °/s 时，扰动力及扰动力矩的试验结果与动力学分析结果的幅频曲线如图6 和图7 所示。

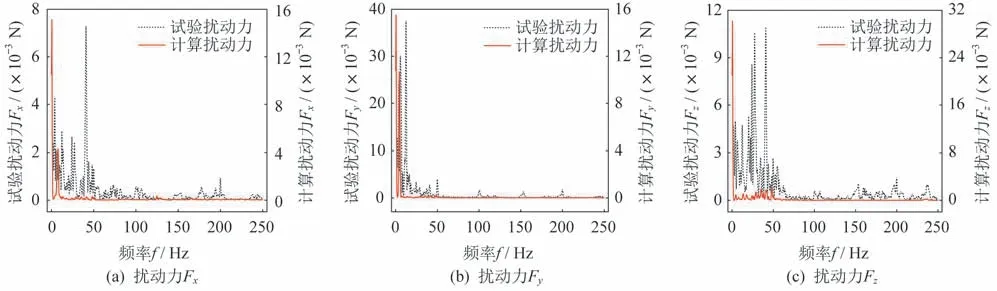
图6 扰动力动力学分析结果与试验结果的频谱特性对比Fig.6 Comparison of the spectral characteristics of the disturbance force obtained by calculations and tests

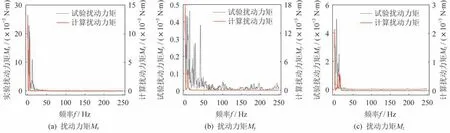
图7 扰动力矩动力学分析结果与试验结果的频谱特性对比Fig.7 Comparison of the spectral characteristics of the disturbance torque obtained by calculations and tests

由图6 和图7 可知，扰动力和扰动力矩的动力学分析结果与试验结果的谱峰值差异性较大，但主要谱峰值对应的频率均主要集中在频率f=0～50 Hz低频段，较为符合空间天线这类大柔性结构的微振动频率特性，在一定程度上证明了本文所述动力学分析模型的可靠性。动力学分析结果与试验结果的较大差异，是多因素综合影响的结果：①天线结构扰动能量微小且较为敏感，不但需要精密的测量仪器，同时测量较为困难且易于受环境干扰，测量结果含有大量噪声信号；② 测量结果的数据处理难度较大，滤波降噪难以完全消除噪声信号，试验结果中不可避免地存在噪声信号，因此试验结果存在不确定性；③动力学分析中对天线结构的简化处理，使得动力学分析模型与实际结构存在固有差异，一定程度上影响计算结果的准确性。因此，动力学分析结果与试验结果存在一定的差异性。

在典型频率下，天线结构扰动力和扰动力矩试验结果与动力学分析结果的对比见表2 和表3。表中的标准频率为天线结构的主要结构频率，是微振动分析中的关注的重要频率点。由表2 和表3 可知，在绝大多数典型频率点，扰动力和扰动力矩的动力学分析结果均小于试验结果，仅在频率f=7.430±0.5 Hz 时，出现动力学分析结果大于试验结果的情况。频率f=7.324 Hz 时，扰动力Fx和扰动力矩Mx的动力学分析结果大于试验结果，但前者的动力学分析结果与试验结果相差不大，均在同一数量级，而后者的动力学分析结果与试验结果之间相差较大，动力学分析结果比试验结果大一个数量级。综上所述，动力学计算结果可反映天线结构的微振动特性。

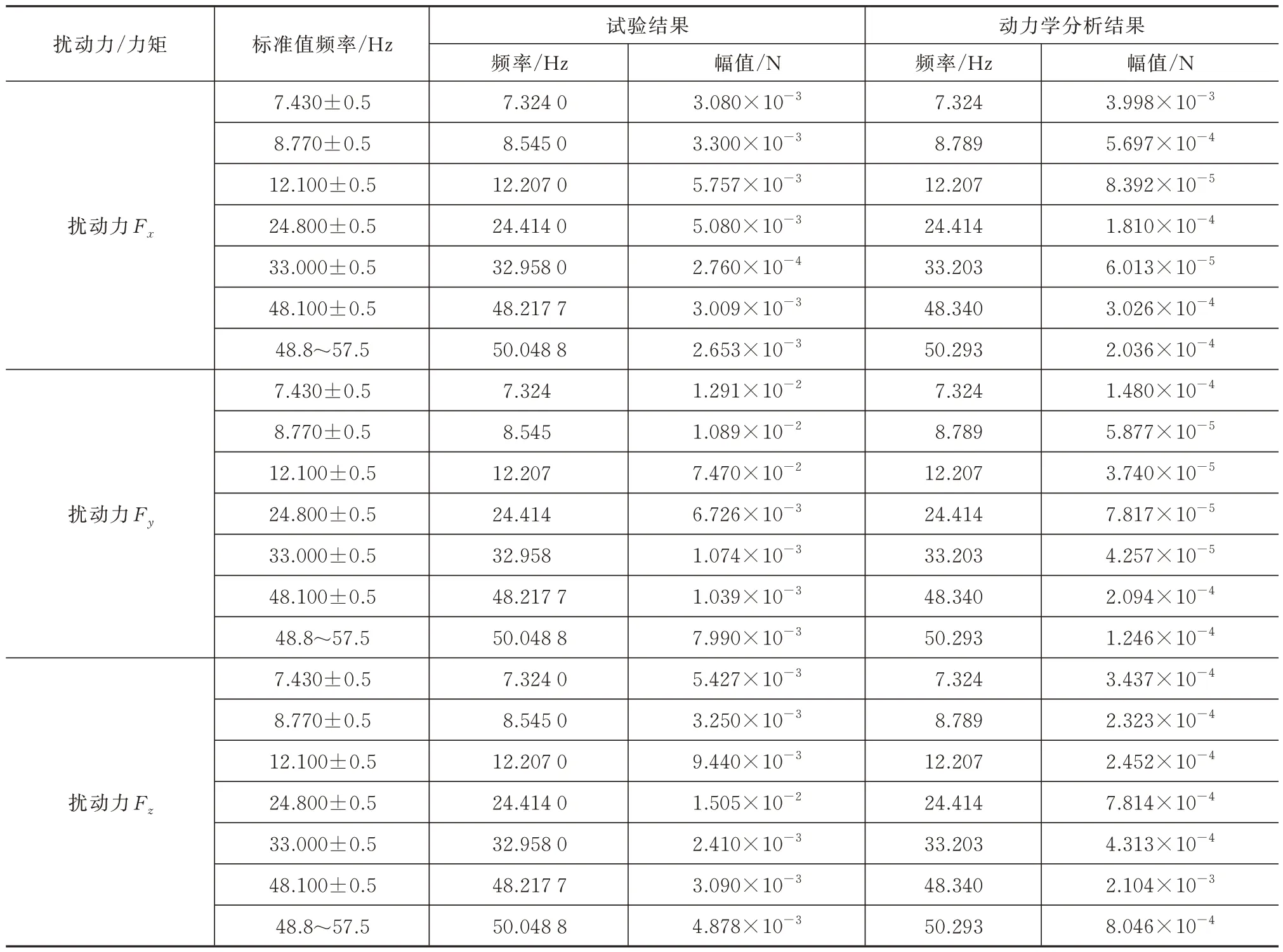
表2 典型频率下天线结构扰动力动力学分析结果与试验结果的对比Tab.2 Comparison between the dynamic analysis results and test data of the antenna disturbance force at typical frequencies

表3 典型频率下天线结构扰动力矩动力学分析结果与试验结果的对比Tab.3 Comparison between the dynamic analysis results and test data of the antenna disturbance torque at typical frequencies

3.2 驱动转速对天线扰动特性的影响

X轴和Y轴单轴驱动模式下，以及XY双轴同时驱动模式下，驱动转速对天线扰动的影响相似，因此分析驱动转速对天线扰动特性的影响时，仅给出X轴单轴驱动模式的动力学分析结果。

动力学分析获得的X轴单轴驱动模式下，驱动转速对扰动力和扰动力矩的影响如图8 和图9所示。

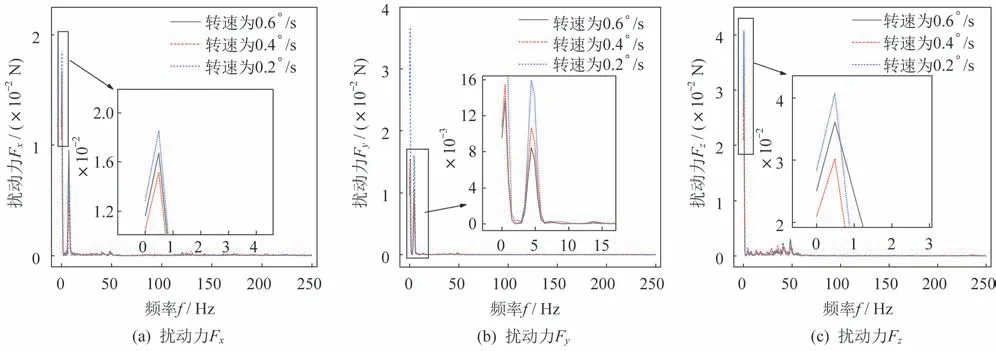
图8 驱动转速对扰动力的影响Fig.8 Effects of the driving rotational speed on the disturbance force

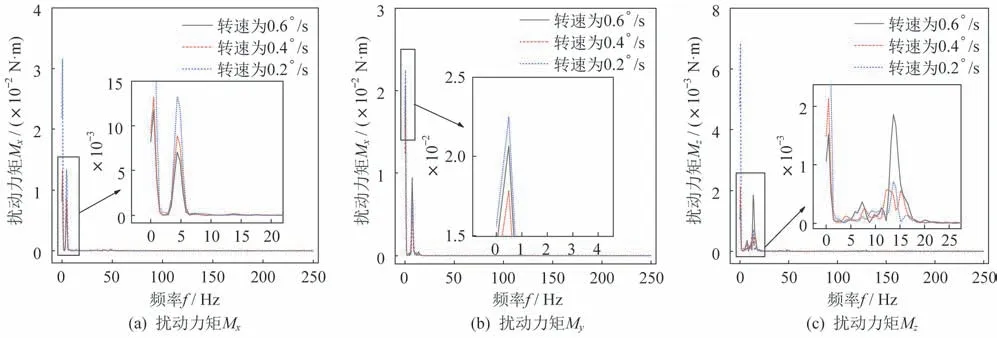
图9 驱动转速对扰动力矩的影响Fig.9 Effects of the driving rotational speed on the disturbance torque

由图8 可知，3 种驱动转速下，X、Y和Z3 个方向扰动力的主要频率分布较为相似，即驱动转速并未对天线的扰动频率产生影响。驱动转速主要影响的是扰动力幅值，即扰动强度，当驱动转速n=0.2 °/s 时，天线结构低频段内，较多频率点的扰动力幅值是3 种转速中最大的，表明在此驱动转速下，转动单元的微振动与天线结构产生了一定程度的耦合，使得天线结构的扰动加强。

由图9 可知，驱动转速对扰动力矩的影响较为复杂。3 种驱动转速下，在主要频率点，扰动力矩Mx驱动转速增大，呈逐渐增大的趋势。扰动力矩My受驱动转速的影响无明显的规律性，但可以看出，驱动转速n=0.2 °/s 时，天线的扰动力矩Mx和My最大，即该驱动转速增大了天线的扰动力矩。另外，相对于Mx和My，扰动力矩Mz是较小的（小一个数量级），从扰动力矩来看，X方向和Y方向扰动更为激烈。

综上所述，单轴驱动模式下，X轴和Y轴方向的扰动更为剧烈，天线结构的扰动特性由这2 个方向的扰动力和扰动力矩主导。

3.3 驱动模式对天线扰动特性的影响

为研究驱动模式对天线结构扰动特性的影响，计算驱动 转速n=0.4 °/s 条件 下，X轴单 轴驱动、Y轴单轴驱动及XY双轴同时驱动3 种驱动模式的天线动力学响应。

3 种驱动模式下扰动力和力矩的动力学分析结果如图10 和图11 所示。

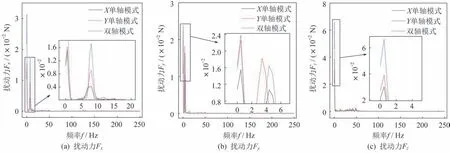
图10 驱动模式对扰动力的影响Fig.10 Effects of the driving mode on the disturbance force

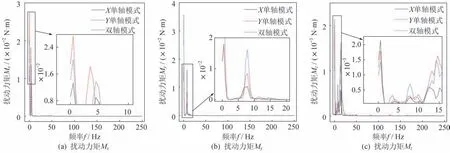
图11 驱动模式对扰动力矩的影响Fig.11 Effects of the driving mode on the disturbance torque

由图10 可知，3 种驱动模式下，X、Y和Z3 个方向的扰动力主要频率分布较为接近，表明驱动模式对结构的主要频率未产生明显影响。Y轴单轴驱动时的扰动力明显大于X轴单轴驱动，表明单轴驱动时，Y轴单轴驱动的扰动更为剧烈。相对于单轴驱动，XY双轴同时驱动时，X和Z方向的扰动力Fx和Fz在f=0～50 Hz 的低频段更大，而Y方向的扰动力Fy的变化则较为复杂，某些频率点双轴同时驱动的扰动力反而小于Y轴单轴驱动，即扰动力得到一定程度的抑制。综合分析X、Y和Z3 个方向的扰动力可知，相对于单轴驱动，XY双轴同时驱动时，天线的扰动得到一定程度的叠加。

由图11 可知，3 种驱动模式下，Z方向的扰动力矩Mz最小，与X和Y方向的扰动力矩Mx和My相差1 个数量级，天线的扰动力矩主要受Mx和My影响。扰动力矩Mx和My与驱动模式的关系不同，扰动力矩Mx在Y轴单轴驱动时更大，而扰动力矩My在XY双轴同时驱动时更大。

综上所述，与单轴驱动相比较，双轴驱动模式下天线结构的扰动更为剧烈，扰动力和扰动力矩的变化也更为复杂，表明X轴和Y轴转动单元同时驱动时，可能引起一定程度上的扰动叠加。

4 结束语

本文针对某型星载双轴指向天线在典型工况下的扰动特性展开研究。基于Ansys 软件和Admas软件，建立天线结构的多柔体系统动力学分析模型，计算典型驱动条件下天线结构的扰动力和扰动力矩，并通过天线地面微振动物理试验，验证动力学分析方法的可靠性，主要得出以下结论：

1）基于Ansys 和Admas 软件，建立天线多柔体系统动力学分析模型，明确预测天线结构的扰动特性，空间天线属于高柔性、低阻尼结构，扰动主要集中在频率f=0～50 Hz 低频段。

2）天线结构的扰动频率与驱动转速和驱动模式无明显的关系，驱动转速和驱动模式主要影响扰动的强度，即扰动力和扰动力矩的幅值；单轴驱动模式下，驱动转速n=0.2 °/s 时，典型频率点，天线的扰动力和扰动力矩最大，结构的扰动更为剧烈；相较于单轴驱动，XY双轴同时驱动时，大多数典型频率点的扰动力和扰动力矩更大，表明X轴和Y轴转动单元同时驱动可能引起一定程度上的扰动叠加。

3）扰动力和扰动力矩试验结果与动力学分析结果的较大误差，有望通过发展并完善测试方法和技术，同时建立精确的天线动力学分析模型得到一定程度的改善。在微振动试验中，通过严格控制试验装置的装配精度减小系统误差，采用更为先进的滤波降噪技术减少测试结果中的环境噪声信号，有助于提升试验结果的可靠性；动力学分析中，建立更加符合实际的天线结构精确动力学分析模型，提升动力学分析结果的准确性。上述措施是提升试验结果与动力学分析结果吻合性较好的技术途径。