一种空间对接机构的简化建模方法及其在实验舱侧向再对接中的应用
2024-01-08胡雪平沈晓鹏刘璟龙甘克力柏合民
胡雪平,沈晓鹏,刘璟龙,甘克力,柏合民,罗 斌
(1.上海宇航系统工程研究所,上海 201109;2.上海航天技术研究院,上海 201109)
0 引言
异体同构周边内翻式对接机构是中国载人航天交会对接的关键且极其复杂的机构,用于实现空间两飞行器的连接与分离。张崇峰、肖余之、时军委等[1-18]进行了长久深入的研究,文献中给出了对接机构设计组成和原理,以及针对不同对接目标的对接机构的缓冲参数设计,详述了对接机构的动力学仿真,提到对接动力学研究具有长期性和复杂性。但是,对接机构与转位机构耦合的动力学分析尚未得到深入研究。随着载人空间站工程的发展[19-25],对接机构需要与其他机构一起协同完成空间站的组建,如转位机构和机械臂等,在空间站组建过程中,有时这些机构同时工作,如将转到核心舱侧向后的侧向再对接,是对接机构与转位机构两大复杂机构典型耦合的动力学过程,侧向再对接动力学模型求解极其困难,但又是空间站组建过程中典型的动力学过程,必须经过仿真和试验验证。在对接机构研制过程中,对接机构动力学仿真模型经过了由简单到详细、由详细再到简单2 个阶段。第1个简单指早期研究阶段,详细的设计方案和很多参数还不具备,没办法进行详细建模;第2 个简单阶段,虽然已有详细的仿真模型,但针对不同的动力学过程,基于运动过程准静态的运动特点,侧向再对接过程建模就是如此。再对接通过主驱动机构电机缓慢匀速推出对接环,直到捕获被动对接机构,不同于两航天器通过有相对速度的碰撞对接会产生较大的惯性力,捕获时间较短,在轨接近中速正碰工况约1 s 完成捕获,再对接则需要上百秒才能完成,如果对接机构和转位机构模型都进行详细建模,不仅模型复杂,计算时间长,还容易出错,效率很低,因此,在对接机构有详细模型以及工程实践的基础上,可以对机构经过不损失性能特点的适当化简,建立简化模型,并确定合理可行,用于和转位机构一起建立耦合动力学模型,其精度能够满足工程需求。
1 对接机构模型
实验舱侧向再对接如图1 所示,转位机构已将实验舱从轴向对接口转位到侧向对接口,侧向再对接捕获过程中,对接机构与转位机构双关节耦合工作。

图1 侧向再对接Fig.1 Schematic diagram of lateral redocking
实验舱对接机构的捕获缓冲系统是实现再对接的主要功能机构,对接机构简化建模是针对捕获缓冲系统进行简化的。
对接机构的捕获缓冲系统主要包括对接环、捕获锁、丝杠联系组合、丝杠安装组合、差动组合和主驱动组合6 个功能单元。其中:对接环由3 个导向板和1 个对接环组成,主要起导向消除主被动环初始偏差的作用;捕获锁在两对接环贴合过程中实现两对接环的柔性连接;丝杠联系机构由一对滚珠丝杠副和丝杠联系机构组成,单轴弹簧机构、电磁阻尼器各自分别通过锥齿轮与丝杠联系,丝杠联系组合的功能是分管对接环横向、滚转方向的运动自由度和缓冲性能;丝杠安装组合提供6 根丝杠的安装、摆动及向差动组合的运动传递;差动组合由3 个相互嵌套的差动器和部分中间传动轴组成,双轴弹簧机构装于其中2 个差动器中,差动组合对丝杠联系组合的输出进行差动,提供对接环偏航、俯仰方向的自由度和缓冲性能;丝杠联系组合与差动组合间由中间弹簧机构联系;主驱动组合前装有自动调整摩擦制动器和始端弹簧机构,它们与中间弹簧机构提供对接机构轴向的缓冲性能。
由此,对接机构的6 个功能单元相互配合最终实现了捕获,并缓冲衰减对接环6 自由度运动的效果,即当对接环受到外在冲击时(如空间飞行器存在相对运动速度所致),对接机构的缓冲系统对于对接环等效于一个空间六维力作用于主动对接环,使主动对接环和实验舱具有一定的刚度、阻尼特性,能够缓冲和衰减对接环受到的外在冲击能量。基于此,进行对接机构简化建模,并与对接机构整机试验性能曲线进行对比,确保对接机构的性能合理正确。
1.1 对接机构动力学模型
主动对接机构的力传递路径主要分3 个层次:对接环、丝杠、弹簧阻尼等元件。对接环(含导向板)接触作用力传递至与对接环胡克铰接的6 根丝杠,如图2 所示,将引起6 根丝杠长度变化;丝杠的作用力,一端通过与对接环的胡克铰接传递丝杠联系组合中的齿轮传动,最终转化成扭转单轴弹簧和阻尼器的力矩,卷紧弹簧,存储能量,另一部分能量被阻尼器消耗;另一端通过与丝杠螺旋连接的螺母传递至中间弹簧及差动组合(含双轴弹簧、始端弹簧和摩擦制动器)。
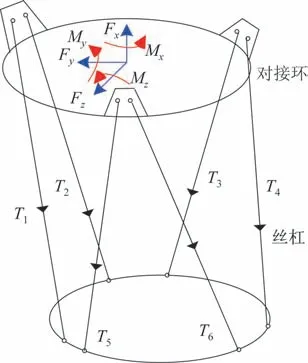
图2 对接机构受力分析Fig.2 Force analysis of the docking mechanism
对接机构的动力学模型从对接环的动力学分析入手,对接环受到外力Fw(可分解空间3 方向力Fx、Fy、Fz和力矩Mx、My、Mz),以及6 根丝杠的作用力Ti。
式中:q=(x,y,z,φ,ψ,θ)为对接环的3 方向位移和姿态角位移,为3方向速度和姿态角速度,M(q,)为位移和速度的函数,并包含对接环质量、惯量等参数。FT1(Ti)为6 根丝杠作用力的函数。
对接机构中弹簧阻尼元件的存在表明:当对接环使每一个丝杠移动时,在每根丝杠上将作用有一个阻挠力Ti,i=1,2,…,6,作用于i丝杠的阻挠力,以力矩Mri的形式传递到齿轮,考虑到齿轮的惯性,对其进行受力分析:
式中:Mri=Mri(θsspj,),j=1,2,3;Mai=Jμi,i=1,2,…,6,Jμi为齿轮的转动惯量,为齿轮的角加速度。
差动组合如图3 所示,由3 个差动器组成,其中布局了2 个双轴弹簧,外接一个始端弹簧和摩擦制动器[13-20]。

图3 差动组合Fig.3 Differential combination
差动组合的动力学分析要针对每个主要的齿轮(输入齿轮、与双轴弹簧连接的齿轮等)进行受力分析,通过中间弹簧机构力Mmidj和双轴弹簧机构和始端弹簧机构(含摩擦制动器)力Mdspj和丝杠作用力Ti的关系式:
求解动力学方程,要进行运动学分析,与动力学力传递路径的3 个层次对应,运动学分3 个层次:双轴弹簧、始端弹簧(含摩擦制动器)的运动通过差动组合、中间弹簧机构传递至与丝杠螺旋连接螺母;单轴弹簧机构和阻尼器的运动传递至与丝杠联系组合胡克铰接的丝杠;6 根丝杠螺母的协调运动决定了对接环刚体6 自由度的运动。
综上所述,主动式对接机构建模具有一定的复杂性。如果从另外一个角度考虑,不去关注对接机构的对接环、丝杠螺母、齿轮、弹簧阻尼器等传动缓冲的精确力传递关系,而是关注其整体性能,建立如空间六维弹簧阻尼模型来代替实际对接机构的整体作用效果,即假设对接环与安装对接机构的实验舱之间作用着一个非线性的六维广义力,如图4所示。

图4 对接机构缓冲系统Fig.4 Buffer system of the docking mechanism
在这个阶段,简化模型有着对接机构详细模型和工程实践的双重基础,对接机构详细模型可以进行整机仿真,输入各向运动指令,绘制相应方向的位移或角位移与力或力矩的关系,对接机构整机试验台也积累了整机试验的结果,可以提取出各向整机性能的测试结果。对详细的对接机构模型,纵向即x方向施加1 mm/s的速度进行压缩到70 mm,其他y和z方向施加1 mm/s 的速度进行拉偏到±100 mm并同速恢复到零位,绕x、y、z3 方向施加0.1°/s 的角速度进行转动方向的拉偏到±10°并同速恢复到零位,绘制其位移(角位移)变化同力(力矩)之间的曲线,并与试验结果进行了对比,x方向和偏转方向的对比结果如图5 所示,横向y和z以及3 个偏转方向的对比曲线是类似的。对比结果表明:对接机构详细模型的整机性能仿真结果与试验结果从数值和趋势上一致性很好,可以在侧向再对接过程中使用对接机构六维非线性简化模型,性能参数使用试验值或仿真值都可以。
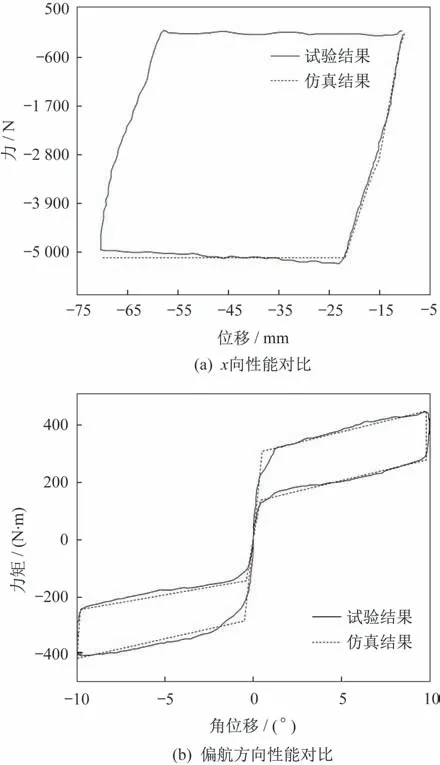
图5 对接机构整机性能Fig.5 Overall performance of the docking mechanism
1.2 对接机构简化建模方法
根据对接机构详细模型的整机性能曲线与工程实践结果,建立对接机构的简化模型。
1.2.1 纵向模型
对接机构纵向即x向模型如图6 所示,该性能曲线是分段线性函数,可表示为式(4)和式(5)。
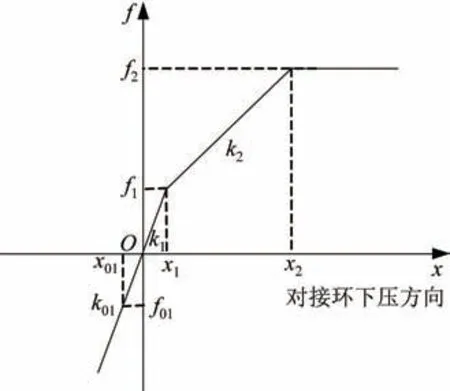
图6 对接机构纵向性能Fig.6 Axialperformance of the docking mechanism
其中,对接机构纵向受压时,受到的缓冲系统等效纵向缓冲力为
式中:f为对接环纵向受到对接机构弹簧阻尼等效的缓冲作用力;x为对接环纵向的运动位移变化量;x01、x1、x2为对接环纵向的运动位移特征区间值;f01、f1、f2为对接环在不同下压位移区间的力特性系数;k01、k1、k2为对接环在不同受拉或下压位移区间的刚度特性系数,可以通过力和位移参数表示,不是独立参数。
对接机构受拉时,受到的缓冲系统等效纵向缓冲力为
1.2.2 其他方向模型
对接机构的横向和角度偏转方向的模型和性能曲线类似,原理如图7 所示,以偏航为例。其中,φ是对接环偏航方向的运动角位移,φ1、φ2、φ3、φ4是对接环偏航方向的运动位移特征区间值,M1、M2、M3、M4是偏航方向角位移特征区间的力矩特性系数。滚转俯仰和横向方向的性能与偏航类似,数值不同见表1。
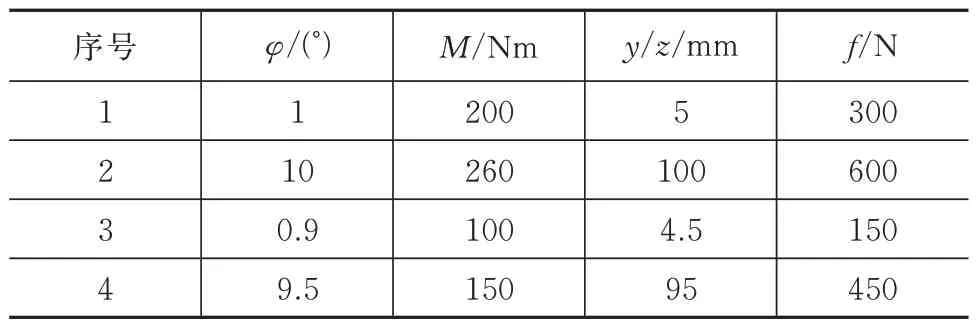
表1 与图7 对应的弹簧特性Tab.1 Spring characteristics corresponding Fig.7
当>0 时,
图7 与式(6)、式(7)、式(8)是对应的。
表1 和表2 的弹簧特性参数既是对接机构整机仿真模型的计算结果,也是对接机构简化模型的输入值,表1 中的φ和M的关系是3 方向偏转的特性参数值,y/z和f的关系是2 横向平移方向的特性参数值,表2 是纵向x方向的特性参数值。

表2 与图6 对应的弹簧特性Tab.2 Spring characteristics corresponding to Fig.6
表1 中的序号1~4 与图7 中的下标有对应关系,负方向特性关于原点反对称。
表2 中的序号1~4 与图6 中坐标轴横轴从左到右依次对应。
2 简化模型在侧向再对接中的应用
2.1 转位机构辅助实验舱侧向再对接模型
沈晓鹏、刘艳[26]论述了和平号和中国空间站转位组建方案,无论是翻转转位组建还是平面转位组建,其中,侧向再对接都是组建中一个重要的动力学过程。
侧向再对接捕获过程与通常的轴向对接捕获缓冲过程相同之处是:都需要对接机构的捕获锁实现捕获,捕获过程中丝杠联系组合,丝杠安装组合、差动组合等捕获缓冲系统工作原理相同。不同之处是:轴向对接的动力源自空间两飞行器存在相对运动速度产生的能量,惯性较大,捕获时间较短,而侧向再对接动力是对接机构电机以匀速缓慢推出对接环直到捕获安装在节点舱侧向口被动对接机构的导向板,惯性较小,捕获时间较长。
侧向再对接仿真模型如图8 所示,通过Adams软件建立转位机构辅助实验舱侧向再对接模型,模型主要包括实验舱、实验舱对接机构、核心舱、核心舱对接机构、转位机构;实验舱对接机构包括主驱动、主动对接环、捕获锁;核心舱对接机构主要包含被动对接环和卡板器;转位机构包括转位机构转臂、转位机构肩关节弹簧阻尼机构。主驱动实现匀速推出对接环的运动,对接环与实验舱之间是对接机构简化模型,实现对接环的6 自由弹性缓冲作用,3 把捕获锁均布在对接环周边,实现捕获卡板器的捕获功能,转位机构的肩关节弹簧阻尼机构与对接机构协同运动,提供侧向再对接过程的支撑连接,共同实现侧向再对接。
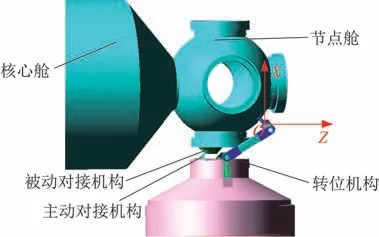
图8 侧向再对接仿真模型Fig.8 Simulation model of lateral re-docking
2.2 仿真结果及与试验结果的对比
应用转位机构辅助实验舱侧向再对接的动力学模型进行仿真,环推出速度3 mm/s,转位机构肩关节弹簧刚度350 N·m/°,阻尼3 500 N·m/((°)·s-1),对接机构y和z向阻尼1 200 N/(m·s-1),偏转方向阻尼10 N·m/((°)·s-1)。如图9 所示,主要方向的仿真结果与全时序试验台试验结果进行对比,其中横轴均为时间,主要考察了转位机构辅助再对接过程中的对接机构和转位机构的运动,以及对核心舱的干扰力和力矩,力和力矩方向如图8 所示。
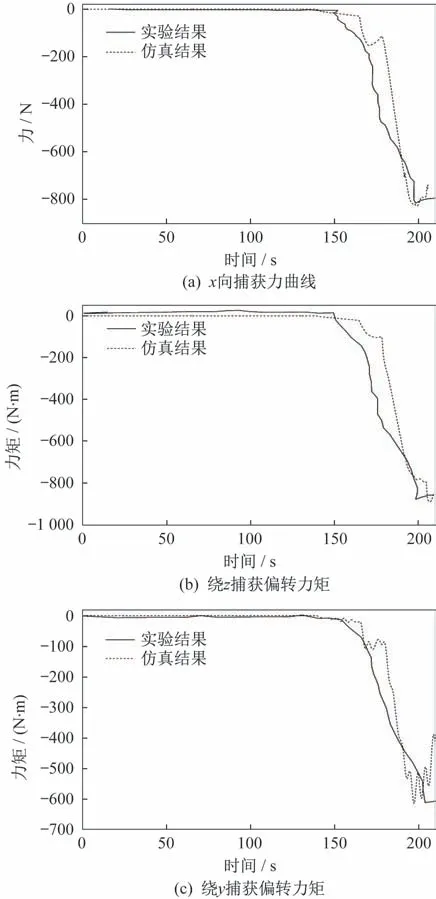
图9 仿真与试验结果对比Fig.9 Comparison of the simulation and test results
图9(a)是x向对接力的仿真与试验结果对比,图9(b)是绕z向偏转力矩的仿真与试验对比结果,峰值约810 N·m,图9(c)绕z向偏转力矩的仿真与试验对比结果,峰值约600 N·m,数值和趋势一致性较好。仿真与试验不仅对比了对接环捕获力和力矩结果,也对比了对接环典型运动方向的位移和角位移结果。
仿真与试验的对接环z向运动位移、绕y向角位移以及转位机构肩关节的角位移对比结果见表3,误差最大值约8%,仿真与试验结果一致性较好,数据有效,可以作为组建过程流程设计的依据。

表3 仿真与试验的运动结果对比Tab.3 Comparison of the simulation and test results
3 结束语
文章以异体同构周边内翻式对接机构为研究对象,建立了简化的对接机构缓冲系统模型,在此基础上,进行了简化模型的应用研究,建立了转位机构辅助实验舱侧向再对接仿真模型,给出再对接过程仿真的运动学和动力学结果。仿真结果与试验结果的数值和趋势一致性较好,运动量对比结果误差小于10%,结果可以作为组建过程流程设计的依据。
这种复杂机构动力学简化方法对于其他复杂机构也有借鉴意义,有助于开展全面的动力学过程研究。
