载人航天器太阳翼多姿态输出能力建模及分析

杨永淼，葛茂艳，周 妍，刘必海，张亚鹏

（上海空间电源研究所，上海 200245）

0 引言

我国天宫空间站实验舱电源系统采用双自由度对日定向设计［1］，太阳电池翼具有2 个互相正交的旋转轴，实现2 个维度的对日定向。α轴补偿航天器轨道角的变化，β轴补偿太阳高度角的变化［2］。双自由度对日定向转动方案理论上可在光照区保证太阳光垂直入射，使得太阳电池在整个光照区始终具有最佳的光照条件，进而最大化利用太阳翼的发电能力［3］。

根据在轨实际任务的需要，太阳翼除了处于转动对日定向工作状态外，还可能处于α轴特定位置停转的复杂工作状态［4-16］。在“组合体径向交会对接与撤离”和“功率通道长期低负载运行”等工作模式下，太阳翼将长时间处于α轴水平归零的工作状态，在“组合体轴向交会对接与撤离”“组合体轨控”等工作模式下，太阳翼将长时间处于α轴垂直归零的工作状态。

在α轴水平归零或垂直归零状态下，光照区内太阳入射角无法保持固定不变，而是随着轨道角变化而变化。这使分析太阳翼在轨发电能力和计算电源分系统能量平衡变得复杂［11，17-18］。但在实际飞行任务中，为了保证空间站能源充足安全的能源供应，准确预测太阳翼发电能力是有必要的。

为了准确预计太阳翼发电能力的变化情况，合理规划各项在轨任务的具体方案，防止供电不足导致出现蓄电池组过放、功率通道断电等严重后果［12］，需要对太阳翼α轴水平归零和垂直归零工作模式下在轨发电能力随太阳高度角和β轴转角的变化规律展开研究。建立太阳入射角与轨道角、β轴转角和太阳高度角的数学模型，推导出太阳入射角在1 个轨道周期内，随太阳高度角和β轴转角的变化关系。将分析结果与光照区时长的计算相结合，给出太阳翼发电能力的理论波形，并将其与实际在轨飞行数据展开比对分析。结果表明，分析结果合理，与实测数据相符，可将其作为预测复杂工作模式下太阳翼发电能力的理论工具。

1 建模对象介绍

1.1 空间站双自由度对日定向构型

空间站飞行轨道为340～450 km 近圆轨道，三舱组合体主要以三轴对地姿态飞行［19］。在1 个地球公转周期内，空间站轨道面太阳高度角在-66°～66°范围内变化。空间站太阳电池翼具备双自由度对日定向功能，如图1 所示。太阳翼在α 自由度上具备360°连续转动能力，在β自由度上具备-180°～180°摆动能力［20］。

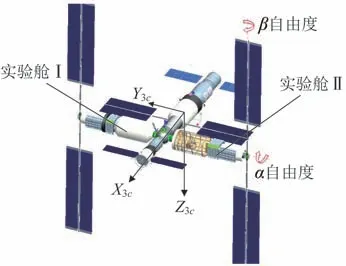
图1 空间站双自由度对日定向构型Fig.1 Two-degree-of-freedom sun-pointing configuration of the space station

空间站组合体太阳翼正常对日定向时，α轴以轨道角速度做360°匀速圆周运动，以补偿轨道角变化对太阳入射角的影响。β轴随着太阳高度角的变化在-66°～66°范围内摆动，以补偿太阳高度角对太阳入射角的影响。

1.2 特殊任务下的太阳翼姿态

组合体在轨飞行时一般处于太阳翼双自由度对日定向转动工作状态，以保证太阳入射角始终最小，太阳翼始终以最大功率输出电流，为整舱提供尽可能多的能量供应［21-23］。但在特殊的对接、轨控等飞行任务中，太阳翼可能处于在对日定向转动以外的工作状态。

1.2.1 组合体与载人飞船径向交会对接/撤离

在组合体与载人飞船径向交会对接或撤离任务中，载人飞船从组合体下方接近或远离节点舱对接口。为使帆板避开载人飞船对接路径，保证任务过程中太阳翼与飞船之间具有足够的安全距离，同时降低帆板承受的冲击载荷［5］，在任务过程中帆板处于α轴水平归零、β轴垂直归零的工作状态。

1.2.2 组合体与来往飞行器轴向交会对接/撤离

在组合体与载人飞船、货运飞船等来往飞行器轴向交会对接或撤离任务中，来往飞行器与组合体共轨飞行，沿核心舱轴线方向接近或远离对接口。为在来往飞行器对接和撤离路径上保留充分的安全距离，减少发动机羽流对帆板施加的载荷，在任务过程中，太阳翼处于α轴垂直归零、β轴固定角度伺服的工作状态。

1.2.3 轨道机动控制

在轨控任务中，轨控发动机开机，沿核心舱轴向对组合体施加推力［6］。为使太阳翼避开发动机羽流路径，减少羽流对太阳翼施加的作用力，降低太阳翼迎风面积［21-22］，在任务过程中，太阳翼处于α轴垂直归零、β轴垂直归零的工作状态。

1.2.4 功率通道长期轻载工作

在功率通道长期处于负载较轻的工作状态时，为减少α轴对日定向机构磨损，将帆板设置为α轴水平归零，β轴对日固定角度伺服的工作模式。在帆板发电量满足功率通道负载需求的前提下，降低对日定向装置机构运行圈数，进而减少机构传动链路上各个部件的磨损和变形，延长对日定向装置在轨工作寿命。

在以上4 种特殊飞行任务中，出于安全避让、规避发动机羽流、避免遮挡数传天线、减少驱动机构磨损、降低太阳翼承受的力学载荷等目的，太阳翼较长时间工作在α轴水平归零或垂直归零的工作状态［24-25］。在该工作模式下，太阳翼无法时刻保持对日定向，太阳入射角将随着轨道角∠α、太阳高度角∠β、β轴转角∠β′的变化而变化［13］。在1 个轨道周期内，太阳翼输出电流波形不是近似直线，而是随轨道角度变化的曲线［14-16］。为实现保障飞行过程中能源供应可靠稳定，实现在轨能量平衡，需准确预计具体工作条件下的太阳翼发电量，进而合理设计任务实施方案和规划工作流程。将对太阳翼的太阳光入射角建立数学模型，对α轴水平归零和垂直归零工作模式下的发电量展开分析计算。

2 建立入射角模型

2.1 太阳翼α 轴水平归零入射角建模及分析

2.1.1 建立太阳翼α轴水平归零太阳入射角模型

建立太阳翼水平归零状态下入射角的几何模型，如图2 所示。

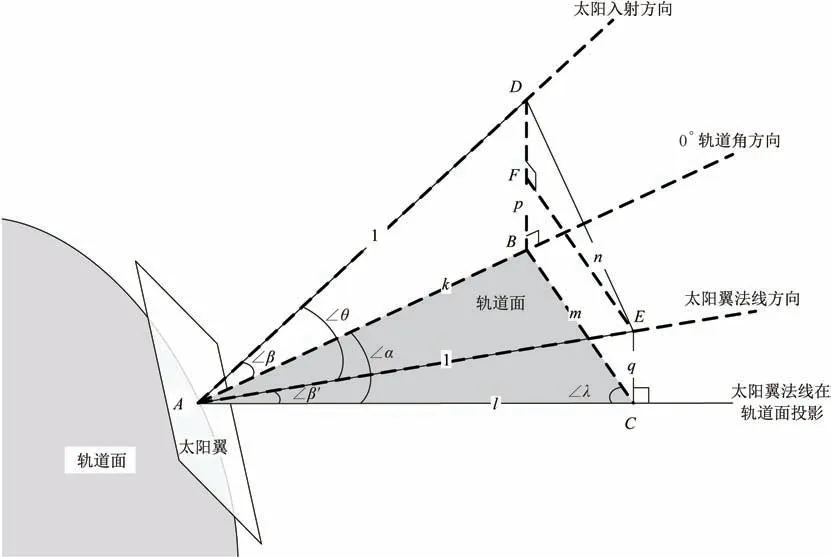
图2 太阳翼水平归零太阳入射角模型Fig.2 Solar incidence angle model when the solar wings are at the horizontal state

其中，航天器轨道角∠α为地球质心与航天器的连线在黄道面的投影与地日连线的夹角［7］。当地球质心与航天器的连线在黄道面的投影指向太阳时，定义α角为0°。1 个轨道周期内∠α在-180°～+180°范围内变化。

α轴转角∠α′为太阳翼在α自由度上的转动角度。太阳翼α轴对日定向转动状态下，航天器处于轨道角为0°时的∠α′定义为0°。∠α′可在0°～360°范围内变化。

太阳高度角∠β为日地连线与轨道平面的夹角，其在±（i+γ）间变化，i是以赤道面为参考平面的轨道倾角，γ为黄赤夹角（23.45°）。

β轴转角∠β′为太阳翼在β自由度上的转动角度。定义太阳翼处于布片面法线沿地球与航天器连线指向太空时的∠β′为0°。β′角可在-66°～+66°范围内变化。

太阳入射角∠θ为太阳光对太阳电池阵的入射角，即太阳翼布片面法线与太阳入射矢量的夹角。∠θ在0°～180°范围内变化，0°≤∠θ≤90°时，表示太阳照射太阳翼正面；当90°≤∠θ≤180°时，表示太阳照射太阳翼背面。可通过倾斜太阳翼使太阳光直射，太阳翼电能的产生与光强矢量在太阳翼法线方向的分量成正比，即与cos∠θ成正比；当∠θ=0°时，所产生的电能最大；当∠θ=90°时，无电能产生［8］。

太阳翼随航天器沿飞行轨道绕地飞行，0°轨道角方向即地日连线在轨道面的投影。太阳入射方向与轨道面的夹角为太阳高度角∠β。太阳翼法线方向随太阳翼转动角度变化而变化。由于α轴保持水平归零，太阳翼法线仅在β自由度平面内转动。太阳翼法线方向轨道面作投影，太阳翼法线与投影之间的夹角即为β轴转角∠β′。太阳翼法线在轨道面的投影与0°轨道角方向即为轨道角∠α。太阳入射角∠θ定义为太阳光对太阳电池阵的入射角，通过理论推导，可得到入射角∠θ与轨道角∠α、太阳高度角∠β和β轴转角∠β′之间的数学关系。

根据图2 所示模型，以太阳入射点为原点，取太阳入射角方向和太阳翼法线方向线段长度为1。将2 条线段末端相连，得到线段n。线段n在轨道面的投影为线段m。线段n与线段m所在的平面在0°轨道角方向截取线段k，在太阳翼法线投影上截取线段l。

2.1.2 太阳翼α 轴水平归零太阳入射角分析

由于△ADB和△AEC为直角三角形，因此p=sin∠β、q=sin∠β′。从E点向m作垂线，垂足为F。由于线段EF平行于线段m，因此可得线段DF表达式如下：

在直角三角形△DEF内可得表达式如下：

在△ABC内，根据正弦定理可得表达式如下：

根据式（4）、式（5）可得线段m表达式如下：

直角三角形△DEF的3 条边满足下式：

由式（1）可做如下推导：

联立式（8）和式（9）：

联立式（4）～式（6），∠λ可由∠α、∠β和∠β′表示，推导过程如下：

综上可得太阳翼α轴水平归零太阳入射角∠θ的表达式如下：

2.2 太阳翼α 轴垂直归零入射角建模及分析

2.2.1 建立太阳翼α轴垂直归零太阳入射角模型

由于α轴保持垂直归零，当飞行器所在的轨道角为∠α时，太阳翼沿轨道前进方向旋转了90°，因此太阳翼法线在轨道面投影与轨道角∠α保持90°夹角。太阳翼法线在轨道面投影所在的角度为∠α+90°。太阳翼β轴在转角在垂直于轨道面的方向上变化。

建立太阳翼α轴垂直归零状态下入射角的几何模型如图3 所示。太阳翼以太阳入射点为原点，取太阳入射角方向和太阳翼法线方向线段长度为1。将2 条线段末端相连，得到线段n。线段n在轨道面的投影为线段m。线段n与线段m所在的平面于0°轨道角方向截取线段k，于太阳翼法线投影上截取线段l。太阳翼法线在轨道面的投影与航天器轨道角方向垂直。

图3 太阳翼垂直归零太阳入射角模型Fig.3 Solar incidence angle model when the solar wings are at the vertical state

通过理论推导可得，入射角∠θ与轨道角∠α、太阳高度角∠β和β轴转角∠β′之间的数学关系。

2.2.2 太阳翼α轴垂直归零太阳入射角分析

太阳翼α轴垂直归零工况下，太阳入射角数学模型与水平归零工况下类似，仅需将太阳翼法线在轨道面的投影与0°轨道角方向的夹角由∠α替换为∠α+90°。

根据式（10）和式（11）可得，太阳翼α轴垂直归零太阳入射角∠θ的表达式如下：

2.3 光照区轨道角度

太阳翼的输出能力除了与太阳入射角度有关外，还受到光照区时长的影响。仅当航天器处于光照区，且太阳入射角小于90°时，帆板正面才可接收到太阳光照射，进而输出电能。因此为了准确地计算航天器太阳翼在轨输出能力，还需要计算航天器进光照区时刻和出光照区时刻对应的轨道角。

由于空间站飞行轨道为近地圆轨道，可近似地射向地球的太阳光看作平行光，地影模型为圆柱型地影模型［9-10］，如图4 所示。

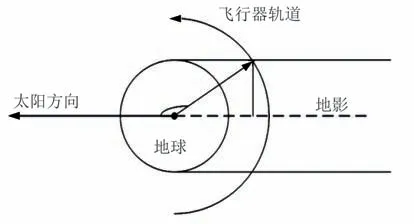
图4 地影模型Fig.4 Earth shadow model

不同太阳高度角下，进、出光照区时刻对应的轨道角见表1。

表1 航天器进、出光照区轨道角Tab.1 Orbital angles of the spacecraft entering and exiting the illumination region

3 仿真分析

3.1 轴对地飞行姿态

空间站三舱组合体在轨长期处于三轴对地姿态，如图5 和图6 所示。图5 中实验舱太阳翼α轴处于水平零位，图6 中实验舱太阳翼α轴处于垂直零位。

图5 站组合体三轴对地姿态太阳翼α 轴水平归零Fig.5 Three-axis attitude of the station assembly to the earth when the α-axis of the solar wing is at the horizontal state

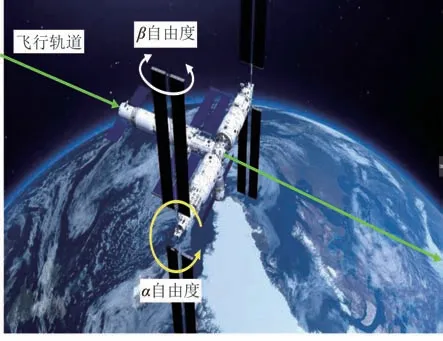
图6 空间站组合体三轴对地姿态太阳翼α 轴垂直归零Fig.6 Three-axis attitude of the station assembly to the earth when the α-axis of the solar wing is at the vertical state

3.2 太阳翼α 轴水平归零模式仿真

根据理论计算结果，设置几组模型参数，对太阳翼α轴水平归零时，1 个轨道周期内太阳入射角和帆板发电量随轨道角变化的波形展开分析。太阳入射角小于90°时，表示太阳光照射帆板正面；太阳入射角大于90°时，表示太阳光照射帆板背面。模型参数设置情况如下。

1）板转角∠β′为0°，太阳高度角∠β在0°～60°范围内变化。

2）帆板转角∠β′为20°，太阳高度角∠β在0°～60°范围内变化。

3）帆板转角∠β′为40°，太阳高度角∠β在0°～60°范围内变化。

4）帆板转角∠β′为60°，太阳高度角∠β在0°～60°范围内变化。

太阳翼α轴水平归零时，“太阳入射角-轨道角”曲线和“太阳翼输出电流-轨道角”曲线如图7、图8所示。由图7 和图8 可得，太阳入射角和帆板输出电流符合如下规律。

图7 “太阳入射角-轨道角”曲线-α 轴水平归零Fig.7 Calculated solar incidence angle when the α-axis of the solar wing is horizontal

图8 “太阳翼输出电流-轨道角”曲线-α 轴水平归零Fig.8 Calculated output capacity of the solar wing when the α-axis of the solar wing is horizontal

1）当帆板转角∠β′＝0°，随着太阳高度角增加，太阳光最大入射角增大。

2）当帆板转角∠β′＝0°，即太阳平行轨道面入射时，太阳光照射阵面正面的时间始终占1/2 轨道周期，不受帆板转角的影响。

3）帆板转角∠β′≠0°时，太阳光照射阵面正面的时间随帆板转角∠β′的增大而增大，实际受晒时间长于1/2 轨道周期。

4）随着帆板β轴朝向对日定向方向转动，太阳光最大入射角相应减小，最大入射角＝0°－∠β+∠β′。帆板输出电流正比于入射角余弦值，随着入射角度的增大而降低。因此，在太阳翼α轴水平归零、帆板β轴对日定向的情况下，随着太阳高度角增大，帆板最大入射角减小，受晒时间增大，帆板输出能力相应增大。

5）由图8 可知，在太阳翼α轴水平归零、帆板β轴对日定向的情况下，帆板输出能力随太阳高度角的变化而受光照区时长的制约。进入阴影区后，太阳翼的输出能力降低至0。

3.3 太阳翼α 轴垂直归零模式仿真

根据理论计算结果，设置几组模型参数，对太阳翼α轴垂直归零时，1 个轨道周期内太阳入射角和帆板发电量随轨道角变化的波形展开分析。模型参数设置情况如下。

1）帆板转角∠β′为0°，太阳高度角∠β在0°～60°范围内变化。

2）帆板转角∠β′为20°，太阳高度角∠β在0°～60°范围内变化。

3）帆板转角∠β′为40°，太阳高度角∠β在0°～60°范围内变化。

4）帆板转角∠β′为60°，太阳高度角∠β在0°～60°范围内变化。

太阳翼α轴垂直归零时，“太阳入射角-轨道角”曲线和“太阳翼输出电流-轨道角”曲线如图9 和图10 所示。

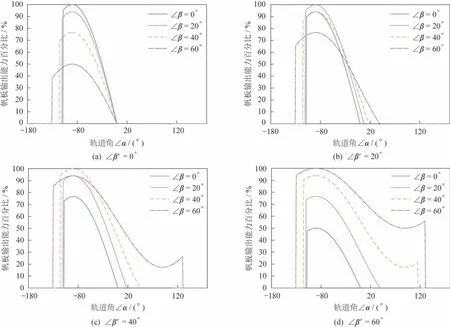
图10 太阳翼α 轴垂直归零工况下计算得到的帆板输出能力Fig.10 Calculated output capacity of the solar wing when the α-axis of the solar wing is vertical

太阳入射角和帆板输出电流符合如下规律：

1）帆板β轴转角∠β′为0°时，以光照区中点为界，光照区前半段太阳入射角<90°，阳光照射帆板正面，后半段太阳入射角>90°，阳光照射帆板背面。

2）随着太阳高度角∠β的增大，阳光最大入射角增大，帆板最大输出功率相应降低。随着∠β的增大和帆板转角∠β′得到增大，帆板正面受晒时间逐渐增加。

3）在阴影区，理论上太阳入射角<90°，但受地球阴影遮挡，帆板发电量为0。

4 在轨数据验证

α轴水平归零工况下的太阳翼输出电流实测波形如图11 所示。该工况下太阳高度角为37.8°，太阳翼处于α轴水平归零，β轴转角40°。经与仿真波形比对，实测数据与理论分析结果基本一致。入射角较大时，帆板实际发电效率略微降低［23］，因此轨道角较大时，帆板实际功率输出能力略低于理论值。

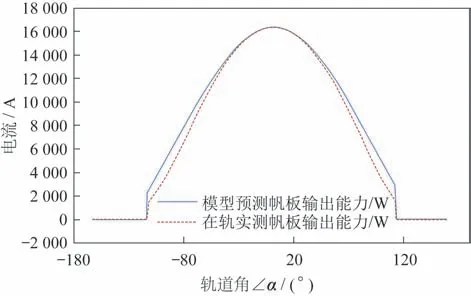
图11 α 轴水平归零工况下实测的太阳翼电流Fig.11 Measured output capacity of the solar wing when the α-axis of the solar wing is horizontal

α轴垂直归零工况下的太阳翼输出电流实测波形如图12 所示。该工况下的太阳高度角为1.87°，太阳翼处于α轴垂直归零，β轴转角0°。经与仿真波形比对，实测数据与理论分析结果基本一致。光照区后半段太阳光照射帆板背面，由于受到地球红外返照和舱体反射光线的影响，帆板仍可输出较小电流。

图12 α 轴垂直归零工况下实测的太阳翼电流Fig.12 Measured output capacity of the solar array when the α-axis of the solar wing is vertical

5 结束语

载人航天器太阳翼在轨运行期间，除正常对日定向转动外，根据任务要求，需要工作在α轴水平归零或垂直归零等特殊状态。在特殊工作模式下，太阳入射角和太阳翼输出能力变化曲线更加复杂，难以预计。本文建立太阳入射角与轨道角、太阳高度角、β轴转角等变量的数学模型，从理论上推导太阳入射角的变化规律，并结合光照区时长，建立太阳翼在轨输出能力的预测模型。经与实际飞行数据比较，可知该模型能较为准确地评估特殊工作模式下太阳翼的输出能力，为整舱在轨能量平衡分析和飞行任务计划安排提供新的工具。但在建立模型时，未考虑舱体和其他舱段太阳翼对分析目标的遮挡及地球红外返照，如存在互相遮挡，且其光照和遮挡情况较为复杂，需结合实际情况进一步分析。