基于CFD 方法的十字形降落伞–航行体系统数值分析

耿文豹，周 石，洪树峰，黄佳进

（汕头大学 工学院，广东 汕头 5150631）

0 引言

自主水下航行器（AUV）是一种非系留移动平台，用于海洋科学家、海洋工业和军事的调查作业。为了提高AUV 的部署效率和能力，通过载机在特定海域内对AUV 进行低空空投布放，可以大大缩短任务时间，提高任务效率[1]。为了保证AUV 的入水姿态及速度符合入水速度要求，就必须依靠降落伞装置对AUV 进行姿态控制及稳定减速。十字（或十字形）降落伞由于其相对较高的阻力系数和较低的制造成本，广泛应用于低空空投减速过程[2]。

目前国内外对物伞系统的数值分析研究主要采用2 种技术路线：一种是计算流体力学（CFD）方法，该方法可研究在稳降阶段时降落伞系统的流场分布规律及气动特性[3-5]；另一种是流固耦合（FSI）法，反应其非定常流场和柔性降落伞衣相互作用机制，在伞衣充气涨满阶段常用此方法[6-9]。上述文献中只是对单一圆形伞衣或者尾流进行流场与气动特性的分析，没有对用于低空减速的十字形伞-物系统进行研究，同时拖曳距离对降落伞的具体影响不够详细。

因此本文基于Realizablek–ε湍流模型，采用数值计算的方式，以十字形降落伞–航行体系统为研究对象，探讨不同拖曳比下十字形降落伞–航行体系统的流场分布规律及十字形降落伞衣与航行体的气动特性变化。

1 数值计算方法

1.1 控制方程

质量守恒方程：

式中：ρ为密度；t为时间；μ，ν，ω为速度分量。

动量守恒方程：

式中：p是流体微原体上的压力；τxx，τyz，τzx是黏性应力τ的分量；Fx，Fy，Fz是微原体上的体力，若只有重力且z轴竖直向上，则Fx=0，Fy=0，Fz= –ρg。

1.2 湍流模型

Realizablek-ε湍流模型：

式中：k，ε分别为湍动能方程、湍动能耗散率方程；ρ为密度；μ为动力黏度；υ为运动黏度；ui为速度沿i方向分量；xi，xj分别为向量沿i，j方向分量；E为时均应变率；Gk为时均速度引起湍动能k的产生项。

经验系数：σk＝1.0；σε＝1.2；C2＝1.9。

采用MUSCL 三阶格式进行流场方程离散，利用用PISO 算法，其中压力插值选择Standard 格式，为处理非定常计算的伪扩散问题选择Greed-Gauss Node-based 进行梯度插值[10]。

2 模型验证

为了验证本文数值模型的可行性与准确性，首先对如图 1 所示的十字形降落伞开展非定常数值计算。

图1 十字形伞模型Fig. 1 Cross parachute mode

流场计算域如图2 所示，采用速度入口与压力出口，伞衣与流场边界为无滑移壁面，流场网格类型为非结构化四面体网格，伞衣表面为三角形网格。

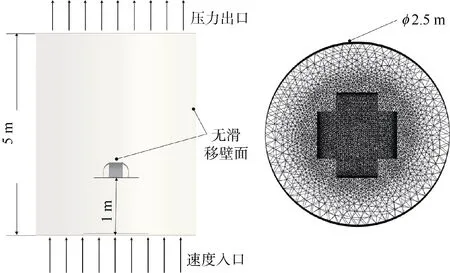
图2 流场计算域Fig. 2 Computational domain of flow field

模型对比如表1 所示（本节使用的模型简称为A 模型，文献[11]建立的模型简称为B 模型）。

表1 模型对比Table 1 Model comparison

图3（a）为十字形伞速度矢量图，伞衣顶部尾流区域的出现一对大小相等，方向相反的涡流。放大图如图3（b）。在图4 中绘制了流场可视化图像。伞衣表面为压力云图。

早期典型的干法回收锂电池中有价金属的工艺过程为：先拆解电池除去外壳，获取电极材料，加入焦炭、石灰石混合均匀后高温焙烧，有机物燃烧后转化为二氧化碳及其他气体，氟和磷形成沉渣，铝被氧化成炉渣，锂大部分以氧化锂气体蒸气溢出，金属 Cu、Co、Mn、Ni等形成碳合金[5]，工艺流程如图4所示。

图3 涡流区域Fig. 3 Vortex flow region

图4 流场可视化Fig. 4 Flow field visualization

模型A 数值计算结果均与模型B 结果吻合，本文数值模型有效。

3 研究对象及仿真内容

十字形降落伞–航行体系统模型如图5 所示。直径D=200 mm，高La=1 200 mm，拖曳比λ=H/La，分别为1、2、3、4，攻角α=0°。大气条件为高度300 m，来流速度v=30 m/s。为获得准确的流场变化，本文采用适用于绕流物体的非结构四面体网格，同时对核心的流场网格进行加密，流场网格数为5 307 044 个，数值模型如图6 所示。流场计算域为与航行体轴线重合的圆柱体，计算域直径为6D，高度为10D。边界条件为速度进口和压力出口，降落伞衣面及航行体为无滑移壁面。

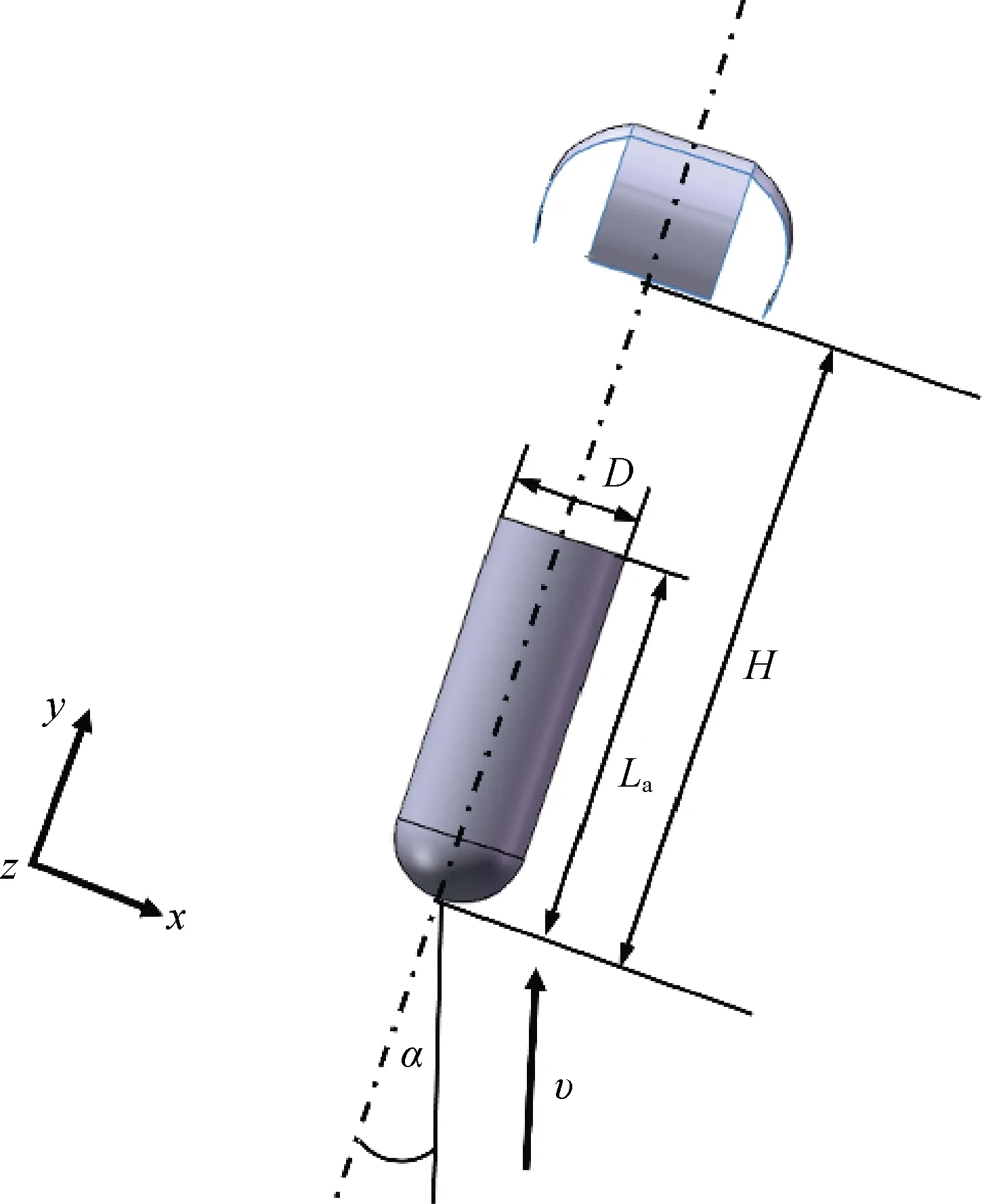
图5 十字形降落伞–航行体系统模型Fig. 5 Cross parachute-underwater vehicle system model

图6 数值模型Fig. 6 Number model

针对十字形降落伞与航行体系统，开展不同拖曳比的物伞系统绕流流场计算，做如下假设：1）不考虑降落伞伞绳对流场的影响；2）降落伞与航行体处于匀速稳定下降阶段，伞衣外形不变，不考虑降落伞衣织物透气性；3）降落伞衣充满外形为十字圆形，投影DT和名义直径D0的比取经验值0.7。

4 计算结果分析

4.1 流场分析

图7 显示不同拖曳比下十字降落伞–航行体系统的流场速度矢量图，图8 为速度云图。空气沿降落伞衣外缘气流流速明显高于降落伞衣顶部区域，在航行体尾部降落伞衣内部及降落伞衣顶部出现两个对称分布的漩涡区，随着拖曳比的逐渐增加（λ>2），漩涡区随之扩大并趋于稳定。

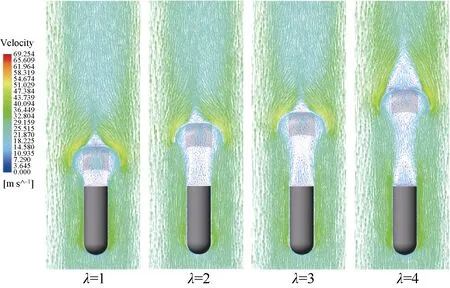
图7 速度矢量图Fig. 7 Velocity vector

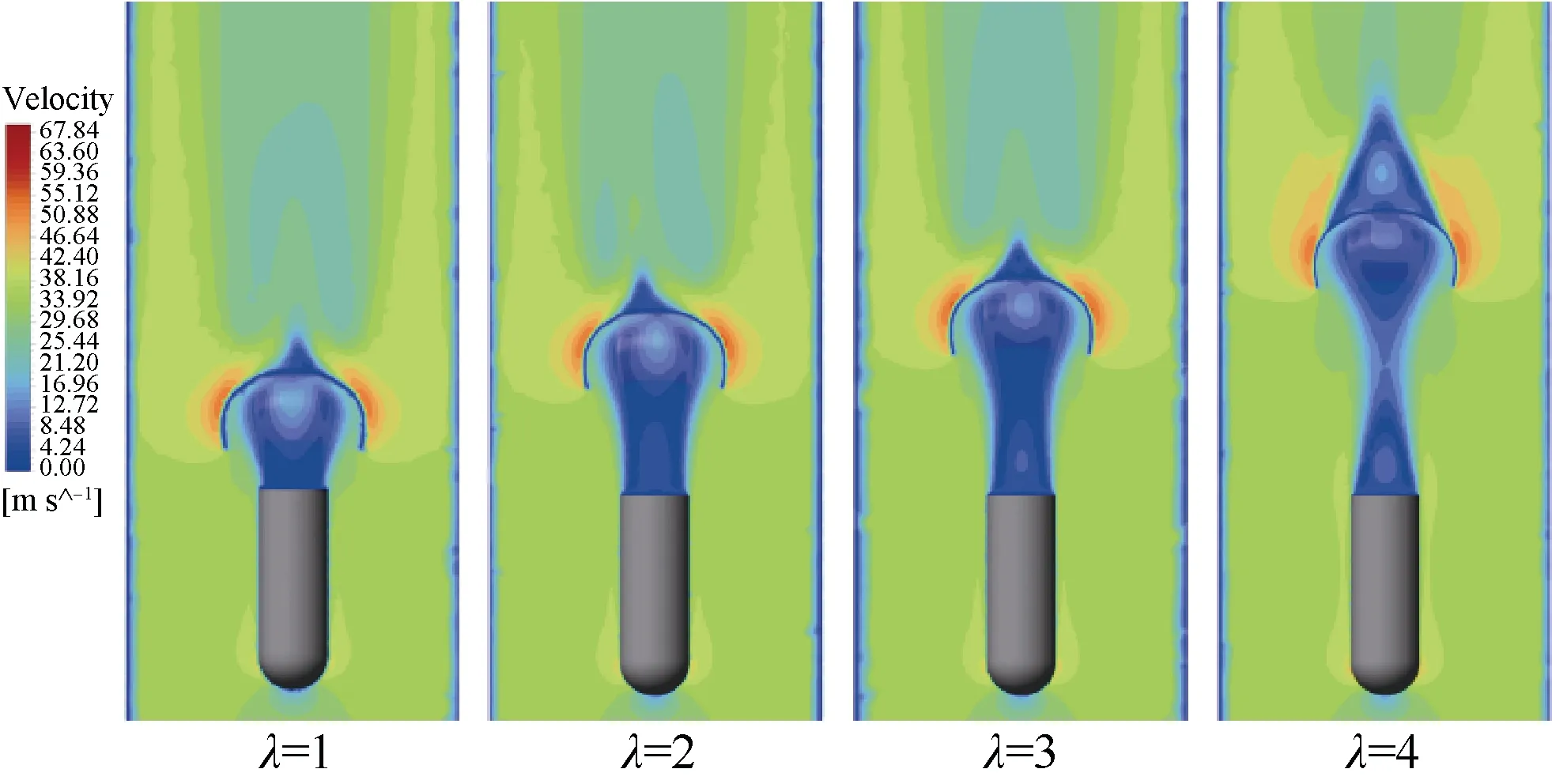
图8 速度云图Fig. 8 Velocity contour

图9 显示不同拖曳比下趋于稳定时十字降落伞–航行体系统的流场压力分布。可以看出，当拖曳比过小时（λ≤2），航行体阻挡了自由来流进入降落伞衣，航行体和降落伞衣形成闭式流动，降落伞衣内外压差极小，降落伞衣阻力损失严重；随着拖曳比增加（λ>2）逐渐转变为开式流动，十字形降落伞–航行体系统压力分布更为对称，十字伞衣内部形成稳定的正压区，顶部形成负压区。

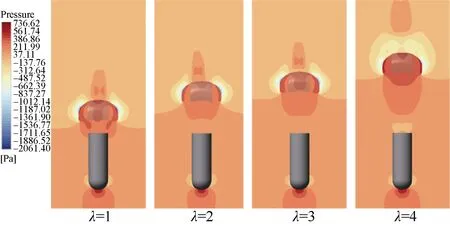
图9 压力云图Fig. 9 Pressure contour

4.2 气动特性分析

图10 和图11 显示不同拖曳比下降落伞衣入口与航行体尾部的压力监测。

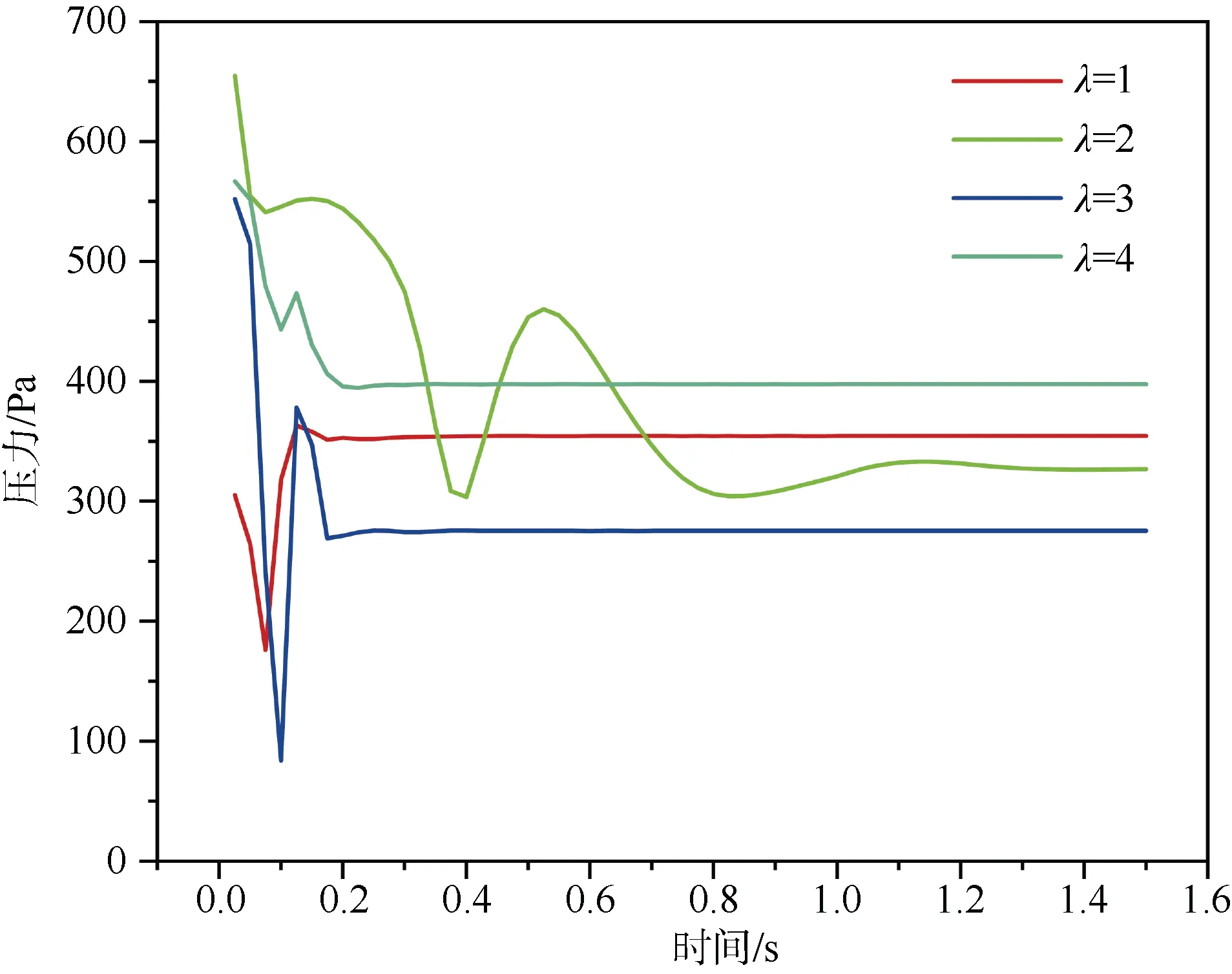
图10 不同拖曳比的十字形降落伞衣入口压力监测Fig. 10 Cross parachute inlet pressure monitoring with different towing ratios

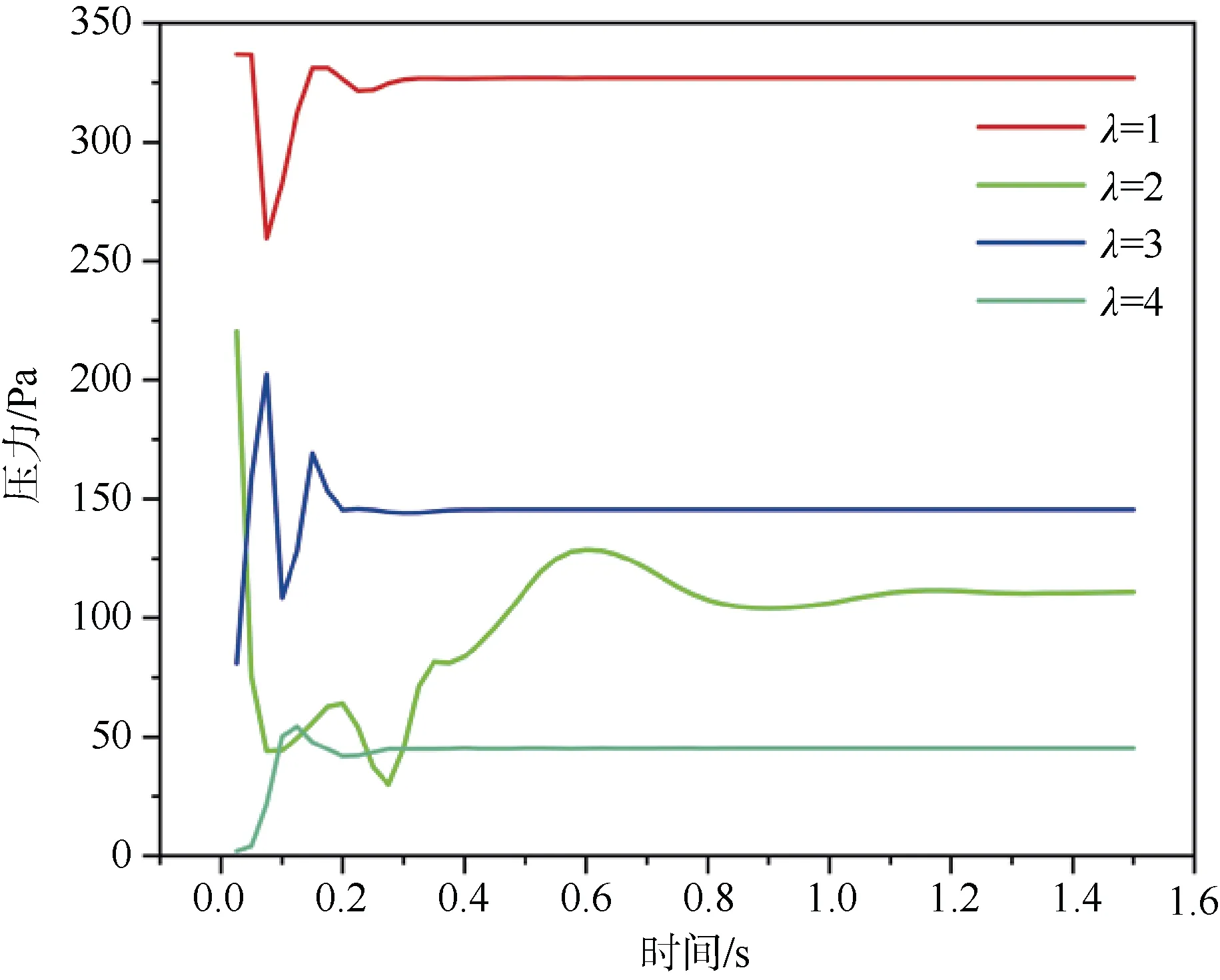
图11 不同拖曳比的航行体尾部压力监测Fig. 11 Underwater vehicle wake area pressure monitoring with different towing ratios

为了更直观地表现拖曳比对降落伞衣入口与航行体尾部压力的影响，定义Δp别为λ=1，λ=2 时，降落为降落伞衣入口与航行体尾部压力差值。从图12 可以看出，当拖曳比分伞衣入口与航行体尾部压力差值Δp分别为27 Pa、129 Pa，降落伞衣完全处于闭式流动。随着拖曳比增加（λ>2）），航行体尾部与降落伞衣入口处的压差Δp分别升高到209 Pa、352 Pa，降落伞处于开式流动，拖曳比λ最大时的压差Δp相较拖曳比最小时的压差增加了12%。

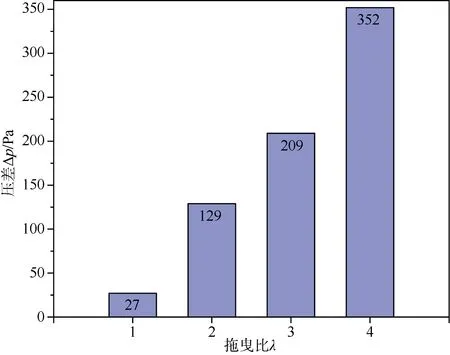
图12 不同拖曳比的降落伞衣入口与航行体尾部压力差值Fig. 12 Pressure differences between inlet of cross parachute and wake of underwater vehicle with different towing ratios

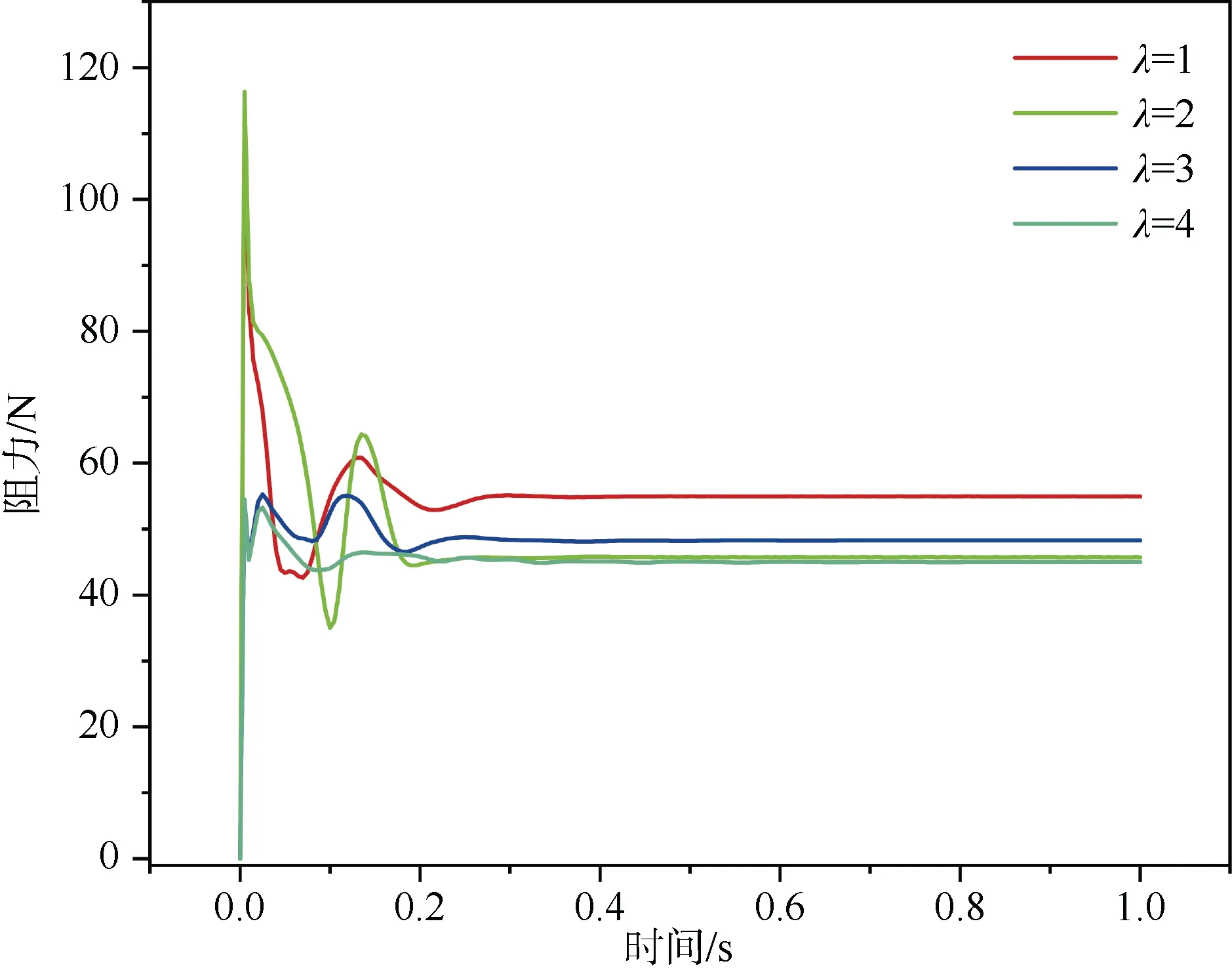
图13 不同拖曳比的十字形降落伞阻力变化Fig. 13 Cross parachute drag varying with different towing ratios

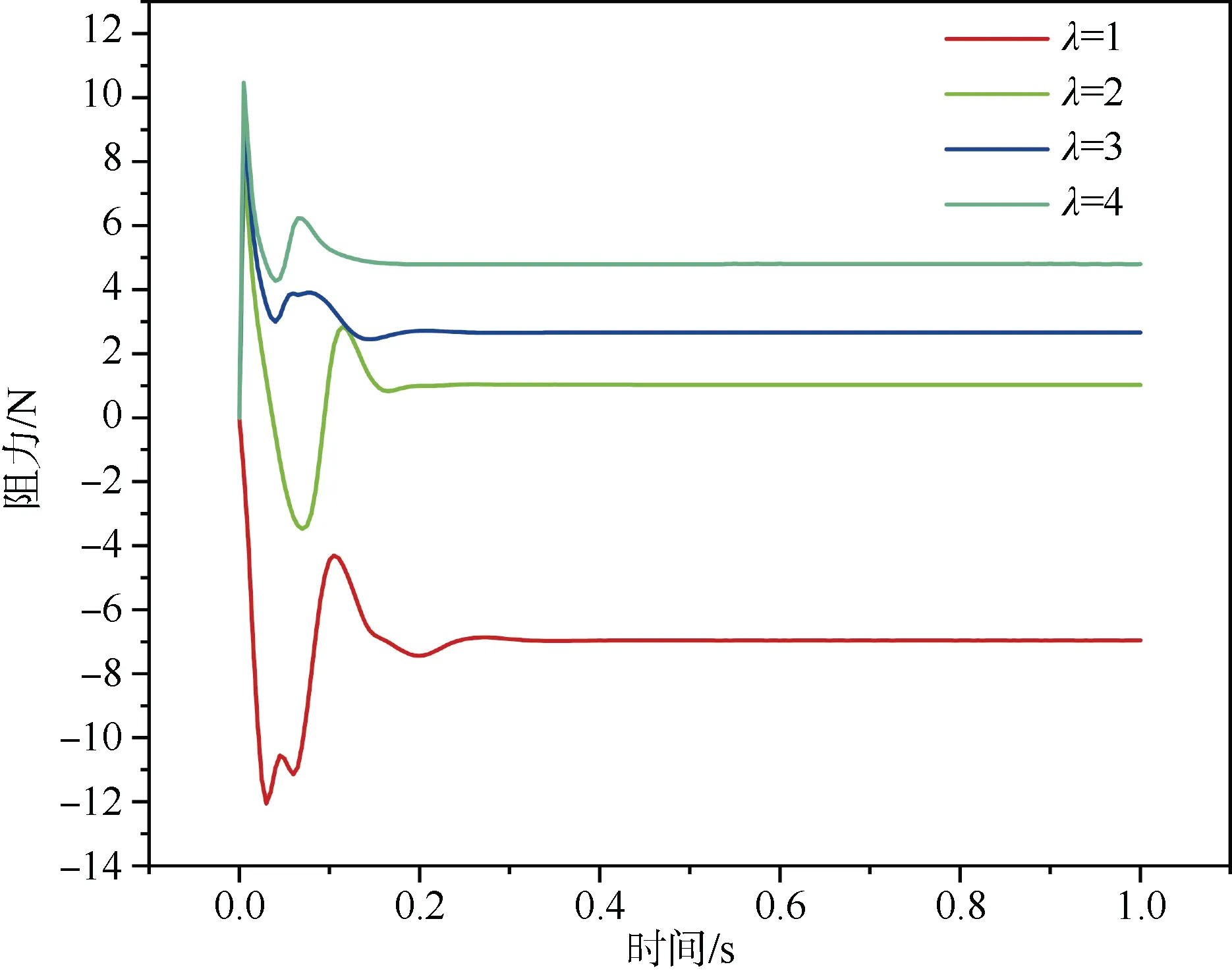
图14 不同拖曳比的航行体阻力变化Fig. 14 Underwater vehicle drag varying with different towing ratios

相较最小拖曳比的阻力，拖曳比λ=4 时，降落伞与航行体的阻力分别增加1.8%，25%，使得系统逐渐趋于稳定，气动特性处于最佳状态。

5 结论

为了探究在航行体对十字形降落伞工作性能的影响，本文开展了不同拖曳比下降落伞系统的数值研究，得出如下结论：

1）随着拖曳比的逐渐增加，降落伞衣内部及降落伞衣顶部两个对称分布的漩涡区扩大并趋于稳定。

2）当拖曳比过小（λ<2），航行体和降落伞衣形成闭式流动，降落伞衣阻力损失严重，随着拖曳比的增加，航行体尾流区的压力恢复，降落伞衣底部形成稳定的正压区，顶部形成稳定的负压。十字形降落伞–航行体系统的流场和压力分布更为对称。

3）当拖曳比过小（λ<2）时，降落伞与航行体阻力波动较大，且阻力有损失，随着拖曳比增加，降落伞与航行体阻力波动减小，降落伞处于开式流动，拖曳比λ最大时的压差Δp相较拖曳比最小时的压差增加了12%。

当拖曳比λ=4 时，降落伞与航行体的阻力分别增加1.8%，25%，航行体与降落伞工作稳定，气动特性处于最佳状态。

6 结束语

CFD 方法在研究稳降阶段的十字形降落伞–航行体系统的流场情况时，具有很好的准确性与真实性。其次，在确定最佳拖曳比的情况下，可开展不同攻角，不同外形尺寸的十字形降落伞–航行体系统的其它工况的研究，同时为十字形降落伞与航行体结构设计提供参考，为航行体的空投实验研究提供基础，具有指导工程实践的意义。在将来的研究中伞衣织物透气性及流场与伞衣形变的流固耦合作用会被进一步考虑。