单机动平台时差定位航路规划方法

郭惠功，曲 龙，庞佳蕙，商志刚，*，周 锋

（1. 哈尔滨工程大学 水声技术全国重点实验室，黑龙江 哈尔滨 150001；2. 海洋信息获取与安全工信部重点实验室（哈尔滨工程大学）工业和信息化部，黑龙江 哈尔滨 150001；3. 哈尔滨工程大学 水声工程学院，黑龙江 哈尔滨 150001；4. 中国船舶集团有限公司第七〇三研究所，黑龙江 哈尔滨 150001）

0 引言

根据水声定位所依据信息的不同，现有的水声无源定位方法可以分为2 类。第1 类是基于信号到达方向（Direction of Arrival，DOA）的定位方法，第2 类是基于信号到达时间（Time of Arrival，TOA）的定位方法，TOA 定位方法要求接收机和发射机精确的时间同步；若信号收发机时间不同步，此时可使用基于信号到达时间差（Time Difference of Arrival，TDOA）的定位方法，基站间需要进行精确的时间同步。根据观测站数量的不同，无源定位可分为单站无源定位和多站无源定位[1]。在单站无源定位和多站无源定位中，基站的位置分布极大地影响了定位精度[2]。因此，如何规划机动观测平台的路径，实现定位节点的合理分布，对于提高目标定位精度至关重要。

无源定位中常用的衡量定位精度的指标有圆概率误差[3]、费歇尔信息矩阵（Fisher Information matrix，FIM）[4]、克拉美罗下界（Cramer-Rao Lower Bound，CRLB）和几何精度因子（Geometric Dilution of Precision，GDOP）等。众多研究采用以上指标对观测平台的轨迹进行了优化，文献[5]采用最小化广义克拉美罗下界的迹为优化准则对AOA 协同定位下多无人机的路径规划进行优化；文献[6]采用FIM 行列式的最大值作为目标函数，优化了TDOA 定位无人机群的轨迹；文献[7]采用最小化GDOP 为准则，优化了单测向观测器的运动轨迹；上述研究均通过选取合适的指标和优化准则，对观测器的轨迹进行了优化并提高了定位精度。

然而，在针对如何提升定位精度，优化观测器轨迹的同时，也应考虑来自障碍物或其他威胁等约束条件的影响。路径规划算法具有在复杂环境中为观测器规划出一条高效避障且威胁小的最优路径或次优路径的优点，常见的路径规划算法有：人工势场法[8]、动态窗口法（Dynamic Window Approach，DWA）[9]、A*算法、蚁群算法、遗传算法[10]和粒子群算法[11]等。路径规划算法之间不仅可以相互融合，而且还能与实际的任务场景相结合。文献[12]考虑了UAV 导航和双基地合成孔径雷达图像分辨率2 方面问题，提出了一种基于约束自适应多目标差分进化的路径规划算法。路径规划算法中DWA 算法不仅实现相对简单，而且可以通过改变采样策略、评价函数以及权重系数对算法进行调整和扩展，以适应不同的应用场景；文献[13]将障碍物数量因子与方向角变化因子引入评价函数，提高了机器人障碍物效果的同时保障了安全性；文献[14]提出了基于障碍物信息的速度权重动态调整机制，增强了无人机穿越密集障碍区域能力。

本文首先介绍了单观测平台基于TDOA 定位方法定位水下目标的基本原理；分析了不同航迹下的定位精度；针对定位精度受航迹影响的问题，提出了一种基于改进DWA 算法的航路规划方法。引入了以HDOP 最小化为准则构造的定位精度评价子函数，并使定位精度和航向角评价函数的权重系数可动态调整；以期规划出无碰撞且定位精度较高的航路。

1 定位态势

水下静止目标的定位态势如图1 所示。坐标系满足右手定则，X轴、Y轴和Z轴分别指向正东、正北和垂直向上；被定位目标位于海底，坐标为；单艘观测船按规划航迹在海面上航行，接收由声信标发射的周期声信号。设被定位目标的声脉冲的初始发射时刻为t0，周期为ts，则信号的到达时间可以表示为

图1 定位态势Fig. 1 Localization situation

式中：n为周期号；tn为第n个周期声信号的到达时间；dn为tn时刻观测船到目标的距离，为tn时刻观测船的坐标，由GPS 测得；c为水中声速。

2 TDOA 定位方法与精度分析

2.1 TDOA 定位方法基本原理

观测船对目标的TDOA 观测方程可写为

如图2 所示，观测船在定位过程中，会接收若干个周期声信号，因此在已驶航路上会存在若干个定位节点，引入N× 1矩阵（集合Γ包含N个可用的定位节点）

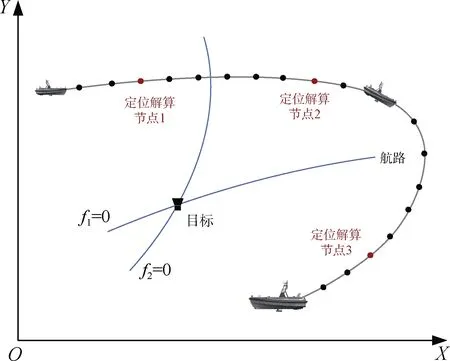
图2 单机动平台TDOA 定位示意图Fig. 2 Diagram of single motive station using TDOA localization

此时，基于TDOA 定位方法的数学模型写为

基于TDOA 的定位问题实际上就是对式（3）方程组的求解问题。如图2 所示，不利用冗余定位节点，至少需要在可用定位节点集合中选取出3 个定位解算节点，构成双曲线交汇模型才可以解算出目标的水平坐标[15]，此时对目标的定位转化为对以下方程组的求解

2.2 TDOA 定位精度分析

引入水平精度因子HDOP 作为评价定位精度的指标，HDOP 的值越小，定位精度越高[16]。HDOP的表达式为

式中：Δr=[Δxs, Δys]T表示定位解算结果与目标真实位置的偏差。

设Dx＝E( ΔrΔrT)为目标水平坐标测量误差的协方差矩阵，Dx的计算公式为

式中：Dc、Dt、Dz和DGPS分别是声速测量误差、到达时间测量误差、目标深度测量误差和观测船水平坐标测量误差的协方差矩阵；Mx、Mc、Mt、Mz和MGPS分别是F＝ [f1,f2]T关于变量 [xs,ys]、c、[t1,t2,t3]、zs和 [x1,y1,x2,y2,x3,y3]的雅可比矩阵。假设各测量误差均是相互独立且服从零均值高斯分布的随机变量，则上述协方差矩阵和雅可比矩阵的表达式为

式中：diag( •) 表示对角矩阵；σc、σt、σz、σGPS分别表示声速、信号到达时间、目标深度和观测船水平坐标测量的均方根误差。

对2 种航路下TDOA 法的定位精度进行分析，参数设置如下：声速为1 500 m/s；目标位于以原点为中心的400 m× 400 m 区域内，深度为50 m；σc、σt、σz和σGPS分别为1.5 m/s、1 ms、1 m 和2 m。2种航路下的定位精度分布情况如图3 所示，其中灰线为观测船的航路，红点为在航路上选取的定位解算节点，定位解算节点从两段距离相同的航路上被等长选取。由图3 可知，航路1 对目标区域的平均定位精度（3.16 m）比航路2 的平均定位精度（6.95 m）高；但是航路1 的盲区（黄色区域所示）比航路2要大。根据2 条航路下定位精度分布的特点，航路1和航路2 分别对应已经确定目标大致区域后的精确定位阶段和未确定目标大致区域时的粗略定位阶段。定位节点包围目标并呈等角分布是TDOA 定位的最优定位节点分布形式[17]。如图3（a）所示，航路1 的圆形航路下，更容易选取包围目标且接近等角分布的定位节点。因此，在精确定位阶段，观测船应尽可能地航行在环绕目标的圆形航路下。

图3 TDOA 法的定位精度分布Fig. 3 Localization precision distribution for TDOA algorithm

由定位精度分析可知，定位精度不仅受测量误差的影响，而且与定位节点的位置分布密切相关。由图2 可知，观测船的航路在很大程度上影响了定位节点的分布。因此，为提升定位精度，有必要对观测船的航路进行规划。

3 航路规划方法

3.1 传统DWA 算法原理

DWA 算法包含了3 部分：1）根据自身动力学性能和环境障碍物的限制生成动态窗口并进行速度采样；2）基于运动学模型和采样的速度进行轨迹预测；3）根据评价函数对预测轨迹进行评估。

观测船在水面上执行定位任务时，速度采样空间所受的限制如下。

1）观测船最小最大航速、转向速度限制。

式中：vmin和vmax为观测船的最小航行速度和最大航行速度；ωmin和ωmax为观测船的最小转向速度和最大转向速度。

2）观测船最小最大航行加速度、转向加速度限制。

式中：va和ωa分别为观测船当前航行速度和转向速度；和分别是观测船的最大航行加速度和最大转向加速度。

3）环境障碍物限制。

式中：distance(v,ω)为预测航迹到最近障碍物的距离，保证了当前速度下观测船可在碰到障碍物前停止。

动态窗口的速度采样空间Vr即为上述3 个集合的交集，满足

在每个离散时间间隔Δt内，对观测船的运动轨迹做近似化处理，看作是直线；则观测船的运动学模型可写为

式中：xk，yk和θk分别为观测船k时刻的X轴坐标、Y轴坐标和航向角；vk和ωk为观测船k时刻的航行速度大小和转向速度。

DWA 算法在速度采样空间Vr中离散化地选择可行的航行速度和转向速度，基于观测船的运动学模型，就可向前预测出一段时间T后的航迹。航迹的预测如图4 所示，绿色实线表示预测航迹。

图4 航迹预测图Fig. 4 Trajectory prediction diagram

对于每一条预测航迹，通过评价函数来评估其优劣程度。最终，将最优预测航迹对应的航行速度和转向速度作为控制量，控制观测船航行并执行任务。传统DWA 算法的评价函数为

式中： heading(v,ω)为航向角评价函数，heading(v,ω) ＝π -θ，θ为观测船在预测航迹末端时的航向和期望航向之间的角度偏差，期望航向为由预测航迹末端指向目标点的方向； dist(v,ω)为避障评价函数， dist(v,ω) ＝distance(v,ω)，评估预测航迹到最近障碍物的距离，当观测船与障碍物之间的距离超过一定值时，设置为常数；velocity(v,ω)为速度评价函数， velocity(v,ω) ＝v，评估预测航迹对应的速度大小；α、β、γ分别为各评价子函数的权重系数；σ表示对各评价子函数进行归一化。

3.2 改进DWA 算法

传统DWA 算法只考虑了如何在躲避障碍物的同时快速地抵达目标，并未考虑定位精度问题。因此，本文在传统DWA 算法的评价函数的基础上，引入定位精度评价子函数，以提升对目标的定位精度。

如图5 所示，通常情况下，从历史航迹中选取1号定位解算节点和2 号定位解算节点，当前时刻选取为3 号定位解算节点，通过式(1)对目标进行实时定位解算，设1 号和2 号定位解算节点的坐标分别为Xh,1和Xh,2。由式(11)向前预测某条航迹的同时，可根据声信号发射周期ts，推算出观测船在该条预测航迹上接收到未来M个声信号的大致位置（M×ts≤T），并将此M个点作为预测定位解算节点（如图5 中红色圆点所示），设该条预测航迹上第j个预测定位解算节点的坐标为Xp,j，j∊ [1,M]，则该条预测航迹上的预测定位解算节点坐标集为{Xp,1,Xp,2,…,Xp,M}。

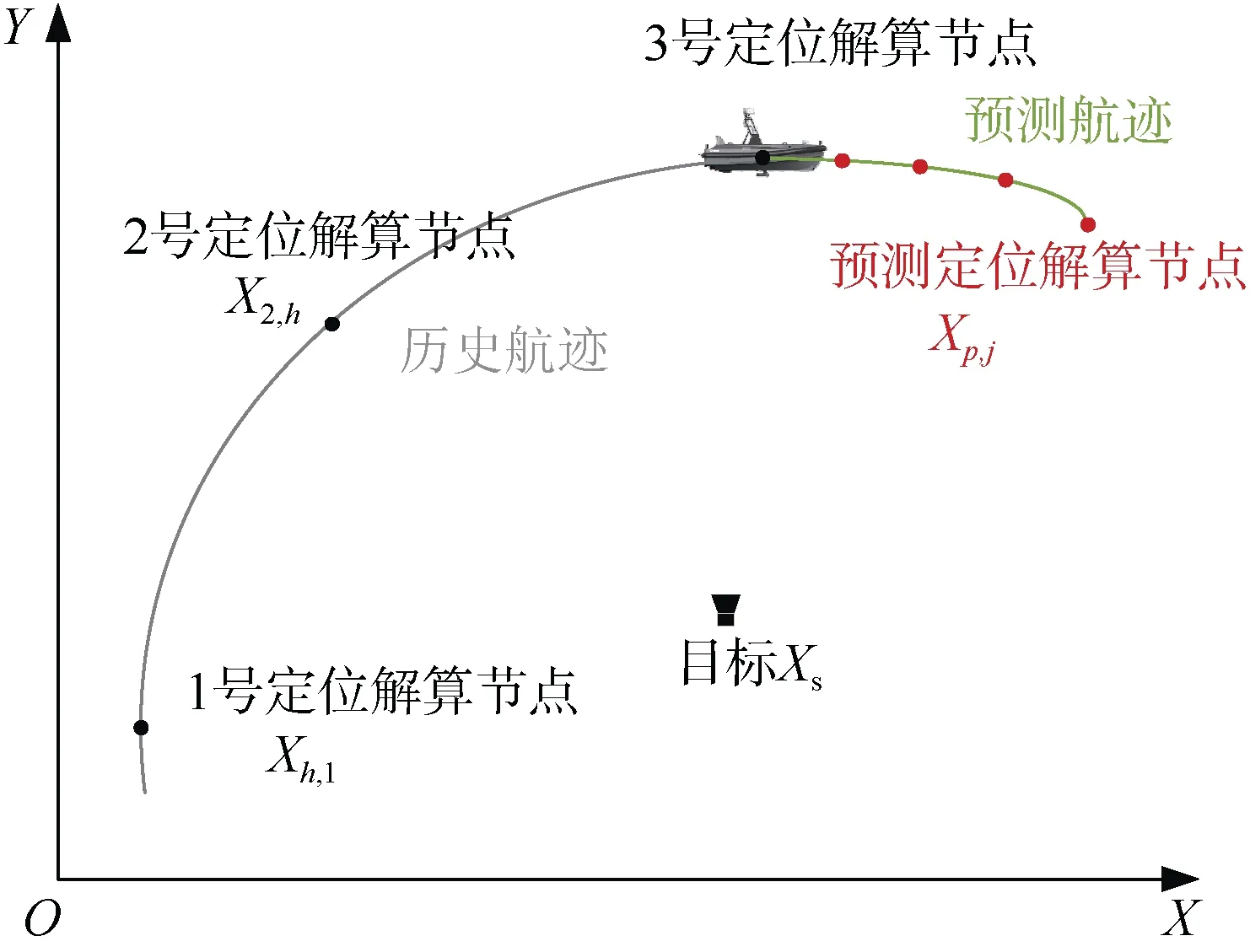
图5 定位节点的选取示意图Fig. 5 Diagram of localization nodes selection

本文以HDOP 最小化为优化准则，对预测航迹进行针对定位精度的评价。由HDOP 的计算式可知，在测量误差已知或已假设的条件下，HDOP 是只与目标和3 个定位解算节点的坐标有关的函数，但是在定位问题中目标的真实坐标Xs始终未知，因此计算HDOP 时，由定位解算结果替代。HDOP 值越大，定位精度越低，定位精度评价函数值与HDOP值呈负相关。因此，定义该条预测航迹的定位精度评价函数为

整个过程采用边定位目标边规划航路的策略，在定位初期阶段，观测船距离目标位置较远，定位误差较大，定位解算结果不准确， hdop(v,ω)的可靠性差，观测船应尽量快地抵达目标所在区域。随着观测船与目标间距离的减小，信噪比增大，时延估计标准差σt反比于信噪比[18]，声呐对信号到达时间tn的测量精度提高，定位结果逐渐趋于真值Xs，计算出的hdop(v,ω)逐渐可靠。因此，在观测船靠近目标的定位过程中，随着观测船与目标距离的减小，定位精度评价函数的权重应该逐渐增加，航向角评价函数的权重逐渐降低。

如图6 所示，考虑到水下定位所使用的声呐垂直开角范围有限[19]，为避免观测船过于靠近目标，导致目标进入盲区而丢失信号，需设计一个最小水平距离rm。综上所述，改进后的评价函数为

图6 声呐垂直开角示意图Fig. 6 Vertical directivity of sonar

式中：λ为定位精度评价函数的权重系数；p为观测船到目标位置的水平距离。

由式（15）可知，在远距离情况下（p≫rm），ε的值较小，此时heading(v,ω)对评价函数的影响较大，观测船快速地向目标区域靠近。观测船在接近目标的过程中，ε的值趋于1，此时heading(v,ω)对评价函数的影响降低，hdop(v,ω)对评价函数的影响增大，航路的规划更多地取决于hdop(v,ω)。

4 仿真验证

通过仿真实验对本文所提算法的有效性进行验证。水下目标的水平坐标设为[–400，–400] m，深度为70 m，发射周期为1 s；声速为1500 m/s；最小水平距离rm为180 m；观测船起点为[–700，800] m；环境中设置8 个障碍物，其位置坐标分别为[–200，0] m，[–200，200] m，[–200，–300] m，[170，–200] m，[70，–200] m，[–400，–700] m，[100，100] m，[200，200] m，半径分别为30 m，20 m，30 m，30 m，20 m，20 m，30 m，40 m；测量误差的参数设置同定位精度分析时一致，仿真参数见表1，其中动力学性能参数参考自文献[20]。本文进行了3 种航路下的仿真实验，分别是航路1：常规匀速直线航路；航路2：基于传统DWA 算法规划出的直达目标区域的航路；航路3：基于改进DWA 算法规划出的航路。

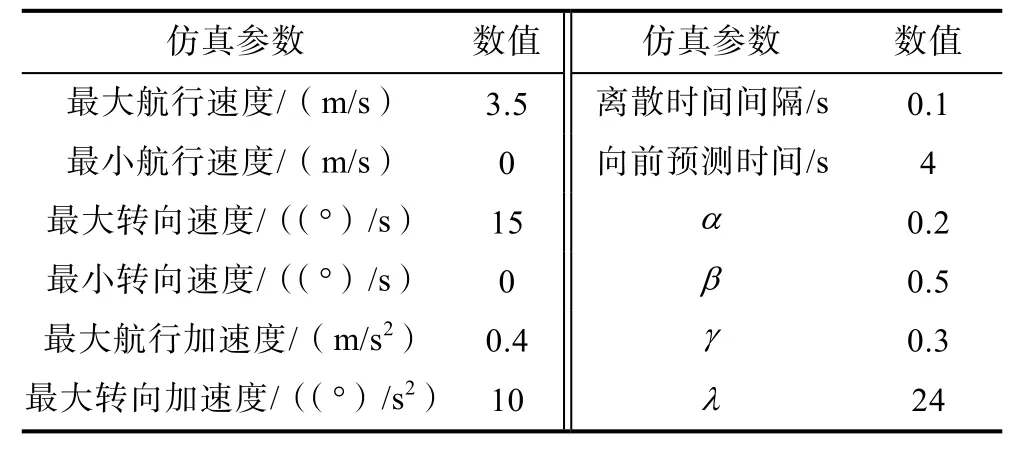
表1 仿真参数Table 1 Parameters

1）航路1。

规划的航路如图7（a）所示，其中蓝色为规划的航路，黑色为障碍物，红色星号为目标，蓝色圆点为所选取的3 个定位节点。为简化处理，仿真中所用的节点选取策略为：当前位置为3 号定位节点，并往前每隔100 个周期号选取一个定位节点；定位结果如图7（b）所示；整个定位过程中定位误差如图7（c）所示。此常规匀速直线航路为基于传统DWA算法向预设终点引导而规划出的，预设终点的位置为[800，–100] m。

图7 航路1 的仿真结果Fig. 7 Simulation results of Path 1

2）航路2 和航路3。

图8（a）和图8（d）中前一段蓝色航路与图7（a）中一致，同为基于传统DWA 算法向预设终点引导而规划出的直线航路。此段蓝色航路期间TDOA 定位的基线长度随着船的航行而不断增长，定位精度随基线的增长而提升，待基线增长至一定长度，定位解算结果较可靠之后，可得出目标所在大致区域，然后再基于传统DWA 算法和改进DWA算法规划航路（如图8（a）和图8（d）中红色航路所示）。

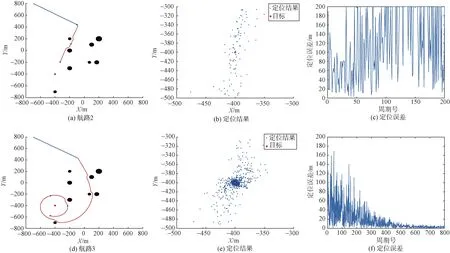
图8 航路2 和航路3 的仿真结果Fig. 8 Simulation results of Path 2 and Path 3

由图8（c）可知，当观测船直接向目标抵近时，定位误差很大，甚至无法进行定位解算。这是因为TDOA 定位方法在基线方向上的定位精度很低，尤其当目标处于定位节点包围区域外并和3 个定位节点的任何2 个趋于共线时，定位精度变得极差，无法对声源进行有效定位。因此，当使用单观测平台基于TDOA 定位方法对目标进行定位时，不能使观测船直接向目标所在区域抵近。对比图7 和图8 可以看出，改进DWA 算法规划航路下的定位结果更接近于目标真实位置，定位误差更小，并且观测船在抵达最小水平距离rm后，在定位精度评价函数的作用下自动选择了定位精度更高的圆形航路绕目标航行。传统DWA 算法规划的航路1 在整个定位过程中定位精度稳定，均方根误差为55.9 m；改进DWA 算法规划的航路 3 在整个定位过程中的均方根误差为31.2 m，后半段的均方根误差为5.3 m；航路2 因其无法有效定位，故不讨论其误差。因此，改进DWA算法规划的航路不仅有效避开了障碍物，而且由于定位精度评价函数的引入，航路对应的定位精度得以提高。

5 结束语

针对单艘观测船TDOA 定位水底静止目标的问题，本文提出了一种基于改进DWA 算法的航路规划方法。首先，结合DWA 算法向前预测的特点，设计了一种定位精度评价子函数，提升了定位精度。其次，根据观测船与目标的距离关系，平衡了航向角评价子函数和定位精度评价子函数的权重系数，使航路规划方法更加贴合定位任务。最后，通过仿真实验对比了传统DWA 算法和改进DWA算法，证明了基于改进DWA 算法所规划出的航路相比传统算法的定位精度有显著提高。