基于条件平差的变形监测控制网数据处理及分析

曹元志 黄长军

摘要：在某几何模型中，总的实际观测次数为n，必要观测次数t，则多余观测次数r=n－t，那么可列立r=n－t个独立条件方程，这种以条件方程为函数模型的平差方法，称为条件平差法。在变形监测控制网数据处理中，通常可以采用条件平差法对网中的观测数据进行平差和点位精度分析，求出最弱点中误差、最弱边中误差、绘制误差椭圆。其中处理的关键是条件方程式的列立、非线性条件方程式线性化、误差方程式的求解及未知点精度评定。本文以在益阳市资江三桥布设的桥梁控制网为例，推导了全部的桥梁控制网解算过程，并得出了结论。

关键词：条件平差；法方程；測量平差；线性方程组

DataProcessingandAnalysisofDeformationMonitoring

andControlNetworkBasedonConditionAdjustment

CaoYuanzhiHuangChangjun

HunanCityUniversityInstituteofMunicipalandMappingEngineeringHunanYiyang413000

Abstract：Inacertaingeometricmodel，thetotalactualnumberofobservationsisn，andthenecessarynumberofobservationsist，sothenumberofobservationsrisredundant.Thenanindependentconditionalequationr=ntcanbelisted.Thisadjustmentmethodbasedonconditionalequationasafunctionmodeliscalledconditionaladjustmentmethod.Inthedataprocessingofdeformationmonitoringandcontrolnetwork，itisusuallypossibletousetheconditionadjustmentmethodtoanalyzetheadjustmentandpointpositionaccuracyoftheobserveddatainthenetwork，tofindouttheerroroftheweakestpoint，theerroroftheweakestedge，anddrawtheerrorellipse.Thekeytodealwiththeseproblemsaretheformulationofconditionalequations，linearizationofnonlinearconditionalequations，solvingoferrorequationsandevaluatingtheaccuracyofunknownpoints.TakingthebridgecontrolnetworkinZijiangBridgeNo.3ofYiyangCityasanexample，thispaperdeducesalltheprocessofsolvingthebridgecontrolnetworkanddrawsaconclusion.

Keywords：Adjustmentofconditions；Normalequation；Adjustmentofmeasurement；Systemoflinearequations

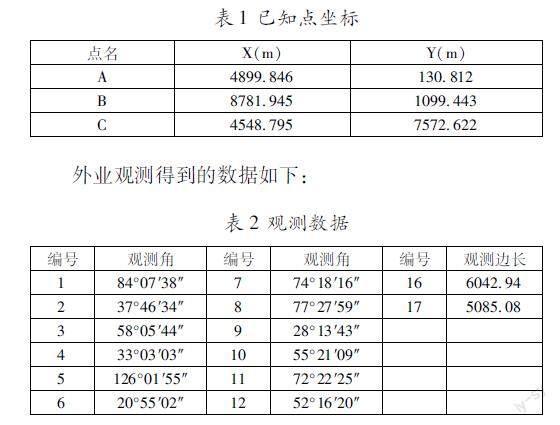
在现代桥梁控制网布设中，通常布设成GPS网或边角网［1］。布设为GPS网的优点是不受地形和通视条件的限制，布设为边角网的优点是既观测角度又观测距离，精度相对较高［2］。本课题结合边角网的布设优点对益阳市资江三桥进行控制测量。2021年以来，益阳市资江三桥由于车流量较大，投入使用时间较长，在运营过程中出现了桥墩倾斜下沉、桥面平整度发生变化的情况。为了了解资江三桥的真实变形速率及沉降规律，笔者布置了一测角测距的边角控制网。所用仪器为徕卡TC702型全站仪，测角中误差为±2″，测距精度为1mm+2ppm×D（公里）。如图1所示，A，B，C是已知点，P1，P2为待定点，网中观测了12个角度，2条边长（在条件平差中，不用观测边长；在间接平差中，用16，17作为观测边长），观测4个测回。控制网图见图1。

图1控制网图

已知点的坐标数据如下：

1条件平差解算

1.1条件方程的列立

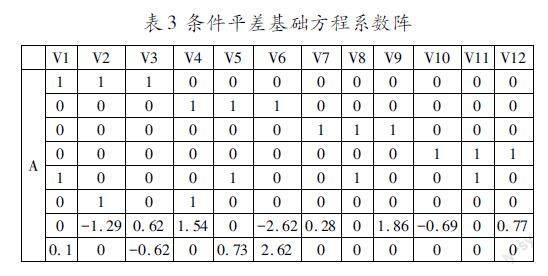
观测值n=12，必要观测t=4，多余观测r=8，可知要列8个条件方程，如下：

图形条件：

V1+V2+V3+W1=0V4+V5+V6+W2=0

V7+V8+V9+W3=0V10+V11+V12+W4=0

圆周条件：

V1+V5+V8+V11+W5=0

已知方位角条件：

V2+V4+W6=0

极条件（已线性化）：

cotL12V12+cotL5V5+cotL9V9-cotL10V10-cotL6V6-cotL2V2-cotL7V7+ρ×1-sinL2sinL6sinL7sinL10sinL3sinL5sinL9sinL12=0

已知边条件：

cotL1V1+cotL6V6-cotL3V3-cotL5V5+ρ×1-sinL3sinL5sinL1sinL6=0

其中：

W1=L1+L2+L3-180°W2=L4+L5+L6-180°

W3=L7+L8+L9-180°W4=L10+L11+L12-180°

W5=L1+L8+L11+L5-360°W6=L2+L4-（BA-BC）

代入数据，得：

V1+V2+V3-2.8=0V4+V5+V6+1.2=0

V7+V8+V9-0.9=0V10+V11+V12-3.8=0

V1+V5+V8+V11-1.2=0V2+V4+1.1=0

0.1V1-0.62V3+0.73V5+2.62V6-1.92=0

-1.29V2+0.62V3+1.54V4-2.62V6-0.28V7+1.86V9-0.69V10+0.77V12=0

得到基礎方程系数阵：

Naa300011-0.6-0.5030011-1.13.30030102.100003100.1011114000.81100020.20-0.7-1.12.10.0800.215.8-7.2-0.53.4000.80-7.27.7

由法方程式可以解出：

2条件平差精度评定

未知点坐标的函数关系式为：

XP1=cos（AB+L＾3）+XAYP1=sin（AB+L＾3）+YA

XP2=cos（360°-P2P1+L＾9）+XAYP2=sin（360°-P2P1+L＾9）+YA

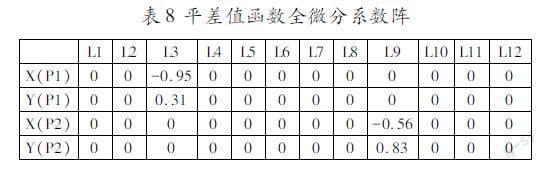
对其进行全微分，得其系数阵：

表8平差值函数全微分系数阵

L1L2L3L4L5L6L7L8L9L10L11L12X（P1）00-0.95000000000Y（P1）000.31000000000X（P2）00000000-0.56000Y（P2）000000000.83000

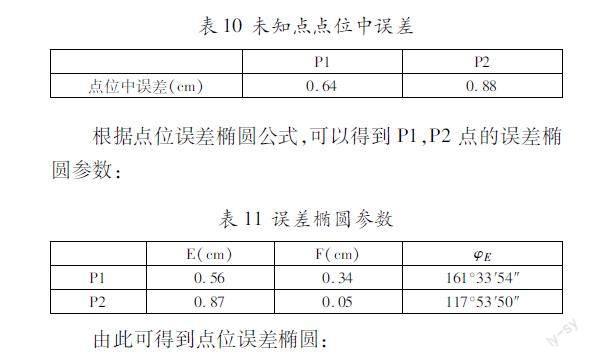
按照协因数传播律，未知点坐标的协因数为：

Qσ＾σ＾=fTQf-（AQf）TN-1aaAQf

得平差值函数的协因数阵：

根据点位误差椭圆公式，可以得到P1，P2点的误差椭圆参数：

结语

通过条件平差条件对益阳市紫江三桥控制网进行数据处理和精度评定，可以看出条件平差和间接平差的不同点。条件平差和间接平差都是具有无穷多组解的相容方程组［7］。条件平差与间接平差都是在最小二乘准则的约束下求得最优解［8］。对于同一平差问题，无论采用何种平差方法，所得到的平差结果和精度（包括点位中误差，点位误差椭圆）都是相同的。条件平差与间接平差是整个测量平差的基础，其他诸多平差方法都是在这两种平差方法的基础上发展起来的。对于任一问题，既可采用条件平差又可采用间接平差进行计算，不同平差方法所产生的条件系数阵A与间接平差系数阵B的积为0，即A*B=0。

参考文献：

［1］张正禄.工程测量学的研究发展方向［J］.现代测绘，2003（03）：36.

［2］王晓光，谢振红.导线间接平差法［J］.吉林建筑工程学院学报，2007（01）：5862.

［3］张后苏.条件平差与间接平差间的转换［J］.有色金属（矿山部分），1988（04）.

［4］武汉大学测绘学院测量平差学科组.误差理论与测量平差基础［M］.出版地：武汉大学出版社，2003.

［5］王新洲.论经典测量平差模型的内在联系［J］.测绘通报，2004（02）：14.

［6］周世健，臧德彦，鲁铁定.测量平差中各种模型的等价转换关系［J］.测绘学院学报，2001（01）：13+7.

［7］袁泽喜.导线平差方法的应用与分析［J］.西部探矿工程，2005（09）.

［8］梁永成，曲建光.相对点位中误差及其在工程测量中的作用［J］.测绘工程，1995（04）：4854.

基金项目：湖南省自然科学基金联合基金项目（2022JJ50261）；湖南省自然科学基金面上项目（2021JJ30076）

作者简介：曹元志（1977—），男，汉族，河南信阳人，硕士，副教授，注册测绘师，主要从事工程测量及数据处理的教学和科研。