关于两个线性方程组同解条件的再思考
2014-09-17陈耀光
陈耀光
(新疆大学数学与系统科学学院,新疆乌鲁木齐830046)
线性方程组是大学本科中工科线性代数的最重要也是最主要的部分,它贯穿于线性代数的始终,也可以说线性代数就是线性方程组的代数,因此在线性代数中对线性方程组的讨论已经比较充分,但在教学过程中,学生经常会问到两个线性方程组的解与解有什么关系?如何判断?如何求解?关于这一点工科线性代数中几乎没有讨论,在其它教材中也讨论甚少,即使有也不全面.而在文献[1]中,虽然对此进行了讨论,但所给结论的条件出现了漏洞.为此笔者通过查阅大量相关资料,并进行深入分析与研究,得到了本文相关结论及方法.
1 预备知识
设非齐次线性方程组
Ax=b,
(1)
其中

非齐次线性方程组的向量形式
x1t1+x2t2+…+xntn=b.
(2)

引理2非齐次线性方程组(1)有解的充分必要条件是向量b可由向量组t1,t2,…,tn线性表示.
2 两个方程组的解与解的关系
设有两个非齐次线性方程组
Ax=c
(3)
及
Bx=d,
(4)
其中

其所对应的齐次方程组
Ax=0
(5)
及
Bx=0
(6)
定义如果有n维向量x同时满足非齐次线性方程组(3)和(4),则称向量x为非齐次方程组(3)和(4)的公共解.如果方程组(3)的任意解都是方程组(4)的解,而方程组(4)的任意解都是方程组(3)的解,则称方程组(3)和方程组(4)是同解的.
对于齐次方程组(5)和(6)也同样有非零公共解和非零同解的概念,这里就不再赘述了.
3 两个非齐次方程组有公共解的充分必要条件
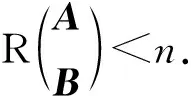

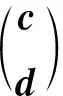
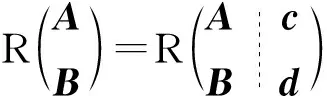
反之,非齐次线性方程组(3)和(4)都有解,非齐次线性方程组(3)和(4)不一定有公共解.
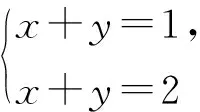
4 两个线性方程组同解的充分必要条件
1.两个齐次线性方程组同解的充分必要条件.
引理6齐次线性方程组Ax=0与Bx=0同解的充分必要条件是

引理7齐次线性方程组Ax=0与Bx=0同解的充分必要条件是A的行向量组与B的行向量组等价.
定理1齐次线性方程组Ax=0与Bx=0有非零同解的充分必要条件是

2.两个非齐次线性方程组同解的充分必要条件.
在上面我们研究了两个线性方程组有公共解的问题.很明显,如果两个线性方程组同解,则这两个线性方程组一定有公共解.反之,当两个线性方程组有公共解时,这两个线性方程组不一定同解.而对于两个线性方程组同解的条件,文献[1]中对此进行了相应的讨论,并给出了如下两个结论(文献 [1]中的定理2):

结论2设非齐次线性方程组(3)和(4)都有解,则非齐次线性方程组(3)和(4)同解的充分必要条件是所对应的齐次线性方程组(5)和(6)同解.
对于结论2,通过研究和讨论,其必要性是完全正确的,但其充分性是有问题的.对此,笔者从理论和实例两个方面来加以说明.
首先设向量组a1,a2,…,am是齐次线性方程组(5)的系数矩阵A的行向量组,向量组b1,b2,…,bs是齐次线性方程组(6)的系数矩阵B的行向量组.注意向量组a1,a2,…,am与α1,α2,…,αm的差异,向量组b1,b2,…,bs与β1,β2,…,βs的差异.
若齐次线性方程组Ax=0与Bx=0同解,由引理7知向量组a1,a2,…,am与向量组b1,b2,…,bs等价.而向量组a1,a2,…,am与向量组b1,b2,…,bs等价推不出向量组α1,α2,…,αm与向量组β1,β2,…,βs等价(如(1,2,-1)与(2,4,-2)等价,但(1,2,-1,1)与(2,4,-2,3)不等价),从而推不出非齐次线性方程组(3)和(4)同解.
再则也可以看一反例:方程组
x+y=1
有解, 方程组
x+y=2

定理2设非齐次线性方程组(3)和(4)都有解,则方程组(3)和(4)同解的充分必要条件是所对应的齐次线性方程组(5)和(6)同解,且非齐次线性方程组(3)和(4)至少有一个公共解.
证必要性参见文献[1].
充分性.设RA=r.由已知非齐次线性方程组(3)和(4)所对应的齐次线性方程组(5)和(6)同解,所以RA=RB=r,并且Ax=0的基础解系ξ1,ξ2,…,ξn-r也是方程组Bx=0的基础解系.又因为Ax=c及Bx=d有解且至少有一个公共解,不妨设为η*,则
x=k1ξ1+k2ξ2+…+kn-rξn-r+η*
既是Ax=c的通解,也是Bx=d的通解,所以方程组(3)和(4)同解.
定理3设非齐次线性方程组(3)和(4)都有解,则方程组(3)和(4)同解的充分必要条件是

此定理的证明可由引理4和引理6直接得到.
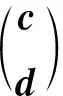
此定理的证明可由引理5和引理6直接得到.
5 两个方程组同解的判断及同解的求法
以下我们仅对非齐次线性方程组加以讨论,而对于齐次线性方程组其方法类似.
设有两个非齐次线性方程组
Ax=c
(3)
及
Bx=d.
(4)
如果能判断出(3)和(4)同解,则它们的同解的求法就很简单了,只要求出(3)或(4)的通解就行了.而同解的判断可以根据定理3的结论来加以进行.下面就通过具体实例来说明这一方法.
例1设非齐次线性方程组

讨论这两个方程组是否有公共解,是否同解?如同解,则求其同解的通解形式.
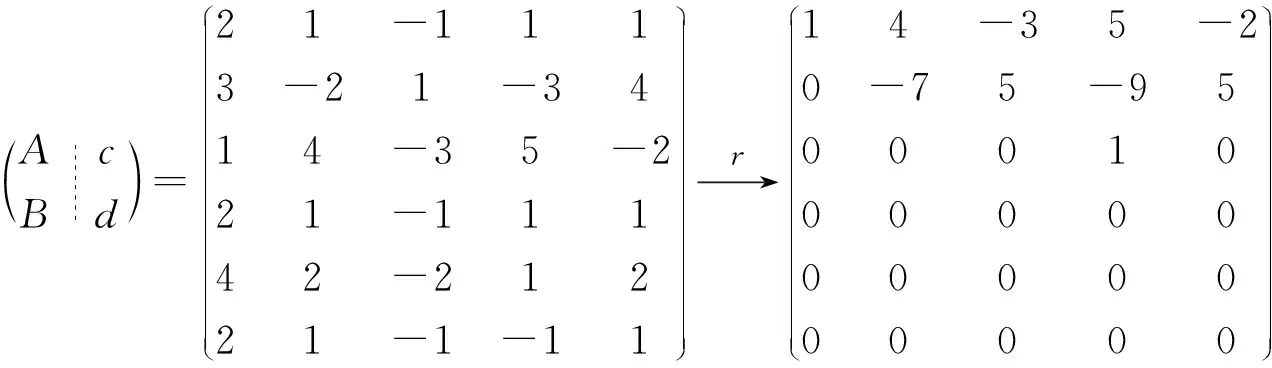
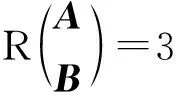
即已知的两个方程组所对应的齐次方程组不同解,所以已知的两个方程组不同解.
本例说明,在定理2的充分条件中两个非齐次线性方程组所对应的齐次线性方程组(5)和(6)同解的条件不可缺少,而在第四部分中的反例说明在定理2的充分条件中两个非齐次方程组(3)和(4)至少有一个公共解的条件不可缺少.
例2设非齐次方程组

讨论这两个方程组是否有公共解,是否同解?如同解,则求其同解的通解形式.
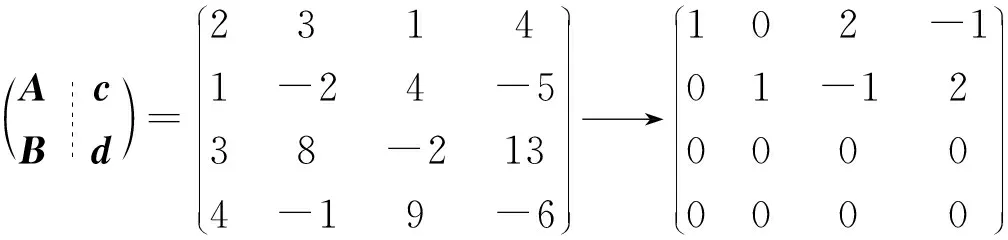
易知RB=2. 所以

由定理2知,已知的两个线性方程组同解,且同解的通解形式为
[1] 罗家贵. 关于线性方程组同解的条件[J].大学数学,2012,28 (3):141—145.
[2] 尹晓东. 线性代数习题课需要解决的几个问题[J].大学数学,2012,28 (2):139—141.
[3] 同济大学. 线性代数 [M].5版.北京:高等教育出版社,2007.
