考虑90°子铺层的T300/69层合板断裂韧性数值模拟和实验研究
2024-01-06韦尧兵王雪雪靳翌帆刘俭辉郎珊珊
韦尧兵, 王雪雪, 靳翌帆, 刘俭辉, 郎珊珊
(1. 兰州理工大学 机电工程学院, 甘肃 兰州 730050; 2. 西安咸阳国际机场股份有限公司, 陕西 西安 710000)
与传统单相材料(金属、陶瓷和聚合物)相比,复合材料具有比强度大、比刚度高、抗疲劳性能好、质量轻和可设计性强等诸多优点,被广泛应用于各个行业中,最新军用或民用飞机的大部分部件都是由复合材料制成的[1-3].复合材料的性能通常取决于其增强材料的类型和性能,通过基体和增强体的适当组合,可以获得不同加载条件下复合材料所需的力学性能.
复合材料层合板初始裂纹的出现和扩展比较复杂.传统复合材料层合板大多为对称铺设,即将层合板结构设计成均衡对称形式.在层合板铺层数量较少时,90°子铺层对断裂韧性的影响可以忽略不计.随着层合板铺层厚度增加,90°子铺层会对复合材料层合板整体断裂韧性产生一定影响,且随着裂纹张开位移的不断增大,纤维与基体出现脱粘现象,桥联纤维会出现损伤,最终导致纤维断裂.传统的扩展有限元模型在模拟裂纹方面有很大的优势[4],可以考虑每个子铺层对层合板整体性能的影响,但不能模拟桥联现象.因此,建立考虑90°子铺层和纤维脱粘对碳-环氧复合材料层合板断裂韧性影响的计算方法具有重要意义.
目前,用于预测单向纤维增强的层压复合材料损伤模型已经成熟,但在强度预测方面仍需进一步研究.实验证明,相比无损复合材料,含缺口的复合材料强度下降明显,Waddoups等[5]提出了修正的应力强度因子准则,认为孔边损伤区达到一定尺寸且层合板达到断裂韧性KIC时才会发生破坏.Whitney等[6]针对缺口复合材料层合板提出了点应力模型和平均应力模型.点应力模型的基本理论是,当层合板在距孔边指定点处的应力达到层合板无缺口强度时将发生破坏;而平均应力模型的基本理论是,当层合板在距孔边指定距离内的平均应力达到层合板无缺口强度时将发生破坏,该指定距离被称为特征长度,只与铺层方式和铺层角度有关.但是,储辰辰等[7]和刘岩松等[8]发现,这些特征长度并非常数,与材料、铺层、板宽和孔径大小都有关,提出的各种修正准则中需要大量开孔板强度拟合有关参数.孙国芹等[9]和王昊元等[10]针对临界距离法和权函数的限制条件,通过开孔等效法并结合无损伤层合板疲劳寿命模型,建立了含冲击损伤的复合材料层合板疲劳寿命预测模型,可是实验数据有限.杨江波等[11]提出了线弹性断裂力学解法(linear elastic fracture mechanics,LEFM),与固有缺陷模型相似,区别在于可由一次独立的断裂韧性实验计算出不同的特征长度,不再依赖多个开孔板强度的拟合,可节省大量实验耗费.Aoki等[12]探讨了层合板厚度和0层比率对薄层复合材料强度和破坏行为的影响.但是,目前关于复合材料铺层厚度、特殊铺层角度和基体强度较高等情况对层合板强度影响的研究较少.
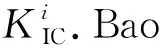
首先,本文利用ABAQUS有限元软件中扩展有限元法(extended finite element method,XFEM)进行裂纹扩展模拟,得出模拟的断裂韧性;并通过虚拟裂纹闭合技术(virtual crack closure technology,VCCT)计算归一化能量释放率,为后续处理实验数据提供理论依据.其次,通过紧凑拉伸实验研究不同铺层方式下T300/69复合材料层合板的断裂韧性,利用载荷-位移数据计算不同铺层方式下复合材料层合板的断裂韧性.随后,借助扫描电镜(SEM)观察断口形貌,研究90°子铺层和纤维脱粘现象对复合材料层合板整体断裂韧性的影响.最后,基于多向层压板的断裂韧性计算方法,考虑不同铺层方式下90°子铺层和纤维脱粘时所释放的能量,提出修正的多向层压板断裂韧性计算模型.
1 紧凑拉伸实验
1.1 实验参数
T300/69复合材料层合板CT试件单层厚度为0.15 mm,名义纤维含量Vf为0.65.按照要求完成[0/90]s、[0/90]2s、[0/90]4s、[0/±45/90]s、[0/±45/90]2s、[0/±45/90]4s这6种铺层方式的铺设,将板料放入热压机中抽真空,先在90 ℃和4 MPa的条件下保温保压30 min,再在120 ℃和10 MPa的条件下保温保压120 min.紧凑拉伸试样尺寸根据ASTM E399-90标准设计,如图1a所示;借助雕刻机按要求进行数控切割,加工完成后的试件如图1b所示.实验在湿度为35%的室温下进行,试件逐一编号,用游标卡尺测量试件初始裂纹长度a0、板厚度B、板宽度W,精确至0.1 mm,读数3次并取平均值.

图1 T300/69模型和试样
在SDS100电液伺服疲劳实验机进行T300/69复合材料层合板紧凑拉伸实验,并记录拉伸过程的位移-载荷曲线.实验结束后利用扫描电子显微镜观察层合板断口形貌.材料性能如表1所列.
1.2 位移-载荷曲线
根据实验数据拟合出不同铺层的位移-载荷曲线,如图2所示,为计算不同铺层方式的断裂韧性提供基础.结果表明,层合板的铺层角度和含90°子铺层的层合板铺层厚度均会影响层合板整体的断裂韧性.

表1 T300/69组分和单向复合材料性能
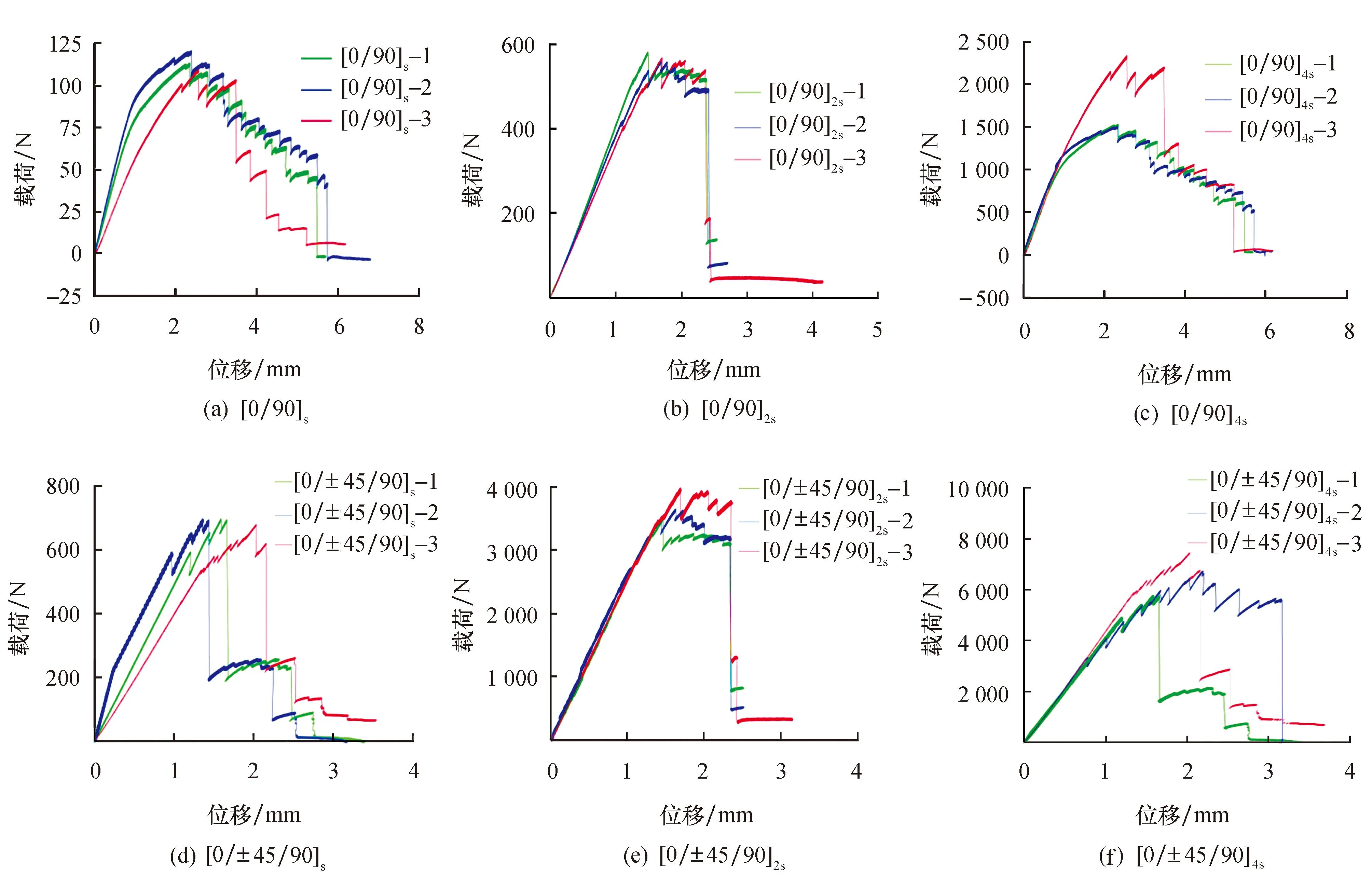
图2 载荷-位移曲线Fig.2 Load-displacement curve
由图2a可以看出,厚度较薄的层合板在拉伸过程中存在一定的失稳现象,而较厚的层合板在拉伸过程中失稳现象不严重.对比图2a~图2f可以看出,90°子铺层的增加对层合板整体断裂韧性存在一定的影响,层数的增加导致裂纹最大扩展载荷不断增加.
1.3 能量释放率
Shibanuma等[17]对纤维层压板CT试样进行有限元分析后提出了临界能量释放率公式,即
(1)
式中:Pmax为加载过程中裂纹扩展对应的载荷;f(a)为应变能释放率.
鉴于层合板尺寸的限制,取裂纹长度a=1.4 mm进行模拟,运行每个模型从而获得裂纹尖端周围的J积分.
利用式(1)计算得到紧凑拉伸实验结果,如表2所列.
由表2可以看出,T300/69复合材料层合板的断裂韧性与铺层方式存在联系.对比A1~A3、B1~B3、C1~C3与D1~D3、E1~E3、F1~F3可以看出,相同铺层方式下层数越多断裂韧性越高;对比B1~B3、D1~D3与C1~C3、E1~E3可以看出,相同厚度下不同铺设方式的层合板断裂韧性也不相同,采用更复杂铺层方式的层合板断裂韧性要高于正交层合板的断裂韧性.
表2 紧凑拉伸实验结果
2 含裂纹复合材料层合板有限元模拟
在ABAQUS软件中建立不同铺层方式的复合材料层合板模型,并对其进行数值仿真.采用扩展有限元法,获得中心长度为2a的贯穿裂纹和在远场受拉伸作用时复合材料层合板的裂纹尖端应变能释放率.利用虚拟裂纹闭合技术计算归一化的应变能释放率f(a),并将理论值与实验值进行对比,为计算紧凑拉伸试样的应变能释放率GIC做准备工作.
2.1 中心贯穿裂纹复合材料层合板有限元模拟
对不同铺层方式下中心长度为2a的贯穿裂纹复合材料层合板进行有限元计算,得到不同铺层方式下裂纹扩展应变能释放率.不同铺层方式GIC结果如表3所列,平均应变率为75%的扩展有限元结果如图3所示.

表3 不同铺层方式下层合板应变能释放率GIC
对比图3a~3c与图3d~3f的铺层方式可以看出,随着层合板的层数增加,层合板应变能释放率逐渐增高.对比图3b、3d与图3c、3e的模拟结果可以看出,铺层方式更复杂的层合板应变能释放率要高于相同层数正交层合板的应变能释放率.因此,铺层方式对中心贯穿裂纹复合材料层合板的断裂韧性确定存在一定影响.
2.2 应变能释放率的归一化处理
本文借助Shibanuma等[17]采用的有限元分析方法,得到更精确的应变能释放率,如表4所列.
该方法需要在稳定的裂纹扩展条件下应用.但在实验中,因夹具与试件间的摩擦以及试件自身的缺陷而导致真实的能量释放率仍包括其他损伤模式消耗的能量,与模拟的数值存在一定误差.

表4 T300/69层合板归一化应变能释放率
3 断裂韧性修正模型
3.1 多向层合板的断裂韧性
(2)
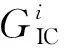
该模型的显著特点是,只利用铺层的弹性特性和0子层的断裂韧性便可预测一般纤维主导层合板的断裂韧性.
3.2 界面脱粘对断裂韧性的影响
复合材料基体和纤维界面的拉伸和剪切强度较低,界面上难免会有缺陷和微裂纹,这种现象对复合材料的细观和宏观性能都有很大影响.由于纤维拔出过程需要吸收能量,所以Kozar等[18]作出以下假设:纤维断口随机分布,纤维拔出过程中界面初始剪应力保持不变,并忽略基体的塑性流动.由实验所得T300/69复合材料纤维部分性能参数如表5所列.
由于式(2)未考虑界面脱粘对断裂韧性的影响,所以本文在式(2)的基础上借助界面脱粘对GT进行修正,即
(3)

表5 T300/69复合材料纤维部分性能
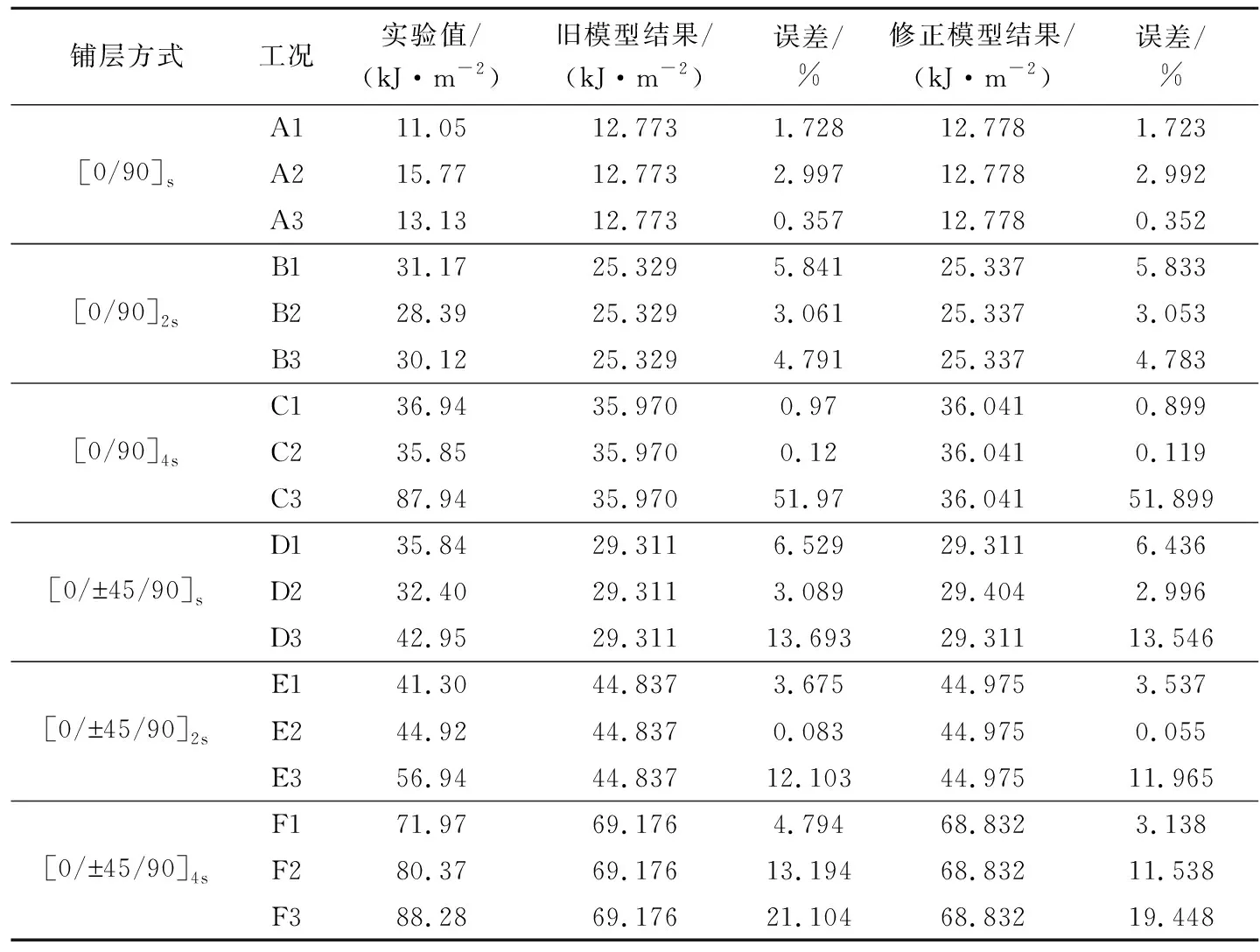
式中:GT为界面脱粘时的断裂韧性;由实验可得0 基于细观力学,层合板裂纹扩展时,由于90°子铺层断裂特殊的铺设角度被直接简化为基体断裂,纤维强度往往大于基体强度,断裂后基体中仍有部分纤维并未完全断裂,基体开裂后纤维被继续拉长,界面脱胶,所以90°子铺层的基体断裂不可忽视.综上所述,利用式(1)得到的计算结果存在一定误差,考虑90°子铺层的断裂韧性,结合式(1)和式(2)可得层合板整体的断裂韧性修正方程,即 (4) 式中:M为90°子铺层层数. 将有限元模拟值即多向层压板的断裂韧性值(旧模型)、考虑90°子铺层和纤维脱粘的断裂韧性值(修正模型)与实验值分别进行对比,所得误差如表6所列. 表6 断裂韧性值和误差结果 由表6可以看出,实验值与模拟值之间普遍存在误差,实验中夹具与试件之间的摩擦、试件制作产生的缺陷、试件厚度引起的失稳都会影响实验结果.其中,C3、D3、E3、F3工况的误差较大,主要是因为层合板在实验加载过程中发生的扭转现象导致计算所得修正后的断裂韧性实验值出现较大误差,如图4所示.因此,在实际工程应用中不可忽略扭转导致的误差. 图4 实验中扭转现象Fig.4 Torsion phenomenon in the experiment 同时,对比多向层合板的断裂韧性(旧模型)、考虑90°子铺层和纤维脱粘的断裂韧性(修正模型)与实验值可以看出,修正模型的误差要低于旧模型的误差,而且当复合材料层合板厚度越厚时修正模型精度越高.因此,90°子铺层对断裂韧性的影响不能忽略. 综上所述,考虑90°子铺层和纤维脱粘的断裂韧性计算方法对厚度较厚的复合材料层合板有一定的修正作用.相比多向层压板的断裂韧性计算方法,本文所提方法不仅考虑90°子铺层的断裂韧性,还考虑断裂过程中纤维脱粘所释放的能量,更适用于所有铺层方式的纤维增强复合材料层合板,并且提高了计算的精度. 用S-4700S扫描电镜对T300/69复合材料层合板试样进行SEM观测,主要对裂纹起始区和扩展区分别进行200倍和600倍的断口形貌观测,可以得到6种不同铺层方式下SEM观测图片,如图5所示. 由图5可以看出:在垂直于裂纹的拉应力作用下,90°子铺层主要为基体断裂,纤维平行于裂纹方向,因而断口较为整齐;而0子铺层主要表现为纤维断裂,且纤维并不是直接沿断口整齐地发生断裂,说明纤维与基体间存在的粘结作用导致纤维被拉伸出基体一段长度后才发生断裂. 由图5还可以看出:同样在垂直于裂纹的拉应力作用下,±45°子铺层的断口形貌与正交层合板的断口形貌略有不同;±45°子铺层的纤维和基体都没有呈现非常整齐的断口,随着层数的增加基体与纤维的粘结现象更为严重.与图5a~5c的3种正交层合板相比,图5d~5f的3种铺层方式层合板中90°子铺层添加了部分增强体.由此说明,铺层方式越复杂强度越高. 基于不同条件下断口形貌细观分析6种铺层方式,可以看出:受到垂直纤维方向的应力作用时,尽管90°子铺层的断裂韧性非常小,但90°子铺层断裂时仍会出现少量的纤维断裂;并且在对称铺设的层合板中,90°子铺层数量增加导致层合板的厚度增厚,进而影响整个层合板的断裂韧性.因此,考虑90°子铺层的断裂韧性对层合板整体断裂韧性有一定的修正作用. 本文以T300/69纤维增强复合材料层合板为研究对象,通过对多向层压板的断裂韧性理论进行研究,发现传统复合材料层合板断裂韧性计算方法在特殊情况下存在一定误差,因而提出考虑90°子铺层的断裂韧性计算方法.该方法对较厚的正交层合板有一定的修正作用,并且考虑了非正交铺层层合板裂纹扩展时纤维与基体的脱粘现象.利用ABAQUS有限元软件进行了模拟计算,将考虑90°子铺层和纤维脱粘的断裂韧性计算方法与紧凑拉伸实验结果进行对比,得出以下结论: 1) 通过紧凑拉伸实验,利用载荷-位移数据和有限元计算的归一化能量释放率,得到不同铺层方式下复合材料层合板的断裂韧性.利用扫描电镜观察断口形貌,可以看出,纤维增强复合材料层合板随着裂纹逐渐扩展和层合板厚度不断增厚90°子铺层对层合板整体的影响愈发明显,同时纤维脱粘现象也会影响复合材料层合板整体断裂韧性. 2) 考虑90°子铺层和纤维脱粘的断裂韧性计算方法是基于多向层压板的断裂韧性计算方法,通过不同铺层方式下90°子铺层和纤维脱粘时所释放的能量对断裂韧性公式进行修正.结果表明,该方法的计算结果与实验结果更接近.3.3 计算考虑90°子铺层和纤维脱粘的断裂韧性
3.4 实验验证

4 断口形貌分析
5 结论
