广义Rickart模
2024-01-06王永铎任玉芳
王永铎, 任玉芳
(兰州理工大学 理学院, 甘肃 兰州 730050)
贯穿全文,环R都是有单位元的环,模都是右R-模.对于右R-模M,S=EndR(M)表示M的自同态环.对于任意的φ∈S,Kerφ表示φ的核,Imφ表示φ的像.用N≤M,N≤⊕M,L≅N分别表示N是M的子模,N是M的直和项,L和N同构.E(M)表示M的内射包,R(n)表示R的n次直和.记
rM(φ)={m∈M|φm=0}rS(I)={φ∈S|Iφ=0}rR(N)={r∈R|Nr=0}
其中φ∈S,I是S的任意非空子集,N≤M.
Lee等[1]引入了Rickart模的概念.称M是Rickart模,如果S中的任意元素在M中的右零化子由S的幂等元生成.证明了环R是半单阿廷环当且仅当所有右R-模是Rickart模当且仅当所有extending右R-模是Rickart模当且仅当所有内射右R-模是Rickart模当且仅当所有内射右R-模是Baer模.Wilson[2]提出了SIP模的概念.称模M为SIP模,如果M的任意一对直和项的交是M的直和项.Tasdemir等[3]引入了广义SIP模(简称GSIP模)的概念.称模M为GSIP模,如果M的任意一对直和项的交同构于M的直和项.受文献[1-3]的启发,本文中引入了广义Rickart模的概念.称M是广义Rickart模,如果S的任意元素在M中的右零化子同构于M的直和项.给出了是广义Rickart模但不是Rickart模的例子,并研究了广义Rickart模的一些性质,证明了环R是半单阿廷环当且仅当所有右R-模是广义Rickart模.
1 预备知识
称M是virtually半单模[4],如果M的任意子模同构于M的直和项.称R是右遗传环[5],如果R的每个右理想都是投射的.称M是不可分解模{5],如果M≠0且M只有平凡的直和项.称模M是内射模[5],如果对任意的单同态f:N→K以及R-模同态g:N→M均有模同态h:K→M使得hf=g.称M是Baer模[6],如果S的任意非空子集的右零化子由S的幂等元生成.称R是右V-环[7],如果任意单右R-模是内射模.称M是有限余生成模[7],如果M的基座是有限生成的且在M中本质.称M是有限余表示模[7],如果M满足:
1)M是有限余生成的;
2) 若在正合列0→M→L→N→0中L是有限余生成的,则N也是有限余生成的.称M是extending模[8],如果M的任意子模都是其直和项的本质子模.
2 主要结果
定义1设M是右R-模,S=EndR(M).称M是广义Rickart模,如果S的任意元素在M中的右零化子同构于M的直和项,即对于任意的φ∈S,存在e2=e∈S,使得
rM(φ)=Kerφ≅eM
注意Kerφ=rM(φ),φ∈S.
例1Virtually半单模是广义Rickart模.
证明设M是virtually半单模,对于任意的φ∈EndR(M),因为M的任意子模同构于M的直和项,所以Kerφ同构于M的直和项,即M是广义Rickart模.
Rickart模是广义Rickart模,但是广义Rickart模不一定是Rickart模.

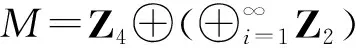
定义2称M满足H3条件,如果对M的任意直和分解M=L⊕N,C≤L,D≤⊕M,由C≅D可推出D≤L.称满足H3条件的模为H3模.
例3不可分解模是H3模.
命题1H3模的直和项是H3模.
证明设M是H3模,M=L⊕N.令N=A⊕B,C≤A,D≤⊕N,且C≅D,那么M=L⊕N=A⊕(B⊕L),D≤⊕M.因为M满足H3条件,所以D≤A,因此N是H3模.
定理1设M是广义Rickart模,且满足H3条件.则M的直和项是广义Rickart模.
证明设M是广义Rickart模,N≤⊕M,存在e2=e∈EndR(M),即N=eM,φ∈EndR(N).需要证Kerφ同构于N的直和项.令M=L⊕N,φ′=φ⊕1L.从而自同态φ:eM→eM可扩展到自同态φ′:L⊕N→L⊕N,即φ′:M→M.因为
Kerφ′= Kerφ
M是广义Rickart模,所以
Kerφ≅A≤⊕M
因为M满足H3条件,所以由M=L⊕N,Kerφ≤N,A≤⊕M,Kerφ≅A,可推得A≤N.从而A≤⊕N,进而Kerφ≅A≤⊕N,故N是广义Rickart模.
注1设M是广义Rickart模,且满足H3条件,φ∈EndR(M).若φ是幂等元,则有M=Kerφ⊕Imφ,根据定理1可知,Kerφ和Imφ都是广义Rickart模.
定义3称M满足广义D2条件,如果对任意的N≤M,由M/N同构于M的直和项可推出N同构于M的直和项.称满足广义D2条件的模为广义D2模.
命题2设M是模.若对于任意的φ∈EndR(M),Imφ同构于M的直和项.则以下条件等价:
1)M是广义D2模;
2)M是广义Rickart模.
证明1)⟹2) 设M是广义D2模.对于任意的φ∈EndR(M),由模同态基本定理可知,M/Kerφ≅Imφ,因为Imφ同构于M的直和项,所以M/Kerφ同构于M的直和项.又因为M是广义D2模,所以Kerφ同构于M的直和项,因此M是广义Rickart模.
2)⟹1) 设M是广义Rickart模,N≤M,且M/N≅L≤⊕M.存在φ∈EndR(M),使得Kerφ=N.因为M是广义Rickart模,所以N同构于M的直和项,因此M是广义D2模.
定义4[9]称M满足H1条件,如果A≤M,B≤M且A≅B,可推出M/A≅M/B.
命题3设M是广义Rickart模.若M满足H1条件,则对于任意的φ∈EndR(M),Imφ同构于M的直和项.
证明设任意的φ∈EndR(M).因为M是广义Rickart模,所以
Kerφ≅M′≤⊕M
记M=M′⊕N.又因为Kerφ≤M,M′≤M,且M满足H1条件,所以
M/Kerφ≅M/M′≅N≤⊕M
由模同态基本定理可知:
M/Kerφ≅Imφ
因此Imφ同构于M的直和项.
称M是morphic模,如果对于任意的φ∈EndR(M),
M/Imφ≅Kerφ
命题4设M是满足H1条件的morphic模.若对于任意的φ∈EndR(M),Imφ同构于M的直和项,则M是广义Rickart模.
证明设Imφ≅M′≤⊕M,记M=M′⊕N.因为Imφ≤M,M′≤M,且M满足H1条件,所以
M/Imφ≅M/M′≅N≤⊕M
又因为M是morphic模,所以M/Imφ≅Kerφ,因此Kerφ同构于M的直和项,即M是广义Rickart模.
定理2广义Rickart模是GSIP模.
证明设M是广义Rickart模.令L=eM,N=fM,非零幂等元e,f∈EndR(M),M=L⊕L′=N⊕N′.那么
Ker(1-f)e=[eM∩Ker(1-f)]⊕(1-e)M= (eM∩fM)⊕(1-e)M= (L∩N)⊕L′
因为M是广义Rickart模,所以
(L∩N)⊕L′≅M′≤⊕M
即存在同构φ:(L∩N)⊕L′→M′,使得
φ(L∩N)+φ(L′)=M′
因为
φ(L∩N)∩φ(L′)=0,所以
φ(L∩N)⊕φ(L′)=M′
因此φ(L∩N)是M′的直和项.因为M′≤⊕M,所以φ(L∩N)≤⊕M.又因为L∩N≅φ(L∩N),所以L∩N同构于M的直和项,因此M是GSIP模.
由定理2可知广义Rickart模是GSIP模,那么根据文献[3]中的定理2.2和2.3可得以下两个推论.
推论1若M是广义Rickart模,则对于M的任意一对直和项L和N,投影映射φ:M→N,限制映射φ|L的核同构于M的直和项.
推论2若M是广义Rickart模,则对于M的任意直和分解M=L⊕N,任意同态φ:L→N,Kerφ同构于M的直和项.
设M是右R-模.称M满足C2条件,如果N≤M,L≅N,且L≤⊕M,可推出N≤⊕M.
称M是准内射模,如果对于单同态f:N→M及任意同态g:N→M,存在同态g-:M→M,使得g-f=g.
称M是伪内射模,如果对于任意同态β:0→A→M和α:0→A→M,存在γ∈EndR(M),使得β=γα.
定理3设M是右R-模,且M满足C2条件.则以下条件是等价的:
1)M是广义Rickart模;
2)M是Rickart模.
推论3内射模(自内射模,准内射模,伪内射模)M是广义Rickart模当且仅当M是Rickart模.
定义5称M是广义N-Rickart模,如果对于任意同态φ:M→N,Kerφ同构于M的直和项.
根据定义5,右R-模M为广义Rickart模当且仅当M为广义M-Rickart模.
命题5设M是广义Rickart模,且满足H3条件,M1⊕M2≤⊕M.则Mi是广义Mj-Rickart模,对于任意的1≤i≠j≤2.
证明设φ∈HomR(Mi,Mj).令
N={(mi+φmi)|mi∈Mi}
则N≤⊕M,那么Kerφ=Mi∩N.因为M是广义Rickart模,由定理2知M是GSIP模,所以Kerφ=Mi∩N同构于M的直和项.记
Kerφ≅H≤⊕M
则存在M的子模L,使得
M=L⊕H,Kerφ≤Mi≤⊕M
因为M满足H3条件,所以H≤Mi.又因为
Mi∩M=Mi∩(L⊕H)
由模律可知
Mi=(Mi∩L)⊕(Mi∩H)=(Mi∩L)⊕H
从而H≤⊕Mi,所以Kerφ同构于Mi的直和项,因此Mi是广义Mj-Rickart模,对于任意的1≤i≠j≤2.
定理4设R是环.则以下条件是等价的:
1) 所有右R-模是广义Rickart模;
2) 所有extending右R-模是广义Rickart模;
3) 所有内射右R-模是广义Rickart模;
4) 所有内射右R-模是Baer模;
5)R是半单阿廷环.
证明1)⟹2)⟹3)是显然的.
3)⟹4) 设右R-模M是内射模.由于内射模都满足C2条件,因此M是满足C2条件的广义Rickart模,故由定理3知M是Rickart模.由文献[1]中定理2.25知,所有内射的Rickart模是Baer模.
4)⟹5) 由文献[6]中定理2.20可得.
5)⟹1) 由文献[1]中定理2.25知所有右R-模都是Rickart模,所以所有右R-模都是广义Rickart模.
引理1[7]设R是环.则以下条件等价:
1)R是右V-环;
2) 所有有限余生成R-模是半单模;
3) 所有有限余表示R-模是内射模.
定理5设R是右遗传环.则以下条件等价:
1)R是右V-环;
2) 所有有限余生成R-模是广义Rickart模;
3) 所有有限余表示R-模是广义Rickart模.
证明1)⟹2) 由文献[7]中引理23.1可得.
2)⟹3) 由定义可知,如果M是有限余表示模,那么M是有限余生成模,因此由2)知所有有限余表示R-模都是广义Rickart模.
3)⟹1) 设M是有限余表示R-模.由文献[7]中的命题30.1知,E(M)和E(M)/M是有限余生成的.从而由文献[7]中命题21.4可知,E(M)⊕E(M)/M是限余生成的.因为R是右遗传环,所以内射模的商模是内射模,从而E(M)/M是内射模.又因为内射模的有限直和是内射模,所以E(M)⊕E(M)/M是内射模.因为有限余生成内射模是有限余表示的,所以E(M)⊕E(M)/M是限余表示R-模,从而E(M)⊕E(M)/M是广义Rickart模,由推论2可知,对于自然满同态φ:E(M)→E(M)/M,Kerφ=M同构于E(M)⊕E(M)/M的直和项.因为内射模的直和项是内射模,所以M同构于内射模.因此由引理1可知,R是右V-环.
3 结论
本文对Rickart模进行推广, 给出广义Rickart模的概念, 研究了广义Rickart模的一些性质,证明了广义Rickart模是GSIP模;所有右-R模是广义Rickart模的环R是半单阿廷环; 满足H3条件的广义Rickart模的直和项是广义Rickart模等.本文的研究使得模类更加丰富,同时希望能够为进一步研究环与模提供新的方法和思路.
