一类多参数不确定非线性级联系统的自适应稳定控制
2024-01-06何秋锦
何秋锦, 张 健
(1. 广州城市理工学院 计算机工程学院, 广东 广州 510800; 2. 郑州大学 数学与统计学院, 河南 郑州 450001)
不确定非线性系统因其系统模型的一般性,更符合实际工程建模的需要,一直都受到国内外学者的广泛关注.有关该类系统的分析和综合问题,目前已取得了很多有意义的研究成果,其中最为常见的控制设计方法有鲁棒控制、自适应控制以及结合两者优点的鲁棒自适应控制[1].特别是Kanellakopoulos等[2]、张强等[3]、Liu等[4]提出的Backstepping方法,其利用系统的结构特性递推构造整个系统的Lyapunov函数,使得控制器的设计结构化、系统化,已成为处理非线性系统控制问题的主要方法之一.该方法消除了经典无源设计中系统相对阶为1的限制,放宽了系统非线性项的增长性条件和匹配性条件,能更有效解决具有下三角结构的非线性级联系统[5]的控制设计问题.特别是,结合了自适应设计思想的自适应Backstepping方法可有效地处理系统中存在的不匹配不确定项,其将系统分解成若干个子系统,然后为每一个子系统设计相应的Lyapunov 函数、虚拟控制器以及适当的参数自适应更新律,迭代直至最终完成实际控制器的构造以确保整个闭环系统满足预期的控制目标.
一般来说, 在系统建模过程中难免要考虑实际工程环境对系统的各种约束,例如常见的系统输入饱和、状态或输出受限以及其他为了保证系统性能或安全提出的一些约束条件,如果在建模中不考虑这些约束条件, 将会降低所设计控制器的性能甚至破坏系统[6].此外,约束条件的提出不仅是因为实际工程的需要,而且也有理论上的必要,如在用人工神经网络逼近未知函数时,须限制未知函数的自变量在一个有界集中以确保逼近的有效性[7].在处理非线性系统中的约束条件时,可考虑利用约束区间构造Backstepping方法中所需的Lyapunov函数,即所谓的障碍Lyapunov函数.不同于常见的在整个状态空间上有定义且径向无界的Lyapunov函数,障碍Lyapunov函数在受约束量趋向于约束区间边界时,函数值将趋向于无穷大.故而,只要所构造的障碍Lyapunov函数沿着系统的轨迹是有界的,那么就可避免在系统运行中违背这些约束条件,从而保证受约束量始终在约束区间内.通常的障碍Lyapunov函数可分为对称和非对称两种情形,后者可允许约束变量的初值约束区间是非对称的.利用基于障碍Lyapunov函数的Backstepping方法,可解决输出受限以及全状态受限等多种情况下非线性系统的综合问题,目前已有很多有意义的研究成果[8-10].
此外,实际工程系统中的执行器、传感器或者部分组件难免会发生故障,这会造成系统性能恶化甚至于发生事故[11-13].系统容错控制就是在考虑系统发生故障的情况下设计控制器,以提高系统可靠性并保证在所有可能情况下的系统稳定性.容错控制一般可分为被动式和主动式,前者是一种针对先验故障集的鲁棒控制技术,而后者则是通过在线的故障检测和诊断实时配置控制器,以维持整个闭环系统的稳定性以及实现预期的性能指标.容错控制目前已经广泛地应用到各类系统的控制设计中,特别是针对执行器故障模型,目前已取得很多丰富的结果[12-15].然而,在已有执行器故障相关文献中[12-15],尽管涉及到自适应控制问题,但很少考虑系统受限的情况.正如前文所述,系统存在约束条件是难免的、必要的,在该情况下研究具有执行器故障的自适应控制问题是有理论和实际研究价值的.
因此,本文针对一类具有多个未知参数的非线性级联系统,在系统具有状态约束和执行器故障的情况下,研究其自适应状态反馈稳定控制问题.具体而言,利用自适应Backstepping方法,基于系统的状态反馈信息设计自适应控制器使闭环系统达到期望的稳定控制目标,即闭环系统的所有状态有界,且原系统的状态不仅满足指定的受限约束条件,还渐近收敛于原点.值得指出的是,本文利用光滑投影算子设计系统未知参数的在线估计更新律,其可确保在Backstepping迭代设计中对参数更新律可导的要求[16-17],并能有效地处理由系统未知参数带来的控制设计难点.通过基于Lyapunov函数的稳定性分析,证明所设计的自适应状态反馈控制器达到预期的稳定控制目标.本文贡献主要在于提出了一种有效地结合光滑投影算子、障碍Lyapunov函数的自适应设计策略,成功地解决一类具有执行器故障和全状态受限的不确定非线性级联系统的稳定控制问题.所得理论结果,拓展了鲁棒自适应Backstepping设计方法的适用范围,丰富了非线性控制设计理论.
1 问题描述及预备知识
本文考虑一类由以下微分方程组描述的多参数非线性级联系统[5](Nonlinear Cascade System):
(1)

同时,考虑系统⑴存在执行器故障,即控制u为容错控制器,具体的执行器故障模型如下:
u(t)=μ(t)ν(t)+δ(t)

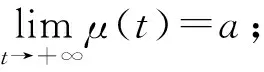
不失一般性,类似于文献[12-15],本文对执行器故障模型做如下假定:

具体而言,本文的控制目标是:设计适当的自适应状态反馈控制输入ν,以确保系统(1)对应的闭环系统所有状态有界,状态x满足受限约束条件且渐近收敛到原点.为实现控制目标,必须处理系统(1)中未知向量参数θ带来的设计困难.为此,本文引入如下基于光滑投影算子的自适应参数更新律:
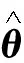
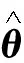
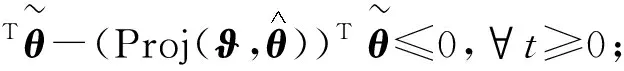
2 非线性自适应状态反馈稳定控制设计策略
本文采用Backstepping迭代设计框架解决系统(1)的自适应状态反馈稳定控制问题.具体而言,基于李雅普诺夫(Lyapunov)稳定性分析理论,利用投影算子逐步设计虚拟控制器以及相应的参数更新律以保证每一步子系统的稳定性,并最终在第n步构造出整个系统的实际控制律v以确保闭环系统达到期望的控制目标.为此,首先引入如下坐标变换:
(2)
式中:αi,i=1,…,n-1是待设计的虚拟控制器,将在相应步的迭代设计中给出具体的表达形式.
步骤1取候选Lyapunov函数:
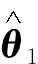
故基于变换(2)的定义,有
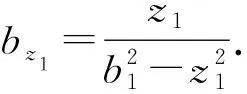
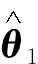
从而有式(3)成立:
(3)
注2选择适当的虚拟控制器在Backstepping迭代设计中不可或缺,若系统维度n=1,即x2是待设计的控制输入,则令x2=α1即可.然而x2是系统状态,故迭代设计中引入变量z2=x2-α1作为变量x2对虚拟控制器α1的误差,并在下一步中分析其动力学行为.
步骤2由于z2=x2-α1,故有
将系统(1)代入,可得
令候选Lyapunov函数:
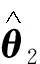


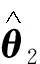
则类似于步骤1可有式(4)成立:
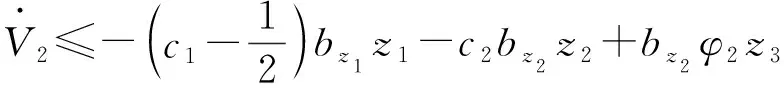
(4)

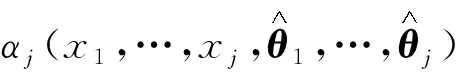
(5)
式中:候选Lyapunov函数:
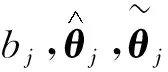
由系统(1)可知:
取候选Lyapunov函数:

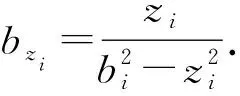
(6)
可得



可得
即第i(3≤i≤n-1)步迭代设计完成.
步骤n由上面迭代设计可知,当i=n-1时,有式(7)成立,
(7)
式中:zn=xn-αn-1.故由系统(1)可知:
取候选Lyapunov函数:
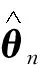
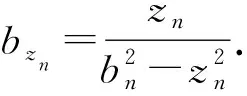
则类似于前述步骤,由第一节给出的投影算子的性质2)并注意到u为容错控制器,即u=μ(t)ν(t)+δ(t),可得
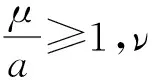
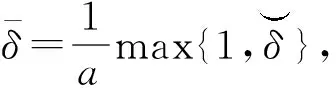
(8)
进而有
其中:σ(t)>0且σ(t)∈L[0,+∞),即
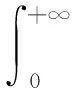
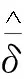
(9)
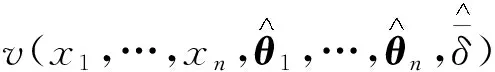
(10)
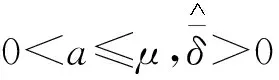
(11)
(12)
第n步的设计完成,基于上述迭代设计,给出如下定理以刻画本文的主要结果.
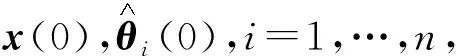
证明对任意t>0,将式(12)两边在区间(0,t)上积分可得
(13)
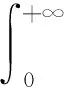
∀t≥0
(14)
此外,由式(13)以及参数ci(i=1,…,n)的选择方式可知:

3 仿真算例
通过两个算例仿真验证本文所得理论结果的正确性和有效性.
算例1考虑以下二阶非线性级联系统
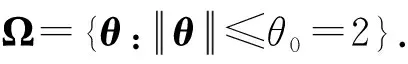
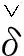
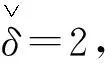
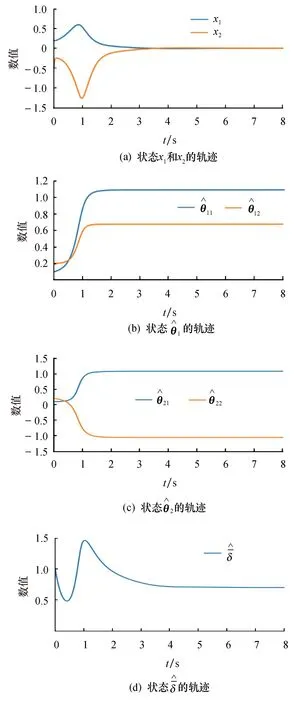
图1 闭环系统状态轨迹图Fig.1 The trajectories of closed-loop system states
造控制器的作用下,闭环系统达到预期的控制目标.
算例2考虑如图2所示的受控平面单摆系统[5],其动力学方程如下:
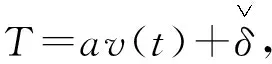
图2 平面单摆系统
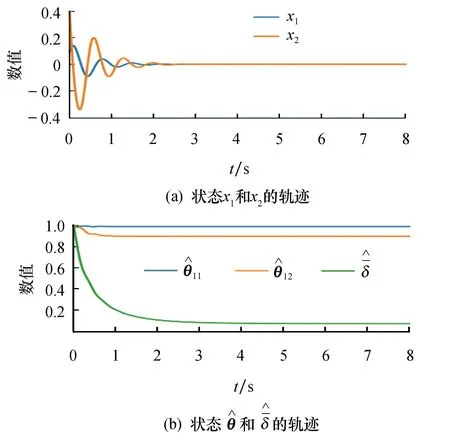
图3 时的闭环系统状态轨迹图
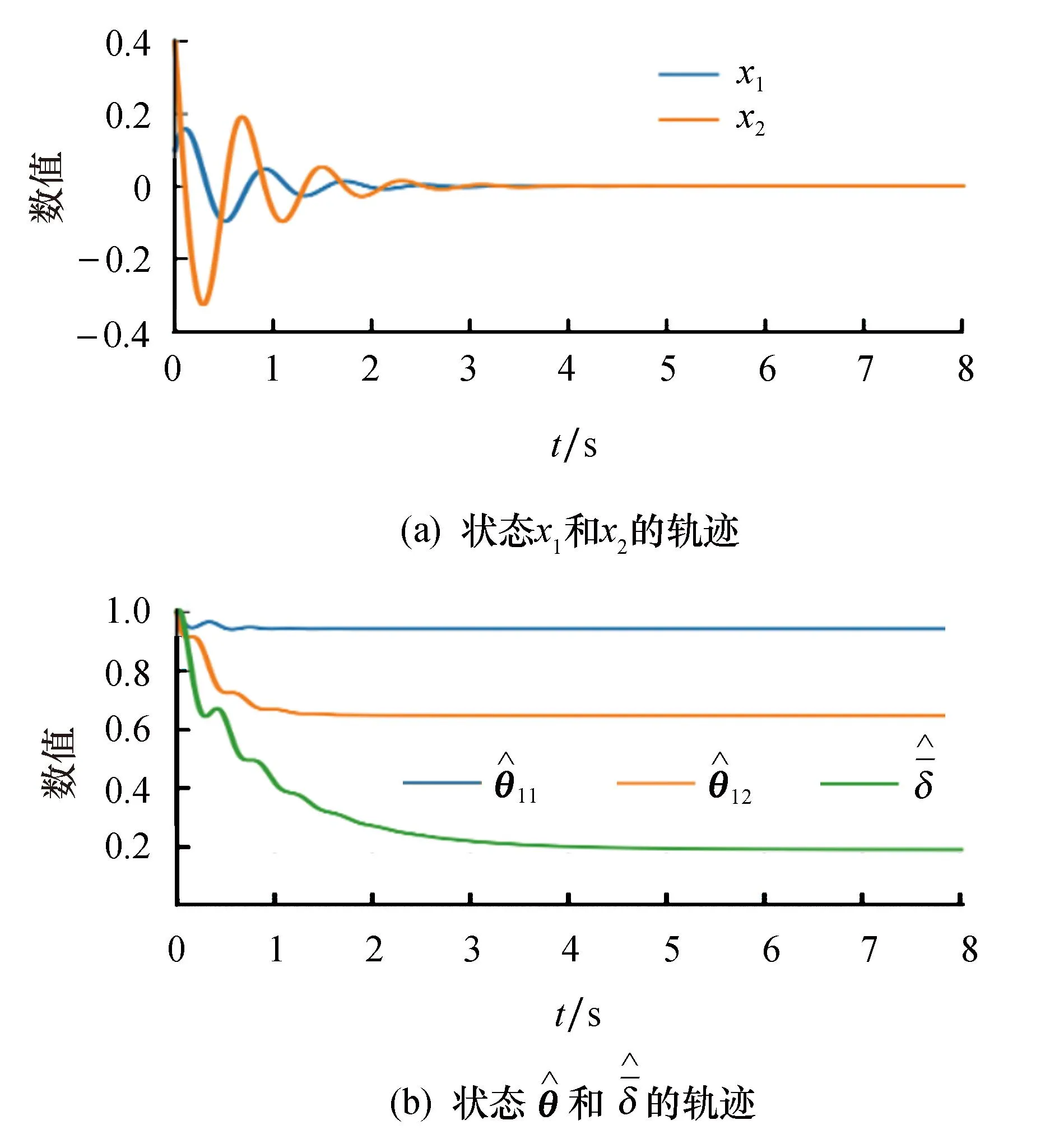
图4 时的闭环系统状态轨迹图Fig.4 The trajectories of closed-loop system states when
4 结论
本文解决了一类非线性级联系统的自适应状态反馈稳定控制问题.尽管系统存在向量参数化的不确定性、全状态受限约束以及具有未知性的执行器故障,但通过构造适当的障碍Lyapunov函数和基于光滑投影算子的自适应设计方法,成功地为系统设计了一个自适应状态反馈稳定控制器,其可确保闭环系统所有状态在时间区间(0,+∞)上一致有界,且原系统状态x(t)满足约束条件且渐近收敛到原点.然而,需要指出的是,本文控制设计要求系统所有状态都是可量测的,若仅系统输出可测时,如何设计相应的自适应输出反馈稳定控制器也是一个非常有意义的问题,这是进一步的研究方向.
