盐雾环境下基于Weibull分布的钢筋混凝土腐蚀劣化行为

2024-01-06王彦鹏王子健汪丽娟刘吉林张云升

兰州理工大学学报 2023年6期

王彦鹏, 王子健, 汪丽娟, 刘吉林, 冯琼, 张云升

(1. 甘肃建投绿色建材产业发展集团有限公司, 甘肃兰州 730000; 2. 甘肃建投商品混凝土有限公司, 甘肃兰州 730060; 3. 甘肃省建设投资(控股)集团有限公司, 甘肃兰州 730050; 4. 兰州理工大学土木工程学院, 甘肃兰州 730050)

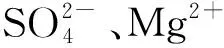
鉴于此,国内外学者开展了大量研究.刘军等[6]和陆春华等[7]通过喷洒浓度5%的氯化钠溶液模拟大气盐雾环境,研究了盐雾环境下混凝土的损伤劣化规律.Huang等[8]研究了珊瑚骨料混凝土在盐雾环境中的氯离子扩散行为,并建立了氯离子浓度峰值计算模型.苏林王等[9]和蒋一星等[10]对混凝土梁进行了盐雾环境与疲劳交变荷载耦合的加速腐蚀试验,描述了混凝土在盐雾与交变荷载共同作用下的损伤劣化规律.Xie等[11-13]通过盐雾碳化双重作用,研究了碳化对混凝土氯离子扩散性能的影响.综上所述,目前针对盐雾环境下混凝土的性能劣化行为研究取得了一些进展.然而,现有研究中盐雾溶液的选用主要参照标准进行(5%的NaCl溶液),未考虑实际环境中多种腐蚀离子共同存在且相互作用的问题,因此,大部分研究结果对于实际工程中钢筋混凝土腐蚀劣化防治具有理论指导意义,但缺少实际指导意义.

基于此,本文根据西部盐渍土地区土壤中实际腐蚀离子含量,配制复合盐溶液,设计盐雾与烘干耦合的加速腐蚀试验,进而模拟西部地区大气腐蚀环境;以腐蚀电化学参数和混凝土损伤度为性能劣化指标,结合钢筋腐蚀形貌分析,研究钢筋混凝土在盐雾环境下的损伤劣化规律;借助Weibull分布函数建立钢筋混凝土损伤劣化模型,进而对其寿命进行预测.

1 试验

1.1 试验材料

水泥采用P·O42.5水泥;砂采用细度模数为3.3的机制砂;石子采用最大粒径31.5 mm碎石;Ⅱ级粉煤灰,减水率为24%的高效减水剂;试验用水为自来水.具体配合比见表1.

表1 混凝土配合比

1.2 试验材料

根据表1制备100 mm×100 mm×100 mm钢筋混凝土试件,长度100 mm(直径10 mm)的钢筋放置于试件正中部位,且外伸出25 mm,便于电化学测试.试件成型24 h后拆模,移至标准养护条件下养护至28 d后开始盐雾干湿循环加速腐蚀试验.

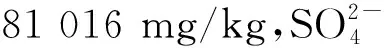
根据GB/T 50082—2009中相关规定,混凝土超声波声速与相对动弹模量E之间满足式(1)关系:

(1)

式中:E0为混凝土的初始动弹性模量;v0为混凝土的初始超声波声速;Et为t时刻混凝土的动弹性模量;vt为t时刻混凝土的超声波声速.

根据文献[14]定义,E降低到60%时混凝土为失效,进而定义经过t时间干湿循环后钢筋混凝土的损伤度Dt如式(2)所示.

(2)

式中:Dt的正常取值范围为[0,1],在此范围内表示钢筋混凝土未失效;当Dt≥ 1时,钢筋混凝土达到失效状态;当Dt≤ 0时,钢筋混凝土得到强化.

2 结果与分析

2.1 极化曲线结果与分析

由图1可知,随着干湿循环次数的增加,Ecorr在反复波动过程中先整体正向移动,后整体负向移动.在第0～80次干湿循环,Ecorr从初始的-0.314 V正向移动至-0.184 V,且阳极极化曲线比初始状态更加陡峭.根据标准 ASTMC876可知,当Ecorr<-126 mV时,钢筋腐蚀的概率仅为 10%;当Ecorr<-426 mV时,钢筋已出现严重腐蚀.因此可判断,干湿循环进行至第80次时,内部钢筋并未发生腐蚀,钝化膜反而更加稳定.

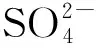
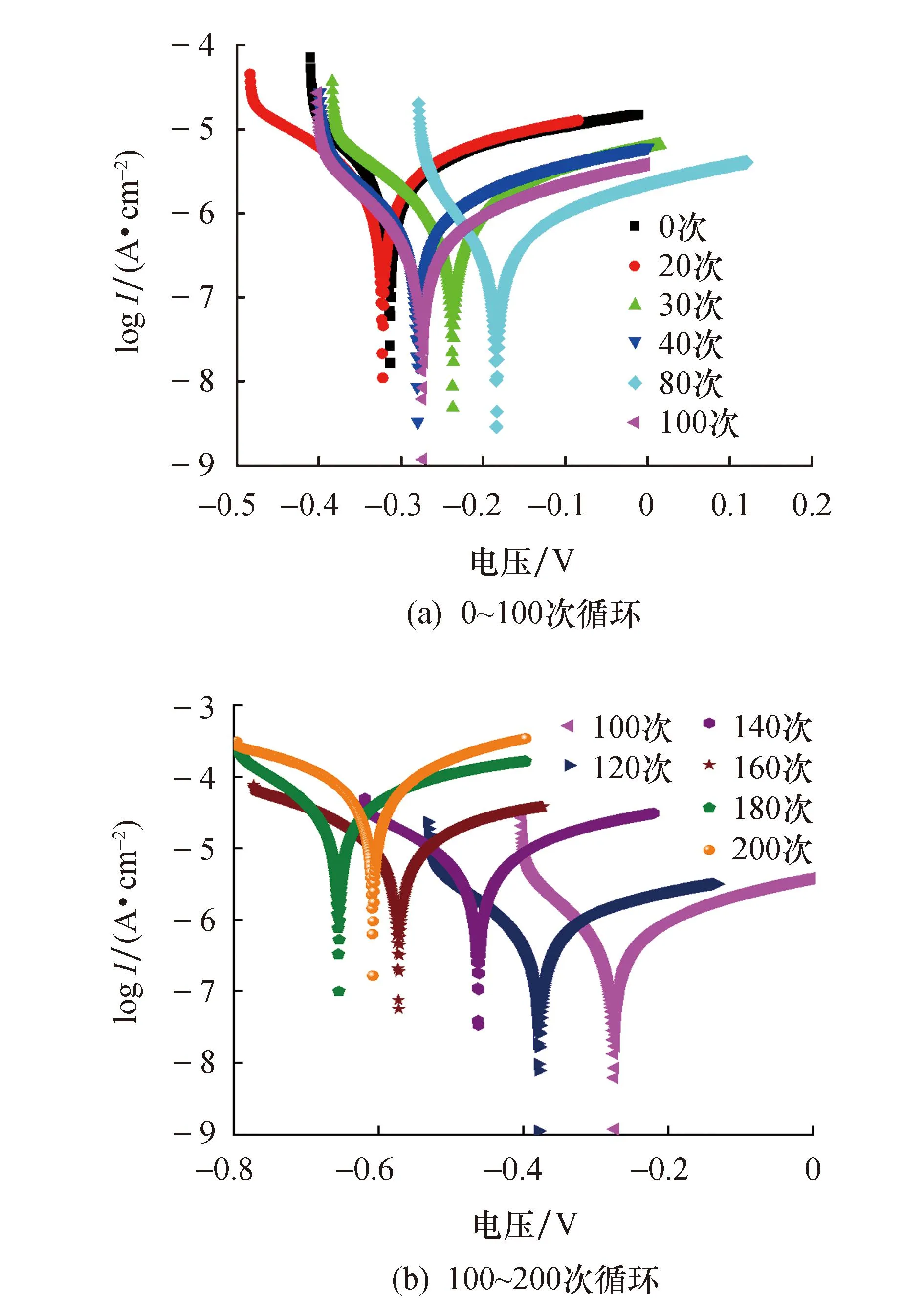
图1 钢筋混凝土极化曲线Fig.1 Polarization curves of reinforced concrete

在第 80～200 次干湿循环,极化曲线阳极陡坡逐渐减缓,当干湿循环进行到第 200 次时,达到与阴极基本相近的平稳状态,钝化区明显收缩,且Ecorr负向移动至-0.608 V.结合标准 ASTMC876规定可判断,此时内部钢筋已出现腐蚀.在极化曲线分析的基础上,利用电化学工作站自带软件对所有试件的极化曲线进行拟合获取icorr,将各组试件在各个干湿循环阶段下的icorr取平均值,绘制腐蚀电流密度随干湿循环次数的变化趋势图,结果如图2所示.

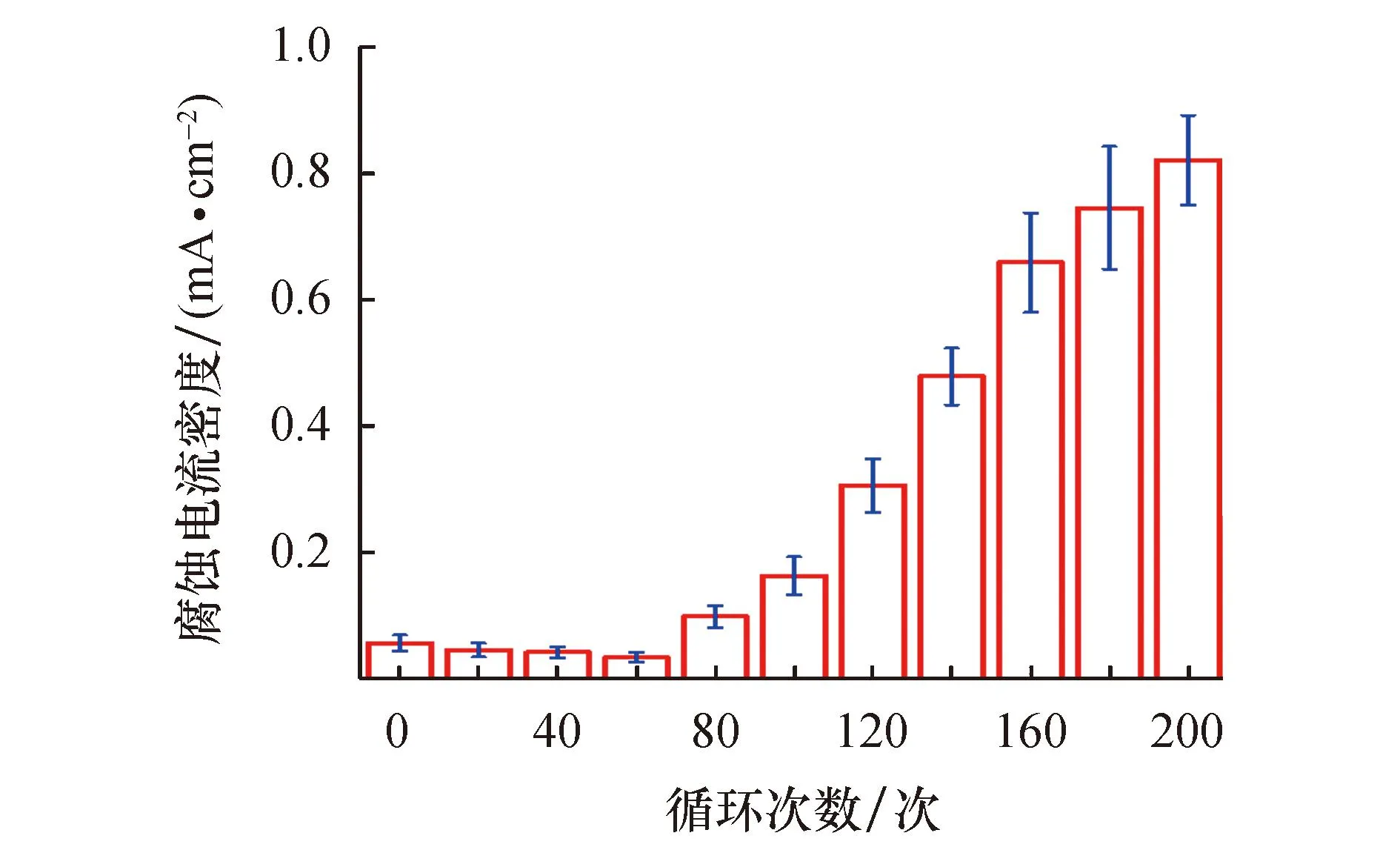
图2 腐蚀电流密度变化趋势Fig.2 The development trend of corrosion current density

由图2可知,随着干湿循环次数的增加,icorr先减小后快速增大,即试件内部钢筋的耐腐蚀性呈先强化后快速劣化的变化趋势.

在干湿循环0～60次,icorr处于较低水平,且有逐渐降低趋势.表2为腐蚀电流密度与钢筋腐蚀速率对应关系.由表2可知,钢筋处于钝化状态,且钝化膜随干湿循环次数的增加趋于稳定[16-17].而在干湿循环60次之后,icorr随干湿循环次数的增加逐渐增大;当循环进行至第100次时,icorr增大至0.163 μA/cm2,达到低腐蚀速率状态;当循环进行至第160次时,icorr增大至0.659 μA/cm2,已达到中等腐蚀速率状态;当循环进行至第200次时,icorr继续增大至0.821 μA/cm2.

表2 腐蚀电流密度与钢筋腐蚀速率对应关系

2.2 混凝土损伤度Dt结果与分析

盐雾干湿循环过程中混凝土损伤度Dt随干湿循环次数的变化规律如图3所示.由图3可知,随干湿循环次数的增加,Dt变化规律均可划分为2个阶段:1) 下降段:在干湿循环0～40次,Dt不仅未增大,反而降低为负值;2) 上升段:在干湿循环40～200次,Dt出现逐渐上升趋势,当进行到第200次时,Dt达到最大值0.668.分析其腐蚀破坏的机理可知,其混凝土损伤度变化规律是盐雾强化效应和劣化效应相互作用的结果.

图3 损伤度的变化趋势

综合认为,混凝土损伤度变化规律是盐雾强化效应和劣化效应相互作用的结果.干湿循环早期,强化效应大于劣化效应,表现为混凝土损伤度为负值;干湿循环中后期,劣化效应大于强化效应,表现为混凝土损伤度逐渐累积增大.

2.3 钢筋腐蚀形貌分析

切取干湿循环0次与200次试件内部的钢筋,采用场发射扫描电子显微镜对其进行线扫描分析,结果如图4a、b所示.由图可知,干湿循环0次时,钢筋表面0～200 μm处O元素的浓度低,Fe元素的浓度高,表明此时钢筋未被腐蚀;而干湿循环至200次时,钢筋表面0～55 μm处O元素的浓度较高,Fe元素的浓度较低,结合该阶段钢筋宏观形貌(图4c),可判断此时钢筋已出现腐蚀.

通过SEM对干湿循环200次时试件内部的钢筋腐蚀样品放大500倍,观测腐蚀产物微观形貌,并结合EDS分析确定腐蚀产物成分,结果如图5所示.

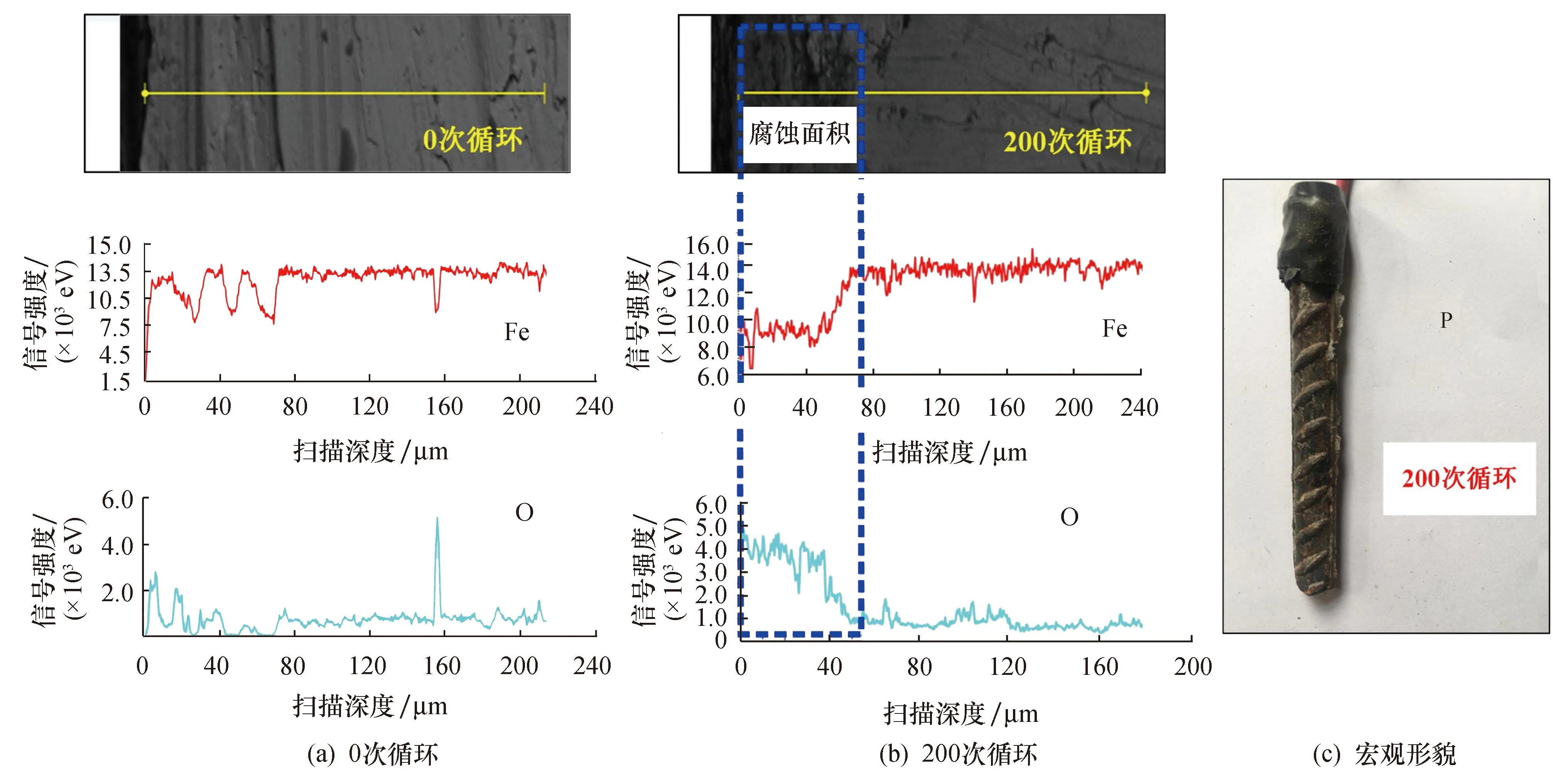
图4 钢筋线扫描图谱Fig.4 Line scan of steel bar

图5 钢筋表面腐蚀产物形貌

由图5a可知,当干湿循环至200次时,试件内部钢筋表面存在大量纤维状腐蚀产物,结构松散,且伴随着大量裂缝. 由图5b可知,此时钢筋表面O元素的质量分数为35.74%,Cl元素的质量分数为4.33%.结合钢筋表面形貌特征表明,盐雾中氯离子逐渐扩散抵达钢筋表面,导致钢筋腐蚀并生成铁氧化合物.

3 钢筋混凝土劣化模型的建立

3.1 Weibull函数理论基础

Weibull分布函数由瑞典工程师Waloddi Weibull在1951年首次提出,可通过小样本进行精确的寿命预测和可靠性分析[21-22],其包含位置参数、尺度参数和形状参数3个未知数[23],则其可靠度函数R(t)表达式如式(3)[24].考虑分布模型的复杂程度,本文取钢筋混凝土试件的位置参数γ=0,即假定钢筋混凝土劣化过程服从二参数Weibull分布,其R(t)则可简化为式(4).

式中:γ为位置参数(γ≥0);m为形状参数(m>0);θ为尺度参数(θ>0);t为钢筋混凝土劣化过程的记录值(t>γ).

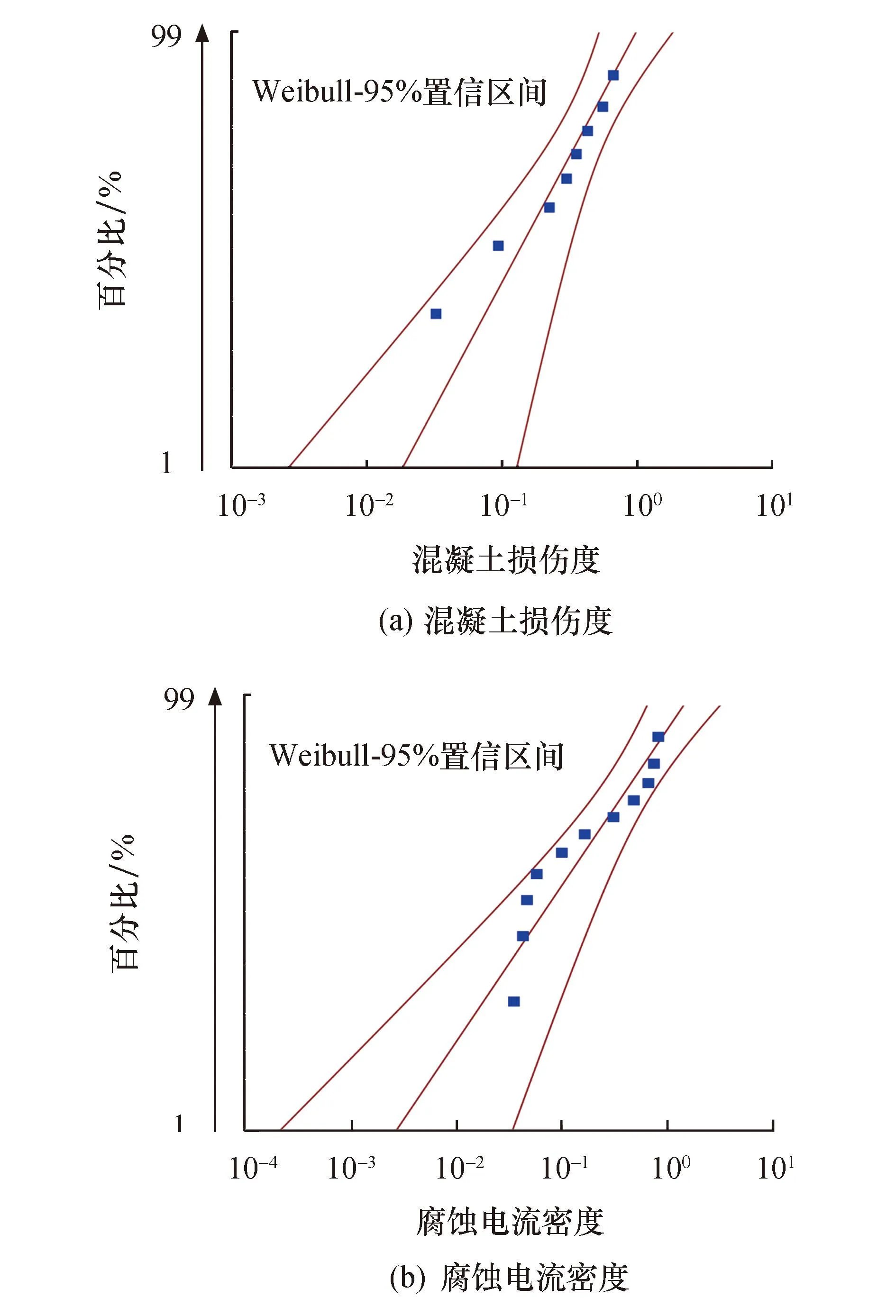
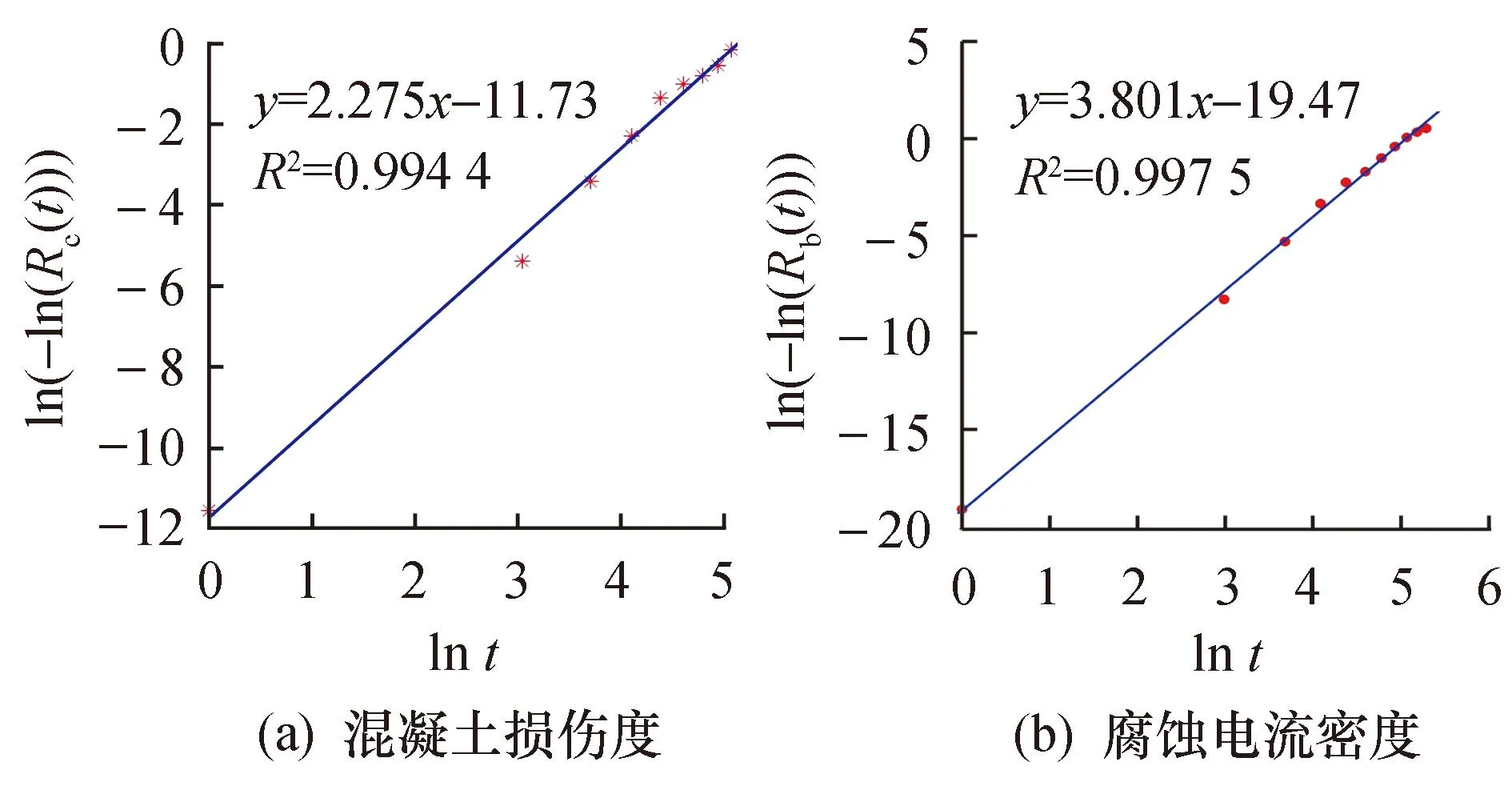
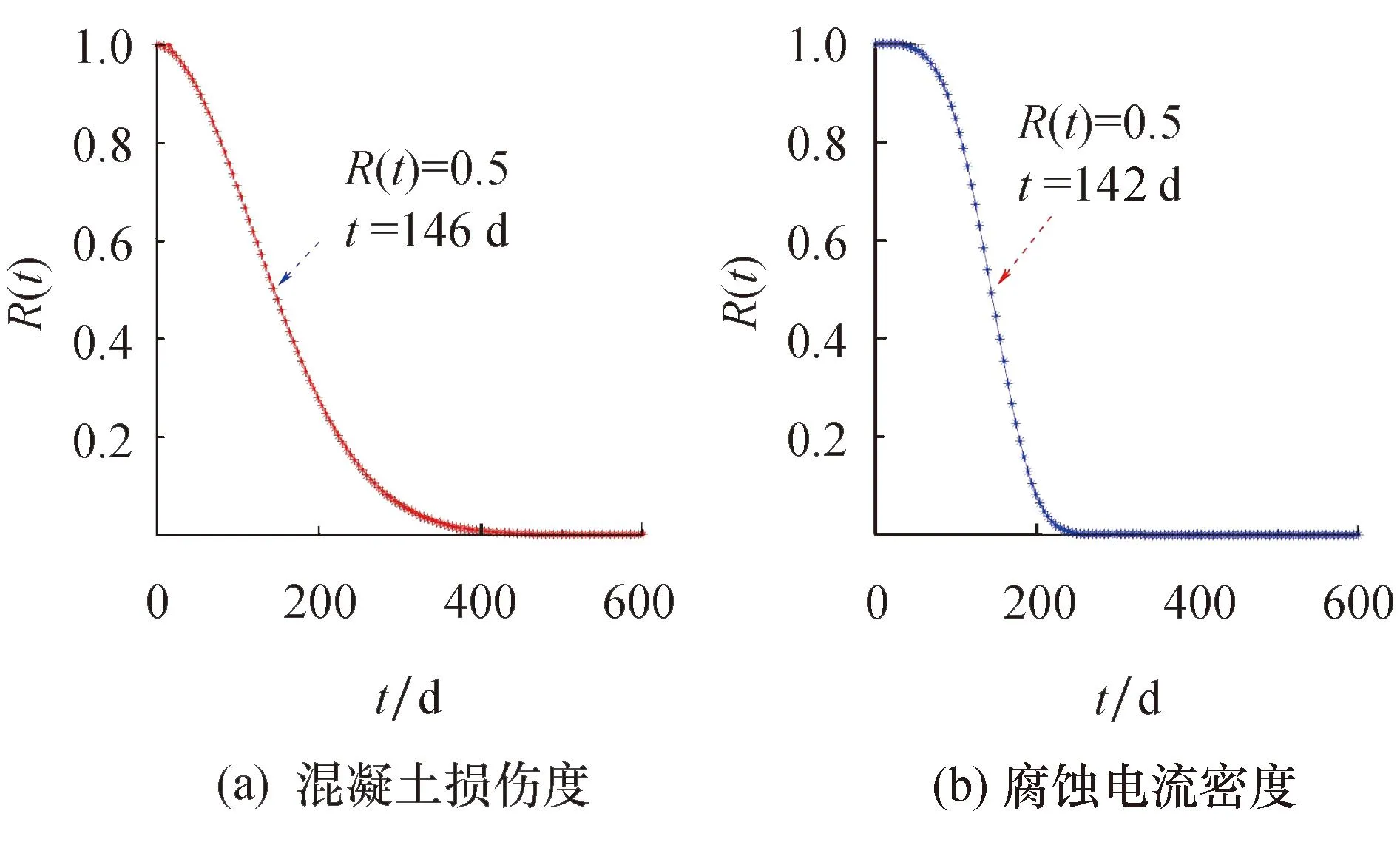
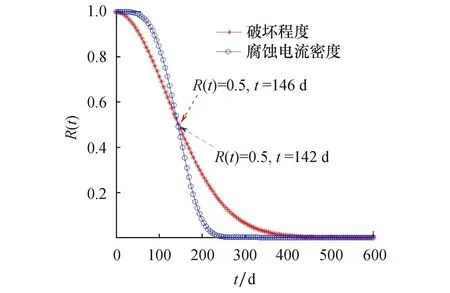
钢筋混凝土的可靠度与其劣化时间成反比,即可靠度随着劣化时间的增加而降低,直到完全失效,故0

3.2 劣化指标的Weibull分布假设检验

以混凝土损伤度Dt和腐蚀电流密度icorr作为样本信息,假设Dt和icorr随干湿循环次数的变化规律服从Weibull分布.利用Minitab软件对该假设进行检验,确定显著水平α为0.05,判断假设是否成立.其检验结果如图6所示.

图6 Weibull分布检验Fig.6 Weibull distribution test

由图6可知,试件在不同循环阶段的Dt和icorr均落在95%的置信区间,表明假设成立,即钢筋混凝土在盐雾干湿循环过程中,其Dt和icorr随干湿循环时间的变化规律均服从Weibull分布函数.

3.3 Weibull分布参数估计

1) Weibull分布参数估计方法

利用线性回归的最小二乘法进行参数估计,对于非线性的Weibull分布,需要经过一定的变换,具体步骤如下[25]:

将式(4)取双对数,整理可得:

ln(-ln(R(t)))=mlnt-mlnθ

(5)

令

y=ln(-ln(R(t))),x=lnt

a=m,b=-mlnθ

则式(5)可转换为

y=ax+b,m=a,θ=exp(-b/m)

(6)

如果x与y之间存在着较好的线性相关性,则Weibull分布的m和θ可以通过线性回归分析的方法来求解.

2) 劣化指标的Weibull分布参数估计

根据式(2)可知,当混凝土损伤度Dt>1时,钢筋混凝土失效,故某一时刻Dt对应的可靠度Rc(t)可用下式表示:

Rc(t)=1-Dt

(7)

由表2可知,钢筋混凝土内部钢筋icorr达到1.0 μA/cm2时,为高腐蚀速率状态,而对于某干湿循环阶段测得的icorr是不变的,因此某干湿循环阶段icorr对应的可靠度计算可用下式表示:

(8)

式中:icorr为某干湿循环阶段实测的icorr;im为钢筋高腐蚀速率状态时icorr的阈值,取1.0 μA/cm2.

将试件在干湿循环过程中不同循环阶段的Dt和icorr分别代入式(7)和式(8),计算出对应的可靠度Rc(t)和Rb(t),进而计算出式(5)中的yi=ln(-ln(Rc(ti)))、yj=ln(-ln(Rb(ti)))和对应的xi=ln(ti).通过最小二乘法进行线性回归分析,检验其线性相关性,具体回归分析结果如图7所示.

图7 回归分析结果Fig.7 Results of regression analysis

由图7可知,钢筋混凝土的ln(-ln(Rc(ti))) 和ln(-ln(Rb(ti)))分别与ln(ti)非常接近线性关系,相关系数R2分别为0.994 4和0.997 5,均接近于1,表明以Dt和icorr为劣化指标,采用Weibull分布函数建立劣化模型,可以有效地描述钢筋混凝土在盐雾干湿循环加速腐蚀过程中的损伤劣化过程.线性拟合系数a和b见表3.将a,b分别代入式(6),得试件Dt和icorr对应的Weibull分布函数的形状参数m和尺度参数θ,具体结果见表3.

表3 线性回归分析及参数估计结果

3.4 基于Weibull分布的钢筋混凝土劣化模型建立

将表3中的形状参数m与尺度参数θ分别代入式(4),得Dt和icorr对应的Weibull 分布可靠度函数,其可靠度函数曲线如图8所示.

图8 可靠度函数曲线Fig.8 Reliability function curve

由图8可知,在初始状态,即t=0时,钢筋混凝土没有损伤出现,钢筋混凝土内部钢筋处于钝化状态,此时可靠度R(t)=1.随着干湿循环次数的增加,混凝土损伤度不断累积,钢筋逐渐脱钝腐蚀,可靠度R(t)不断下降,最终,可靠度降低为0,表明钢筋混凝土失效.Dt和icorr分别在干湿循环146、142次时可靠度水平达到0.5,即达到中位寿命t0.5,与盐雾干湿循环加速腐蚀试验中Dt和icorr随干湿循环次数的实际演变结果相吻合.Dt和icorr分别将在干湿循环430、250次时可靠度水平降低为0,即完全失效.

3.5 钢筋混凝土的竞争失效分析

将Dt对应的Weibull分布可靠度函数曲线与icorr对应的Weibull分布可靠度函数曲线作对比,进而研究盐雾环境下钢筋混凝土的竞争失效问题,结果如图9所示.

图9 混凝土保护层与内部钢筋的竞争失效Fig.9 Competitive failure analysis of concrete cover and internal reinforcement

由图9可知,icorr对应的可靠度曲线在盐雾干湿循环加速腐蚀早期,即0～100 d阶段存在一个平台,可靠度保持为1;而Dt对应的可靠度曲线在干湿循环第100 d左右对应的可靠度为0.9.表明在盐雾环境干湿循环早期,混凝土保护层的劣化发展速度大于内部钢筋.

icorr对应的可靠度曲线和Dt对应的可靠度曲线分别在干湿循环第140 d左右相交.在此交点之前,Dt可靠度曲线一直位于icorr可靠度曲线左侧,即在此交点之前,Dt的劣化在钢筋混凝土的损伤劣化过程中占主导地位,而钢筋的腐蚀劣化占次要地位.随着干湿循环次数的增加,icorr可靠度曲线位于Dt可靠度曲线的左侧,即此时钢筋混凝土的损伤劣化由钢筋的腐蚀劣化占主导地位.由此可见,在盐雾干湿循环加速腐蚀过程中,混凝土损伤度的损伤诱导期较短,很快进入损伤加速期,但后期加速速度缓慢;而腐蚀电流密度的损伤诱导期较长,但是进入加速期后腐蚀发展迅速.