浑圆形裸脚式稀土矿山原地浸矿稳定浸润线分析
2024-01-06鲍建平桂勇罗嗣海王观石
鲍建平, 桂勇, 罗嗣海, 王观石
(1. 江西理工大学土木与测绘工程学院,江西 赣州 341000; 2. 赣南科技学院资源与土木工程学院,江西 赣州 341000;3. 矿山地质灾害预防控制与生态修复重点实验室,江西 赣州 341000; 4. 南昌航空大学,南昌 330063)
原地浸出工艺在我国南方离子型稀土矿中推广应用已有二十多年的历史[1],工艺的不足逐渐显现,主要体现在2 个方面:一是资源问题,表现在资源综合回收率偏低,据不完全统计,半数以上企业的资源综合回收率达不到75%[2-3];二是环境问题,表现在地质灾害频发,如江西龙南离子型稀土矿山因原地浸矿发生规模小、数量多的滑坡等地质灾害[4]。不同矿山具有不同的开采技术条件,需要进行专门的浸渗环节设计,但目前国内矿山生产管理粗放,常常简单套用一成不变的方法,甚至生搬硬套其他矿山的工艺和参数[5-6],是产生上述问题的主要原因。
研究表明,上述“资源-环境”问题均主要与矿山“注液-收液”的浸渗过程密切相关。浸渗过程的资源损失主要有浸矿盲区、母液渗漏和反吸附3 部分[7],其中,前2项损失主要是注液工程、收液工程布置不合理及注液强度不当引起的。浸矿液流经矿体会对矿体的抗剪强度产生弱化作用[8-9],尤其是当注液强度大于矿山的出渗能力时,矿山浸润面不断上升,当浸润面达到临界水位面以上时,即可在瞬间发生滑坡[10]。而浸润面的高低形状则取决于矿山的水文地质条件、渗透性能、注液强度与出渗能力等因素。
对“浸渗环节”,很多学者基于室内试验,在机理层面研究了浸矿过程的浸出动力学[11-13]与传质过程[14-17],以筛选浸矿剂[18-20]、优化浸矿工艺;部分学者基于矿山生产现场试验,研究了原地浸矿过程中矿山内浸润面、土水压力及边坡表面裂缝的变化规律[4,21],提出矿山滑坡的防控措施[22]。这些研究成果为浸渗环节“事中观测,事后总结”阶段提供了有力的帮助,但难以用于“事先预测(设计)”阶段。因此,池汝安等[23]指出,从矿山宏观水动力学角度研究浸取剂溶液在矿体内部的渗流规律,可以更好地指导离子型稀土矿的原地浸出。
本文选取浑圆形裸脚式稀土矿山为研究对象,建立原地浸矿“注液-收液”轴对称简化模型,基于地下水动力学和Dupuit 假定,在已知矿山地形条件及注液条件下推导矿山稳定浸润线方程,为原地浸矿浸渗环节的“事先预测(设计)”提供理论依据。
1 浑圆形裸脚式矿山原地浸矿稳定浸润线理论分析
1.1 矿山“注液-收液”轴对称简化模型
我国南方离子型稀土矿区多为低山丘陵地形,山头多为不规则的浑圆形[24]。离子型稀土矿原地浸出工艺注液工程一般为梅花形布置的注液孔,沿山顶往山腰的一定范围内布置,注液孔直径一般为Φ=0.15~0.30 m,深度一般为见矿0.5~1.0 m。收液工程则根据矿山具体的工程地质条件确定,其中,裸脚式矿山具有较完整的天然基岩底板,且在山脚或山谷处有基岩出露,常在山脚开挖集液沟收集母液[25],其工艺如图1 所示,图2 所示为江西某浑圆形稀土矿山照片。

图1 裸脚式稀土矿山原地浸出工艺示意Fig.1 Schematic diagram of the in-situ leaching process of a bare-foot rare earth mine

图2 江西某浑圆形稀土矿山Fig.2 A rounded rare earth mine in Jiangxi Province
对于浑圆形裸脚式矿山,沿过中心轴线截取剖面,可得到“注液-收液”轴对称简化模型,如图3 所示,对该模型作如下主要假设:
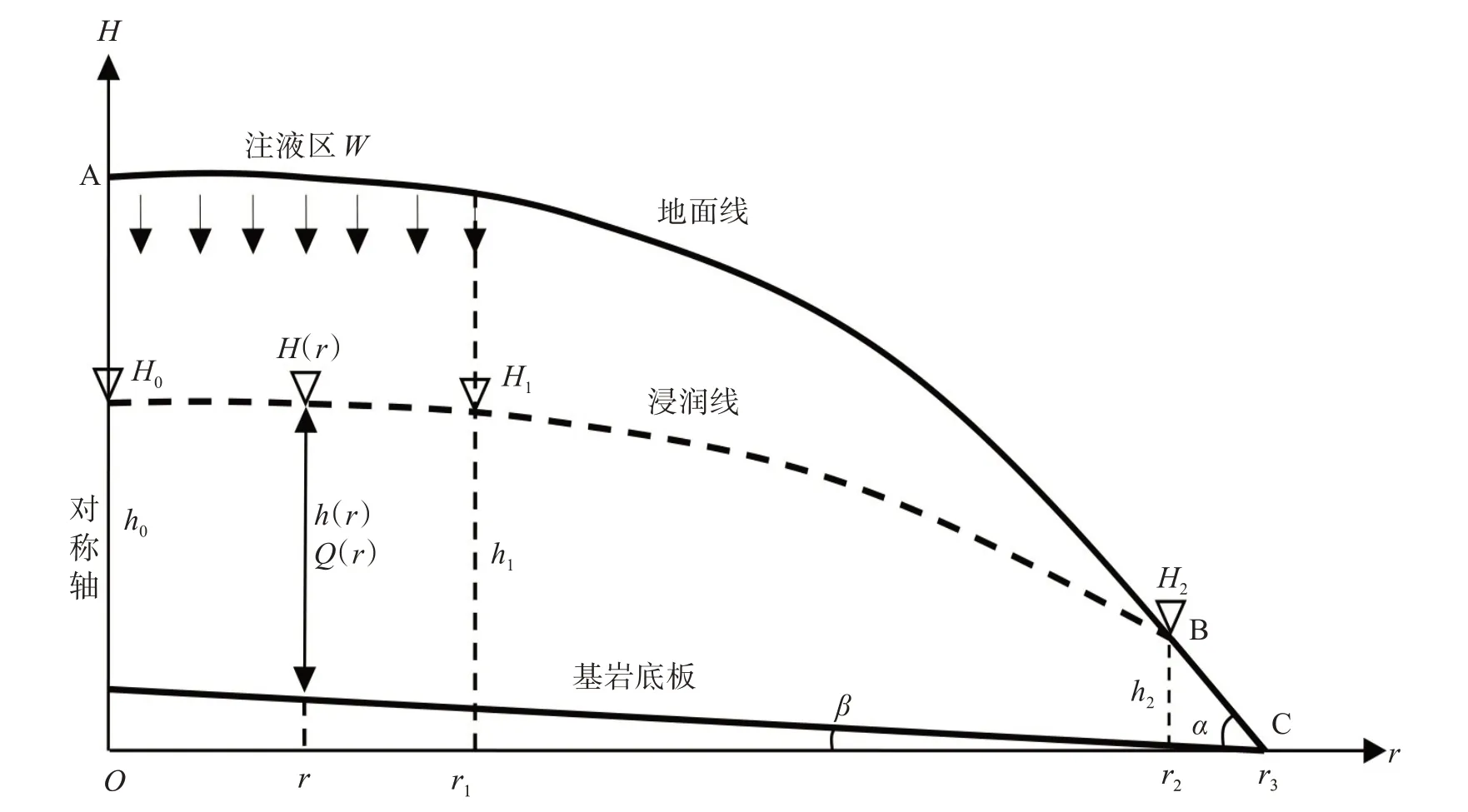
图3 浑圆形裸脚式矿山“注液-收液”轴对称简化模型Fig.3 The “liquid injection- liquid collection” simplified axisymmetric model of a rounded barefoot type mine
1)假设地表径流与地下径流分水岭在平面上重合处可作为中心轴线(r= 0),过中心轴线作垂直的H轴,取水平r轴与集液沟底板山脚出露点(图3中点C,坐标为r3,单位为m)相交,建立坐标系。
2)原地浸矿工艺要求集液沟能及时排除出渗母液,因此,可取点C为水头基准点(Hc= 0)。
3)基岩底板坡度一般较小,地形一般会有起伏,模型中简化为直线坡,按平均值β取值(单位:(°))。
4)修建集液沟时会挖除坡脚表层黏土直至矿层(见图1),因此,山坡出渗点B(坐标为r2,单位为m)处的坡度α(单位(°))一般较大。
5)图3 中地下水的运动分为2 个部分:①浸润线之上的注液区为非饱和渗流,属于土壤水分运动范畴,此处水流主要为在重力作用下的垂直向下渗流。单孔注液时,溶液从注液孔往周围非饱和矿体入渗,距离孔越远,矿体饱和度越低,湿润体的形状类似为椭球体[26-28];孔网注液时,由于孔与孔之间的相互影响,使得溶液在孔底以下一定范围外的非饱和矿体中的入渗变得均匀[25]。因此,图3 中注液区(注液范围为r1,单位为m)的边界条件简化为均匀的入渗强度W(单位水平面积、单位时间内入渗补给到地下水的水量,单位为m/d)。②浸润线之下基岩底板之上的区域为饱和渗流,属于地下水动力学范畴,此处水流主要为在重力、基岩坡度及液面比降作用下的水平流动。本文浸润线方程主要由第二部分水流在地下水动力学原理下进行推导,因此,当基岩底板坡度比较平缓、液面比降不太大的情况下,可以忽略垂向分流速而采用Dupuit假定。
6)随着注液的持续进行,矿体内部逐渐从基岩底板开始往上饱和,浸润线也越来越高,直至趋于稳定。一般情况下,原地浸矿生产周期6~8 个月,浸矿剂溶液在前40 天左右注完[4],而后注入上清液,此时矿体内的浸润线已接近于稳定浸润线(图3 中虚线所示)。因此,可以用稳定浸润线近似代替实际最高浸润线。
7)本文不考虑矿山土体渗透系数的空间变异性及各向同性。
1.2 稳定浸润线方程的推导
将图3 视为轴对称问题,即假设在环向没有水流,过水断面为以点O为圆心的圆柱面,水头线为上凸的曲线。分析图3的流线可知,水流有径向和垂向2个方向的分流速,属于轴对称二维流。若允许引进Dupuit 假定,忽略垂向分流速,则水流可简化为径向的一维流动计算[29]。
对于裸脚式稀土矿山,基岩底板一般从分水岭向集液坑方向(流线方向)呈顺坡倾斜(本文不考虑角度的正负值,取图3中α>β>0 °),当β<20 °时,渗流长度可以用径向距离来近似表示[29],水力坡度表示为-dH/dr。此时,H(r)=h(r)+tanβ·(r3-r),dH/dr=dh/dr-tanβ。依据水均衡原理,利用分段法,可得任意渗流断面处的总流量公式为:
式(1)中:Q(r)为任意渗流断面处的总流量数值,单位m3/d;W为注液入渗强度数值,单位m/d;r为任意渗流断面径向坐标数值,单位m;r1为注液范围数值,单位m;r2为出渗点B坐标数值,单位m。
根据Dupuit微分方程
式(2)中:β为基岩坡度数值,单位(°)。
对于注液区域(0≤r≤r1),可得
分离变量后,令λ=W/ks,作0→r的不定积分
由于H与r之间的函数关系未知,式(4)左边第三项无法积分,但可根据积分中值定理近似求解。令,rm介于0→r之间,由于浸润线方程光滑,可近似取rm=r/2。因此,得到倾斜底板注液区域(0≤r≤r1)稳定浸润线方程
对于非注液区域(r1≤r≤r2),可得
分离变量后,作r1→r的不定积分
由于浸润线在渗出点B处与下游坡面相切[30],即B点应该满足以下2个条件
式(9)、式(10)中:H2为出渗点B(r=r2)处水头数值,单位m;r3为C 点坐标数值,单位m;α为出渗点B 处的坡度数值,单位(°);JB为出渗点B处水力梯度。
将式(10)及点(r2,H2)代入式(8),并联合式(9),可得
由于H1>H2>0,定f1=tanβ·(2r3-r1-r2),将点(r2,H2)代入式(11),可得
由于H0>H1,定f2=tanβ·(2r3-r1),将点(r1,H1)代入式(6),可得
综合式(5)、式(8)—式(14)可得到倾斜底板稳定浸润线方程
式(15)为一般情况下矿山稳定浸润线方程,对于基岩底板水平的情况,令β= 0°,可将式(15)简化为
根据式(15),均匀稳定注液入渗(λ>0)的条件下,注液区的浸润线是椭圆线的上半支,非注液区的浸润线是抛物线与对数曲线组成的复杂形状。令式(15)中的λ= 0、r1=0(即不注液),可求得H0=H1=H2=tanβ·r3,过水断面高度h0=h1=h2=0,与实际情况相符。经验表明,当注液入渗量不足时,基岩面难以形成完整的浸润线。因此,如果得到完整的浸润线,应该满足条件H0≥tanβ·r3,将该条件代入式(15),即可求得给定注液范围下的最低注液强度或给定注液强度下的最小注液范围。
2 浸润线计算误差的参数分析
2.1 有限元模型与工况
为了进一步分析浸润线方程式(15)及式(16)的计算误差,根据矿山的地形条件和注液条件,提出4 个参数:出渗坡度(α)、基岩坡度(β)、注液范围和相对渗透系数(λ),按图3 简化模型建立有限元模型,将有限元计算结果作为对照值,分析上述4 个参数对浸润线方程计算误差的影响规律。其中,α可根据山脚集液沟设计和施工情况确定;β应根据矿山工程勘探资料给出的地质剖面图确定;r12/r32根据矿山注液方案中矿体分布情况确定,同时避开边坡坡度陡峭处;λ根据矿山注液方案和土体渗透系数ks确定,注液方案给出了矿山注液范围的面积A(单位:m2)和注液总强度Q(单位:m3/d),ks通过室内、外土体渗透性实验确定,则相对渗透系数λ=Q(/Aks)。
矿山建模高度为30 m,长度r3= 50 m,计算工况见表1。
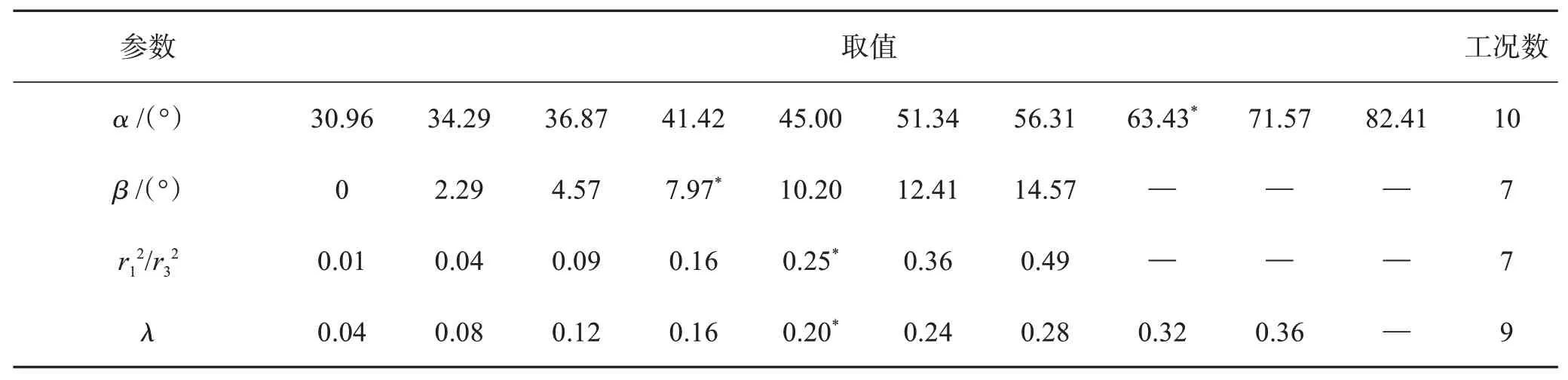
表1 计算工况汇总Table 1 Summary of calculation conditions
2.2 计算误差参数分析
典型工况(各参数均取基本值)下,浸润线对比分析如图4 所示。由图4 可知,方程计算浸润线基本位于数值计算浸润线之上,但两者非常接近,其计算误差沿流场方向逐渐增大,即注液段误差最小,中间段误差次之,出渗段(出渗点附近)误差最大;但在出渗点处,方程计算浸润线却位于数值计算浸润线之下。这是因为:本文浸润线方程的推导引入了Dupuit 假定,该假定在地下分水岭附近及出渗点附近并不满足[29],分水岭附近,垂向流速较大,铅垂面十分接近流面,不能假定为等水头面,Dupuit 假定忽略了垂向流速,因此,公式计算值一般要比实际值偏大;出渗段等水头面往往比较弯曲,水力梯度逐渐变大,以利地下水渗出成为地表水,并产生“水跃”现象,而Dupuit假定不能考虑“水跃”现象,且本文浸润线方程在出渗点处满足浸润线与出渗边坡相切的条件,造成浸润线在该处“弯曲”严重,因此,公式计算值一般要比实际值更小。

图4 典型工况下浸润线对比Fig.4 Comparison chart of steady seepage lines under typical working conditions
为进一步分析各参数对不同部位浸润线方程计算结果的影响,下面以分水岭(r= 0 m)、中间点(r12/r32= 0.5)与出渗点(r=r2)分别分析4个参数对浸润线方程计算误差的影响规律。
浸润线计算误差随出渗坡度的变化曲线如图5所示,由图5可知:浸润线计算值在分水岭及中间点较数值解偏大,且随出渗坡度的增大而小幅增大,误差最大值为11.42%;浸润线计算值在出渗点较数值解偏小,且误差的绝对值随出渗坡度的增大呈现先增大后减小的变化趋势,当出渗坡度α=41.42°时,误差最小值为-13.51%。由于修建集液沟时会挖除坡脚表层黏土,出渗坡度α一般较大,因此,出渗坡度α对浸润线计算误差较小。

图5 浸润线计算误差随出渗坡度的变化曲线Fig.5 The changing curve of calculation error with the seepage gradient
浸润线计算误差随基岩坡度的变化曲线如图6所示,由图6 可知:浸润线计算值在分水岭及中间点较数值解偏大,在出渗点较数值解偏小,且误差的绝对值随基岩坡度的增大近似线性增大,该误差的产生是由于本文浸润线方程中水力梯度的计算忽略了基岩坡度的影响,而采用水平距离近似表示渗流长度,因此基岩坡度越大,误差越大。由于原地浸矿基岩坡度一般较小(β<15°),因此,出渗坡度对浸润线计算误差的影响较小。

图6 浸润线计算误差随基岩坡度的变化曲线Fig.6 The changing curve of calculation error with the gradient of bed rock
浸润线计算误差随注液范围和相对渗透系数的变化曲线分别如图7 和图8 所示,由图7 和图8 可知:浸润线计算误差随注液范围和相对渗透系数具有类似的变化规律,即误差的绝对值随着注液范围或相对渗透系数的增大而减小。定义矿山相对注液强度Wr为矿山实际注液流量与矿山总面积下饱和注液流量之比,即Wr=λ·r12/r32,可知,图7和图8均反映的是浸润线方程计算误差随矿山相对注液强度Wr的变化规律,当相对注液强度Wr很小时,矿山基岩上甚至不能形成完整的浸润线,此时浸润线计算误差较大,这种情况只发生在原地浸矿注液初期;在注液稳定期,矿山相对注液强度Wr较大,矿山基岩上形成了较高的浸润线,浸润线方程计算误差较小。
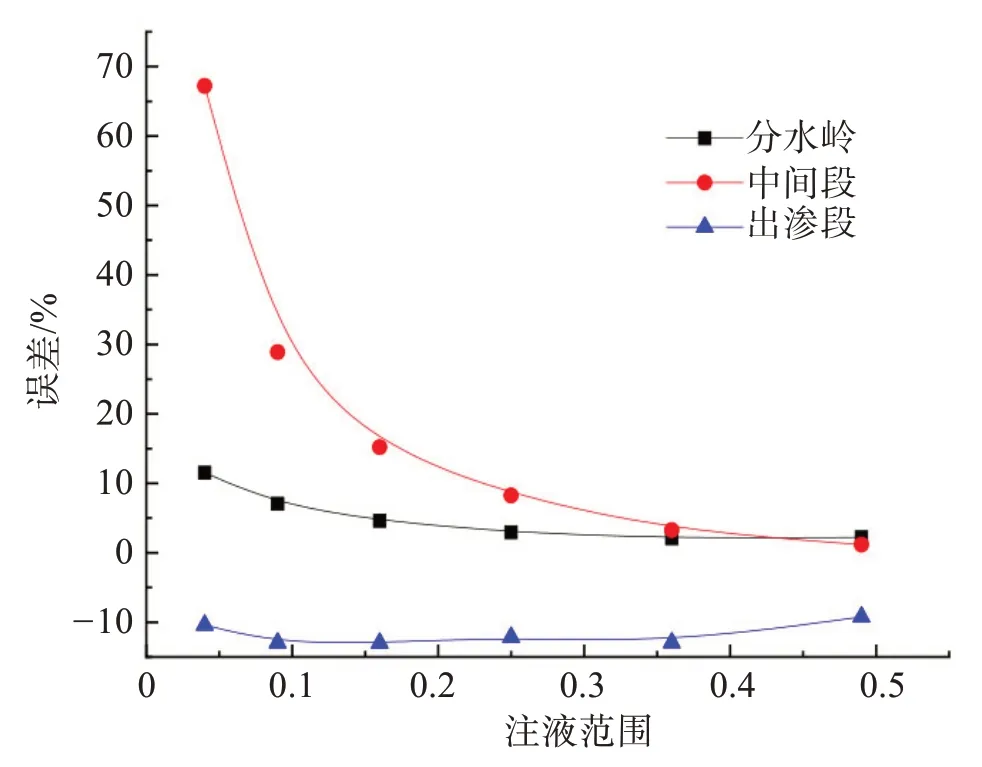
图7 浸润线计算误差随注液范围的变化曲线Fig.7 The changing curve of calculation error with the range of liquid injection

图8 浸润线计算误差随相对渗透系数的变化曲线Fig.8 The changing curve of calculation error with the relative permeability coefficient
3 结 论
1)选取浑圆形裸脚式稀土矿山为研究对象,建立原地浸矿“注液-收液”轴对称简化模型,基于地下水动力学和Dupuit 假定,推导得到矿山稳定浸润线方程,方程以分段函数表示,其中注液区的浸润线是椭圆线的上半支,非注液区的浸润线是抛物线与对数曲线组成的复杂形状。
2)以有限元计算结果为对照值,分析出渗坡度、基岩坡度、注液范围和相对渗透系数等参数对浸润线方程计算误差的影响,发现方程计算浸润线基本位于数值计算浸润线之上,但两者非常接近,其计算误差沿流场方向逐渐增大,但对于原地浸矿而言,各参数取值对方程计算误差的影响较小。
3)原地浸矿浸润线的高低与形状是矿山“注液-收液”渗流场形成与发展的结果,同时浸润线的高低与形状又跟矿山边坡稳定性、矿体浸泡体积百分比及资源浸取率等密切相关,因此浸润线方程可为原地浸矿“注液-收液”浸渗环节的“事先预测(设计)”提供理论依据。
4)浸润线方程的求解需要确定地形条件(α、β和r3)和注液条件(r1和λ),模型参数比较多,某些参数不易获取,且模型和参数均作了一定程度上的简化,计算结果应充分评估后使用。
