单元起始课教学要注意“虚实结合”

徐国红

摘  要：数学教学要重视单元起始课教学，给学生宏观的指引和整体的印象，将学生带进单元学习的大门。以《对称图形——圆》一章为例，说明单元起始课教学要注意“虚实结合”：帮助学生构建学习路径，窥探学习内容，了解“学什么”的顺序；引导学生明确核心概念，初探根本性质，体会“怎么学”的方法。

关键词：初中数学；单元起始课；《对称图形——圆》

《义务教育数学课程标准（2022年版）》确立了核心素养导向的课程目标，为此，强调教学内容的结构化。［1］因此，教师需要重视单元（包括教材编排的章节和教师根据内在的关联跨越教材章节整合的“知识块”）整体教学。对此，尤其要关注单元起始课教学，给学生宏观的指引和整体的印象，将学生带进单元学习的大门。在教学中，笔者体会到单元起始课教学要注意“虚实结合”。下面，以苏科版初中数学九年级上册第2章《对称图形——圆》为例来说明。

一、“虚”：构建学习路径，窥探学习内容，了解“学什么”的顺序

为了给学生宏观的指引和整体的印象，单元起始课教学要帮助学生构建单元学习路径（包括起源背景），窥探单元学习内容（包括相互关联），让学生了解“学什么”的顺序。这就是单元起始课教学的“虚”：不具体研究某个“知识点”。它可以让学生在后续的单元学习中有目标、有动力，也有助于学生初步体会单元学习的一般观念。

相比于小学数学课程，初中数学课程的安排进一步体现了近代数学发展基础的抽象结构思想：不仅要知道研究对象是什么，更重要的是知道研究对象的性质是什么、关系是什么、运算是如何开展的。［2］聚焦到“图形与几何”领域，研究对象除了主要作为图形要素存在的点、线、面、角之外，主要是几个基本的平面封闭图形，包括直边图形三角形（包括特殊的等腰三角形、直角三角形等）、四边形（包括特殊的平行四边形、梯形以及更特殊的矩形、菱形、正方形）和曲边图形圆。具体到“圆”这部分内容，小学阶段，学生从生活事物中抽象出圆这种图形，进而学会用圆规画圆，同时知道了圓心、半径、直径、扇形、弧、圆心角等相关概念，但是没有给圆下定义；然后，通过测量、归纳的方法认识了圆周率，知道了圆的周长公式；通过剪拼将圆转化为近似的平行四边形，借助极限思想，探索出圆的面积公式。

因此，《对称图形——圆》一章的起始课教学可以基于抽象结构思想，类比初中学习的三角形、四边形有关内容，顺承小学学习的圆的有关内容，引导学生构建学习路径，窥探学习内容。初中学习“圆”，首先要发现圆的本质特征，给圆下一个定义。其次要进一步研究圆的“性质”（包括“判定”，常表现为“关系”）。考虑到圆既是更为复杂的曲边图形，也和较为简单的直边图形有着丰富的联系。于是，既要研究圆和点的位置关系、圆之间的位置关系和大小关系、圆中弧的位置关系和大小关系，也要研究圆和直线的位置关系、圆中线段的大小关系、圆和角的位置关系、圆中角的大小关系，可能还要研究圆中弧、线段和角的关系，以及圆与三角形、四边形乃至多边形的关系，特别是研究其中的一些特殊情况（比如位置关系、大小关系的特殊情况以及与特殊的三角形、四边形乃至多边形的关系）。由此，学生不仅能初步了解本章“学什么”的顺序，而且能初步体会“先研究概念，再研究性质等，最后开展应用”和“从点、线、角等要素以及与其他图形关系的角度研究平面图形”等作为学习路径的一般观念。

二、“实”：明确核心概念，初探根本性质，体会“怎么学”的方法

单元起始课教学出于目标定位的考虑，受到课堂时间的限制，不太需要关注微观的学习方法和局部的学习内容。但是，如果只关注宏观的学习路径和整体的学习内容，则容易使课堂教学流于虚空。因此，还应重点关注单元基础的学习内容和贯穿的学习方法，引导学生在明确核心概念、初探根本性质的过程中体会“怎么学”的方法，从而更好地将学生带进单元学习的大门。这样，可以让学生在后续的单元学习中有抓手、有策略，同样有助于学生初步体会单元学习的一般观念。

显然，《对称图形——圆》一章的核心概念是圆。学生在小学学会了用圆规画圆。这时，圆的本质特征其实已经呼之欲出，只是考虑到小学生的抽象概括能力还比较弱，也缺乏用准确严谨的数学语言来表达的能力，所以暂时不让学生给圆下定义。到了初中，随着学生年龄的增长以及更具有抽象性和逻辑性的数学知识的学习和交流，在《对称图形——圆》一章的起始课中，教师可以引导学生回忆用圆规画圆的过程，抽象概括出圆的本质特征——圆上的点到圆心的距离等于半径，从而用准确严谨的数学语言给圆下一个定义。为了帮助学生更好地发现（理解）圆的本质特征，教师可以让学生同桌合作完成以下数学实验探究：（1） 一位同学在白纸上画一个半径为3 cm的圆，记作“⊙O”；（2） 另一位同学在⊙O所在的白纸上任意画3个点，记为“点A、点B、点C”；（3）两位同学共同判断所取的3个点与⊙O有怎样的位置关系，并思考判断的依据。在此基础上，教师可以引导学生进一步思考如何判断圆所在平面内任意一点和圆的位置关系——

师  （在黑板上画一个圆和一个明显在圆外的点）这个点和圆有什么位置关系？

生  在圆外面。

师  你是怎么知道的？

生  看到的。

师  很好！借助直观是研究图形的一个重要方法。（再画一个和圆贴得很紧的点）这个点和圆有什么位置关系？

生  感觉点在圆外。

生  不那么容易确定。

师  这说明我们的直观感知不够准确严谨，那么，我们怎么来判断点和圆的位置关系呢？或者说，我们怎么给圆下定义呢？

由此，教师便可以引导学生通过“到定点（圆心）的距离等于定长（半径）的点的集合”给圆下定义，通过点到圆心的距离与半径的关系判断点和圆的位置关系，并联系之前学习的三角形、四边形有关内容，进一步体会到“以数助形、定量刻画”“实验探索、逻辑推理”是研究平面图形的重要方法，也是一般观念。

结合苏科版教材的编写，不难发现，圆的根本性质是对称性，包括中心对称性（更一般地看，是旋转不变性）、轴对称性。在《对称图形——圆》一章的起始课中，教师可以给学生发放圆形纸片，让学生在圆周上任取两点，通过旋转使一点移动到另一点原来的位置，通过对折使两点重合，从而发现圆绕圆心旋转任意角度后都能和原来的图形重合，圆关于任意一条直径对称，即发现圆的旋转不变性和轴对称性。在此基礎上，通过增加点、连成线后旋转，初步感受“同一个圆中，相等的圆心角所对的弧相等，所对的弦也相等”的结论；通过连成线后的对折，初步感受“垂直于弦的直径平分弦，也平分弦所对的两条弧”和“平分不是直径的弦的直径垂直于弦，并平分弦所对的两条弧”的结论（垂径定理）——对这两个结论，只需要初步感受、大致表达，不需要严格证明、精确阐述。由此，教师便可以引导学生初步体会到“化曲为直”（化弧为弦、角）这种转化方法可能是研究圆（突破其“曲边”难点）的重要方法，也是一般观念。

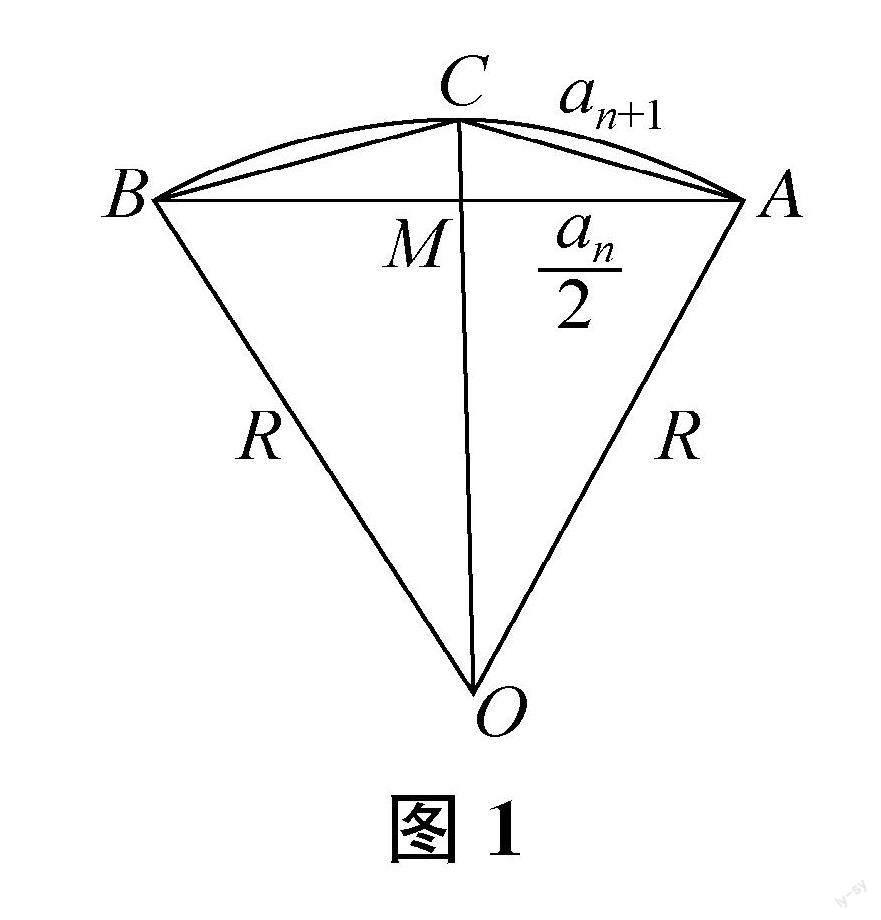
在此基础上，教师还可以引导学生思考：我们在小学是通过测量、归纳的方法实验得到圆的周长公式的，却通过“化曲为直”（将圆剪拼近似为平行四边形）的方法推导得到圆的面积公式，那么，也能通过“化曲为直”的方法推导得到圆的周长公式吗？对此，可能有学生在小学通过拓展阅读材料（如苏教版教材中的《你知道吗》栏目）初步了解我国古代数学家刘徽曾经采用的“割圆术”的求解思路：把圆周等分成若干段，近似看作线段求长度和，具体从六等分开始不断加倍，逐步逼近准确值。基于此，教师可以进一步介绍“割圆术”的求解关键：如图1，利用垂径定理和勾股定理，找到分加倍前后线段长度关系的递推公式。［3］

由此，学生可以进一步体会到“化曲为直”的转化方法常常和“无限逼近”的极限方法一起使用，从而不仅为本章后续学习“圆与正多边形”（理解其必要性）做好铺垫，而且为高中学习“球的表面积公式和体积公式”做好铺垫，乃至为高中或大学学习“定积分”做好铺垫；同时，初步体会到垂径定理处理圆问题的价值，以及递推方法（数学归纳法思想）处理无限问题的作用。

参考文献：

［1］中华人民共和国教育部.义务教育数学课程标准（2022年版）［S］.北京：北京师范大学出版社，2022：23.

［2］史宁中.数学课程标准修订与核心素养［J］.教育研究与评论，2022（5）：24.

［3］孙四周.还原祖冲之——我是如何在中学讲割圆术的［J］.教育研究与评论，2016（6）：6466.