一种螺旋桨飞机滑流影响的极曲线确定方法

商立英, 张超, 徐声明, 明亚丽, 杨诚

(中国航空工业集团公司第一飞机设计研究院, 西安 710089)

螺旋桨动力系统是当代亚音速飞机的主要动力系统之一,在较低亚音速的通用飞机、军用及民用运输机上获得了广泛应用[1]。在螺旋桨类飞机中,滑流对气动特性的影响是影响飞机飞行性能的重要因素。螺旋桨滑流的形成和发展过程比较复杂,且螺旋桨与飞机之间也存在一定的相互干扰,不同机型、动力装置下的滑流影响也有所差异,准确获得螺旋桨飞机在不同飞机阶段滑流影响下的升阻特性是螺旋桨飞机设计研究的热点和难点。

对于螺旋桨飞机的初步方案设计阶段,滑流对升阻特性的影响通常可以采用工程方法进行估算[2-4]。但是由于滑流形成和发展的过程比较复杂,不同机型、动力装置下的滑流影响差异也不同,这些方法难以准确预测不同拉力状态下影响量差异,仅局限于用于对设计方案的初步评估。

目前,中外学者对螺旋桨滑流的研究主要以计算流体力学(computational fluid dynamics,CFD)数值模拟和风洞试验为主。根据这些研究表明[5-12],螺旋桨滑流能够显著提高全机升力,但是同时也增加了阻力,产生“增升增阻”的效果,甚至会出现阻力的相对增量大于升力的相对增量的情况,导致全机升阻比减小;螺旋桨转速提高时,滑流强度越大, 对升、阻力系数的改变越大;滑流引起的升力系数增量、阻力系数增量随桨盘系数或拉力系数增加而增加,与拉力系数或桨盘系数成一定数值关系,但不同构型的飞机其比例关系差异很大。

根据以上研究结果,螺旋桨飞机在爬升、巡航、下降等各个飞行阶段由于发动机的功率状态不同,滑流的强度存在很大差异,因此在不同飞行阶段滑流对气动力的影响程度差异也很大,进而使飞机在巡航状态、和爬升状态下的极曲线存在很大差异,单纯使用某种飞行状态下的极曲线来计算评估不同飞行状态下的飞行性能,会导致计算结果出现较大偏差,甚至导致错误的评估结论。要获得准确性高的飞行性能评估结果,需要分别确定爬升、巡航、下降等典型飞行状态下的极曲线。

飞行试验是获取和修正飞机极曲线的重要手段。根据螺旋桨飞机不同飞行阶段气动力受滑流影响的特点,现通过在一般极曲线的表达式中引入拉力系数项,推导出一种同时适用于螺旋桨飞机巡航状态、爬升状态和下降状态的极曲线模型,简称通用极曲线,通过分析某型螺旋桨飞机的飞行试验数据确定出其通用极曲线的具体表达式,并将使用该模型计算得到的性能数据与试飞数据进行对比,验证其工程实用性。

1 螺旋桨飞机不同飞行状态极曲线

螺旋桨飞机滑流对飞机气动力的影响强弱可以拉力系数Tc来衡量[1],单台螺旋桨的拉力系数以机翼面积作为参考面积,即

(1)

(2)

式中:T为单台发动机拉力;q为动压;ρ为空气密度;v为速度;S为机翼参考面积。

采用上述定义方式后,Tc与飞机阻力系数参考面积一致,便于直接比较。图1为飞机在爬升、下降阶段时发动机相应工作状态下的拉力系数典型结果,飞机在巡航阶段的拉力系数介于爬升状态与下降状态之间。

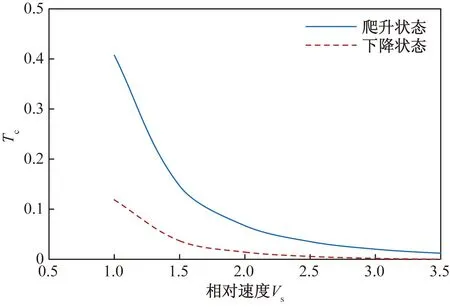
Vs为失速速度图1 不同飞行状态的拉力系数Fig.1 Tc at different flight phases

研究表明:螺旋桨滑流对气动力的影响随拉力增加而增大,与拉力系数存在一定的数值关系[1,11-14],螺旋桨飞机爬升时由于发动机处于大功率工作状态,滑流效应对全机气动特性影响非常明显,巡航状态发动机功率减小,滑流效应的影响相对减弱,滑流影响的气动力系数增量减小,下降状态发动机功率最小,此时滑流效应对全机的气动特性影响已经很微弱,气动力特性较无动力状态基本不变。当飞机飞行速度低于阻力发散速度时(对于螺旋桨运输类飞机来说这一条件通常是满足的),对于某一飞机构型,对应于不同的拉力系数,有不同的配平极曲线,通过CFD数值计算或风洞实验通常可以获得这样的一组极曲线,如图2所示。

在飞机的实际飞行中,上述的每条拉力系数为常值的配平极曲线上,只有一个点能够实现拉力与阻力平衡的等速平飞,把每条极曲线上的这种点找出来,连成一条新的极曲线,该极曲线即为飞机在这一构型下,稳定平飞配平极曲线[15],即巡航状态的配平极曲线。与稳定平飞状态所不同的是,飞机在航线爬升阶段发动机处于大功率状态,此时拉力大于飞机的阻力,滑流对升阻特性的影响较巡航状态大,而在航线下降阶段,通常发动机的功率状态很小(如空中慢车),此时拉力小于飞机的阻力,滑流对升阻特性的影响很小,此时的极曲线形态更接近于无动力状态下的极曲线,由此导致螺旋桨飞机在爬升、巡航、下降不同飞行状态下实际的配平极曲线是不同的,如图3所示。

图3 爬升、巡航、下降状态的极曲线形态Fig.3 Lift and drag polar at climb cruise and descent phases

2 滑流影响的极曲线模型

亚音速时,飞机在失速前的极曲线模型可以表示为

CD=CD,min+K(CL-CL0)2

(3)

式(3)中:CD为阻力系数;CL为升力系数;CD,min为最小阻力系数;CL0对应于CD,min的升力系数;K为诱导阻力因子。

由于螺旋桨飞机的极曲线直接与拉力系数Tc相关,为了得到同时适用于不同飞行阶段的极曲线,在式(3)中引入拉力系数项,以表征螺旋桨滑流对阻力系数的影响,即

CD=CD,min+K(CL-CL0)2+KTcTc

(4)

式(4)中:KTc为常数。

在飞机稳定平飞时,根据受力平衡方程,阻力[式(5)]等于拉力[式(6)],可得到式(7)。

D=qSCD

(5)

T=nqSTC

(6)

CD=nTc

(7)

式中:D为阻力;T为拉力;n为发动机台数。

将式(7)代入式(4)可得到

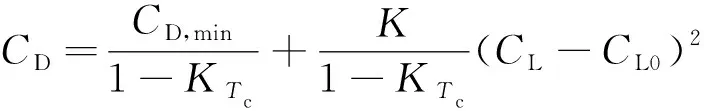
(8)

式(8)可以表达为

CD=CD,min_cruise+Kcruise(CL-CL0)2

(9)

式(9)中:

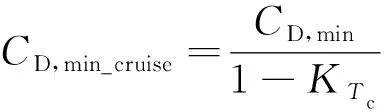
(10)

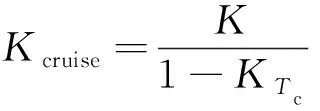
(11)

由此,式(9)即为螺旋桨飞机在巡航状态时的极曲线表达式。

根据以上关系,将式(10)和式(11)代入式(4),即得到同时适用于巡航状态、爬升状态、下降状态的配平极曲线表达式(12)。

CD=CD,min_cruise(1-KTc)+Kcruise(1-KTc)(CL-CL0)2+KTcTc

(12)

3 极曲线模型参数确定方法

3.1 飞机在垂直平面内的质心运动方程

飞机在垂直平面内,飞机的质心运动方程表达为

(13)

(14)

式中:γ为航迹角;α为迎角;φ为发动机安装角;P为推力(对于螺旋桨飞机该推力以拉力T的形式表示);m为质量;D为阻力;L为升力;W为重力;V为速度;t为时间。

根据式(13)和式(14),升力L和阻力D可表达为

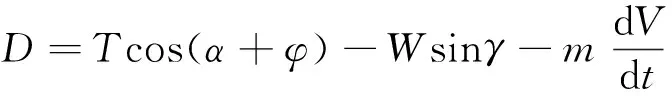
(15)

(16)

升阻力系数可表示为

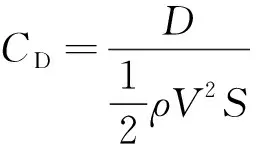
(17)

(18)

式中:CL为升力系数;CD为阻力系数。

3.2 拉力的确定

在对应的巡航、爬升、下降飞行试验中,测量飞行中扭矩、转速、总压和总温等参数,换算为飞行速度和高度。使用SAE-AIR-4065A[16]中的“J”方法,通过测得的扭矩和转速,得到轴功率,根据发动机厂商提供的功率特性和拉力系数特性得到,在轴功率特性图中,利用前进比和功率系数插值得到桨叶角,然后在拉力系数特性图中插值得到拉力系数,反算得到拉力值。

3.3 巡航状态极曲线参数确定方法

飞机巡航中以一定的速度稳定平飞时有

(19)

则式(15)和式(16)可简化为

D=Tcos(α+φ)

(20)

L=W-Tsin(α+φ)

(21)

通过飞机在巡航状态的稳定平飞飞行试验,测得飞机在不同的高度、重量、速度组合条件下稳定平飞时的发动机转速和扭矩,根据3.2节中的方法得到拉力数据,将拉力值与实时飞行重量W代入式(20)、式(21)、式(17)和式(18),可计算得到每一种高度、重量、速度组合下的升力系数CL和阻力系数CD的值代入式(9)即可以得到CD,min_cruise和Kcruise的值,由此确定出飞机在巡航状态下的极曲线表达式。

3.4 通用极曲线模型参数确定方法

飞机以一定的表速定常爬升、下降时可以认为航迹角变化很小,有

(22)

将式(22)代入式(16)可得

L=Wcosγ-Tsin(α+φ)

(23)

式(22)可以表达为

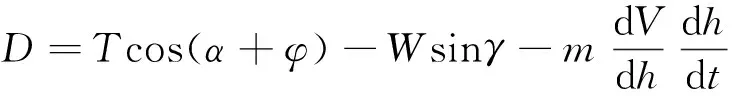
(24)

式(24)中:

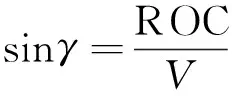
(25)

(26)

式中:ROC为爬升率(若为下降阶段则为下降率ROD);h为高度。

将式(25)和式(26)代入式(24)得到

(27)

式(28)可以表达为

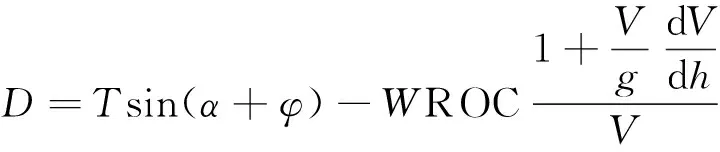
(28)

式(28)中:g为重力加速度。

由此阻力系数CD和升力系数CL由式(29)和式(30)计算。

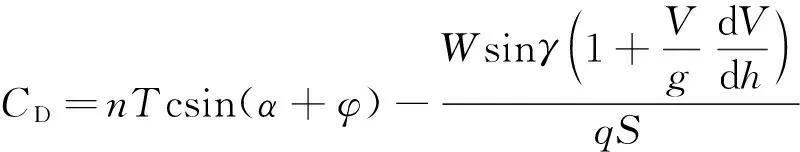
(29)

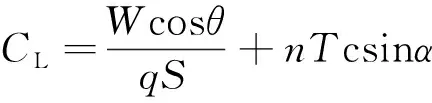
(30)

通过飞机以巡航构型进行定常爬升/下降试验,测得飞机在不同的高度、重量、爬升/下降速度组合条件下定常爬升/下降时各飞行参数的时间历程曲线,可以得到不同飞行条件组合下的爬升/下降率和dV/dh,测量相应状态下的扭矩和转速,使用3.2节中的方法得到拉力数据,将爬升/下降率、dV/dh和对应的拉力值与实时飞行重量W代入式(23)、式(28)、式(29)和式(30),可计算得到每一种高度、重量、速度组合下的升力系数CL和阻力系数CD的值,将每组CL与CD值和由3.3节中确定出的CD,min_cruise和Kcruise代入式(12),可确定出式(12)中的KTc,即可得到螺旋桨飞机在以相同构型在巡航、爬升、下降阶段的通用极曲线表达式。

4 某螺旋桨飞机极曲线参数的试飞确定

4.1 巡航状态极曲线参数

为了确定某螺旋桨飞机巡航状态极曲线表达式(9)中各参数的数据,将该飞机以巡航构型在不同重量、高度、速度的组合条件下进行稳定平飞飞行试验,根据3.3节中所述得到巡航状态的极曲线试飞值如图4所示,将试飞值使用最小二乘法进行拟合得到极曲线表达式(31),由式(31)中各参数的值可以确定式(9)中的巡航状态极曲线模型中的相关参数值见式(32)～式(34)。

图4 巡航状态极曲线试飞值Fig.4 Flight test value for lift and drag polar for cruise phase

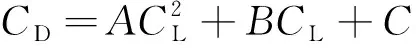
(31)

(32)

Kcruise=A

(33)

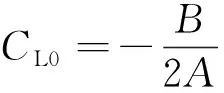
(34)

4.2 通用极曲线参数

发动机以最大功率状态,飞机在不同飞行重量、不同高度、速度下做锯齿爬升,根据式(23)、式(28)、式(29)和式(30)对爬升状态的试飞数据进行分析处理,得到爬升状态的升、阻力系数数据,将对应的升、阻力系数数据拟合成二次曲线如图5所示,使用图5中的极曲线结合式(31)得到式(12)中的参数KTc=0.23。将KTc和式(32)～式(34)的值代入式(12)即得到对于该螺旋桨飞机同时适用于巡航状态、爬升状态、下降状态的极曲线表达式(35)。

图5 爬升状态极曲线比较Fig.5 Comparison of lift and drag polar for climb phase between calculated data and flight test data

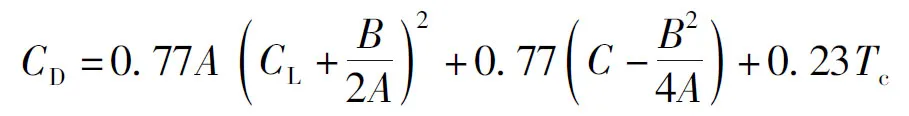
(35)

4.3 模型计算值与试飞值比较

将稳定平飞飞行试验中不同重量、高度、速度组合下的试飞点升力系数代入式(35)计算得到的阻力系数与试飞数据处理得到的阻力系数进行比较如图6所示,使用该模型得到的阻力系数与试飞得到的阻力系数的误差在5%以内。

图6 巡航状态阻力系数计算值与试飞值比较Fig.6 Comparison of drag coefficient for calculated data and flight test data

相同爬升条件下,使用该通用极曲线模型即式(35)计算的爬升率与试飞值的比较如图7所示,爬升率计算值与试飞值的误差较巡航状态偏大,个别点偏离了5%误差带。

图7 爬升率ROC计算值与试飞值比较Fig.7 Comparison of rate of climb (ROC) between calculated data and flight test data

相同下降条件下,使用该通用极曲线模型即式(35)计算的下降率与试飞值的比较如图8所示,下降率计算值与试飞值的误差基本在5%左右。

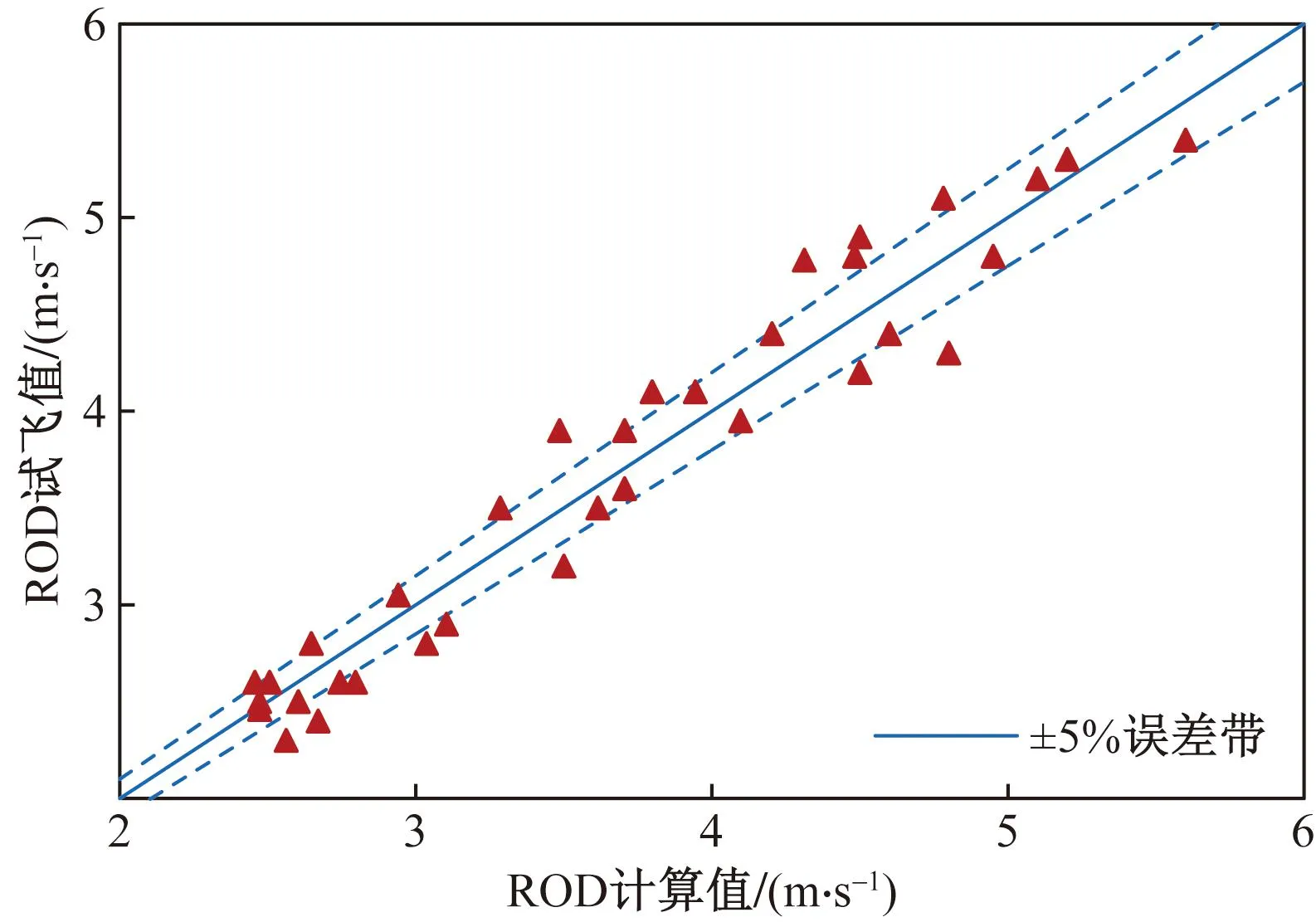
图8 下降率ROD计算值与试飞值比较Fig.8 Comparison of rate of descent(ROD) between calculated data and flight test data

5 结论

基于对亚音速飞机极曲线通用表达式的理论推导和假设给出了螺旋桨飞机爬升、巡航、下降状态的极曲线通用数学模型,通过一型螺旋桨飞机的稳定平飞和爬升性能飞行试验,得到了该极曲线模型中的各项系数,确定出适用于该飞机的通用极曲线表达式。

使用该螺旋桨飞机的通用极曲线对巡航阻力系数、爬升率和下降率进行计算,将计算结果与试飞值进行比较,得到如下结论。

(1)巡航状态的阻力系数与试飞值的误差基本在5%以内。

(2)下降状态下,使用该模型计算的下降率与试飞值的误差基本在5%左右。

(3)爬升状态下,使用该模型计算的爬升率与试飞值的误差较巡航状态、下降状态略大,绝大部分点在5%误差带以内,个别点偏离了5%误差带。

对于该螺旋桨飞机来说,使用该极曲线模型计算的飞行性能与试飞结果的误差在工程计算精度允许的范围,证明了该极曲线模型的工程实用性,可用于该飞机在不同飞行阶段的飞行性能扩展计算,同时为工程设计中确定螺旋桨飞机滑流影响下的极曲线提供参考。