采煤机永磁传动系统电机定子振动特性研究∗

姜 耸， 李 威， 盛连超， 王禹桥， 杨雪锋

（1.江苏大学机械工程学院 镇江，212013）

（2.中国矿业大学机电工程学院 徐州，221116）

（3.江苏师范大学机电工程学院 徐州，221116）

引 言

随着永磁技术的发展，低速大扭矩永磁同步电机驱动的齿轮传动系统越来越多地应用于重型机械装备中［1-2］。以采煤机永磁传动系统为例，由于低速大扭矩永磁电机的使用，采煤机截割部输入转速由3 000 r/min 下降为400 r/min。与三相异步电机相比，永磁同步电机具有调速范围宽的优点，并且由于去除了行星齿轮减速器，永磁传动系统具有较高的传动效率；但缩短传动链提高可靠性的同时，系统在受到外部波动剧烈的截割负载激励时，电机永磁体磁场与电枢磁场的叠加产生的强磁场将导致电机定子产生复杂的振动特性［3］。

研究人员发现，麦克斯韦电磁力是引起电机定子齿部振动的主要原因，并且对电磁力引起的永磁电机定子振动展开了广泛研究［4］。Wang 等［5］在所推导的永磁电机气隙磁通密度分布和径向力分布的基础上，对电机定子脉动模态和弯曲模态2 种振动特性进行了分析。Valavi 等［6］通过对开槽、半闭槽和磁楔3 种情况的比较，研究了槽谐波与电磁力之间的耦合关系。曹海翔等［7］定性分析了永磁直流电机定子振动规律，并与样机试验结果进行了对比。Lin 等［8］利用2 维 快 速 傅 里 叶 变 换 对 有 限 元 法 计 算的电磁力进行分解，并对电流谐波产生的电磁力展开了研究。

由于材料的磁致伸缩特性，当永磁电机功率逐渐增加时，定子磁致伸缩效应同样逐渐增强。由于降低了定子铁芯损耗的需要，非晶材料逐渐代替了传统硅钢材料。与传统硅钢相比，非晶合金的磁致伸缩系数大幅提高［9］。Belahcen 等［10］利用实验测试得到的材料磁致伸缩曲线对磁致伸缩力进行了研究。Xu 等［11］通过定子铁芯轭部和齿部的动力学模型，分析了定子铁心在不同半径、位置角和转子偏心下的磁致伸缩动态响应。吴胜男等［12］利用非晶合金材料磁致伸缩特性引起的永磁电机振动方程，对铁心振动位移、加速度等进行了研究。

上述对永磁电机定子振动特性的研究主要集中在中小型电机空载工况下，并未考虑外部工况与电枢磁场对定子振动的影响。笔者通过对永磁传动系统机电耦合动力学模型仿真，重点分析电磁力与磁致伸缩力引起的定子硅钢芯与非晶芯的振动特性，进一步对工作转速范围内定子共振点进行甄别。

1 采煤机永磁传动系统机电耦合动力学模型

在采煤机截割部中，永磁同步电机的输出扭矩与电机电阻、磁链等电气参数相关，齿轮传动系统的运动与齿轮质量、转动惯量等机械参数相关，这些电气参数与机械参数将相互耦合构成机电耦合系统，共同影响传动系统的运动。

1.1 永磁同步电机模型

采煤机永磁传动系统包括永磁同步电机、齿轮组、轴、轴承和截割滚筒等构件，永磁同步电机内部结构如图1 所示。其中：Rr为转子半径；Rm为永磁体半径；Rs与Ro分别为定子的内半径与外半径。

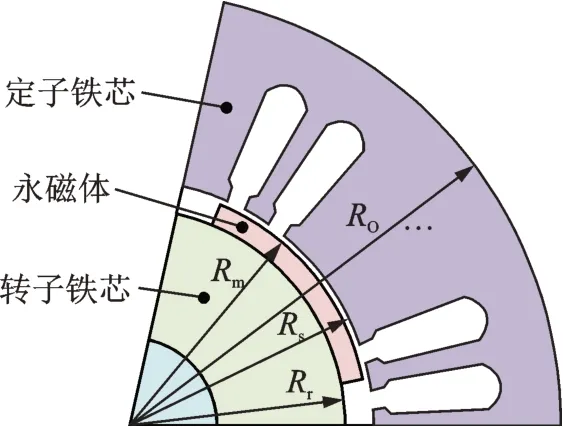
图1 永磁同步电机内部结构图Fig.1 Internal structure diagram of PMSM

气隙是磁场相互作用的场所，气隙磁通密度与永磁体、电枢及齿槽效应等因素相关。永磁体区域的磁场由准泊松方程控制，气隙与定子铁芯的磁场由拉普拉斯方程控制，这3个区域的控制方程可以表示为

其中：φm，φa，φs分别为永磁体、气隙、定子铁芯磁位；μ2为永磁体相对磁导率；M为永磁体剩余磁化矢量。

考虑相应的边界条件［13］，求解控制方程（1），可得定子无槽结构时永磁体产生的磁通密度为

其中：Brn（r），Bθn（r）分别为径向与切向磁通密度幅值，其详细表达式可参考文献［13］；p为磁极对数；θ为转子表面位置角。

笔者采用保角映射法，通过引入复合气隙磁导系数将无槽气隙转化为有槽气隙［14］，永磁体有槽气隙磁通密度为

其中：λa与λb为复合气隙磁导系数。

根据永磁体气隙磁通密度，永磁体产生的单相磁链可以表示为

其中：l为定子铁芯长度；γc为绕组节距角；Nc为单相线圈匝数。

由此可得dq坐标系下的永磁体磁链为

永磁同步电机的反电动势可通过对总磁链求导得到，最终电磁转矩可表示为

由于永磁电机在三相坐标系下的输入、状态和输出关系复杂，难以进行控制，因此笔者通过坐标变化，得到永磁同步电机dq坐标系的电压方程为

永磁电机控制方式采用转子磁链定向控制（i*d=0）和PI 控制的组合，其矢量控制模型见图2。图2 中转速环给出的q轴参考电流的表达式为

图2 永磁同步电机矢量控制模型Fig.2 The Vector control model of PMSM

其 中：Kpω，Kiω分 别 为 转 速 环PI 参 数；ω*m为 电 机 设定角速度；ωm为电机实际角速度；Ba为有功阻尼系数。

将q轴参考电流代入电流环，可得dq轴电压为

其中：Kpd，Kid，Kpq，Kiq分 别 为 电 流环PI 参 数；i*d为d轴电流设定参数。

将式（8）、式（9）代入式（7）中，可得电机电流为

1.2 齿轮传动系统模型

采煤机永磁传动系统如图3 所示，由3 级定轴齿轮与2 个惰轮组成。以第1 级减速齿轮为例，将时变啮合刚度展开成傅里叶级数，即

图3 采煤机永磁传动系统Fig.3 The permanent magnet transmission system of shearer

其中：kan为平均啮合刚度；kjan为谐 波幅值；j为 谐波级数；Z1为齿轮

1 的齿数；φ为啮合刚度的相位角。

齿轮副1，2 啮合时的传动误差可表示为

其中：R1，R2分别为齿轮副1，2 分度圆半径；y1，y2为对应轴承振动位移；et为齿轮副静态传递误差。

根据Lagrange-Maxwell 方程，齿轮副1，2 的平移-旋转动力学方程为

其中：k1，k2为轴承支撑刚度；c1，c2为轴承支撑阻尼；T1为齿轮1 输入扭矩；T2为齿轮2 负载扭矩。

相邻两级齿轮间受力通过轴传递，可将其转化为两质量旋转系统。以电机输出轴为例，有

其中：Ka为扭转刚度；Ca为扭转阻尼；Jm，J1分别为电机与齿轮1 转动惯量；Tm为电磁扭矩。

利用上述建模方式，建立各级齿轮组和传动轴的动力学方程

其中：X为广义坐标向量；M为广义质量矩阵；Tm，E，TL分别为电磁扭矩向量、误差激励向量和负载扭矩向量；Cn，Ct，Cr为对应阻尼矩阵。

1.3 截割滚筒负载模型

采煤机单个截齿受力如图4 所示，其中：h为瞬时切削厚度；bp为截齿工作部位宽度；lp为截齿截距；φ为切槽裂纹角。通过在基准截齿截煤时阻力的基础上，考虑实际截齿的几何形状与截割条件，对截割阻力加以修正［15］。

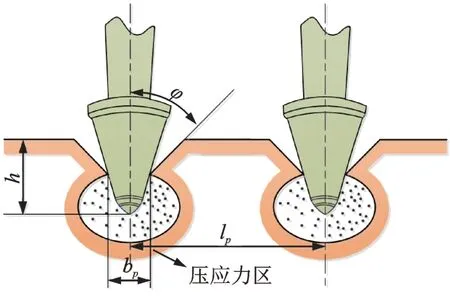
图4 采煤机单个截齿受力示意图Fig.4 Stress diagram of shearer single pick

滚筒上单个锐利截齿i的单位能耗为

其中：Z0为锐利截齿所受截割力；S0为截煤裂纹区域；煤层平均截割阻抗Ap=130f；煤岩坚固系数f=2.6。

截割滚筒的瞬时切削厚度h可以表示为

其中：vq为牵引速度；n为滚筒转速；m为滚筒截线截齿数。

切槽裂纹角与瞬时截割厚度及煤的脆性有关，即

其中：Kψ=2.1~3.5，为煤脆性影响系数。

根据能量守恒定律，单齿i在滚筒上的瞬时截割力可表示为

其中：K为综合考虑煤压张力情况、切削条件及刀具配置等因素的校正参数。

在截割不同煤层时，考虑了截割角度对截割力的影响。对于相同煤层形状的重复截割角，截割截面是恒定的，所以截割角对截割力的影响系数可以表示为

其中：Ky为截角影响系数；Kc为截齿排列系数；Kφ为前刀面形状系数；β为截齿偏转角。

截割滚筒处瞬时负载扭矩可以表示为

其中：D为滚筒直径；δcm为抗压强度；Sa为截齿投影面积；kδ为煤岩体积系数。

通过式（21）计算出所有截齿的截齿扭矩，然后对其进行叠加，得到截割负载扭矩。在机电耦合系统中，波动的截割负载与齿轮间的动态啮合力将传递到电机输出轴中，引起电机电流的变化，进而导致电机电磁扭矩的变化。永磁同步电机矢量控制引起的电磁扭矩的变化又会反过来影响齿轮传动系统。联立上述永磁电机、齿轮传动系统及截割负载扭矩模型，对其进行数值仿真，系统参数如表1 所示，可得额定工况下系统截割滚筒负载扭矩与电机A 相电流如图5 所示。滚筒截割扭矩中存在频率f1=0.76 Hz 和f2=1.5 Hz 的低频扰动，且该低频扰动通过齿轮传动系统作用在电机上，导致电源频率fm两侧出现以截割扭矩频率为间隔的边频带，可表示为fm±fi的形式。

表1 传动系统参数Tab.1 Transmission system parameters

图5 额定工况下系统截割滚筒负载扭矩与电机A 相电流Fig.5 Cutting drum torque and PMSM A phase current under rated condition

2 采煤机永磁传动系统电机定子应力计算

在以往研究中，小型永磁电机的磁致伸缩应力相较于麦克斯韦应力较小，一般忽略不计。但是，采煤机永磁传动系统中永磁电机具有低速、大功率特性，其定子磁场相较于小型永磁电机有较大增加，故电枢电流产生的磁通与磁致伸缩应力不可忽略。与此同时，由于降低定子铁芯损耗的需求，非晶材料逐渐代替了传统硅钢材料，由此产生的磁致伸缩应力更为显著。根据上述方法，电枢产生的气隙磁通密度［16］为

其中：Λ0为空气磁导；Nc为每相串联绕组匝数；βo，βs分别为齿槽开口角度和槽距角。

有载气隙磁通密度由永磁体与电枢磁通密度组成

为验证本研究永磁体磁场与电枢磁场在气隙内磁通密度解析方法的正确性，将式（23）在r=（Rm+Rs）/2 处的计算结果与ANSYS 21.1 实现的有限元分析进行了比较，该点在气隙中点，具有代表性。永磁电机的有限元磁场仿真如图6 所示。图7 为永磁电机在r=（Rm+Rs）/2 处永磁体与电枢径向磁通密度对比，由图可见，永磁体与电枢无槽定子铁芯径向磁通密度曲线是光滑的，但有槽定子铁芯的曲线存在一定的畸变。电枢电流径向磁通密度为0.419 T，达到永磁体径向磁通密度最大值1.165 T 的35.97%，因此电枢电流对磁通密度的影响同样不可忽略。总体上，解析分析结果与有限元分析结果吻合较好。

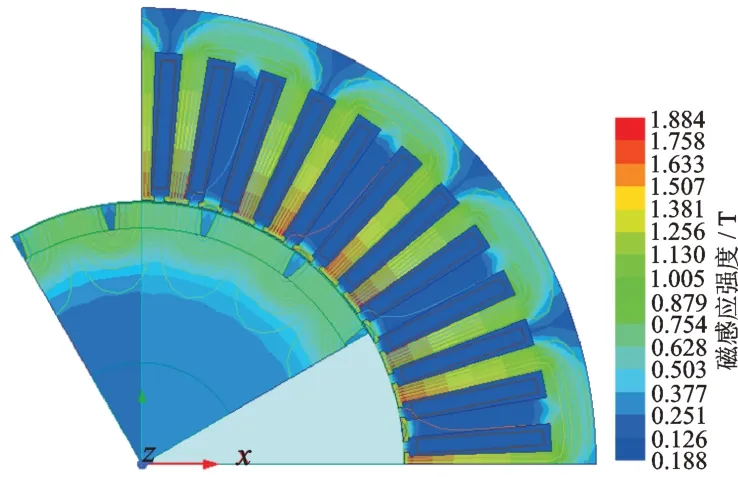
图6 永磁电机的有限元磁场仿真Fig.6 Finite element magnetic field simulation of PMSM

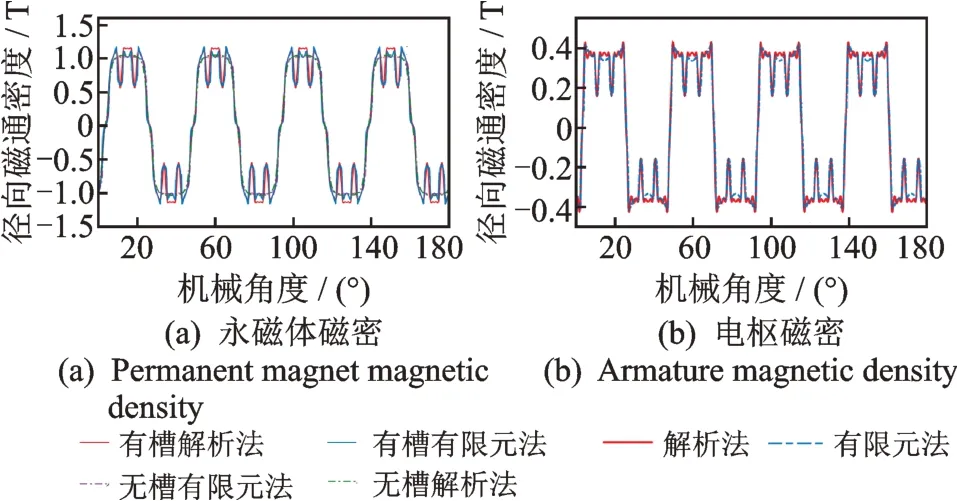
图7 永磁电机在r =(Rm+Rs)/2 处永磁体与电枢径向磁通密度对比Fig.7 Comparison of radial flux density between stator surface permanent magnet and armature at r =(Rm+Rs)/2

磁场作用在定子铁芯齿部上的麦克斯韦径向与切向电磁力为

定子铁芯可以在磁场中产生磁致伸缩应变，根据胡克定律，磁致伸缩应力可表示为

其中：E为 定子铁芯弹 性模量；α为泊 松 比；εr，εθ，εrθ分别为径向应变、切向应变与剪切应变。

定子铁芯常用硅钢材料DW465-50 与非晶合金材料2605SA1，其磁致伸缩特性如图8 所示。磁致伸缩应变ε随磁通密度非线性增加，且同等磁通密度下，非晶合金磁致伸缩应变相较于硅钢大幅增加。应变与磁通密度的关系可以表示为

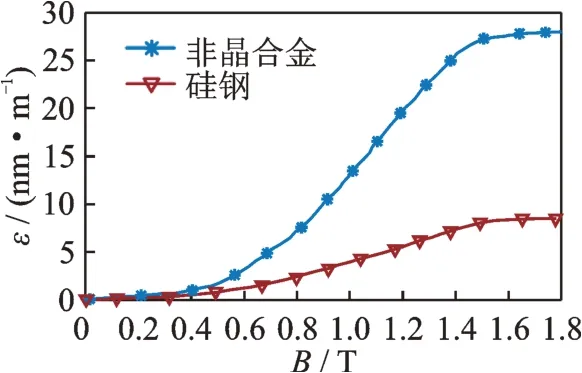
图8 非晶合金2605SA1 与硅钢DW465-50 磁致伸缩特性Fig.8 Magnetostrictive properties of amorphous alloy 2605SA1 and silicon steel DW465-50

其中：+，—分别表示定子铁芯内、外表面。

永磁电机中电机定子切向应力远小于径向应力，且电磁力主要作用在定子齿表面，定子振动主要为齿部沿径向方向振动，因此这里主要分析定子齿部径向应力分布与振动特性。通过对图8 磁致伸缩应变插值，并将式（26）代入式（24）、式（25），分别得到定子铁芯齿部径向电磁力与非晶合金、硅钢磁致伸缩应力特性，如图9 所示。麦克斯韦电磁力、磁致伸缩力均随机械角度周期性地变化，并含有多种频率成分，变化频率一致且均为电源频率的偶数倍。硅钢的磁致伸缩力最大值达到电磁力的23.8%，而非晶合金的磁致伸缩力相较于硅钢明显增加，其最大值达到电磁力的58.5%。

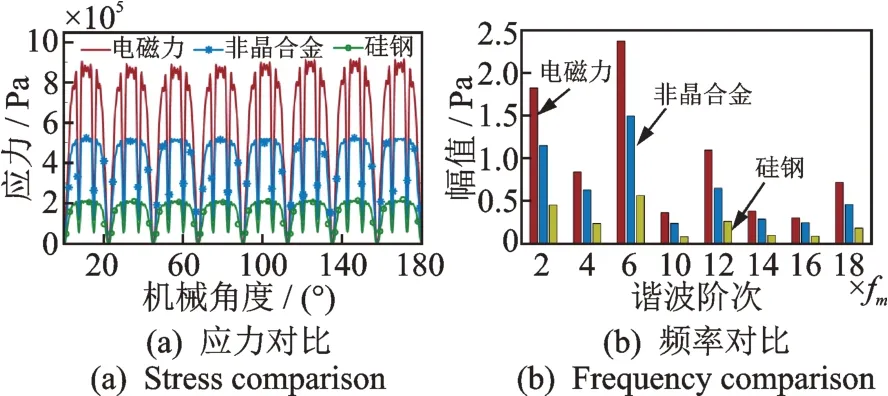
图9 定子铁芯齿部径向电磁力与非晶合金、硅钢磁致伸缩应力特性Fig.9 Radial electromagnetic force and magnetostrictive stress of stator core

3 永磁传动系统电机定子振动特性

3.1 定子振动模型

系统的受迫振动与系统质量、固有频率及阻尼等参数相关，为分析永磁电机定子的振动特性，需得到定子的固有频率fn。有限元法可较精准地得到定子固有频率，这里通过有限元对定子固有频率进行计算。定子铁芯有限元模型如图10 所示。为了与实际工况匹配，定子支撑方式选择两端固定支撑，因此定子模态振型以径向为主，其中定子铁芯齿部固有频率如表2 所示。

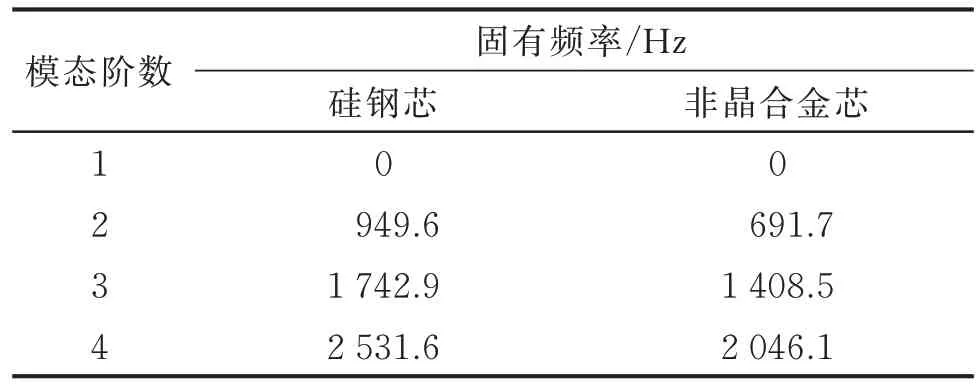
表2 定子铁芯齿部固有频率Tab.2 Natural frequency of stator core teeth

图10 定子铁芯有限元模型Fig.10 Finite element model of stator core

对于电机定子齿部上某一微元，其质量与阻尼可表示为

其中：ρ为材料密度；ξn为n阶模态所对应的阻尼比。

定子齿部各点电磁力与磁致伸缩力各不相同，这里以微元为单位进而得到各点振动位移。由表2可以看出，非晶芯各阶固有频率均小于硅钢芯，低阶的2 阶模态小于1 000 Hz，容易在电磁力与磁致伸缩力的诱导下产生共振现象，是研究电机定子齿部径向振动需要重点关注的模态，故这里主要研究由2 阶模态引起的振动特性。

定子齿部2 阶径向受迫振动方程可定义为

将式（24）、式（25）代入式（28），仿真得到定子铁芯齿部径向振动，如图11 所示。在额定工况下，电磁力与磁致伸缩力对径向振动位移有明显影响。径向电磁力单独作用时，振动位移达到了42.23 μm。定子为硅钢芯的磁致伸缩力单独作用时，最大振动位移为10.49 μm，达到电磁力单独作用时振动位移的24.84%；定子为非晶合金芯的磁致伸缩力单独作用时，振动最大位移为26.99 μm，达到电磁力单独作用时振动的63.91%；硅钢芯与非晶合金芯磁致伸缩力引起的振动位移所占电磁力引起的振动位移比例，均稍大于硅钢芯与非晶合金芯磁致伸缩力所占电磁力的比例23.8% 与58.5%。图12 为永磁体剩磁强度变化时的硅钢芯径向振动，硅钢电机定子齿振动位移随永磁体剩磁的增加而逐渐 增 加，由1.0 T 时 的15.52 μm 增 加 到1.5 T 时 的27.47 μm，故永磁体剩磁强度的增加在提高永磁电机功率的同时将加剧定子的振动。振动位移频谱组成与径向力、磁致伸缩力的频谱组成基本相同，但分布 不 同。振动 位 移 主 要 以2fm，6fm，10fm及18fm频率为主，其中18fm频率幅值明显增加，这主要是因为额定转速下，18fm靠近硅钢2 阶固有频率所致。

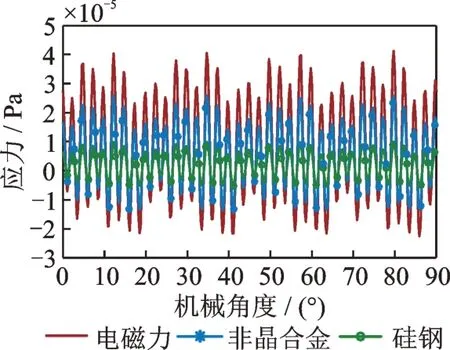
图11 定子铁芯齿部径向振动Fig.11 Radial vibration of stator core teeth

图12 永磁体剩磁强度变化时的硅钢芯径向振动Fig.12 Radial vibration of silicon steel core when remanence permanent magnet intensity changes

3.2 定子共振特性分析

永磁电机电磁力与磁致伸缩力中存在多种电源频率的倍频，在某些工况下，可能导致定子上产生共振现象，加剧定子振动，降低电机寿命。

采煤机永磁截割传动系统永磁同步电机的工作转速为264~440 r/min，根据定子的固有频率及各激励频率，绘制出永磁电机定子激励在工作转速范围内的坎贝尔图，如图13 所示。因高阶频率影响较小，故图中只展示了0~1 000 Hz 频率范围，其中fNS2与fNF2分别为硅钢与非晶合金的2 阶固有频率，固有频率与激励频率相同时即满足共振条件。由图13可知：当定子为硅钢时，系统在电机转速为393 r/min（A处）存在共振点；当定子为非晶合金时，定子齿在电机转速为288 r/min（B处）、324 r/min（C处）、371 r/min（D处）和433 r/min（E处）处均存在共振点。为了研究潜在共振点对采煤机永磁电机定子振动的具体影响，对系统进行升速仿真，使电机转速从264 r/min 匀加速升至440 r/min。

图13 永磁电机定子激励在工作转速范围内的坎贝尔图Fig.13 Campbell diagram of PMSM stator excitation in working speed range

通过对定子为硅钢时系统进行3 维阶次扫频分析，得到其在工作转速范围内的振动响应，如图14所示，电磁力与磁致伸缩力的激励频率线在图中清晰可见。在时域图中，电机转速为393 r/min 时，振动幅值明显增大，并且电机在额定转速400 r/min时，仍然在A点共振影响范围内。为分析共振点A对额定转速的影响，进一步研究420 r/min 处与400 r/min 处的振动响应，如图15 所示。转速为420 r/min 时，振动幅度较小，含有多种频率成分，以2fm，6fm及18fm等频率为主，共振激励频率18fm所占比例较小；转速为400 r/min 时，振动幅值与共振激励频率18fm所占比例明显增大。因此，定子在电机转速为393 r/min 时满足共振要求，并且对额定转速下的振动有较大影响。

图14 定子为硅钢时在工作转速范围内的振动响应Fig.14 Vibration response of silicon steel stator in working speed range

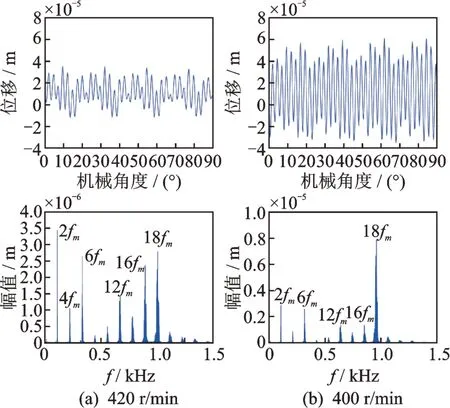
图15 定子为硅钢时的振动响应Fig.15 Vibration response with silicon steel

通过对非晶合金时的系统进行3 维阶次扫频分析，得到其在工作转速范围内的振动响应，如图16所示。从时域图中可以看出，振动位移振幅在324 r/min（C处）与371 r/min（D处）有所增大，但两者均没有出现明显突变，并且振动位移振幅在288 r/min（B处）与433 r/min（E处）明显增大，出现突变现象。进一步对转速为288 r/min（B处）与433 r/min（E处）进行仿真，其振动响应如图17 所示。在时域图中，两者的振动位移均较大，并且在D点的振动幅值大于B点；在频域图中，额定转速为288 r/min 时以激励频率12fm为主，其他频率所占比例较小，而在D点时，12fm对应的幅值占据主导地位，故非晶合金定子在288 r/min 与433 r/min 时均存在共振风险，并且电机在额定转速时不在两者共振影响范围内。

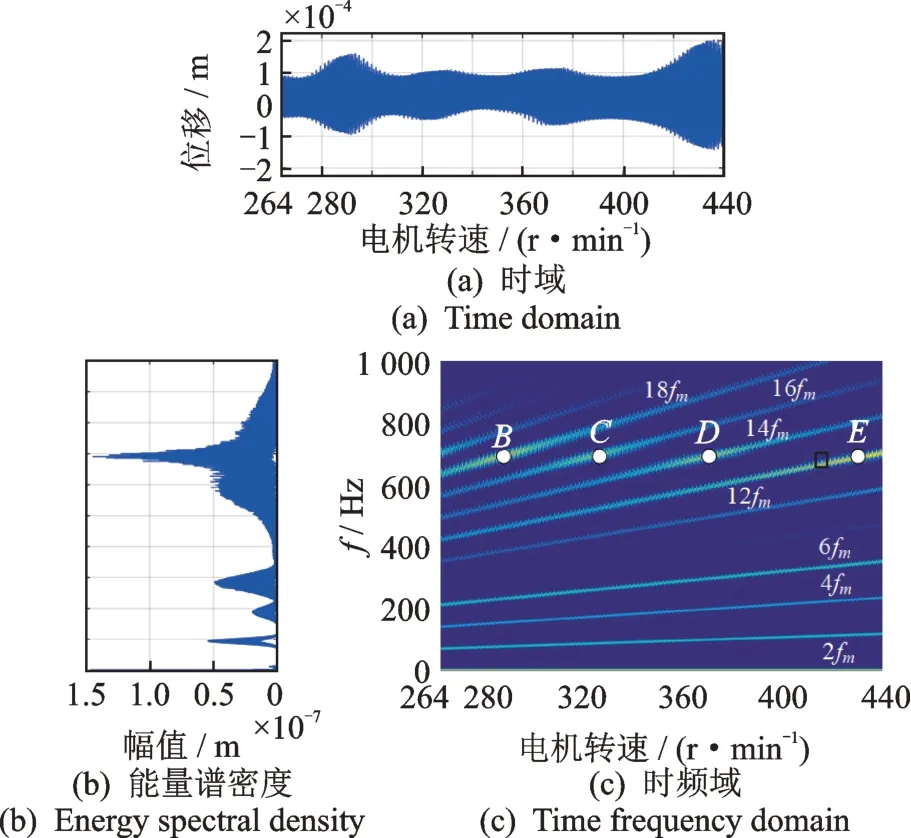
图16 定子为非晶合金时在工作转速范围内的振动响应Fig.16 Vibration response of stator made of amorphous alloy in working speed range

图17 定子为非晶合金时的振动响应Fig.17 Vibration response of amorphous alloy

4 结 论

1） 永磁同步电机中由于矢量控制方法的应用，电机转速与电流可实时调节，实现智能驱动。麦克斯韦电磁力、磁致伸缩力均随机械角度周期性变化，并含有多种频率成分，且均为电源频率的偶数倍。硅钢芯的磁致伸缩力最大值达到电磁力的23.8%，而非晶合金芯的磁致伸缩力相较于硅钢芯明显增加，其最大值达到电磁力的58.5%。

2） 硅钢芯与非晶合金芯磁致伸缩力作用下，定子齿振动位移达到电磁力作用时振动位移的24.84%与63.91%，两者磁致伸缩力引起的振动位移所占电磁力引起的振动位移比例均稍大于硅钢芯与非晶合金芯。永磁体剩磁强度增加，在提高永磁电机功率的同时将加剧定子的振动，定子振动位移频谱组成与径向力、磁致伸缩力的频谱组成基本相同，主要以2fm，6fm，10fm和18fm频率为主。

3） 定子为硅钢芯时，在电机转速为393 r/min时出现激励频率18fm引起的共振现象，且在电机额定转速时，仍然在共振点的影响范围内。定子为非晶合金芯时，在288 r/min 和433 r/min 时振动幅值出现突变，激励频率18fm和12fm分别占据主导地位，出现明显的共振现象；但在电机额定转速时，系统不在共振点的影响范围内。