恒磁通磁轴承轴向电感位移传感器参数研究∗

王纯一， 徐 旸， 张 剀

（清华大学工程物理系 北京，100084）

引 言

磁轴承是一种依托电磁力使转子悬浮在规定位置从而减小摩擦力的新型轴承系统。相比于传统的机械轴承，磁轴承具有无接触、无磨损、无需润滑以及转速高等特点［1-3］，广泛应用于压缩机、涡轮分子泵、透平机械和医疗器械等领域［4-8］。为使转子稳定悬浮，需要传感器实时检测转子位置信息。电感传感器是目前磁轴承常用的位移传感器之一，具有结构简单、制作成本较低、线性度好、灵敏度高及不易受外界低频噪声干扰等优点［9-13］。但是，由于传感器探头和传感器目标材料磁化曲线的非线性，当外磁场发生变化时，相对磁导率将会发生变化，进而导致电感变化，所以电感传感器在外磁场变化时将出现工作点漂移的问题。

文献［14-15］提出了一种恒磁通轴向电感位移传感器，当激励电压恒定时，该传感器产生的激励磁通恒定，与外磁场无关，通过检测传感器感生线圈中感生电动势随转子位移的变化，获取转子轴向位置信息。该传感器可有效抵抗外磁场的干扰，但是灵敏度较低。相关文献仅给出了传感器的原理及结构，未对灵敏度与传感器参数的关系进行分析。传感器参数包括机械参数和电气参数两部分。机械参数主要为传感器探头和传感器目标间的气隙大小，将影响传感器的漏磁大小，进而影响传感器感生线圈的感生电动势，最终影响传感器的灵敏度。电气参数包括激励电压、激励频率、传感器功率及激励线圈匝数等，会影响激励磁通的大小，进而影响传感器感生线圈的感生电动势，最终影响传感器的灵敏度。在该传感器实际应用时，通常使用功率放大器驱动激励线圈，由于功率放大器的驱动能力有限，因此传感器设计的关键是如何设计传感器的各项参数，使其在功放驱动能力范围内达到尽量高的灵敏度。

笔者着重研究传感器探头参数对灵敏度的影响，不对检测电路部分进行研究，因此暂未讨论精度、带宽等指标。首先，推导得到灵敏度与气隙距离近似呈反比，并通过仿真和实验进行了验证；其次，推导了感生电动势与电气参数的关系式，根据功率放大器的输出限制参数和涡流效应的限制，确定了视在功率和激励频率为决定传感器灵敏度的电气参数；最后，给出了在功放输出范围内最大化传感器灵敏度的参数设计方案。

1 恒磁通轴向位移传感器工作原理

为解决测量受外磁场影响的问题，提出了一种新型恒磁通轴向电感位移传感器［14-15］，该传感器激励线圈产生的磁通量恒定。笔者发现，通过对其拓扑结构进行改进，可提升传感器灵敏度。改进后的恒磁通电感传感器轴向剖面图如图1 所示。

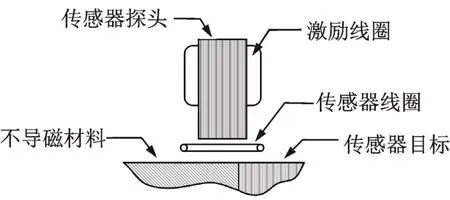
图1 恒磁通电感传感器轴向剖面图Fig.1 Axial section of inductive sensor with constant flux

转子左侧为不导磁材料，右侧为导磁的传感器目标，为减少涡流效应的影响，通常使用硅钢片堆叠而成。该传感器在传统的电感传感器探头与传感器目标之间加入了一个传感器感应线圈（以下简称传感器线圈），通过测量传感器线圈的感生电动势获取转子轴向位移。恒磁通电感传感器径向剖面图如图2 所示，转子运动方向垂直于纸面。

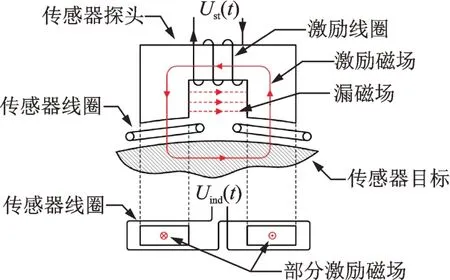
图2 恒磁通电感传感器径向剖面图Fig.2 Radial section of inductive sensor with constant flux

激励线圈上施加幅值频率恒定的正弦激励电压Ust，产生交变的激励磁场。传感器线圈产生的感应电压为Uind。传感器线圈在左右两个磁极处的绕线方向相反，这样不仅使激励磁场（通过两检测线圈的磁通方向相反）产生的感生电动势同向叠加，又使外部干扰磁场（通过两检测线圈的磁通方向相同）在传感器线圈上产生的总感应电动势为0。

根据电感两端电压与电流的关系及电感的定义，可得由激励电压产生的激励磁通量Φ为

其中：N为绕线匝数；u为激励电压。

激励磁通量仅与绕线匝数和激励电压有关，与外磁场无关，所以当激励电压恒定时，产生的激励磁通量也恒定。即使外磁场导致相对磁导率μr改变，激励磁通量也不会改变，因此该传感器对外磁场的抵抗能力较强。

当转子轴向运动使传感器探头与传感器目标间的重叠面积减小、磁阻增大时，图2 中虚线所示的两磁极间的漏磁场增大，因此穿过传感器线圈的激励磁通量减小，传感器输出的感生电动势减小。该传感器基于产生的激励磁通恒定，利用漏磁场随转子轴向位移的变化，通过测量传感器线圈中感生电动势的变化获取转子轴向位移。恒磁通传感器大致测量范围如图3 所示。

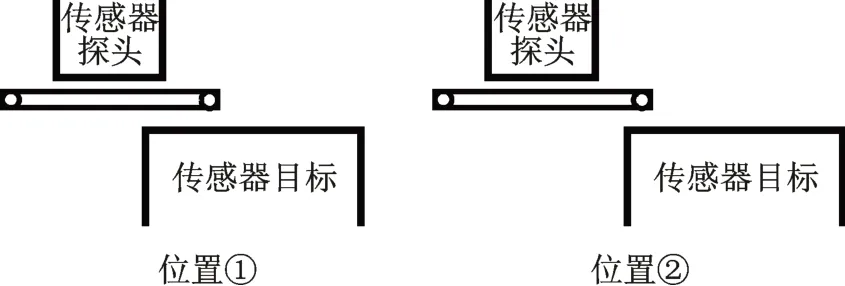
图3 恒磁通传感器大致测量范围Fig.3 Approximate measurement range of new sensor topology

2 机械参数对传感器灵敏度的影响

2.1 理论推导

根据图2 所示的磁路，该传感器的等效磁路如图4 所示。其中：N为激励线圈匝数；i为激励线圈上的电流；Φ为总激励磁通。

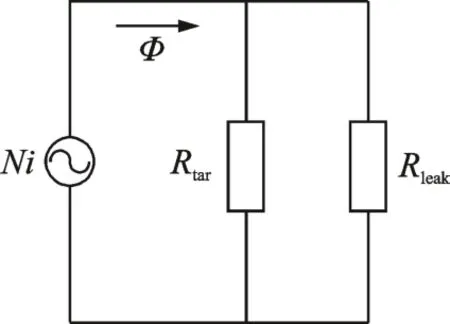
图4 图2 的等效磁路Fig.4 Equivalent magnetic circuit of figure 2

Rtar为经过气隙和传感器目标磁路的磁阻，Rleak为漏磁场磁路的磁阻。由于传感器探头和传感器目标的磁导率很大，与空气相比其磁阻可以忽略。当忽略传感器目标左侧面的漏磁时，有

其中：Rgap为气隙的磁阻；δ为气隙大小；μ0为空气的磁导率；A为传感器探头和传感器目标的重叠面积。

Rleak仅与传感器探头两磁极间面积和距离相关，因此为定值。Rtar所在磁路的磁通量即为通过传感器线圈的磁通量，有

传感器的灵敏度Ssen为转子轴向移动单位距离导致的感生电动势变化，轴向移动距离正比于重叠面积A，感生电动势正比于通过传感器线圈的磁通量，因此有

故

由式（5）可知，为提升传感器灵敏度，需要减小重叠面积A，故平衡位置处于图3 中位置①附近。由于A很小，则式（5）分母中的μ0RleakA很小，可以忽略，于是在工程应用的气隙大小范围内近似有

因此，气隙越小则灵敏度越高。

2.2 仿真结果

对该传感器进行三维有限元电磁场仿真分析。为便于安装，传感器探头选用了集成式的结构，将4个传感器探头（1 个传感器探头包含2 个磁极）集成到1 个定子盘上。集成式定子盘模型如图5 所示，其参数见表1。传感器感应线圈模型如图6 所示，大小为6 mm×12 mm。 组装后的仿真模型如图7所示。

表1 集成式定子盘参数Tab.1 Parameters of integrated stator disk

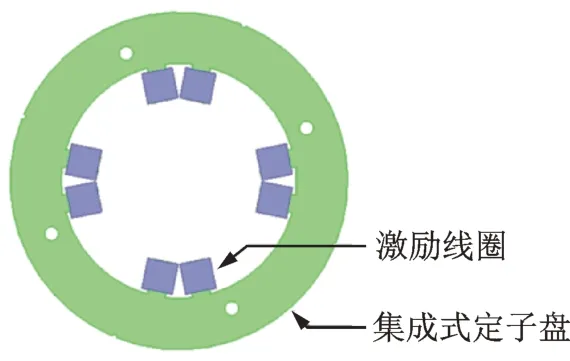
图5 集成式定子盘模型Fig.5 Model of integrated stator disk

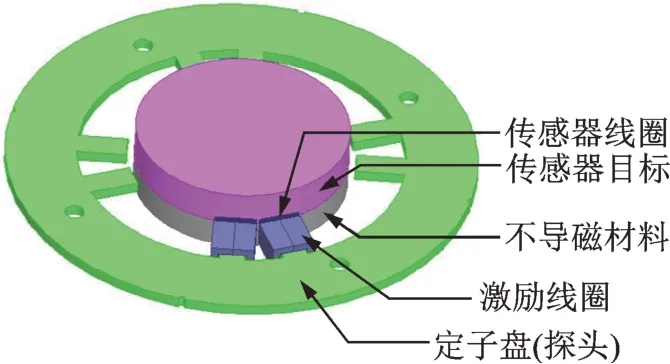
图7 组装后的仿真模型Fig.7 Assembled simulation mode

基于定子盘的对称性，为加快仿真速度，仅对1个传感器探头的2 个磁极（线圈绕线方向相反）并联施加40 kHz、幅值为15 V 的正弦激励电压。仿真传感器目标初始位置（即轴向位移为0 处）如图8 所示，向右为轴向位移的正方向。维持激励线圈电压频率和幅值恒定，通过改变转子直径来改变气隙大小，不同气隙下仿真得到的输出电压幅值与轴向位移关系如图9 所示。图中曲线的斜率绝对值表示传感器的灵敏度，根据实际使用所需的量程，选择曲线最陡的0.8 mm 范围作为线性区计算其灵敏度。

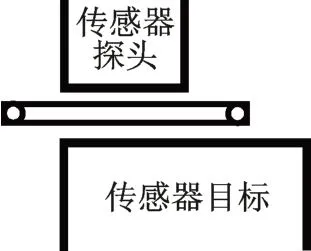
图8 仿真传感器目标初始位置Fig.8 The initial position of sensor target in simulation

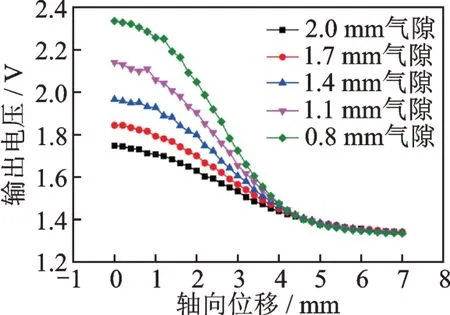
图9 不同气隙下仿真得到的输出电压幅值与轴向位移关系Fig.9 The relationship between the amplitude of the induced electromotive force and the axial displacement of the rotor under different air gaps in simulation

由图9 可以看出，气隙越大，线性区斜率绝对值越小，灵敏度越低。

通过仿真得到灵敏度与气隙的关系曲线如图10 所示。由于仿真精度和收敛性等原因，仿真结果有小幅抖动。

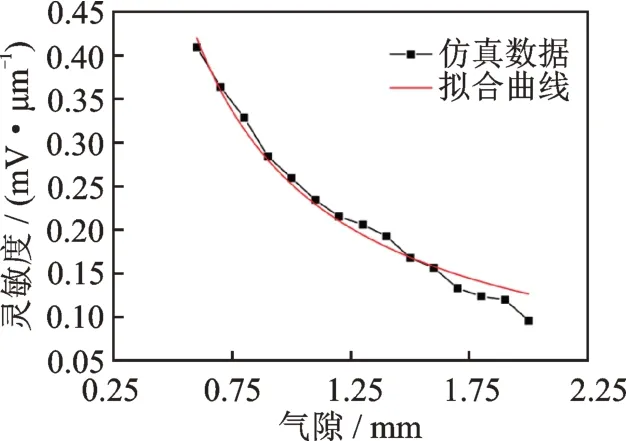
图10 灵敏度与气隙的关系曲线Fig.10 The relation curve between sensitivity and air gap

使用式（6）对仿真得到的数据进行拟合，有

δ的变化范围在0.6~2.0 mm 之间，可以看出分母中的常数项很小，可以忽略。

使用式（7）对仿真得到的数据进行拟合，有

结果与理论分析吻合较好，在0.6~2.0 mm 范围内，灵敏度与气隙大小近似成反比关系。

由图10 可以看出，气隙越小，传感器灵敏度越高。

2.3 实验结果

为验证理论与实际是否相符，构建了静态测试实验台如图11 所示，其中右下为集成式定子盘，每个激励线圈有58 匝。集成式定子盘与仿真模型相同，参数见表1。为去除径向位移导致的结果偏移，实验时使用位置相对的2 个轴向传感器同向串联，测量总感生电动势。

图11 静态测试实验台Fig.11 Static test bench

由于气隙为圆弧形，为更好地贴合传感器探头，传感器线圈使用柔性印刷电路板（flexible printed circuit，简称FPC）制作而成，其大小为28.5 mm×28 mm×0.3 mm，含有4 个线圈。传感器线圈实物如图12 所示，上方2 个线圈在FPC 内部反向相连，下方2 个线圈在FPC 内部反向相连，上下2 组线圈用于后续组成差分电路以提高灵敏度。FPC 共有4层，每层每个线圈为25 匝，故每个传感器共含2×100 匝线圈。传感器线圈厚度很薄，几乎不会增加传感器的体积。

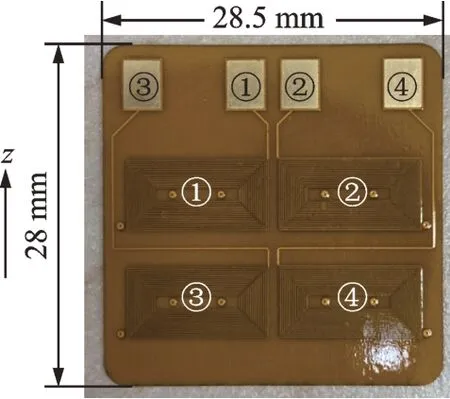
图12 传感器线圈实物Fig.12 The physical picture of sensor coils

对4 个激励线圈并联施加频率为40 kHz、峰峰值为40 V 的正弦激励电压，得到激励电压相同时不同气隙下感生电动势有效值与轴向位移间的关系以及传感器灵敏度，分别如图13 和表2 所示。由于实验条件的限制，仅进行2 组实验对理论和仿真结果进行验证。图中曲线的斜率表示传感器的灵敏度，根据实际使用所需的量程，选择曲线最陡的0.8 mm作为线性区，计算其灵敏度。

表2 激励电压相同时不同气隙下传感器灵敏度Tab.2 Sensor sensitivities under different air gaps when the excitation voltage amplitude is the same

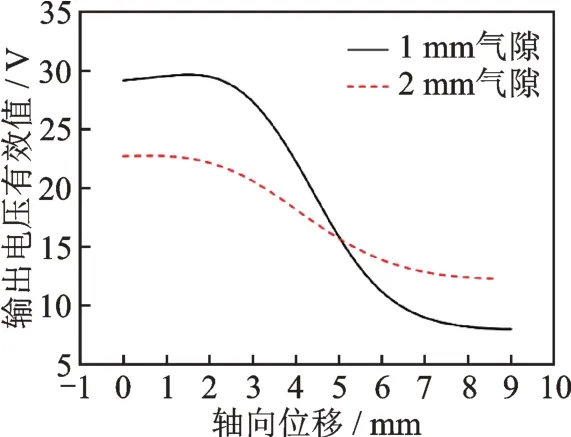
图13 激励电压相同时不同气隙下感生电动势有效值与轴向位移间的关系Fig.13 Relationship between the effective value of induced electromotive force and axial displacement under different air gaps when the excitation voltage amplitude is the same

实验结果表明，减小平衡气隙距离可有效提升传感器灵敏度，与理论分析和仿真结果一致。

由于气隙大小影响传感器的电感，不同平衡气隙的传感器激励电压相同时消耗的功率不同。最大输出功率是功率放大器的主要限制参数，因此有必要比较消耗功率相同时气隙对传感器灵敏度的影响。

对4 个激励线圈并联施加频率为40 kHz 的正弦激励电压，保持传感器消耗功率恒为30 W，得到消耗功率相同时不同气隙下感生电动势有效值与轴向位移间的关系以及传感器的灵敏度，分别如图14 和表3 所示。

表3 消耗功率相同时不同气隙下传感器灵敏度Tab.3 Sensor sensitivities under different air gaps when the consumed power is the same

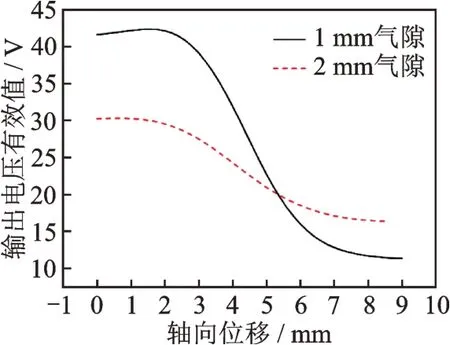
图14 消耗功率相同时不同气隙下感生电动势有效值与轴向位移间的关系Fig.14 Relationship between effective value of induced electromotive force and axial displacement under different air gaps when the consumed power is the same

实验结果表明，消耗功率不变的情况下，减小平衡气隙距离仍可有效提升传感器灵敏度。

综合仿真和实验结果可以得到：气隙越小，传感器灵敏度越高。但由于在传感器目标和传感器探头间加入了传感器线圈，气隙的大小应根据所需传感器灵敏度、传感器线圈厚度、工程安装精度及转子径向控制精度等因素综合设计。

3 电气参数对传感器灵敏度的影响

3.1 理论推导

在传感器机械尺寸固定的情况下，为在功率放大器驱动能力内充分发挥传感器的最佳性能，笔者研究了该传感器的电气参数对灵敏度的影响，首先分析感生电动势与电气参数间的关系。

为便于集成和安装，实际工程中一般使用集成式定子盘。将图2 中的激励线圈改为2 个缠绕在磁极上的匝数相同、绕线方向相反的激励线圈，使其产生的磁通相互增强。实际传感器结构如图15 所示，其中虚线为两磁极间的漏磁通。根据第1 节所述原理，为保证两磁极激励线圈产生的激励磁通量幅值恒定且相同，两激励线圈并联施加频率为f的正弦激励电压u0(t)。每个激励线圈的匝数均为N1，电流均为i(t)，两线圈产生的总激励磁通为Φ(t)。该传感器的等效磁路如图16 所示。

图15 实际传感器结构Fig.15 Actual sensor structure

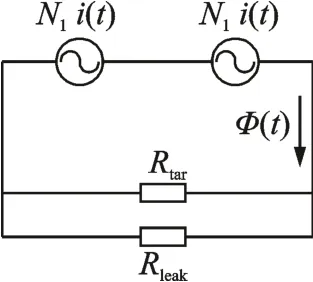
图16 图15 的等效磁路Fig.16 Equivalent magnetic circuit of figure 15

Rtar为经过气隙和传感器目标磁路的磁阻，Rleak为漏磁场磁路的磁阻。设Rtotal为磁路总磁阻，有

根据磁路定理，有

传感器的等效电路如图17 所示，设每个磁极的激励线圈的等效电感为L。

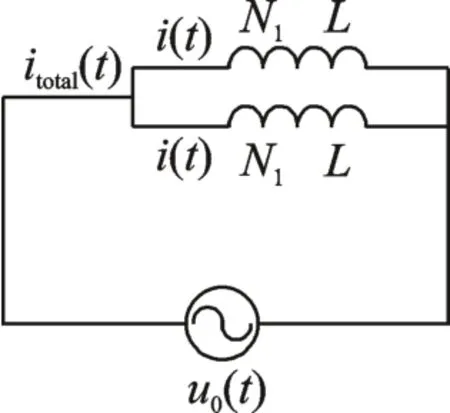
图17 等效电路Fig.17 Equivalent circuit

设激励电压为

根据电感两端电流与电压关系可得

代入式（13），得

设传感器线圈中通过的磁通量为Φ′(t)，当转子位置不变时，通过传感器线圈的磁通量与激励线圈产生的磁通量间存在固定的比例关系。设比例系数α<1，有

设串联后的传感器线圈的总匝数为N2，根据法拉第电磁感应定律可得感生电动势uind(t)为

电感传感器中电感的表达式为

其中：N为激励线圈匝数；A为传感器探头和传感器目标的重叠面积；l为传感器材料中的磁路长度；μr为传感器材料的相对磁导率；δ为转子和传感器探头间的气隙距离。

根据式（19），当转子和定子位置不变且无外磁场时，电感只与激励线圈匝数有关。设

代入式（18），得

感生电动势的幅值为

最大输出功率是驱动激励线圈的功率放大器的重要限制参数，功放在驱动线圈时的最大输出功率对应线圈的最大视在功率。由于激励频率升高会导致涡流效应显著，降低传感器灵敏度［16］，因此激励频率是传感器的另一限制参数。感生电动势与视在功率和激励频率的关系推导如下，由式（15）得单个激励线圈上的电流幅值为

传感器探头的视在功率S为

解得

将式（25）代入式（22），得

当传感器尺寸固定且定子和转子位置不变时，前面的系数均为定值，由此得到

传感器灵敏度Ssen为转子移动单位距离感生电动势幅值或有效值的变化量，因此有

在设计电路参数时，应以激励线圈的视在功率为传感器灵敏度的制约条件。为达到更高的灵敏度，在功放的最大输出功率范围内选取尽量高的输出功率，根据涡流效应的限制选取尽量高的激励频率。功放的最大输出电压作为次要限制参数，可在功率和激励频率确定后，通过调整绕线匝数使所需激励电压幅值在功放输出能力之内。根据式（25）等比例调整激励电压和绕线匝数将不会改变传感器的灵敏度。

3.2 实验验证

3.2.1 功率对感生电动势和灵敏度的影响

传感器气隙为2 mm，2 个传感器探头径向相对安装，得到的输出电压同向叠加，可消除由于径向位移导致的输出偏移。对4 个激励线圈并联施加频率为40 kHz 的正弦激励电压，通过改变峰峰值来改变线圈消耗的总功率，得到感生电动势有效值与总视在功率间的关系，如图18 所示。

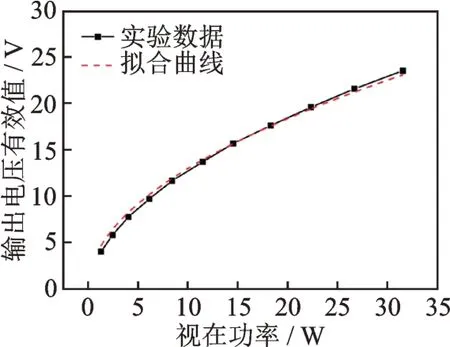
图18 感生电动势有效值与总视在功率间的关系Fig.18 Relationship between effective value of induced electromotive force and total apparent power

从曲线和拟合结果可以看出，实际与理论吻合得很好，感生电动势与视在功率符合下述关系

测量40 kHz 正弦激励下不同功率时感生电动势有效值与轴向位移的关系，如图19 所示。选取曲线最陡的0.8 mm 作为线性区，计算得出灵敏度与功率如表4 所示。

表4 灵敏度与功率Tab.4 Sensitivity and power

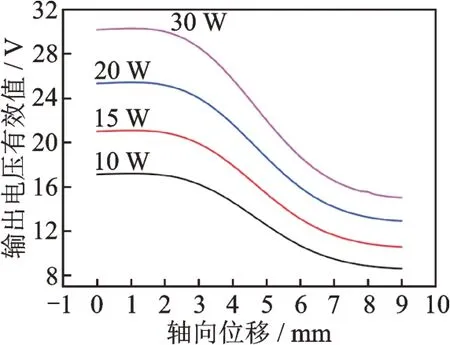
图19 不同功率下感生电动势有效值与轴向位移的关系Fig.19 Relationship between effective value of induced electromotive force and axial displacement under different power

根据式（28）对功率和灵敏度进行拟合，有

可以看出，实际与理论吻合得很好，灵敏度与视在功率符合下述关系

3.2.2 频率对感生电动势和灵敏度的影响

传感器气隙为2 mm，对4 个激励线圈并联施加正弦激励电压，改变激励频率并通过改变峰峰值使不同频率下线圈消耗的总功率相同，得到感生电动势有效值与激励频率间的关系，如图20 所示。

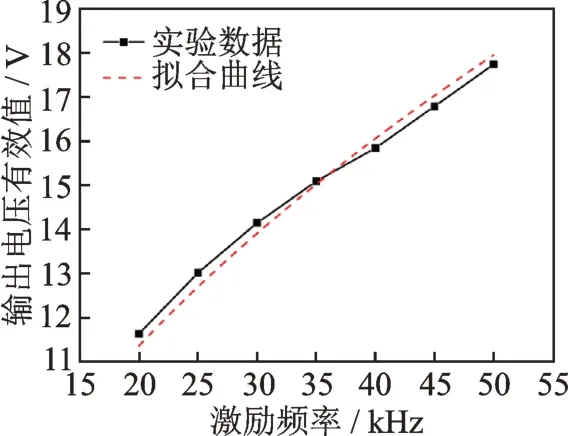
图20 感生电动势有效值与激励频率间的关系Fig.20 Relationship between effective value of induced electromotive force and excitation frequency

由于保证功率相同需要测量电流并手动调节激励电压，因此误差较大，所以R2相对较低，但仍在可接受范围内。

从曲线和拟合结果可以看出，实际与理论吻合得很好，感生电动势与激励频率符合下述关系

测量相同功率下不同激励频率时感生电动势有效值与轴向位移的关系，如图21 所示。选取曲线最陡的0.8 mm 作为线性区，计算得出灵敏度与频率如表5 所示。

表5 灵敏度与频率Tab.5 Sensitivity and frequency

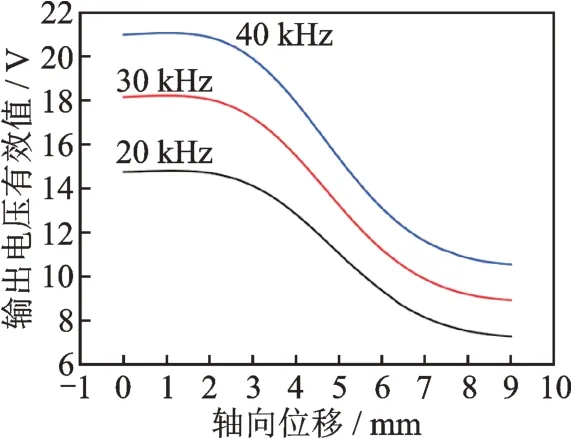
图21 不同频率下感生电动势有效值与轴向位移的关系Fig.21 Relationship between effective value of induced electromotive force and axial displacement under different excitation frequency

根据式（28）对频率和灵敏度进行拟合，有

可以看出，实际与理论吻合得很好，灵敏度与激励频率符合下述关系

通过综合使用本研究给出的提升传感器灵敏度的方法设计传感器参数，将传感器灵敏度从最初的2.5 mV/μm 提升至14.4 mV/μm，获得了良好的提升效果。

4 结束语

恒磁通电感位移传感器是一种新型的可有效抵抗外磁场干扰的电感传感器，传感器参数将影响其灵敏度。针对该传感器新式的结构和测量方法，研究了该传感器参数与灵敏度间的关系。理论和实验表明：平衡气隙越小，传感器灵敏度越高，且灵敏度与气隙大小近似成反比；激励频率和激励线圈消耗的视在功率越高，传感器灵敏度越高，且灵敏度与两者的算术平方根均成正比。基于功率放大器输出能力的限制，本研究给出的最大化传感器灵敏度的参数设计方法为：选用合适的气隙大小，适当提高激励频率并以激励线圈的视在功率为传感器灵敏度的制约条件，条件允许情况下尽量增大激励线圈消耗的视在功率，然后同比例调整激励电压和激励线圈匝数，使激励电压满足功放输出限制。