某超大跨度屋盖风压分布的风洞试验∗

林韬略， 谢壮宁， 冯 帅，2， 张乐乐， 汤 亮

（1.华南理工大学亚热带建筑与城市科学全国重点实验室 广州，510640）

（2.中建四局华南建设有限公司 广州，510700）

（3.中国建筑第二工程局有限公司华南分公司 深圳，518048）

（4.广东工业大学经济学院 广州，510006）

引 言

大跨屋盖结构一般处于大气边界层中湍流强度较高的近地面区域，属于风敏感性和风易损性结构，其在强（台）风作用下主体结构的破坏并不常见，但屋面围护系统受损情况却常有发生［1］。在此类结构的抗风设计中，首要关注的就是屋面的风压分布特征。程志军等［2］分析了平屋面等几种规则屋面的分布特征，并论述了屋面结构的风致破坏机理。关于低矮房屋屋面抗风设计的风压取值，主要依照《建筑结构荷载规范》［3］和《屋盖结构风荷载标准》［4］中的建议和模型风洞试验，但相关研究工作基本上都是以普通的小尺度低矮房屋建筑为对象进行的，考虑到外形的复杂性，已有规范的建议不一定适用于新建的大跨度屋盖结构的抗风设计。大跨结构屋面的风压分布主要是通过风洞试验获取，如对于大跨度体育场看台悬挑雨棚的研究。张建等［5］发现波纹状屋面的极值负压绝对值要比光滑表面屋盖增加13%。刘慕广等［6］发现屋面局部不到5°的倾角变化会使得最不利极值负压绝对值增加15%。郑怡彤等［7］研究了周边建筑对大跨度煤棚风荷载的影响，发现周边建筑的干扰对于煤棚的风荷载体型系数不容忽略。

当屋盖结构跨度相对较小时，采用整体模型进行风洞试验能够满足试验精度要求。对于超大跨度屋盖结构若采用整体模型进行风洞试验，将导致模型的几何缩尺比较小，使得模型局部形状、细节以及相应风场指标难以得到较好的模拟，从而很难保证试验结果的可靠性。风工程实践中一般不建议采用太小的模型进行风洞试验。

大跨度屋面的风损部分原因是屋面极值风压可能没有得到可靠的估计［8］，近些年风压的非高斯分布特性在风压极值统计中得到了广泛的关注［9-13］。观测极值法［14］是估计极值风压常用的一种统计方法，其原理简单，物理意义明确，但是只有在处理长时程数据时才能获得较为准确的结果。通常风洞试验一般只进行较短时程的风压测量，直接按照10 min 时距进行分段得到的子样本数较少，统计结果随机性较高，结果稳定性差。Feng 等基于互信息理论［15］提出了针对样本独立性的判定方法和相应的极值统计方法，并已验证使用基于互信息的观测极值法进行大跨度屋盖结构极值风压的估计，比其他常用的短时程极值估计方法具有更好的稳定性与精度［16］，但不足之处是该方法在分析样本独立性确定最佳的样本分段长度时需要花费大量的计算时间。

针对以上问题，根据已有不同类型模型风洞试验的统计分析结果，确定出适用于风压时程独立性分段的最小分段时距，形成简化的基于互信息的观测极值法。笔者以跨度达1.7 km 的深圳国际会展中心为研究对象，采用节段模型方法对该超大跨度屋面系统进行了风洞试验，分析了屋面风压分布特征并对其节段模型方法进行验证。通过分析会展中心不同展馆之间的相互干扰影响，给出会展中心屋面系统的取值建议。

1 试验概况

1.1 工程背景

深圳国际会展中心建筑效果如图1 所示，主要是由10 个展厅、2 个登陆大厅和1 条中央廊道组成的超大跨屋盖结构。屋盖东西两侧边沿为波浪形悬挑结构，在同侧相邻的2 片屋盖之间存在内部中间街道。

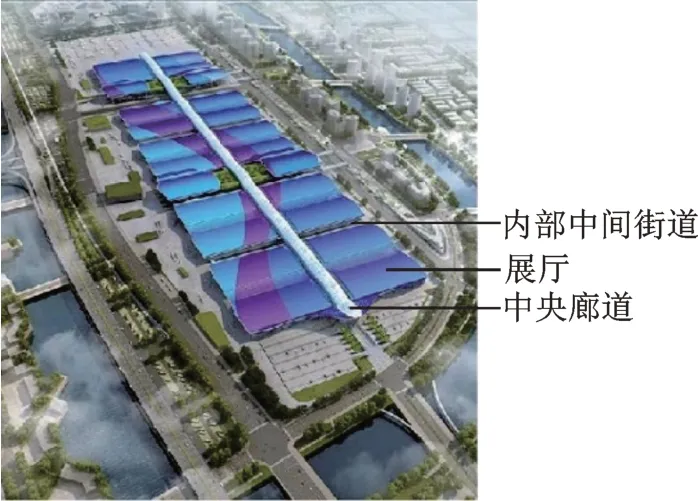
图1 深圳国际会展中心建筑效果图Fig.1 Architectural renderings of Shenzhen International Convention and Exhibition Center

1.2 风洞试验概况

由于该会展中心跨度较长，无法实现整个建筑群的风洞同步测压试验，因此根据该建筑结构的对称性特征，综合考虑其大小和风洞试验段尺寸，模型的缩尺比取为1∶250。采用节段模型方法分别进行了5 次不同的风洞试验，分批试验及风向角示意如图2 所示，节段模型试验时将适度考虑其相邻展厅的影响。由于屋盖四周场地较空旷，周边建筑的干扰作用影响较小，故只在被测模型四周放置一定范围的屋盖补偿模型。图3 为试验模型照片，为评估不同展厅之间的相互干扰影响，对展厅A 的单体进行了试验。依靠少量局部节段模型及模型上的测压点，最终完成上下屋盖表面共5 060 个测点的所有展厅风荷载全测量。

图2 分批试验及风向角示意图Fig.2 Schematic diagram of batch experiment and wind direction angle

图3 试验模型照片Fig.3 Photos of experiment model

该建筑为超大跨屋盖结构，笔者已完成该超大跨建筑结构的标准展厅单体结构的风振响应分析［17］。围护结构尺寸一般较小且自振频率相对较高，通常不考虑围护结构的风致振动［18］，而应重点关注围护结构的全风向风荷载极值分布，故进行准确的极值风压估计尤为重要。

刚性模型测压试验开展于华南理工大学风洞实验室。试验流场地貌按照《建筑结构荷载规范》［3］中规定的A 类地貌模拟，平均风速剖面和湍流度剖面如图4 所示。为便于分析，试验中统一以0.8 m（原型200 m）处作为参考高度，参考风速Ur达12.1 m/s，并对水平风速剖面做无因次化处理。图5给出了屋面所在高度水平脉动风速功率谱，其中：Su(f)为水平脉动风速功率谱；f为频率；Lu为湍流积分尺度；U为参考高度水平平均风速；σ2u为水平脉动风速均方根值。风场模拟情况良好，试验结果与理论Karman谱吻合度较高。

图4 平均风速剖面和湍流度剖面Fig.4 Mean wind speed profile and turbulence intensity profile

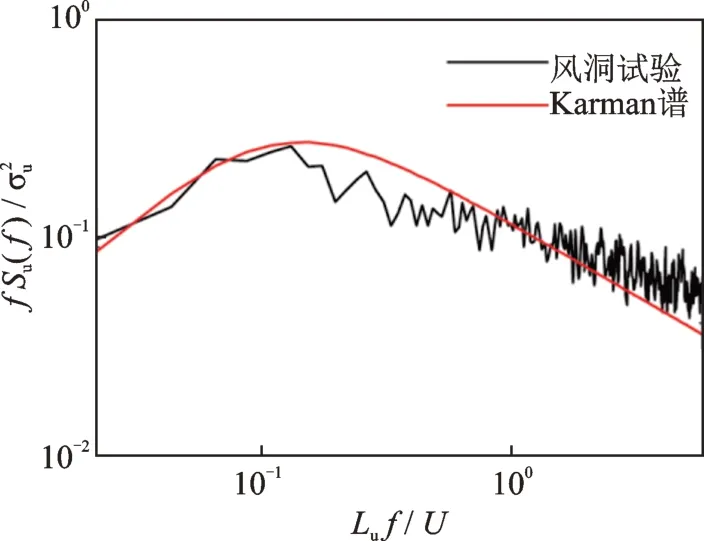
图5 屋面所在高度水平脉动风速功率谱(Z = 25 m)Fig.5 Fluctuating wind velocity power spectrum at the height of roof (Z = 25 m)

风压系数时程单次采样时长约为62 s，折算为原型采样时长约为63 min，采样频率为330 Hz，样本长度为20 480。取10°为风向角间隔，共测量36 个风向角。为保证客观性，试验中统一以0.6 m（原型150 m）作为无因次化的风压参考高度。风压系数的表达式为

其中：Cpi(t)为i处测点的风压系数；Pi(t)为i处测点的风压；Ur为风压参考高度处的风速；P0为风压参考高度处的静压。

2 极值风压估计方法

2.1 基于互信息的观测极值法简介

《屋盖结构风荷载标准》中规定，当风压系数时程不小于250 min 时，可将风压系数时程Cp(t)按10 min 时距等分为N个子样本，然后挑选出每个子样 本 中 最 大 值Cpi，max与 最 小 值Cpi，min，分 别 组 成 极 值样本，并计算其算术平均值作为整个风压系数极大值Cp，max与极小值Cp，min，即

上述过程即为峰值分段平均方法，属于观测极值法，其隐含了所划分的10 min 样本之间是相互独立的基本假定（通常都能满足这个假定）。但该方法要求分段数至少达到25，出于经济性和效率的考虑，常规风洞试验采集的样本数很难满足此要求。

文献［13］提出的基于互信息观测极值法，较好地解决了风压数据子样本之间的样本独立性判定的难点，并依此确定最佳的独立样本分段观测短时距t1，采用峰值分段平均方法初步估算出极值风压系数，再通过不同分段时距间的极值转换关系进行补偿，最终获得短时程风压样本基于目标观测长时距t2（如10 min）下的极值估算为

其中：Cpi，max，t1，Cpi，min，t1分别为观测短时距t1时每个子样本的最大与最 小值；σmax，t1，σmin，t1分别为 观测短时距t1时极大与极小值样本的标准差；等号右端的第1部分为观测时距t1下的极值；第2 部分为时距t1转换到t2的补偿值（补偿值在极值风压转换中起重要作用，没有补偿会导致极值估计不准确）；B1，B2为和样本数N有关的常数。

2.2 简化方法及其有效性验证

基于互信息的观测极值法的不足之处是在确定独立观测短时距t1时耗时较长，计算效率差。因此，为方便实际工程项目应用，基于该方法对多个风洞试验模型风压时程进行独立性分析，取最小独立观测时距的包络值，其结果均没有超过600，故在实际计算中直接取600 点对应的时间t1进行极值统计，则式（3）中B1，t1和B2，t1分别确定为1.125 7 和0.539 4，则式（3）简化为

式（5）中B2，t2的值与选择的观测长时距t2有关，按照我国规范标准，长时距一般取为10 min，即t2=600 s。本研究将以上方法称为简化的互信息观测极值法（简称为简化方法）。笔者针对6 个不同缩尺比（1∶45~1∶500）风洞模型的统计分析结果，进一步验证了这种方法的可靠性［19］。

选取深圳国际会展中心标准展厅单体A 屋盖全部墙面与屋面的上表面测点计算极值风压系数，选择180°正风向角和140°斜风向角（风向角示意图如图2 所示），Cp，min，j和Cp，min分别为采用简化方法和严格基于互信息的观测极值法估算的极小值结果，如图6 所示。简化前后的2 种极值统计方法所估算的极值风压系数线性回归效果理想，数据整体关联性强，决定系数R2非常接近1。此结果优于文献［19］针对其他不同模型的统计分析结果，其部分原因和600 点是取值包络结果有关，这进一步验证了采用简化方法的有效性。

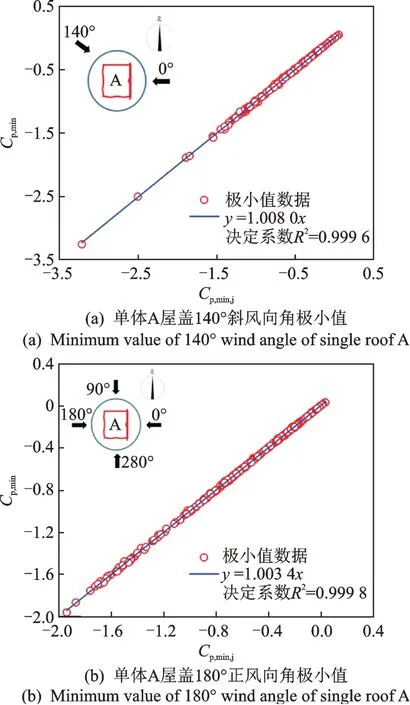
图6 简化方法与基于互信息的观测极值法极值结果对比Fig.6 Comparison of extreme value results between simplified method and observation extreme value method based on mutual information

简化方法与基于互信息的观测极值法具有一致的数值稳定性和计算精度，且简化方法省去了确定独立观测短时距t1的时间，具有更高的工程计算效率。

本研究以600 个采样点作为独立分段依据，是根据华南理工大学风洞试验的特定不同缩尺比模型的试验结果统计得到，并且是在330 Hz的采样频率下获取的，对于其他采样频率的电子扫描测压系统，应根据实际设备的采样频率做相应的调整。不同实验室或其他模型试验结果可能有所不同，流场湍流特性、模型的复杂程度会影响满足样本独立性的样本长度，建议具体环境具体分析，或进一步调大采样点数。

3 风压分布的试验结果

3.1 节段模型试验的可行性验证

为验证节段模型方法的可行性，分别选取两个批次节段试验的180°风向角下A 屋盖西北角和相邻的N 屋盖西南角，其风压系数连续性如图7 所示。尽管有内部中间街道间隔，由两批次试验得到的A和N 屋盖相邻区域的极值风压系数与平均风压系数分布仍呈现非常好的连续性。

图7 180°风向角相邻屋盖A 和N 风压系数连续性Fig.7 Continuity of wind pressure coefficients of adjacent roofs A and N at 180° wind direction angle

3.2 标准单体屋盖与屋盖建筑群风压分布对比

选取标准展厅单体A 屋盖与考虑了相邻展厅影响的屋盖建筑群进行2 次试验，将4 个不同风向角下屋面的极小风压系数分布进行比较，A 屋盖单体工况与建筑群工况极小风压系数如图8 所示。

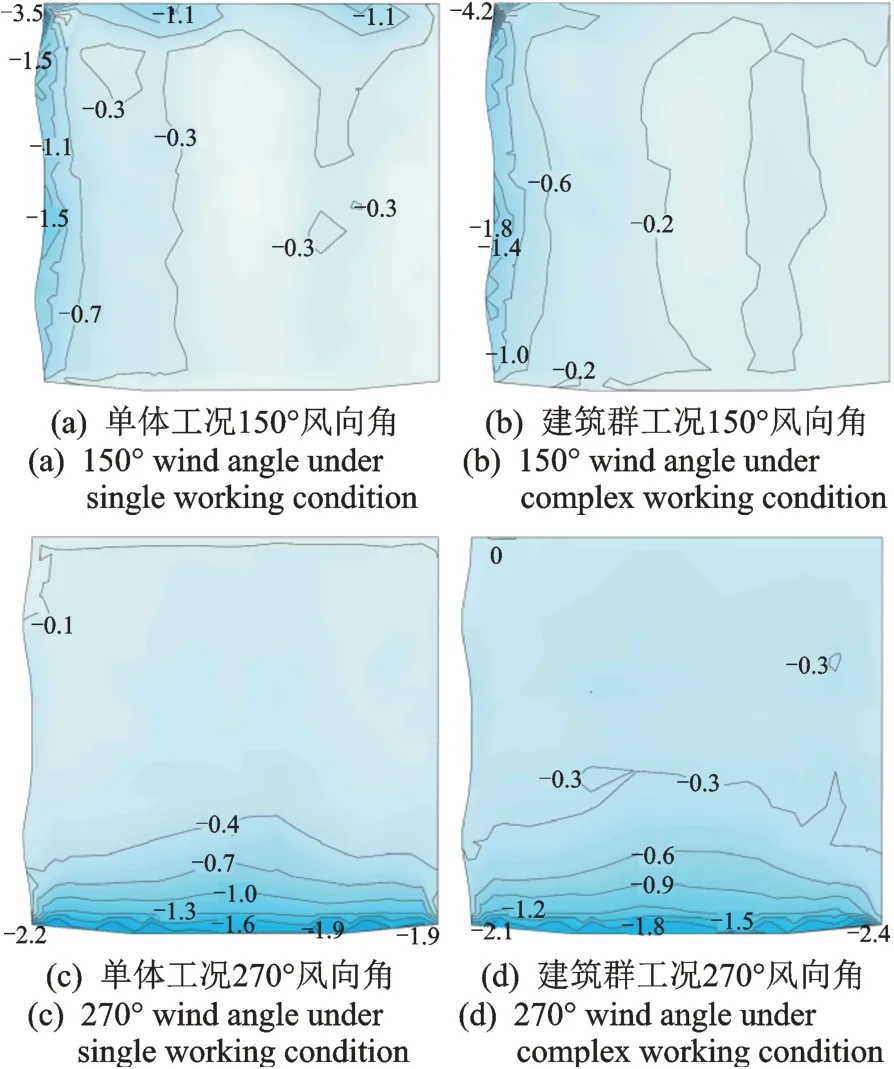
图8 A 屋盖单体工况与建筑群工况极小风压系数Fig.8 Minimum wind pressure coefficient of roof A between single building condition and building group condition

在150°风向角下，屋盖会产生锥状涡，涡区的风吸力较大且变化梯度剧烈。由于屋盖A 与屋盖N间内部街道的干扰作用，使得局部流场的加速效应进一步加大了屋盖A 西北角区的风吸力，极小风压系数从-3.5 降至-4.2，吸力值升高了20%，干扰系数达1.2。270°风向角时，由于建筑群工况下两相邻展厅间中央廊道的局部流场具有加速效应，使得屋盖A 东南角区的极小风压系数较单体工况的小，极小风压系数从-1.9 降低至-2.4，吸力值升高了26.3%，干扰系数达到1.26。

3.3 屋盖的整体风压分布特征

根据全风向角综合拼接处理的整体屋盖的风压系数包络值，结合深圳市50 年重现期的基本风压0.75 kN/m2及风气候特征，最终以分块方式给出可用于屋面抗风设计的风压标准值。限于篇幅，这里仅给出南面A，M，N 和P 展厅屋盖的风压分布（其特征规律同样体现在Q，R，S 和T 这4 个相邻屋盖），全风向角最小负压分块分布如图9 所示。

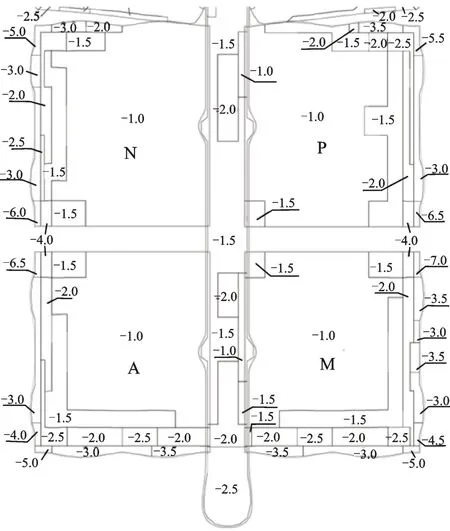
图9 全风向角最小负压分块分布（单位：kPa）Fig.9 Block distribution of minimum negative pressure at all wind angles (unit:kPa)

该超大跨度屋盖结构整体风压分布沿中央走廊呈现出较为明显的轴对称特征，每个屋盖中部大面积区域负压相对较小，为-1.0 kPa；边角区域的负压相对较大，最高的负压值为-7.0 kPa，出现在位于靠近内部中间街道的展厅屋盖角区；其他部位的负压分布在-3.0 kPa~-5.0 kPa 之间。因此，屋面抗风设计对于这些部位应给予足够的关注。

4 结 论

1） 对于超大跨度屋盖结构风洞试验，采用局部节段模型进行多批次试验是有效和可靠的。

2） 采用经验分段点数对已有基于互信息的观测极值方法进行简化，可以在提高计算效率的情况下获得和基于互信息的观测极值方法相当的统计精度。

3） 周围屋盖的干扰会造成风压绝对值的放大效应，使相邻屋盖角区的负压增大，干扰系数最大可达1.26。

4） 超大跨屋盖整体结构的高负压主要分布于角区，最高负压出现在靠近内部中间街道的屋角，达到-6.0 kPa~-7.0 kPa，明显高于远离内部中间街道的屋角。