通过整体叶盘切缝的振动抑制方法初探∗

赵 睿， 罗华耿

（厦门大学航空航天学院 厦门，361000）

引 言

随着材料科学的发展以及相关加工工艺的进步，航空发动机整体叶盘逐渐取代榫接叶盘。与榫接叶盘相比，整体叶盘具有轮盘薄、质量轻等优点，且没有榫头与榫槽的摩擦与碰撞，因此降低了材料的磨损。但是，整体叶盘的轮盘及叶片质量与刚度相差较小，容易发生耦合振动［1］；整体叶盘阻尼较小，容易产生高周疲劳破坏；此外在制造及运行过程中难以避免叶盘失谐现象的发生，其产生的振动局部化问题也易导致振动破坏［1］。因此，研究涡轮叶盘系统的振动抑制机理、探索有效的振动抑制方法具有重要的现实意义，是发动机振动抑制领域的热点之一。

针对整体叶盘振动抑制，最常用的减振方法是从增加摩擦阻尼或碰撞增加额外阻尼入手［2］。基于增加摩擦阻尼进行振动抑制的方法［3-4］已有初步探索。文献［5-6］通过在涡轮叶盘的轮缘内侧靠近根部位置安装阻尼环，提出了带摩擦阻尼环整体叶盘的非线性动力学分析方法，取得了较好的振动抑制效果。Green 等［7］依据硬涂层中涂层颗粒之间的内部摩擦能够达到振动抑制效果的理论，利用实验验证了此减振机理的正确性。Allara［8］基于涡轮叶片的接触摩擦模型，提出了一种利用接触刚度和摩擦因数来模拟表征摩擦接触面刚度和阻尼的方法。Wei 等［9］研究了干摩擦阻尼和黏性阻尼对循环对称结构局部振动的影响，得出两类阻尼均可降低结构局部振动的结论，且干摩擦阻尼比黏性阻尼更易影响振动局部化。陈香等［10］设计了涡轮整体叶盘带冠叶片的干摩擦阻尼振动抑制实验方案，分析了不同阻尼参数阻尼块的减振抑制效果，实验结果为干摩擦阻尼器设计参数的选取提供了数据支持。陈璐璐等［11］通过数值方法优化叶盘叶片的凸肩位置，从而实现抑制叶片的振动响应。

许多学者对基于碰撞增加额外阻尼振动抑制的方法也进行了研究。Kaneko 等［12］研究了在旋转状态下的自带冠叶片，结果表明，由于离心力的存在使叶冠在冠间发生碰撞，消耗了叶片的振动能量并最终实现振动抑制。Lu 等［13-14］研究了含有碰撞阻尼器系统的振动，包括单自由度系统结构参数的改变以及两自由度系统激励方式的改变对碰撞阻尼器振动结果的影响，研究表明，增加一定程度的阻尼质量比能够提高阻尼器的减振效果。卢绪祥等［15-16］研究了自带冠叶片碰撞减振机理，得知碰撞振动表现为非线性。赵亚英等［17］基于有限元分析软件对带冠叶片的碰撞过程进行了有限元仿真，得出叶冠间隙在一定范围内通过碰摩可以有效减少振动的结论。

笔者提出了一种新的整体叶盘阻尼减振方法，通过在整体叶盘的设计过程中进行切缝处理，并补以高阻尼材料，使得叶片受外激励下振动时，叶盘间隙发生碰撞和摩擦，从而引起振动能量的耗散，为整体叶盘提供了额外阻尼，实现整体叶盘振动抑制的目的。首先，根据分段非线性模型，建立了叶盘扇区的动力学模型，并进行数值仿真模拟分析；其次，开展扇区、整体叶盘模态测试实验，并基于希尔伯特变换法进行参数辨识；然后，分析了不同碰撞条件下的结构阻尼变化规律，并依据模态测试结果修正仿真模型参数；最后，总结了所提出的整体叶盘减振方法的可行性，为后续整体叶盘结构减振设计提供思路。

1 叶盘扇区动力学模型的建立及仿真分析

1.1 单自由度仿真模型的建立

叶盘切缝如图1 所示。选取循环对称叶盘结构的一个扇区，简化为一个单自由度双侧带间隙非线性振动模型，如图2 所示。

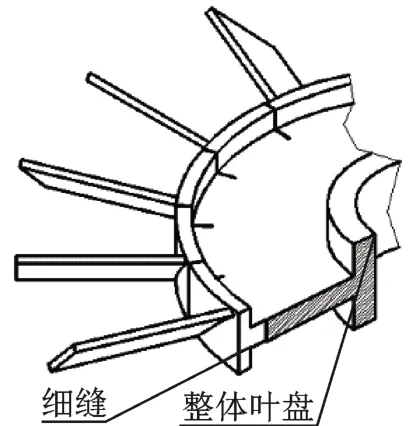
图1 叶盘切缝Fig.1 Model of a blisk with slitting

图2 带间隙非线性振动模型Fig.2 Dynamics model of a blisk with slitting

叶盘模型的运动微分方程如下

其中：m为质量；k1，k2为系统刚度；c1，c2为系统阻尼；k3，k4分别为系统左右两边的碰撞刚度；δ0为细缝间隙；F为作用于系统的外力；a0为外力的幅值；f00为外力的激励频率；k（x）为结构恢复力；x为沿轮盘切线方向位移，即叶盘周向位移。

通过调整参数大小，可以模拟分析叶片在不同参数下的振动响应规律。

对上述运动微分方程做如下归一化处理

其中：f0为固有频率；k0=2k1=2k2；c0=2c1=2c2；β，γ为无量纲参数。

将式（1）~（3）写成统一形式，可得

其中：ωi为分段线性每一段的固有圆频率；Fi为分段线性每一段的等效外激励N。

1.2 基于希尔伯特变换的结构瞬时特征参数估计

基于希尔伯特变换的非线性参数识别方法［18-22］是将非线性系统等效为一个线性时变系统，实现对时变参数的识别。式（10）~（12）是一个分段线性系统，很难直接将这样的系统参数描述为显式时变参数，但可以将其等价为一个时变参数的系统。

具有等价黏性阻尼的线性时变单自由度系统的自由振动微分方程为

若已知结构在自由振动条件下的位移响应、速度响应、加速度响应以及对应的希尔伯特变换，就能识别出结构的时变模态参数，其计算式为

其中：f0（t） 为无碰撞条件下的线性系统的固有频率；ς0（t）为阻尼比；m（t）为质量；ẍ(t)和ẍ̂(t)为加速度响应及其希尔伯特变换；ẋ(t)和ẋ̂(t)为速度响应及其希尔伯特变换；x（t）和x̂(t)为位移响应及其希尔伯特变换。

为简化表达，后文中速度响应表示为v（t），加速度响应表示为a（t）。

1.3 扇区模型数值算例分析

对上述单自由度系统，分别计算线性与非线性系统的自由衰减响应，为后续分析做参考。令外激励Fi=0 N，固 有 频 率f0=3.5 Hz，阻 尼 比ς0=1.55%，u0=0.021，γ=1。 设 系 统 的 初 始 位 移x（0）=5u0，初始速度v（0）=0。先取α=0，即碰撞刚度为0，此时系统为单自由度线性系统，即无碰撞引起的刚度非线性。线性与非线性状态下瞬时响应与参数识别结果对比如图3 所示。由四阶龙格-库塔法求解得到结构的位移、速度和加速度响应曲线如图3（a）所示。在其他参数不变的情况下，修改α=8，此时碰撞刚度为有限值，而且初始位移大于初始缝隙，所以系统为单自由度非线性系统，响应计算过程中会发生碰撞状态，计算所得结构的位移、速度和加速度响应曲线如图3（b）所示。

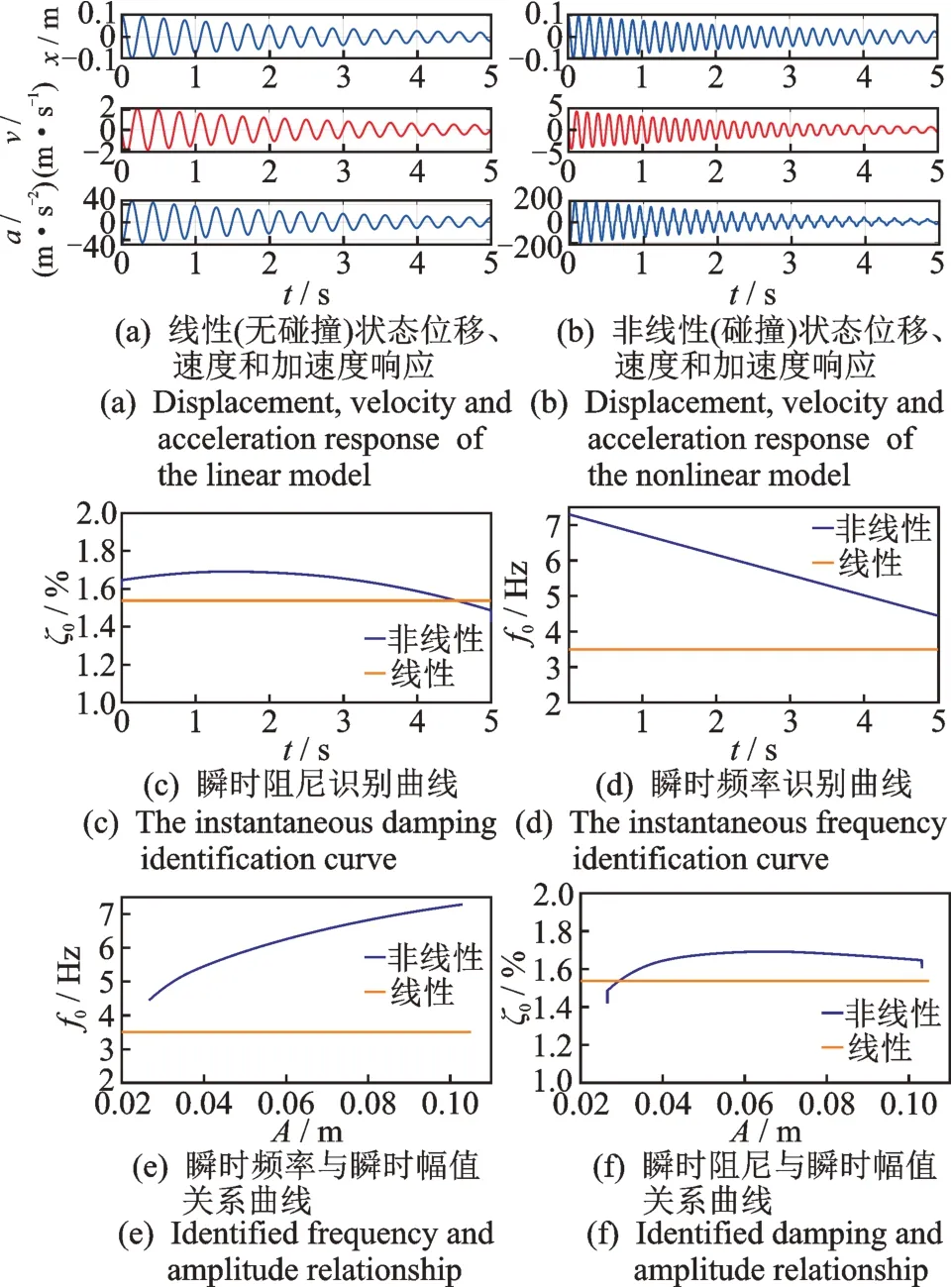
图3 线性与非线性状态下瞬时响应与参数识别结果对比Fig.3 Identified parameters from linear and nonlinear systems

根据式（14）和式（15）对响应信号进行相应的希尔伯特变换及数值微分计算，即可得到系统的瞬时模态参数，如图3（c，d）所示。其中，线性系统的识别结果与仿真中所设置的参数理论值一致，从而验证了识别单自由度结构的时变参数设置的正确性。同时可见，非线性状态时频率最大值略有上升，且阻尼大于线性状态。

由于参数识别假定了非时变参数的线性结构，所以图中所识别的系统参数（如瞬时频率以及瞬时阻尼）均为时变函数。另外，由于位移与时间的关系已知，所以所识别的时变参数也可以转化成位移的函数，如图3（e，f）所示。

2 实验验证

为了验证碰撞减振应用在整体叶盘振动抑制中的可行性，设计了模态测试实验来获取切缝叶盘的模态参数，通过不同结构、材料的叶盘模态参数比较，判断碰撞减振的实际效果。

2.1 实验总体设计

实验用力捶对切缝整体叶盘结构施加脉冲激振力，采用NI 数据采集仪对叶盘加速度数据进行采集，实验测试实况及部分仪器如图4 所示，本次实验的激励与加速度响应拾取均在垂直于叶盘面的方向上进行。

图4 实验测试实况及部分仪器Fig.4 Experimental setup and instrumentations

利用带通滤波以及希尔伯特变换，可以对分析频率范围内任意阶模态实施非线性参数识别。本研究仅对叶盘的第1 阶模态开展分析与讨论。

由于现有工艺的限制，叶盘加工缝隙能实现的最小尺寸为0.2 mm，所以仅依靠锤击激励产生的振动很难发生碰撞，因此在锤击实验时叶盘缝隙间填充了不同材料以增加叶盘的等效阻尼。

2.2 扇区结构瞬时特征参数识别实验

对铝合金填充的扇区叶盘进行实验，得到原始加速度响应信号及其傅里叶频谱如图5 所示。理论上，傅里叶变换是一个线性变换，为确定带通滤波的范围，对加速度信号a（t） 进行傅里叶频谱分析，用以判定加速度信号中第1 阶模态响应的频率范围，为滤波器设计提供参考。如扇区叶盘1 阶频率范围在820 Hz 左右，为此设计了截止频率为850 Hz 的低通滤波器，滤波后加速度、速度及位移响应信号如图6 所示。对加速度信号的一次和二次积分作适当的去趋势化，可分别得到速度与位移时间波形。

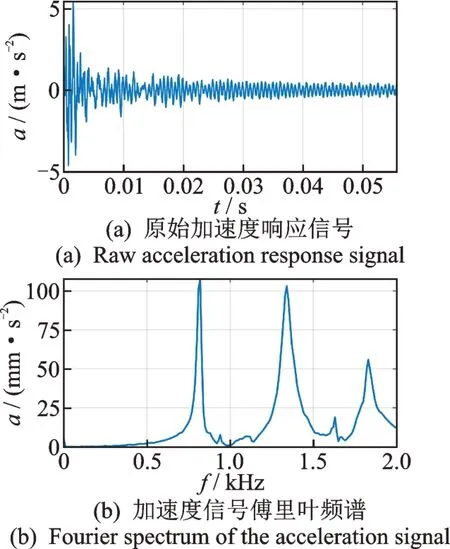
图5 原始加速度响应信号及其傅里叶频谱Fig.5 Raw acceleration response and its Fourier spec trum

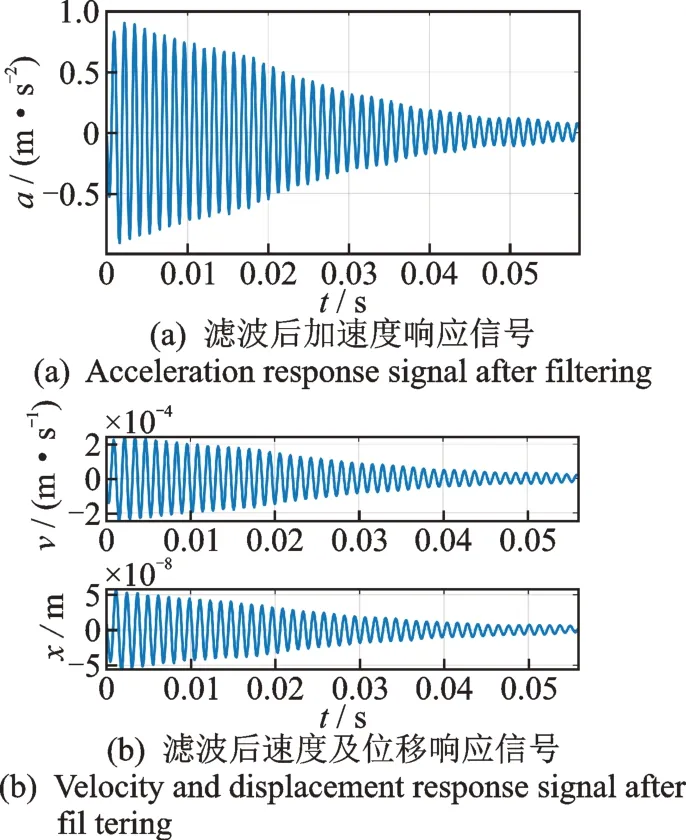
图6 滤波后加速度、速度及位移响应信号Fig.6 Acceleration, velocity and displacement response signal after filtering fil tering

扇区叶盘非线性参数识别结果如图7 所示，所识别的参数也可以表达成位移的函数，见图7（c，d）。

图7 扇区叶盘非线性参数识别结果Fig.7 Sector blisk nonlinear parameter identification results

2.3 单自由度仿真模型修正

因前述仿真模型并未考虑叶盘缝隙中填充材料的影响，为了尽可能使仿真模型更加贴近实验条件下的真实叶盘结构，本节基于模态实验结果对仿真模型进行修正。

缝隙填充后叶盘仍然可以看作是一个非线性系统，其非线性主要来自于以下方面：①填充材料本身的非线性；②填充材料与缝隙接触面在相对运动过程中的拉压非对称性。依据文献［18-22］，可将非线性系统等效为线性时变系统进行参数识别，因此在修改模型时等效成随位移变化的刚度和阻尼。由图7（c，d）扇区叶盘非线性参数识别结果，对原模型进行修正，修正后叶盘模型如图8 所示。其中：m（t）为质量；k1（x），k2（x）为系统的刚度；F为系统的外力且取0；c1（x），c2（x）为系统的阻尼；x为沿轮盘切线方向位移。

图8 修正后叶盘模型Fig.8 The revised blisk model

修正叶盘模型的运动微分方程如下

其中：c（x）为结构时变阻尼；k（x）为修正前结构恢复力；x为沿轮盘切线方向位移；ς0为阻尼比；kc（x）为修正后结构刚度。

将参数识别结果代入修正后的模型中并与实验结果进行对比，如图9 所示。结果显示，修正后的模型与实验结果吻合良好，表明模型修正方法的正确性，能够较好地反映真实叶盘结构的动力学特性。

2.4 整体叶盘结构特征参数识别实验

为验证不同的填充材料对等效阻尼的影响，本次实验采用了3 种不同的填充材料：铝膜、纸以及橡胶。时域响应如图10 所示，未切缝整体叶盘及切缝整体叶盘非线性参数识别结果如图11 所示，不同状态下参数识别结果对比如表1 所示。

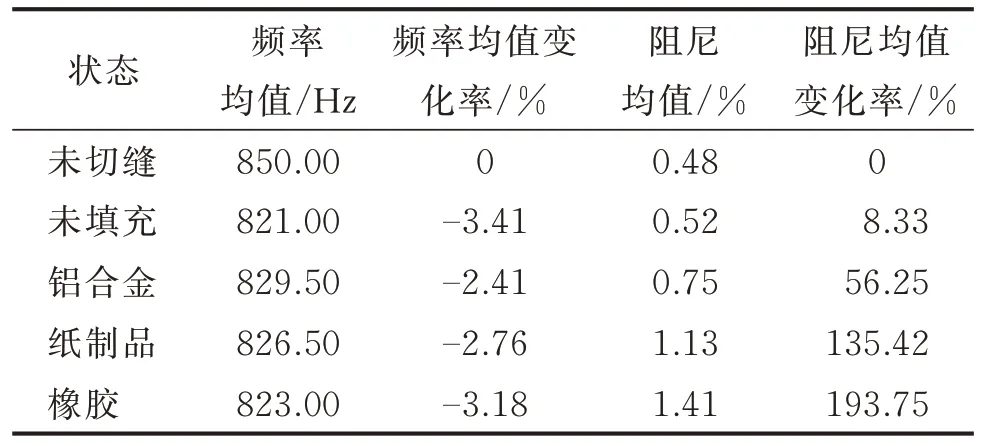
表1 不同状态下参数识别结果对比Tab.1 The parameter identification results under different condition

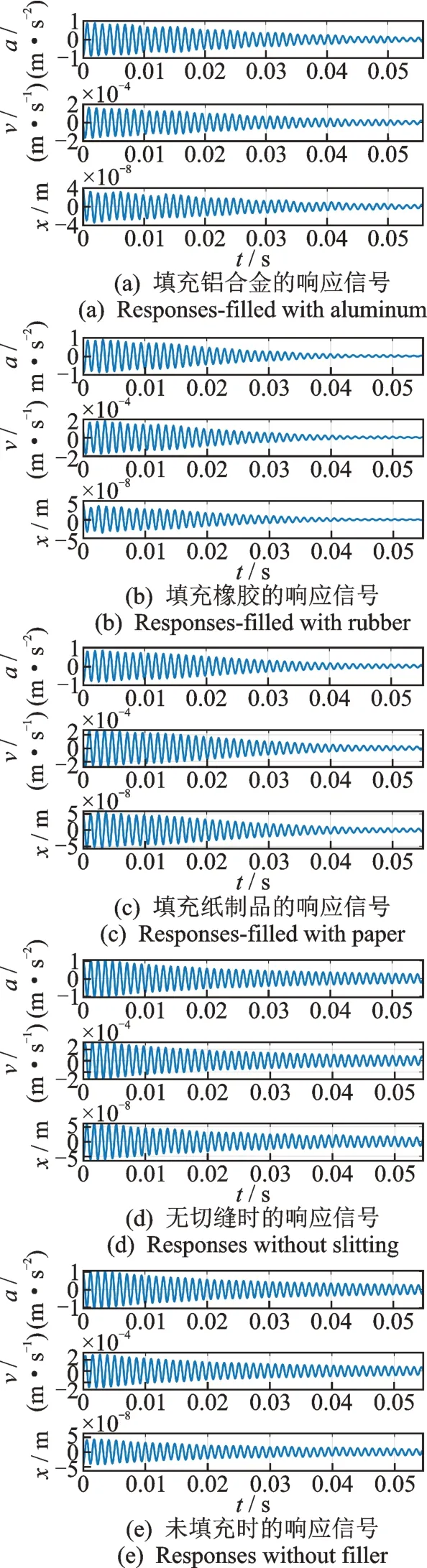
图10 时域响应Fig.10 Time domain response

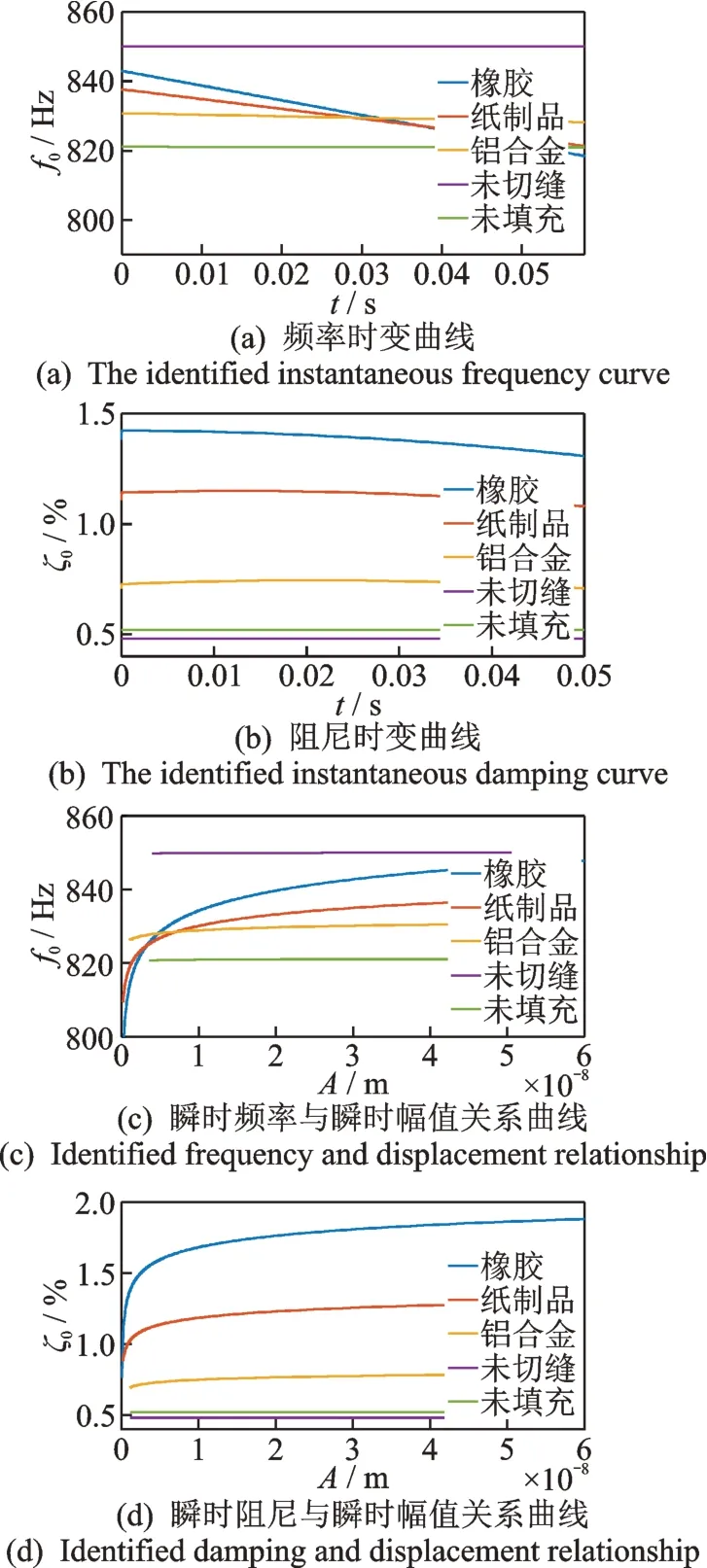
图11 叶盘非线性参数识别结果Fig.11 Nonlinear parameter identification results of blisk

对比图11 各状态下的振动时域响应可知：存在填充材料以及碰撞时的振动比无碰撞时的振动衰减速率更快；不同填充物对比结果显示，橡胶振动响应衰减速率最快；不同频率与阻尼的识别结果表明，未切缝整体叶盘和切缝未填充材料整体叶盘时的频率与阻尼数值基本恒定，验证了实验中的非线性现象是由填充材料以及碰撞因素所引起；存在不同填充物时，阻尼更大且阻尼及频率会随振动时间与幅值改变，与未填充状态相比频率均值有所增大；不同填充物的阻尼相比，橡胶＞纸制品＞铝合金，但均比未填充时阻尼大。因此，切缝填充物的阻尼有助于增加整体叶盘的阻尼。

3 结 论

1） 所设计的叶盘切缝对所分析的1 阶频率影响不大（小于4%）。

2） 可以通过切缝的碰撞增加振动的能量耗散，从而提高叶盘的阻尼比，但所增加的阻尼跟切缝的大小有关。

3） 切缝填充能进一步提高叶盘的阻尼，且阻尼大小与填充物的材料性质有关。本研究测试的切缝填充材料中，阻尼性能最好的橡胶将叶盘的等价阻尼提高到了未作处理时整体叶盘的约3 倍。

4） 由于目前实验室条件的限制，实验仅在叶盘静态时进行，未考虑旋转状态下离心力、转速等指标，后续研究可以考虑模拟更真实的叶盘工作状态进行测试验证。

5） 整体叶盘切缝后，在缝隙底部会造成较为严重的应力集中，需要优化设计切缝以避免此现象。

6） 进一步优化切缝与切缝填充物，以优化叶盘的多模态阻尼。