基于目标点投影的高炮着发射击毁歼概率计算方法

王亮宽，唐旭，范平，范继，陈晨

(西北机电工程研究所，陕西 咸阳 712099)

高炮毁歼概率计算是非常重要的,是高炮武器系统性能的重要指标之一,对武器装备研制、设计定型试验以及武器系统作战效能评估等具有重要意义。常用的着发射击毁歼概率计算方法是将目标各截面面积沿相对速度方向在炮目垂面进行投影,进而确定命中面积和命中区域,然后结合目标易损性在命中区域内计算毁歼概率[1-5]。GJBz 20499—1998中的着发射击毁歼概率计算方法[6]是将目标近似为规则体且通过毁歼目标所需平均命中弹数计算毁歼概率,由于目标的不规则性和目标部件易损性差异,该方法求得的毁歼概率与实际值存在较大误差。史海龙等[7]提出基于误差投影的高炮毁歼概率计算方法,该方法将炮目垂面上的距离误差投影为目标3个截面所在平面上距离误差计算目标的毁歼概率。由于目标3个截面区域通常是不规则的,将距离误差投影到3个截面判断是否命中目标仍然比较复杂且不易于计算。因此,研究精度高、计算简便的毁歼概率计算方法是非常有必要的。

笔者提出了基于目标点投影的着发射击高炮毁歼概率计算方法,该方法将目标三维轮廓点投影在弹目交汇面,按照目标各部件易损性差异划分投影区域,然后利用蒙特卡罗法依次计算弹丸落在各个区域内的概率,最后根据弹丸对目标各部件的毁歼概率得到高炮一次点射对目标的毁歼概率。该方法能够有效提升毁歼概率计算准确度,有利于武器系统定型试验的顺利进行。

1 目标在炮目垂面的投影区域

为了得到目标在炮目垂面的投影,将目标各轮廓点沿相对速度方向在炮目垂面进行投影。弹丸与目标交汇的示意图如图1所示,O为炮口位置,假设弹丸在时刻t命中目标,此时目标位于Mq点,目标的倾斜角为λ,航路角为q,绝对弹道倾斜角为θ,目标高低角为εq。为了描述投影过程,建立如下坐标系[4]:

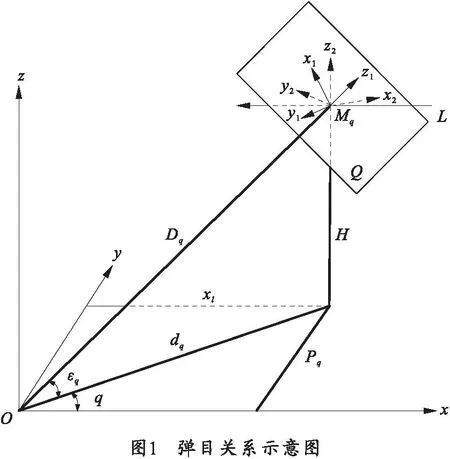
1)大地坐标系O-xyz:以炮口位置O为坐标原点建立大地坐标系O-xyz,其中正北方向为y轴正向,正东方向为x轴正向,垂直向上为z轴方向。

2)Mq-x1y1z1坐标系:以Mq点为原点建立空间直角坐标系Mq-x1y1z1,其中x1轴和y1轴位于过Mq点与炮目连线OMq垂直的平面Q上,x1轴为过炮目连线OMq铅垂面与平面Q的交线,正向朝上;y1轴与x1轴垂直,正向与航路方向同侧;z1轴为OMq的延长线,正向朝远。

3)Mq-x2y2z2坐标系:以Mq点为原点建立空间直角坐标系Mq-x2y2z2,其中x2轴沿水平距离的延长方向,正向朝远;z2轴沿高度方向,正向朝上;y2轴垂直于坐标平面x2Mqz2,正向与目标航向同侧。

记目标提前点Mq在坐标系O-xyz中的坐标为(xq,yq,zq),则从大地坐标系O-xyz到坐标系Mq-x1y1z1的变换关系式为

(1)

从坐标系Mq-x2y2z2到坐标系Mq-x1y1z1的变换关系式为

(2)

在坐标系Mq-x2y2z2中,弹丸的绝对速度矢量Vp和目标的速度矢量Vm为

Vp=(Vpcosθ,0,Vpsinθ),

(3)

Vm=(-Vmcosλcosq,Vmcosλsinq,Vmsinλ),

(4)

式中:Vp为弹丸在Mq点的存速;Vm为目标速度大小。

弹丸相对速度矢量Vxd=Vp-Vm,在坐标系O-xyz中,设弹丸相对速度矢量V′xd=(mxd,nxd,pxd),则有

(5)

设Q′(x,y,z)为平面Q上的任意一点,则可得平面Q的方程为

(x-xq)xq+(y-yq)yq+(z-zq)zq=0,

(6)

式中,平面Q是过目标提前点Mq且垂直于炮目连线OMq的平面。

设P(xp,yp,zp)是目标上的任意一个点,其沿弹丸相对速度矢量方向在平面Q上的投影记为P′(x′p,y′p,z′p),则有

(7)

同理,从目标库读取目标特征数,获取目标三维坐标轮廓,选取N个能够有效表达目标形状的轮廓点。将目标N个点的坐标转换到大地坐标系,然后沿弹丸相对速度矢量方向在平面Q上进行投影,得到N个在平面Q上的投影点。

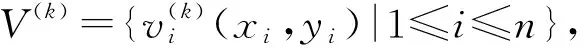
2 毁歼概率计算模型

2.1 毁歼概率计算模型

对着发引信的炮弹,高炮对目标第i个部位一次点射的毁伤概率[4]PKmpni为

(8)

其中:

(9)

式中:m为火炮门数;p为每门火炮身管数;n为一次点射每个身管射弹数;ωi为毁歼目标所需的平均命中弹数(发);ΣⅠ为第一类误差对应的协方差矩阵;xⅡ为第二类误差;ΣⅡ为第二类误差对应的协方差矩阵;AJv为单炮系统误差;A为武器综合体的系统误差;S(i)为目标第i个部位沿相对弹道方向在炮目垂面投影区域的最小凸包。

对着发引信的炮弹,高炮对目标一次点射的毁歼概率PKmpn为

(10)

毁歼概率计算过程中式(8)、(9)需要求解多重积分,多重积分的数值计算方法有均匀网格法和数论网格法等,应用这些方法求解毁歼概率就需要对式(8)、(9)进行一系列的数学变换与简化处理,不仅过程十分繁琐复杂,而且精度也难以保证,因此采用蒙特卡罗法模拟计算。

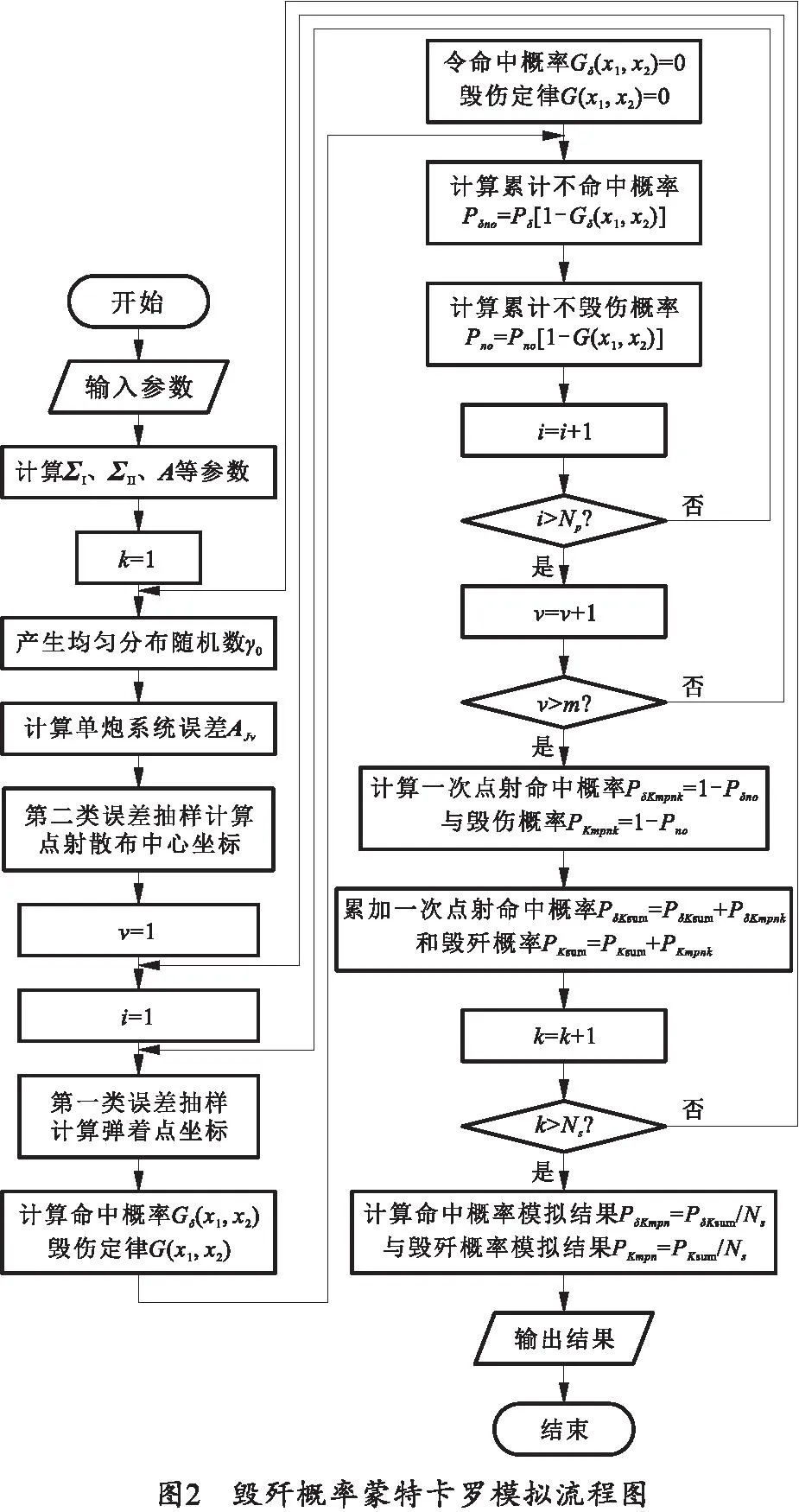
2.2 蒙特卡罗法计算毁歼概率

利用蒙特卡罗法进行模拟计算,记每管发射的射弹数为Np=pn,模拟次数为Ns,模拟计算步骤如下:

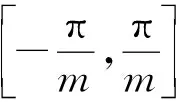
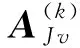
(11)

其中:

(12)

(13)

式中,γv为第v炮的基线矢量与x轴正向的夹角,

(14)

式(12)～(14)其余参数定义可参考文献[4]。

步骤2从标准正态分布N(0,1)抽取随机数ξ1、ξ2,然后计算第k次模拟时的点射散布中心坐标:

(15)

式中:

步骤3开始对第v(v=1,2,…,m)门炮模拟。

步骤4开始对第v门炮的第i(i=1,2,…,Np)发射弹模拟,从标准正态分布N(0,1)抽取随机数ξ1、ξ2,计算第k次模拟时第v门炮的第i发射弹的弹着点坐标:

(16)

式中:

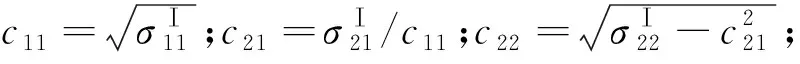
步骤5判断弹着点是否处于目标在弹目交汇面的投影区域,计算弹丸命中概率和毁歼概率:

(17)

(18)

式中:ω为毁伤该部位所需的总弹丸数,其与目标的易损性相关;n=1,2,…,M。

判断弹着点是否位于目标投影区域内可利用PnPoly算法[9]。该算法能够有效判断点与投影区域的位置关系,即通过待测点作一条射线,与投影区域边界交点个数为奇数,则该待测点位于投影区域内部;若与投影区域边界交点个数为偶数,则该待测点位于投影区域外部。

步骤6令i+1⟹i,并进行判断:若i≤Np,转向步骤3;若i>Np,令v+1⟹v并判断:若v≤m,转向步骤2;若v>m,则继续往下执行。

步骤7计算第k次模拟时的一次点射命中概率和毁歼概率:

(19)

(20)

步骤8令k+1⟹k,并进行判断:若k≤Ns,转向步骤1,继续第k+1次模拟;若k>Ns,则结束模拟过程,计算命中概率和毁歼概率的模拟统计值分别为

(21)

(22)

毁歼概率蒙特卡罗模拟流程图如图2所示。

3 实例仿真与分析

根据本文方法和GJBz 20499—1998方法,以正方体、椭球、“战斧”巡航导弹为例,研究一次点射35 mm榴弹对其毁伤效能。笔者采用基于目标点投影的高炮着发射击毁歼概率计算方法,将目标轮廓点投影到弹目交汇面,在投影区域利用蒙特卡罗法进行计算,并采用经典方法将目标投影到弹目交汇面上,再简化为正方形进行计算。笔者在计算时仅考虑击中单个部件,根据目标的实际空间位置,将其划分到靠近弹丸的部件的投影区域内进行毁歼概率的计算,即首先击中的部件。通过仿真计算,比较本文方法和GJBz 20499—1998方法的差异。

3.1 计算条件

假设目标分别是正方体(l=2 m)、椭球体(2.0 m×1.5 m×1.0 m)、“战斧”巡航导弹。“战斧”巡航导弹三维模型图如图3所示,为了计算方便,将“战斧”巡航导弹近似为高6 m、直径0.53 m的圆柱体[10]。

假设各目标均以等速水平直线航路飞行,飞行高度为800 m,航路捷径为500 m,飞行速度为100 m/s。毁歼目标所需的平均命中弹数ω=1.5,点射15发弹。防御系统火炮门数为1门,火炮身管为单管,系统误差为1.0 mrad×1.0 mrad,弱相关随机误差为2 mrad×2 mrad,相关系数r=0.8,强相关误差和不相关误差为0。

3.2 计算结果

当航捷为500 m,高度为800 m,斜距离为2 211 m时,正方体、椭球、“战斧”巡航导弹在弹目交汇面投影及投影面积如图4～6所示。

其中图4～6中(b)图红圈表示目标轮廓点沿相对速度方向在炮目垂面投影区域的凸包特征点,红虚线表示连接投影区域凸包特征点,得到投影区域的凸包进而求解投影区域面积。易知,对大多数目标,投影区域往往是不规则的,而GJBz 20499—1998方法将投影区域近似为正方形区域计算命中概率,这使得命中概率计算结果不够准确[7,11]。若两个部件的投影区域出现重叠时,说明若弹丸穿透能力足够时,则可以贯穿多个部件。

图7分别是正方体、椭球、“战斧”巡航导弹在弹目交汇面投影面积随提前点斜距离的变化情况。由图7可知,相同条件下,本文方法和GJBz 20499—1998方法求得的投影面积存在差异。这是由于本文方法通过将目标轮廓点投影在弹目交汇面,求解投影点集最小凸包的面积,所求面积与实际投影面积误差很小,很接近真实值。而GJBz 20499—1998方法是将目标横截面、纵截面、水平截面面积投影到弹目交汇面求和得到,明显传统方法求得的目标投影面积误差较大。表1、2分别是对不同形状运动目标的命中概率和毁歼概率计算结果。

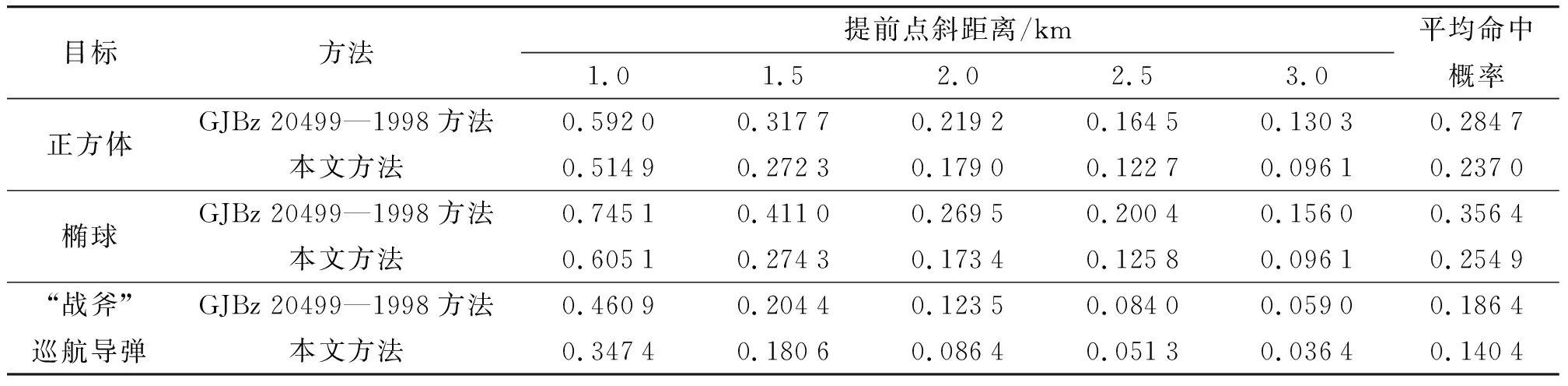
表1 动态目标点射的命中概率

由图7、表1和表2可以看出,当本文方法和GJBz 20499—1998方法计算的投影面积相差较小时,两种方法求得的命中概率和毁歼概率相差不大;反之,两种方法求得的命中概率和毁歼概率相差比较大,通常表现为本文方法比GJBz 20499—1998方法求得的命中概率和毁歼概率都要小,这主要是因为GJBz 20499—1998方法求得目标投影面积过大造成的。

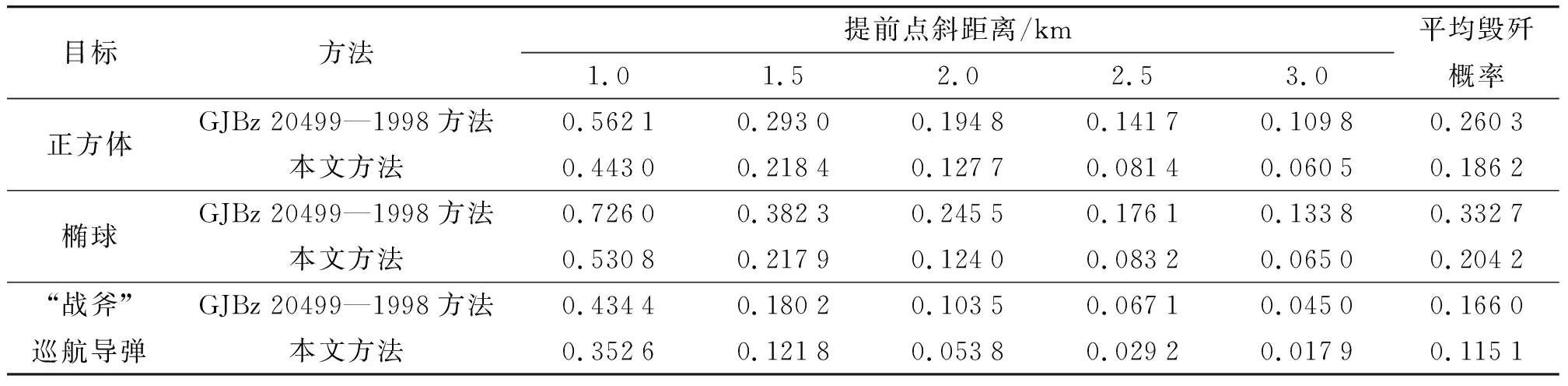
表2 动态目标点射的毁歼概率

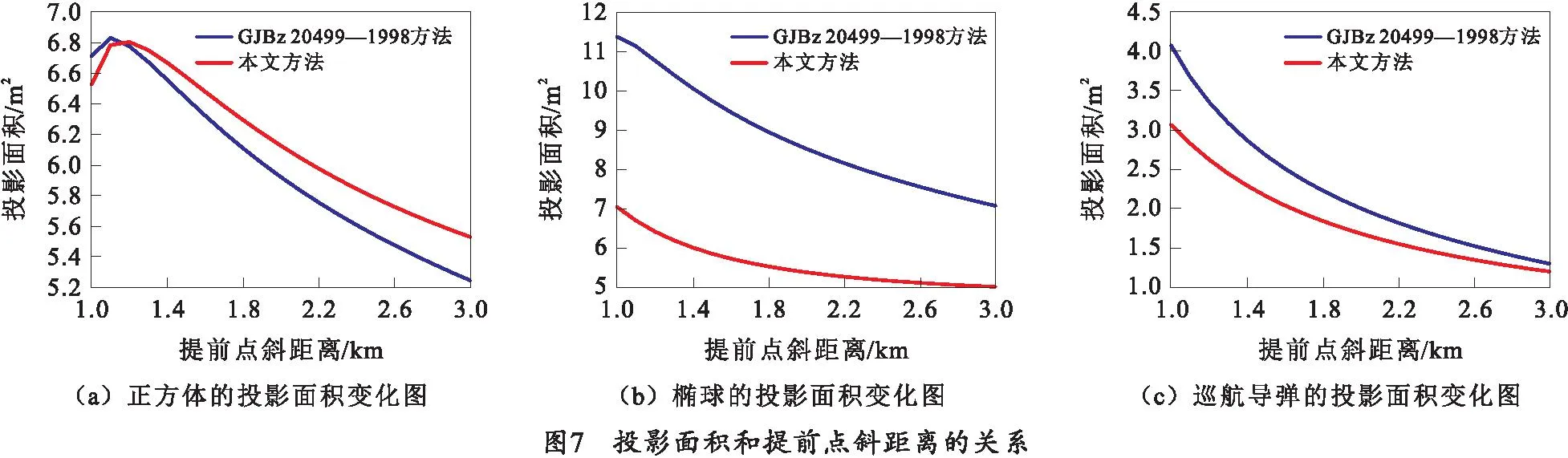
综上所述,投影面积是影响命中概率和毁歼概率计算准确度的重要因素,其与命中概率和毁歼概率呈正相关,当投影面积计算结果偏大时,命中概率和毁歼概率计算结果也会过大,反之亦然。本文方法有效降低了投影面积的计算误差,使得求得的命中概率和毁歼概率更加准确。

4 结束语

笔者采用基于目标点投影的高炮着发射击毁歼概率计算方法,将目标轮廓点投影在弹目交汇面确定投影点的最小凸包,利用蒙特卡罗法模拟每发弹落在投影点最小凸包的概率,进而计算毁歼概率。该方法可很好地减小投影区域计算偏差,特别是形状不规则目标投影区域的计算偏差,能有效提升毁歼概率计算准确度;具有较强的适用性,能够用于各类目标的毁伤效能评估,对武装系统正向研制和定型试验具有重要意义。