弹体侵彻岩石-混凝土复合靶数值分析

韩鸿宇，姚文进，张笑瀛，张小静，徐鹏

(1.南京理工大学 机械工程学院，江苏 南京 210094；2.63863部队，吉林 白城 137001)

现阶段大多数重要设施或军事设施都隐藏于地下几十甚至上百米深或隐蔽于山体中,这些目标大多依托于天然防护材料岩石加以混凝土钢材等人工防护材料,这些材料具有强度较高、抗侵彻性能较好,且具有取材方便、施工工艺简单等特点。为了毁伤这些目标就有必要开展弹体侵彻岩石-混凝土复合介质目标的研究[1-2]。

目前对于弹体侵彻硬目标(岩石、混凝土)常用的研究方法有理论研究方法、实验研究方法和数值仿真研究方法。对于岩石目标而言其侵彻理论远没有混凝土目标侵彻理论成熟[3-5]。根据弹体侵彻岩石目标的实验,对于不同种类的岩石、不同产地但相同种类的岩石其侵彻效应有明显不同[2,6-11]。对于弹体侵彻复合介质目标的侵彻效应由于目标材料力学性能的复杂性,以及复合结构各层介质之间应力波的传播特性复杂性,使得复合介质类坚固目标在侵彻作用下的破坏效应较侵彻单一介质的破坏效应更加复杂[12-14]。笔者将通过数值仿真方法研究弹体侵彻花岗岩-C60混凝土复合介质目标,并分析不同速度与不同靶板倾角(靶板表面与弹轴方向的夹角)下的侵彻规律,为以后进一步研究打下基础。

1 数值仿真模型建立

针对本文研究内容弹体侵彻花岗岩-C60混凝土复合靶建立仿真模型,弹体直径为30 mm,长径比为6,CRH值为4,弹体质量为674.06 g。复合靶由两层介质组成,第1层介质为半径500 mm、高400 mm的花岗岩层,第2层介质为半径500 mm、高300 mm的C60混凝土层。为减小计算量,笔者建立1/2弹靶模型,采用LS-DYNA的Lagrange算法,建立仿真模型。

靶板与弹丸均采用六面体单元进行网格划分,如图1所示。弹体网格大小为2 mm。为了保证计算质量的同时兼顾计算效率,对靶板中心网格加密,加密区网格大小为2 mm并且与周围非加密区之间采用渐变网格,渐变率为1.093 5,即下一个网格长度是前一个网格的1.093 5倍。

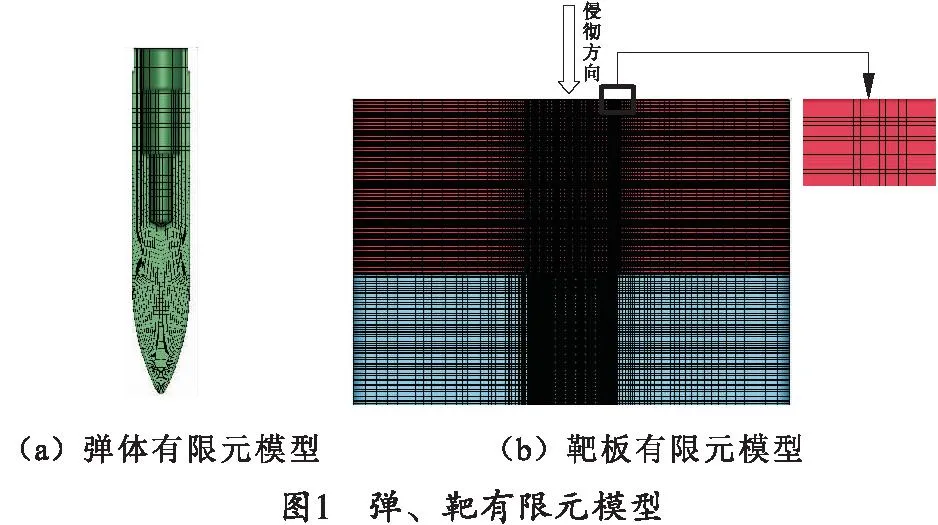
在本文数值仿真计算中,弹体材料为G31采用PLASTIC_KINEMATIC强度模型描述,花岗岩和C60混凝土采用RHT强度模型描述。

PLASTIC_KINEMATIC模型的屈服强度表述为

(1)

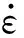
RHT强度模型由德国Ernst Mach研究所的Riedel、Hiermaier和Thoma发展起来的,用于模拟岩石、混凝土等脆性材料在动态加载下的力学行为,较为全面地考虑了材料的压缩损伤、应变硬化以及失效后的应变软化、开裂软化等多种现象,适合计算岩石、混凝土材料的侵彻过程。RHT 模型运用 3 个强度表面界定应力状态,即弹性极限面、失效面与残余强度面。弹性极限面界定了弹性应力状态的范围,随着载荷的不断增大,最后发生屈服或失效。RHT失效面方程为

(2)

弹体材料主要参数如表1所示,花岗岩和C60混凝土材料主要参数如表2所示[2-3,7-8]。

表1 弹体材料PLASTIC_KINEMATIC 模型主要参数

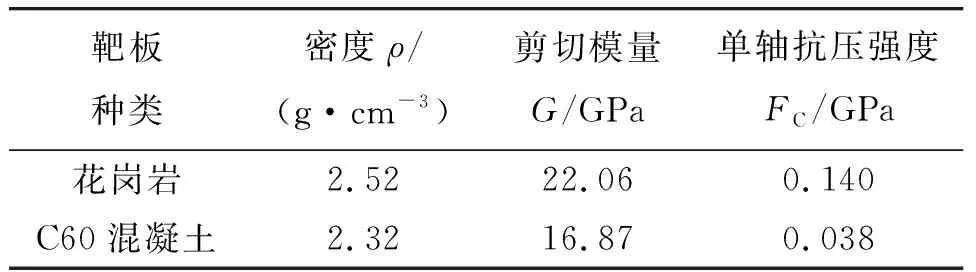
表2 靶板材料RHT模型主要参数

为防止网格畸变而导致数值仿真计算失败,对靶板材料通过添加关键字MAT_ADD_EROSION实现控制单元失效。

2 计算结果及讨论

在数值仿真中,所有的计算工况如表3所示,其中考虑了在不同速度、不同靶板倾角下对侵彻仿真结果进行分析。

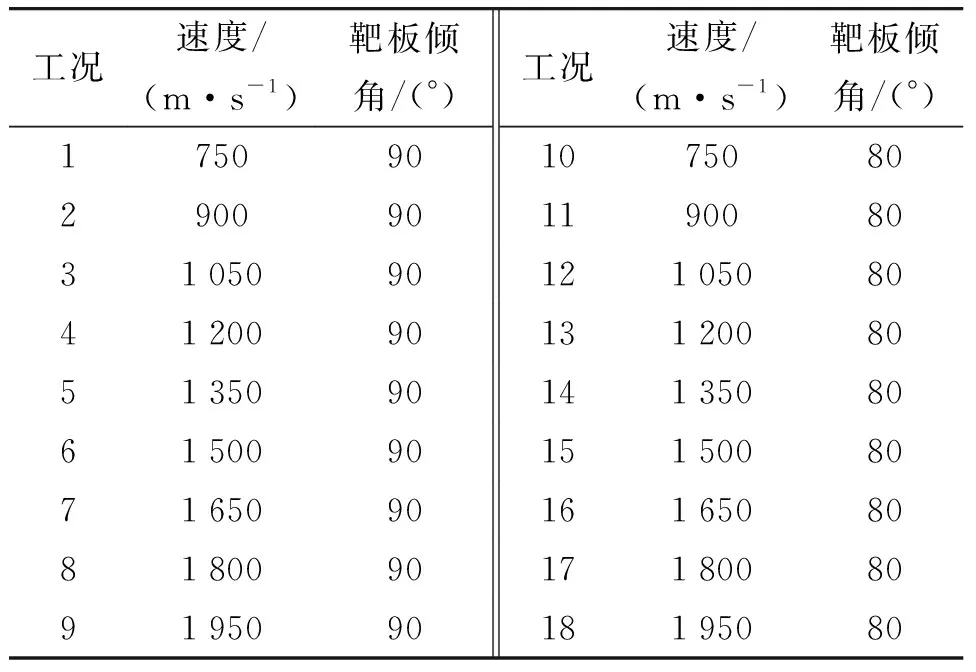
表3 数值仿真工况

2.1 靶板倾角为90°时不同入射速度下的仿真

对应表3中数值仿真工况1～9,在靶板倾角为90°时,考虑弹体以不同速度垂直侵彻复合靶板,其仿真结果如图2所示。

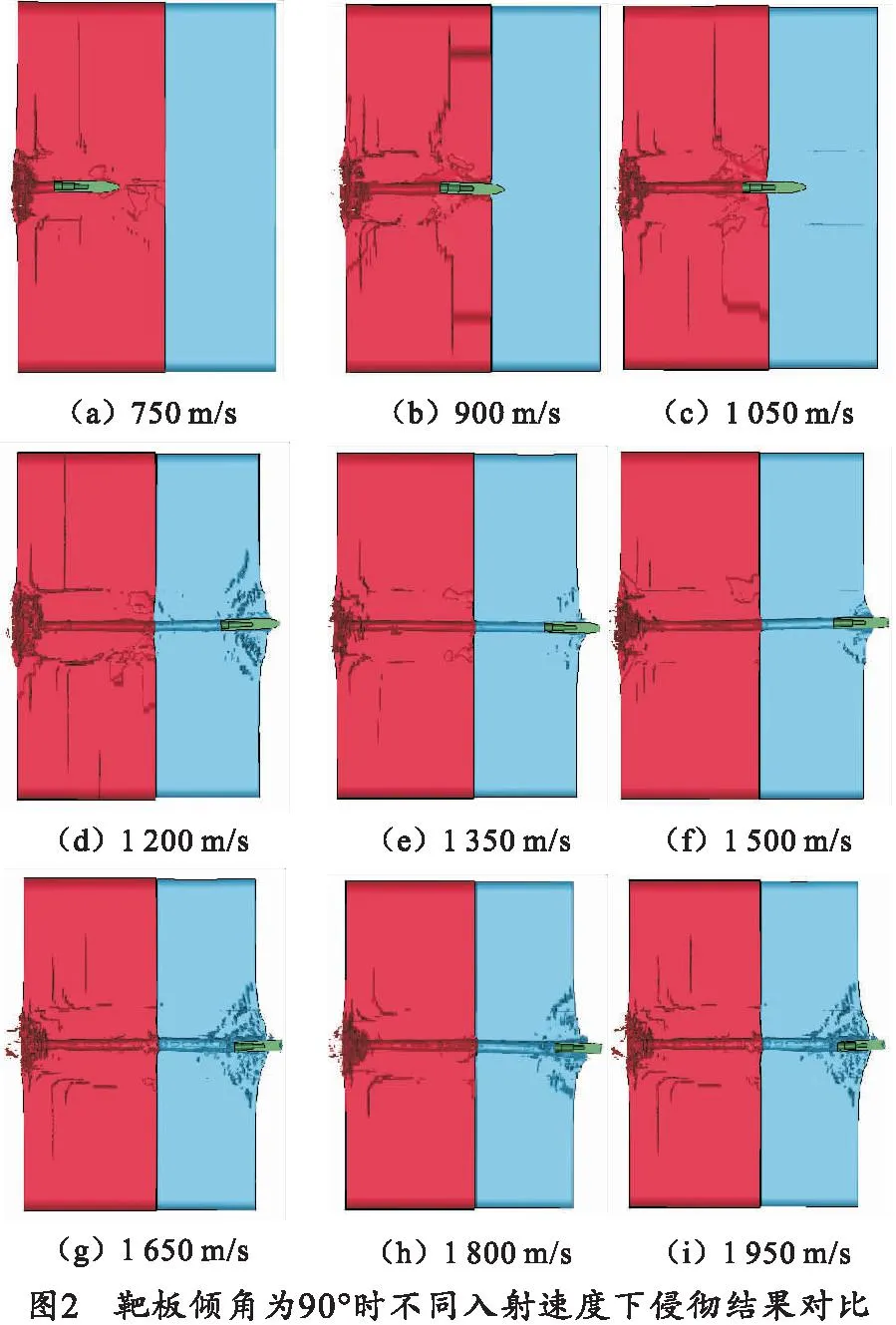
由图2可知,当弹体侵彻到第1层靶后以及第2层靶前没有出现类似侵彻单层中厚靶时剪切冲塞以及重新开坑的现象,即当入射速度低于900 m/s时弹体只对花岗岩层造成有效侵彻,且当入射速度低于900 m/s时弹体外形基本不变。

假定侵彻前、后的弹体质量为M0、MR,则弹体磨蚀率表达式为

(3)

通过式(3)可计算得到弹体磨蚀率,如图3所示。

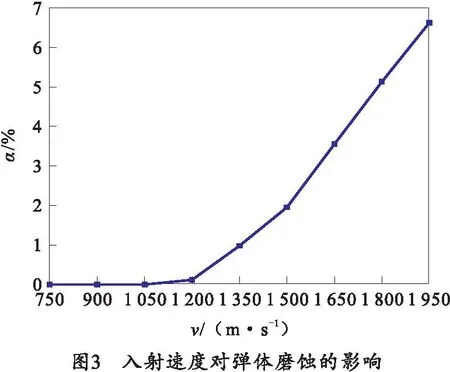
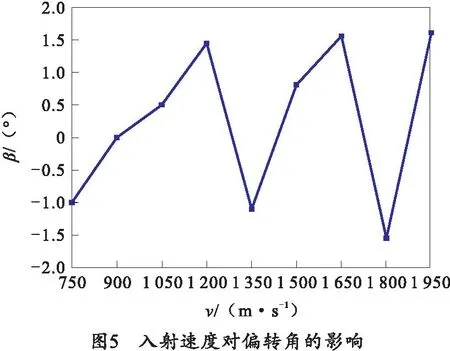
由图3可知弹体磨蚀率α为0,可以将弹体视为刚性。当入射速度为1 200 m/s时弹体头部开始变钝,弹体磨蚀率有所增加但可视为0。当入射速度大于1 200 m/s时弹体头部形状变化大,由卵形弹向平头弹转变,弹体磨蚀率也快速上升,弹体磨蚀率最大达到6.62%。通过仿真结果分析得到入射速度对剩余速度vr以及弹体偏转角β(弹轴方向与水平方向的夹角,逆时针方向为正)的影响,如图4、5所示。

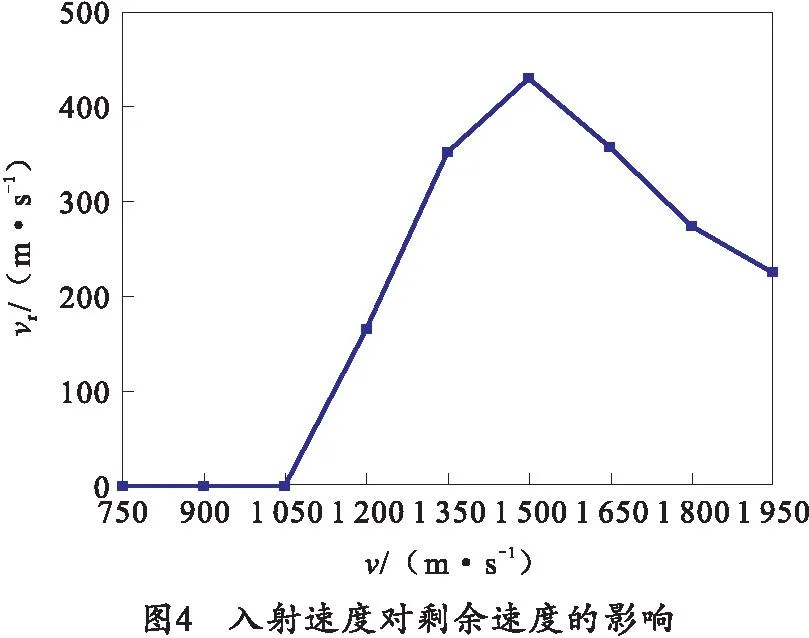
由图4可知,随着入射速度的增加弹体余速vr先增加后减小,这是因为随着入射速度的增加弹体磨蚀率增加,弹体头部形状变化,导致侵彻阻力增加进而导致弹体侵彻效率降低。由图5可知随入射速度的增加弹体偏转角β在0°上下跳动,可视为垂直侵彻。

2.2 靶板倾角为80°时不同入射速度下的仿真

对应表3中数值仿真工况10～18,在靶板倾角为80°时考虑弹体以不同速度侵彻复合靶板,其仿真结果如图6所示。

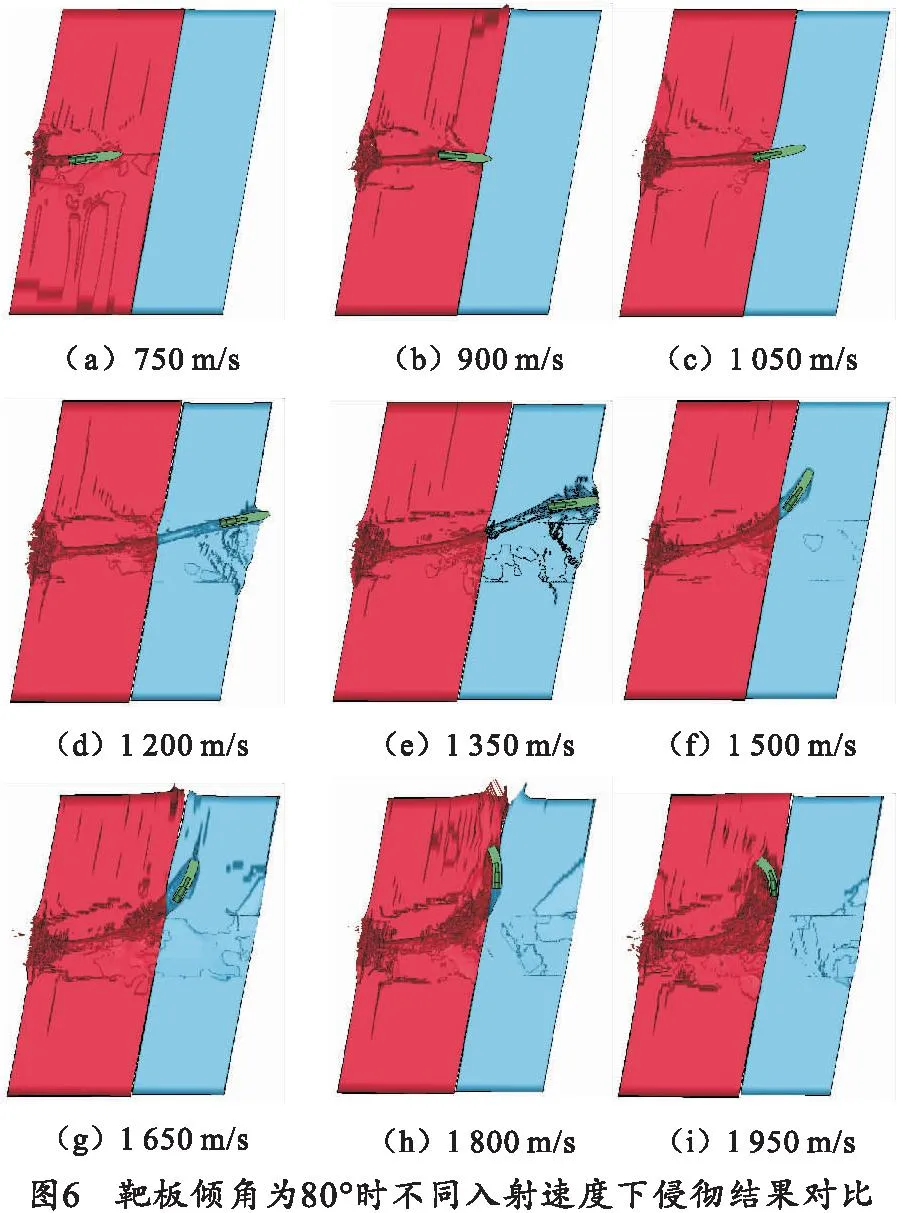
通过式(3)计算得到的弹体磨蚀率如图7所示。由图6、7可知,弹体磨蚀率和弹体头部变形与工况1～9的结果类似,但工况18的弹体磨蚀率较工况9的弹体磨蚀率有所下降。其原因是在侵彻第1层靶板时弹体弯曲导致弹体下侧与靶板的接触面积增加,使弹体下侧所受阻力大于弹体上侧,进而导致弹体偏转角增大使弹体头部未能有效侵彻第2层靶板,减小了弹体磨蚀。通过仿真结果分析得到入射速度对剩余速度vr以及弹体偏转角β的影响,如图8、9所示。由图8可知弹体余速随入射速度的增加先增大后减小。当入射速度为1 500 m/s时弹体余速为0,弹体无法穿透第2层靶板且弹体头部有少量弯曲;当入射速度大于1 800 m/s时,弹体弯曲严重且不能对第2层靶板产生有效侵彻,出现了类似“跳弹”的现象。对比2.1节结果可得,随靶板倾角的减小,余速大幅降低。由图9可知弹体偏转角随入射速度的增大而增大,且在第2层靶板中的弹体偏转角较第1层靶板中的偏转角有所增大,对比2.1节可知弹体偏转角随靶板倾角的减小而大幅上升。

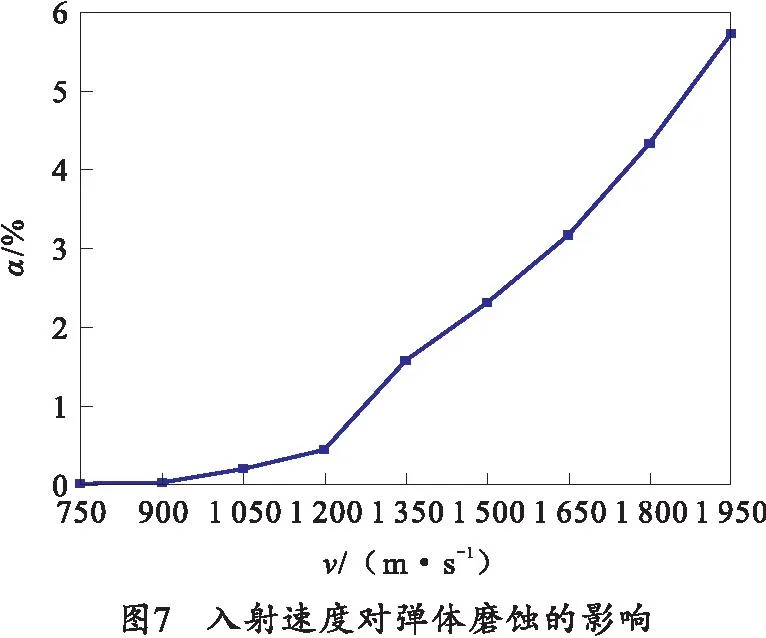
2.3 弹体过载仿真结果分析

选取工况4、13下和工况6、15下的弹体侵彻复合靶板过程进行弹体过载分析,其侵彻结束后的弹体如图10所示。

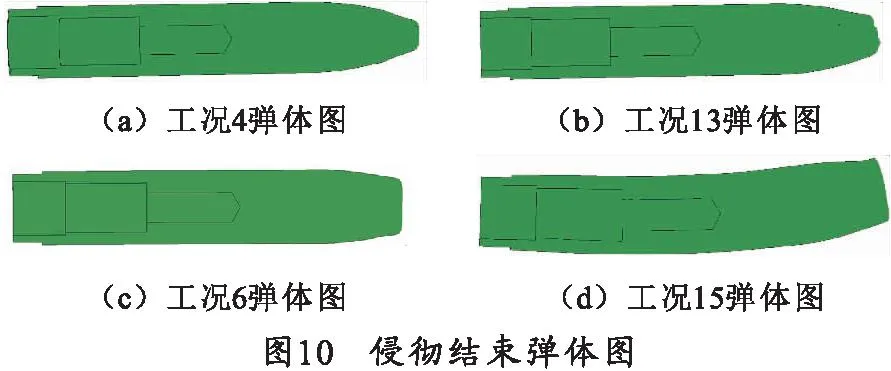
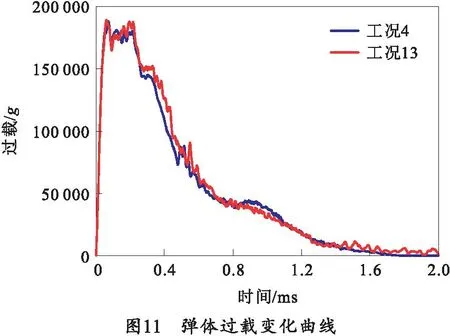
当入射速度为1 200 m/s时,不同靶板倾角下的过载曲线如图11所示。由图11可知工况4和工况13的弹体过载曲线基本吻合。这是因为工况4和工况13的弹体皆穿透靶板,工况13的弹体偏转角不大且侵彻结束后弹体头部形状与工况4相似,弹体没有弯曲。

当入射速度为1 500 m/s时,不同靶板倾角下的过载曲线如图12所示。由图12可知工况6和工况15的弹体过载曲线只在曲线上升阶段吻合,之后,工况6的弹体过载只有小幅上升,而工况15的弹体过载大幅上升。这是因为工况15的弹体偏转角过大导致其弹体头部弯曲,弹体与靶板的接触面积增加导致其侵彻阻力上升即弹体过载上升。

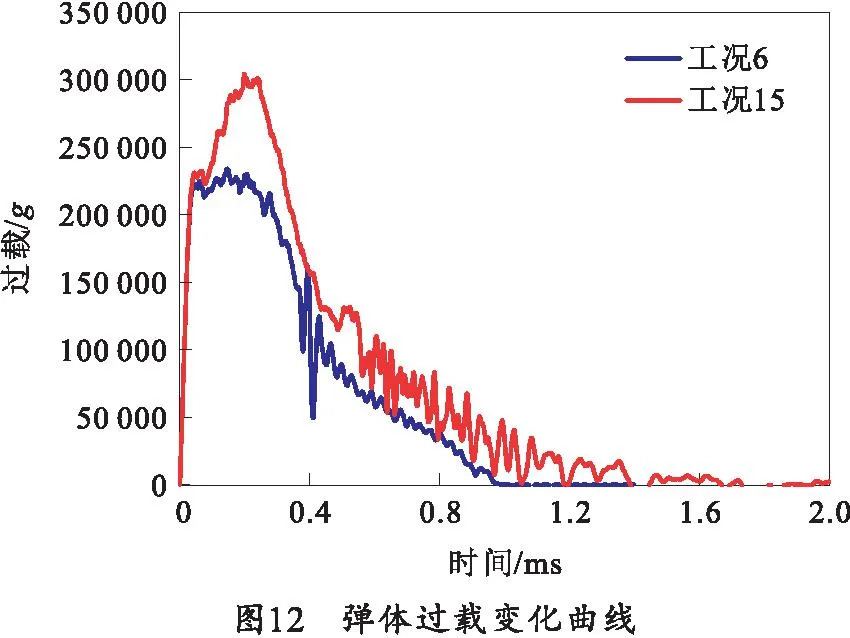
对比图11和图12的过载曲线可知,随入射速度的增加弹体过载也增加,这与动态空腔膨胀理论推导的侵彻阻力相符[15]。侵彻阻力公式为

(4)

式中:d为弹径;fc为靶板无围压压缩强度;ρ为靶体密度;A,B为靶体材料无量纲常数;v为弹体侵彻瞬时速度;N1,N2为弹体头部形状系数。公式包含材料静态强度项AfcN1与动态阻力项Bρv2N2,其中动态阻力项就与速度的二次方相关,由此可知过载随入射速度的增加而增加。

工况6时的弹体过载与质量变化如图13所示,曲线图显示了3个典型时期的弹体形态,由上到下分别为开始侵彻时期,弹体过载最大时期,开始侵彻第2层靶板时期。由图13可知,在工况6状态下,弹体质量在下降时弹体过载还有所上升,其原因可能是弹体质量下降以及弹体头部形状改变导致弹体过载增加大于因速度减小导致的过载减小。弹体过载曲线在开始下降后又上升再振荡下降,其上升阶段即是弹体开始侵彻第2层靶板,后随速度的减小弹体过载逐渐降低直至侵彻结束弹体过载为0。

3 结论

通过一系列数值仿真计算得到了弹体余速、偏转角、磨蚀率和过载曲线,分析了入射速度与靶板倾角对侵彻过程的影响,得到的主要结论如下:

1)当入射速度低于900 m/s时弹体可看作刚性弹体,随入射速度的增加弹体余速先上升后下降,弹体磨蚀率上升,弹体磨蚀主要发生于弹体头部,因磨蚀导致弹体头部形状由卵形弹向平头弹转变。

2)当入射速度一定时,随着靶板倾角的减小,弹体余速下降,弹体偏转角增加且侵彻第2层靶板时偏转角还会加大。随入射速度的增加,弹体将不能穿透第2层靶板还会出现类似“跳弹”现象。

3)当速度低于1 200 m/s时靶板侵彻倾角的改变对弹体过载影响不大,当速度高于1 500 m/s时靶板侵彻倾角的改变会导致弹体过载大幅上升。弹体过载随入射速度的增大而增大,弹体过载随着弹体质量的减小会小幅度上升,且可以通过过载曲线知道弹体何时侵彻第2层靶板。