考虑空化效应的某软后坐火炮制退机液压阻力系数研究

姚蝶，尹强，付佳维，陈龙淼

(南京理工大学 机械工程学院，江苏 南京 210094)

软后坐技术是减小火炮后坐力的有力技术手段,可以明显减小后坐行程,减少炮架受力。与常规后坐火炮不同,软后坐火炮在发射前会先“前冲”一段距离,弹丸发射后会先抵消掉前冲运动所产生的动能再进行后坐[1]。

制退机作为火炮反后坐装置的重要部件,主要结构有节制杆式、筒壁沟槽式、阀控式等多种形式。制退机工作时,活塞挤压工作腔中的制退液来提供后坐阻力。近几年,计算流体力学方法在制退机的研究中应用十分广泛。

节制杆式制退机作为应用最为广泛的制退机类型,吸引了众多学者对其进行研究。陈朝君等[2]针对节制杆式制退机建立了基于实际结构的二维简化模型,通过计算流体力学方法得到了流场的压力、速度和湍动能的瞬时分布。朱锐等[3]修正了前人简化节制环和变直径节制杆的模型,运用动网格技术对制退机内流场进行仿真,得到了与实际情况相符的内部流场瞬态数据,并分析了节制环的磨损机理。除节制杆式制退机外,也有学者对筒壁沟槽式制退机、阀控式制退机等进行了研究,并重点分析了其中液压阻力系数的变化规律。潘孝斌等[4]针对筒壁沟槽式制退机液压阻力系数的影响参数及变化规律进行了研究,结果表明:液压阻力系数随后坐速度、流道面积减小,在一定范围内逐渐增大。史兴亮等[5]通过数值模拟的方法得到了阀控式制退机的液压阻力系数变化规律,通过对动力学模型仿真得到的压力和速度曲线与试验结果基本吻合。林志宸等[6]通过数值模拟的方法得到了某新型阀控式制退机与节制杆式制退机液压阻力系数K的取值范围,并与节制杆式制退机K的经验值对比,验证了该方法的合理性。随着研究的不断深入,空化效应作为后坐过程中一种客观存在的现象逐步进入了学者们的视野。狄长春等[7]基于空化效应对制退机进行了数值模拟,预测了空泡的发生区域,得到了内部腔室压力、速度和气体体积分数的瞬时分布,并计算出液压阻力曲线。丁传俊等[8]基于空化效应对制退机的数值模拟表明:后坐结束时期其非工作腔部分区域充满泡沫化的制退液。除过常规反后坐装置外,梁海彬等[9]针对某软后坐火炮的多通道组合流液孔制退机,提出了一种根据各流液孔的流速关系和流口液压阻力系数求解液压阻力的方法,并通过多前冲速度、多前冲位移仿真得到了前冲机压强损失的规律。

综上可见,对于传统结构的制退机流场研究比较成熟,但针对软后坐火炮制退机的液压阻力系数的研究较少,特别是某新型前冲式制退机中沟槽形式复杂、杆件壁面台阶多、流道多变,开展该型软后坐制退机的液压阻力系数及其与后坐速度相关性研究很有必要。笔者基于计算流体力学方法,在考虑空化效应的情况下,根据该制退机各工作阶段的主流特征,分别在前冲、后坐及复进阶段,建立了带有中心斜孔的筒内壁沟槽主流等效模型、不带中心斜孔的筒内壁沟槽主流等效模型及筒外壁沟槽主流等效模型。采用Mixture多相流模型与标准k-ε湍流模型,研究了不同沟槽深度及运动速度对液压阻力系数K的影响及相应的取值。得到的液压阻力系数随沟槽深度的增大而增大,随速度的增大先减小,达到发生空化的速度后增大。

1 工作原理及流场分析

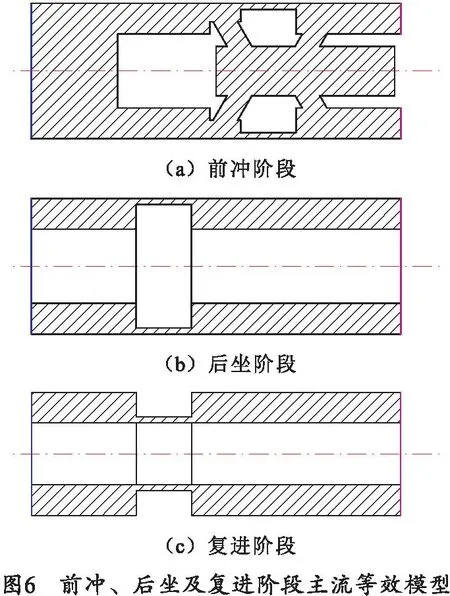
笔者研究的制退机与一般制退机结构不同。在软后坐火炮发射的不同阶段,受运动方向与制退机内部结构相对位置的影响,其流道特征各不相同。前冲阶段制退机内部液体流动情况如图1所示。游动活塞在制退液的推动下,移动至右限位处;制退液通过工作腔经中心斜孔和沟槽两条路径流向非工作腔。

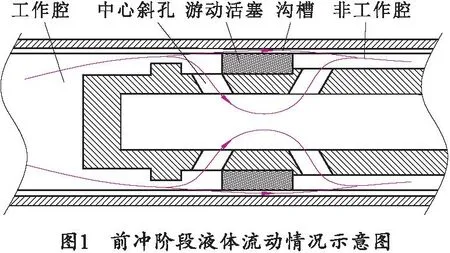
后坐阶段制退机内部液体流动情况如图2所示。游动活塞在制退液的推动下,移动至左限位处;制退液从工作腔仅通过沟槽一条路径流向非工作腔。

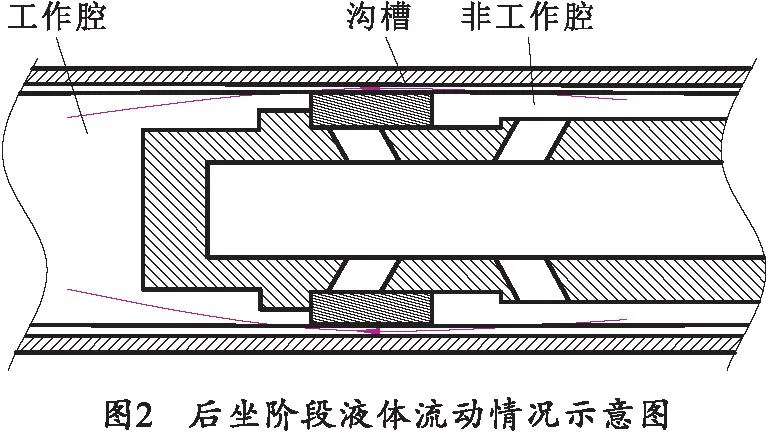
复进阶段制退机内部液体流动情况如图3所示。制退液从工作腔1通过沟槽2流向非工作腔3。

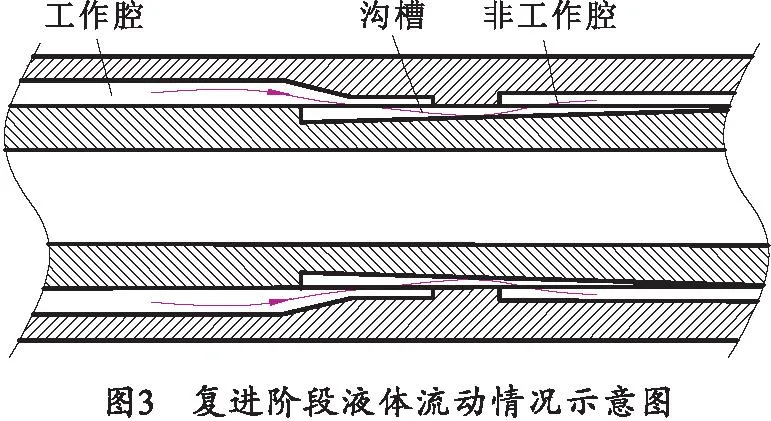
2 液压阻力系数研究

根据该模型引入伯努利方程,有:

(1)

由于制退液在工作腔与非工作腔内的重力势能变化较小,可近似认为相等。再假设工作腔速度为0,非工作腔压力为0,简化式(1)得到:

(2)

由于制退液可认为是不可压缩流体,引入连续性方程:

vgAx=vfax,

(3)

式中:Ax为工作面积;ax为液体从工作腔流入非工作腔时途经最窄处面积。将式(3)带入式(2)可得:

(4)

进一步假设损耗与动能成正比,即:

(5)

将式(5)带入式(4)可得:

(6)

令K=ζ+1,K称为相应流道液压阻力系数,将式(6)变换可得:

(7)

式中,除工作腔压强Pg与工作腔速度vg外,其他均为已知参数。因此在流场仿真时分别设定不同的入流速度,并将仿真得到的压强带入式(7),即可得到相应的液压阻力系数。对于本文涉及的3个模型,公式中的ax与Ax分别根据模型的实际情况选取。其中,前冲阶段的ax为相应沟槽截面积与斜孔横截面积之和;后坐与复进阶段的ax为相应沟槽截面积。

前冲与后坐阶段涉及的沟槽均为内壁沟槽,沟槽截面积计算原理如图4所示,其中L为沟槽宽度,d为沟槽深度,沟槽面积ax=S1+S2=dL+S2。

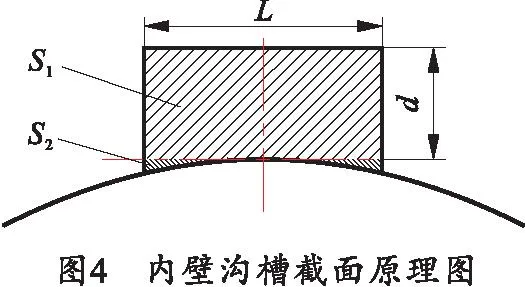
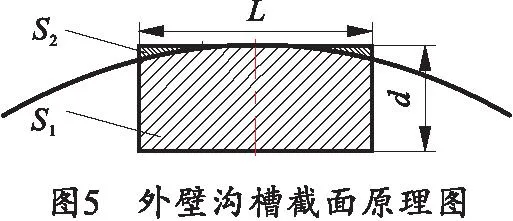
复进阶段涉及沟槽为外壁沟槽,沟槽截面积计算原理如图5所示。其中L为沟槽宽度,d为沟槽深度,沟槽面积ax=S1-S2=dL-S2。

3 模型简化与仿真设置

3.1 模型简化

根据制退机各阶段的液体流动示意图与式(7),可通过流场仿真模拟制退机工作时制退液的流动情况[10-11],进一步计算出液压阻力系数值。

制退机内的流体运动是存在高速射流的三维非定常高雷诺数湍流流动。为降低数值模拟的计算难度,保留制退机工作时内流场的主要运动特征(如工作腔到非工作腔之间,压力、速度发生巨大变化处的结构),对压强、速度变化较小处的结构细节进行简化。此时得到的计算模型合理可靠,同时极大地提高了计算效率。

1)前冲阶段简化为带有中心斜孔的内壁沟槽模型,后坐阶段简化为内壁沟槽模型,复进阶段简化为外壁沟槽模型。

2)考虑到模型的对称性,取二分之一进行计算。

3)模型主要尺寸,特别是沟槽与斜孔尺寸取制退机实际尺寸,其他工作腔与非工作腔的细节尺寸简化处理。

4)工作腔一端端面设置为速度进口,模拟火炮前冲、后坐、复进的速度。非工作腔一端断面设置为压力出口,相对压力为0 MPa,模拟非工作腔被抽真空的压力状况。

根据制退机结构与前冲、后坐及复进时制退液的流动情况,分别建立了如图6所示的主流等效模型。沟槽连接了左端的工作腔与非工作腔。工作腔一端截面为工作面,设置为速度进口边界;非工作腔一端截面设置为压强为0 MPa的压力出口边界。前冲与后坐阶段的沟槽为筒内壁沟槽。前冲阶段的工作腔与非工作腔除沟槽处的连接外,还还原了中心斜孔处的流道结构。复进阶段的沟槽为筒外壁沟槽。

3.2 仿真设置

制退机中,内流场的运动来源于活塞的运动。为了提高计算效率,根据活塞与制退液的相对运动关系,笔者采用稳态仿真代替瞬态求解。前一小节的主流等效模型主要包括了工作腔、非工作腔及沟槽结构。设置工作腔一侧截面为速度进口,进口速度为活塞运动速度;设置非工作腔一侧截面为压强出口,出口压强为0;其余表面设置为壁面。

对3个运动阶段的主流等效模型在不同沟槽深度与进口速度的情况下进行仿真,得到对应的工作腔压强,并计算出液压阻力系数值。仿真利用Fluent中Mixture多相流模型与标准k-ε湍流模型。压力速度场耦合方式采用Coupled。由于制退液中水含量较高,因此在发生空化效应时,第二相可直接设置为水蒸气(water-vapor)。采用分块划分的方法对主流等效模型进行网格划分。由于沟槽处结构较为狭窄,且液流速度很大,流体运动剧烈,故对该处网格进行加密处理。

4 仿真结果与分析

4.1 前冲运动

结合前冲阶段的实际运动情况,将主流等效模型的沟槽深度设置为5.5、4.5、3.5、2.5、1.5、0.5 mm,取进口速度为0.1、0.2、0.5、1、2、4、6、8、10 m/s,对前冲阶段主流等效模型进行仿真,得到工作腔压强。

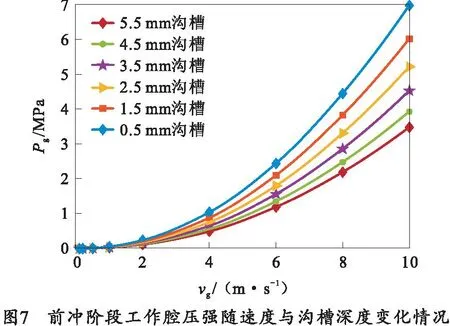
图7所示为前冲阶段工作腔压强随速度与沟槽深度的变化情况,可以看出工作腔压强随前冲速度的增大而增大,随沟槽深度的增大而减小,且在前冲速度小于1 m/s的情况下,工作腔压强的值很小,低于0.1 MPa。

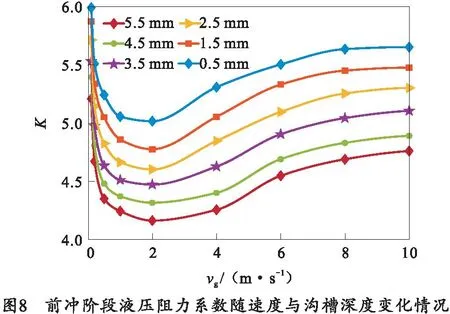
将工作腔压强带入式(7)中可以得到对应前冲速度与沟槽深度的液压阻力系数K。图8所示为前冲阶段液压阻力系数值随速度与沟槽深度的变化情况。可以看出,前冲阶段液压阻力系数范围约在4.2～6.0之间。液压阻力系数在前冲速度小于2 m/s的情况下,随前冲速度的增大而减小;当前冲速度超过2 m/s后,液压阻力系数随前冲速度的增大而增大,且在前冲速度比较大的情况下液压阻力的增长变缓。

该制退机在前冲速度为10 m/s,沟槽深度为5.5 mm时的对称面压力云图、速度云图与制退液体积分数云图如图9～11所示。从图9中可以看出,工作腔压强较大,工作面压强为3.5 MPa;非工作腔的压强较小,压强出口为0 MPa;工作腔和非工作腔两端压强变化较小,工作腔与非工作腔连接处的沟槽与中心斜孔附近压强变化较大。从图10中可以看出工作腔的液流速度较小,在速度进口附近流速为10 m/s,并随着流道截面积的减小而增大,在靠近壁面处的流速几乎为0,在沟槽处达到最大,局部最大速度可达77 m/s,在沟槽及非工作腔形成高速射流,产生了空化效应。空化位置如图11制退液体积分数云图所示。

4.2 后坐运动

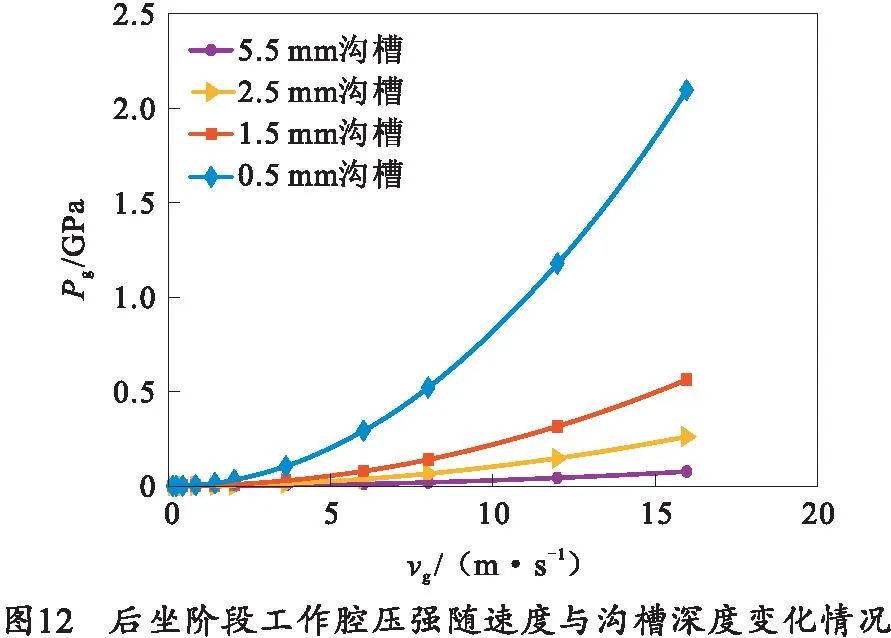
结合后坐阶段的实际运动情况,将主流等效模型的沟槽深度设置为5.5、2.5、1.5、0.5 mm,取进口速度为0.04、0.08、0.2、0.4、0.8、2.0、3.6、6、8、12、16 m/s,对后坐阶段流场模型进行仿真,得到对应的工作腔压强与液压阻力系数分别如图12、13所示。由图12、13可以看出,后坐阶段工作腔压强及液压阻力系数的变化规律和前冲阶段类似。在后坐速度较高的情况下,工作腔压强的数值可以达到1 GPa,液压阻力系数范围约在1.8～2.8之间。

该制退机在后坐速度为16 m/s、沟槽深度为5.5 mm时的对称面压力云图、速度云图与制退液体积分数云图如图14～16所示。可以看出,其压强、速度分布规律与前冲阶段类似,图14～16所示的工作面压强为76.5 MPa,沟槽内局部最大流度可达366 m/s,空化发生于沟槽内侧及非工作腔内。

4.3 复进运动

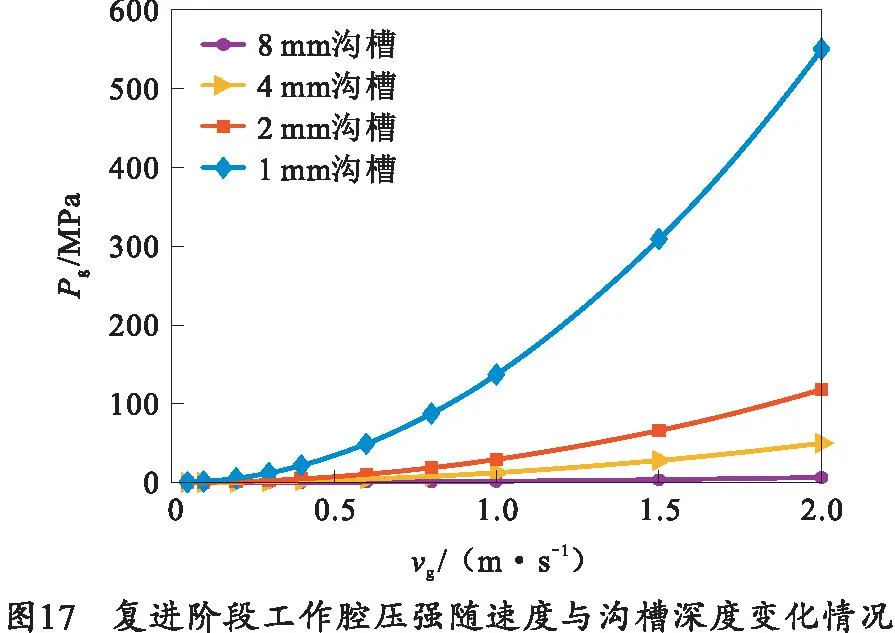
结合复进阶段的实际运动情况,将主流等效模型的沟槽深度设置为8、4、3、2、1 mm,取进口速度为0.05、0.1、0.2、0.3、0.4、0.6、0.8、1.0、1.5、2.0 m/s,对复进阶段主流等效模型进行仿真,得到对应的工作腔压强与液压阻力系数如图17、18所示。可以看出,复进阶段工作腔压强及液压阻力系数的变化规律和前冲、后坐阶段类似。在复进速度较高的情况下,工作腔压强的数值可以达到100 MPa,液压阻力系数范围约在1.6～2.4之间。

该制退机在复进速度为2 m/s、沟槽深度为8 mm时的对称面压力云图、速度云图与制退液体积分数云图如图19～21所示。图中的压强、速度分布规律与前冲、后坐阶段类似,图19～21所示的工作面压强为6.41 MPa,沟槽内局部最大流度可达105 m/s,空化发生于沟槽外侧。

4.4 空化效应

制退机工作时沟槽处液流速度极大,容易发生空化。就本文研究的制退机流场模型而言,笔者在考虑空化效应研究其液压阻力系数之前也进行了不考虑空化效应情况的仿真计算,得到:液压阻力系数随速度的减小而减小;液压阻力系数在速度较小的情况下,随沟槽的增大而减小,但当速度较大时,受空化效应的影响,液压阻力系数随速度与沟槽深度变化关系的规律性较差,且液压阻力的仿真计算结果出现了急剧降低的现象,甚至得到了小于1的计算结果。所以,如果在流场仿真中忽略空化效应,仿真结果中会出现局部过大负压的问题,影响液压阻力系数计算的准确性。

由图8、13和18可以看出,液压阻力系数随速度的变化是先减小后增大的。这是因为在速度较低的情况下没有产生空化现象,而随着速度的增大,到某一值时空化现象产生了。随着速度的继续增大,空化情况变得更加剧烈,液压阻力系数在空化效应的影响下不断变大。而空化的剧烈程度是有限度的,所以到达一定速度后,液压阻力系数随速度的增幅逐渐减小。

图22为截取了后坐阶段3.5 mm沟槽情况下,进口速度为0.4、0.8、1.4、8.0、12.0、16.0 m/s时的二分之一对称面制退液体积分数云图。可以看出,随着速度的增加,在0.4 m/s时没有产生空化效应,从0.8 m/s开始空化现象逐渐增强。结合图13可以看出,随着速度的增大,空化效应逐渐增大。在发生空化前,液压阻力系数随速度的增大而减小,空化效应产生后,液压阻力系数随速度的增大而增大。

5 结论

笔者对应用于某软后坐火炮的新型沟槽式制退机进行了流场仿真分析,对前冲、后坐及复进3个不同的运动阶段建立了等效流场模型,并在Fluent中进行数值模拟。模拟结果得到了该型制退机在不同运动阶段下,不同沟槽深度及运动速度对应的工作腔压强,并通过计算得出了对应液压阻力系数。

1)该型制退机液压阻力系数在前冲阶段范围为4.2～6.0,在后坐阶段范围为1.8～2.8,在复进阶段范围为1.6～2.4。在后续的研究中可使用插值的方法,将该型制退机液压阻力系数带入反后坐装置运动微分方程中,得到准确的火炮后坐部分动力学模型,可为某软后坐火炮的反后坐装置设计及试验测试提供支撑。

2)制退机的液压阻力系数随沟槽深度的增大而减小。在流速较低时,制退机流场没有产生空化效应,这一阶段液压阻力系数随流速的增大而减小,该阶段的趋势和不考虑空化效应的趋势相同;当流速增大到一定值后,沟槽处产生了空化效应,在空化效应的影响下,液压阻力系数随速度的增大而增大,这一段与不考虑空化效应的趋势相反。总体来说,制退机液压阻力系数随流速的增大先减小后增大。