半二面体群上的三度连通边传递双凯莱图分类

曹建基, 王俊新,, 张咪咪

(1.山西财经大学应用数学学院，太原 030006; 2.河北师范大学数学科学学院，石家庄 050024)

0 引言

图的对称性研究是代数图论领域的重要研究课题之一，在编码、密码、计算机网络设计等领域有着广泛的应用。本文将讨论一类三度边传递双凯莱图，考虑其分类。

本文所考虑的群都为有限群，所有的图都为有限、连通、简单无向图。设Γ=(V,E)为一个图，其中顶点集为V，边集为E。Aut(Γ)表示图Γ的全自同构群。若Aut(Γ)作用在集合V(Γ)、E(Γ)和A(Γ)上传递，那么分别称图Γ为点传递图、边传递图和弧传递图。设G为集合Ω上的置换群，且设α ∈Ω。记Gα为α在G中的点稳定化子，即群G中保持α不变的元素生成的子群。称G在集合Ω上作用半正则，如果对任意的α ∈Ω，都有Gα= 1。如果G在集合Ω上作用传递且半正则，那么称G作用正则。众所周知，Γ为凯莱图当且仅当它存在一个自同构群作用在Γ的点集上正则[1]。如果图Γ有一个半正则自同构群H，其作用在图Γ的点集上有两个相同长度的轨道，那么称Γ为群H上的双凯莱图。凯莱图通常如下定义：给定一个群G和一个非空子集S，满足S ⊆G{1}且S-1=S。定义群G上的关于S的凯莱图为Cay(G,S)，顶点集为G，边集为{{g,s}|g ∈G,s ∈S}。类似地，双凯莱图如下定义：设H为群。R、L和S为H的子集，满足R-1=R,L-1=L且R ∪L不包含H的单位元。H上的关于三元集合(R,L,S)的双凯莱图记作BiCay(H,R,L,S)，顶点集为H0∪H1，其中H0={h0|h ∈H},H1={h1|h ∈H}，边集为{{h0,g0}|gh-1∈R},{{h1,g1}|gh-1∈L}和{{h0,g1}|gh-1∈S}三者的并集。设Γ=BiCay(H,R,L,S)，对g ∈H，定义Γ的点集上的一个置换R(g)：

则R(H)={R(g)|g ∈H}为Aut(Γ)的一个同构于H的半正则子群，作用在Γ的点集上有两个轨道H0和H1。若R(H)为Aut(Γ)的正规子群，则双凯莱图Γ= BiCay(H,R,L,S)为H上的正规双凯莱图[2]。另外，若|R| =|L| =s，则BiCay(H,R,L,S)被称为s-型双凯莱图。特别地，当|S| = 1 时，双凯莱图Γ= BiCay(H,R,L,S)也被称作H上的1-匹配双凯莱图。群论和图论中未提及的符号和术语，参见文献[3–4]。

在双凯莱图的研究中，相当多的研究者关注下面的一个很自然的问题：对给定的群H，分类H上具有特殊对称性的双凯莱图。例如，循环群上的三度点传递(边传递)双凯莱图，在文献[5–6]中给出了完全分类。循环群上的所有四度边传递双凯莱图也在文献[7]中给出了刻画，在文献[8]中给出了内交换p-群上的三度边传递双凯莱图的分类。交换群上的三度点传递双凯莱图的完全分类也在文献[9]中被给出。

受上面结论的启发，在本文中，我们将研究半二面体群上的三度边传递双凯莱图。对任意偶数n ≥2，4n阶半二面体群如下定义

注意到交换群上的三度双凯莱图已经在文献[9]中给出了完全分类，下面设n ≥4。本文中，我们将给出半二面体群上的三度连通边传递双凯莱图的完全分类。

1 预备知识

1.1 双凯莱图的基本性质

在这一部分中，我们设Γ=BiCay(H,R,L,S)为群H上的双凯莱图。下面将给出Γ的一些基本性质。

引理1[2]设Γ=BiCay(H,R,L,S)为群H上的双凯莱图，则下面结论成立：

1)H可由R ∪L ∪S生成；

2) 在图同构的意义下，S可以包含H的单位元1；

3) 对H的任意自同构α，都有BiCay(H,R,L,S)≃BiCay(H,Rα,Lα,Sα)；

4) BiCay(H,R,L,S)≃BiCay(H,L,R,S-1)。

若群H的三个子集R、L、S满足R=R-1,L=L-1且1∈S，则称三元有序组(R,L,S)为群H上的双凯莱图三元组。设(R,L,S)和(R′,L′,S′)为两个群H上的双凯莱三元组。如果存在H的自同构α满足(R′,L′,S′) = (R,L,S)α或(R′,L′,S′) =(L,R,S-1)α，那么称(R,L,S)和(R′,L′,S′)等价，记为(R,L,S)≡(R′,L′,S′)。由引理1 中的3)和4)，可得同一群H上的两个等价的双凯莱三元组决定的双凯莱图定同构。

下面给出几个和双凯莱图的自同构相关的结果。设α是H的一个自同构，x,y,g ∈H，定义V(Γ)=H0∪H1的两个置换

令

引理2[2]设Γ= BiCay(H,R,L,S)是H上的一个连通双凯莱图，那么当I=∅时，NAut(Γ)(R(H))=R(H)⋊F；当I ̸=∅时，NAut(Γ)(R(H))=R(H)〈F,δα,x,y〉，其中δα,x,y ∈I。进一步，对任意δα,x,y ∈I，下面结果成立：

1)〈R(H),δα,x,y〉在V(Γ)上作用传递；

2) 如果α是二阶元且x=y= 1，那么Γ同构于Cay(¯H,R ∪αS)，其中¯H=H⋊〈α〉。

引理3[9]设Γ= BiCay(H,R,L,{1})为群H上的1-匹配双凯莱图，则Aut(Γ)中存在包含R(H)的正则子群的充要条件是存在H的阶至多是2 的自同构α，满足Rα=L。

引理4[10]设Γ=BiCay(H,R,L,S)为群H上的双凯莱图，如果R ∩L ̸=∅或S包含二阶元，那么Γ的围长至多是4。

引理5[10]设Γ=BiCay(H,R,L,S)为群H上的双凯莱图，如果Γ为边传递但不点传递，那么Γ为0-型图。

1.2 三维立方体Q3 的循环覆盖

下面我们介绍图CQ(t,m)。设Q3= F008A 为立方体，如图1 所示。设T为Q3的由边集{ax,ay,az,bw,bz,cz,dy}得到的生成树。

图1 立方体图

设m、t为两个整数，满足1≤t ≤m-1 且(t,m)=1，可得t ∈Z∗m。记t-1为t在Z∗m中的逆元，则图CQ(t,m)有点集V(CQ(t,m))=V(Q3)×Zm和边集

图Γ的s-弧是指Γ的s+1 个顶点构成的有序序列(v0,v1,···,vs-1,vs)，满足{vi-1,vi}∈E(Γ)，其中1≤i ≤s，且vi-1̸=vi+1对1≤i ≤s-1 都成立。特别地，1-弧通常叫作弧。设G为Aut(Γ)的子群，如果对Γ的任意两个s-弧，存在唯一的元素g ∈G，把一个s-弧映射到另一个s-弧，那么群G称为s-弧正则。如果Aut(Γ)为s-弧正则，图Γ被称作s-弧正则。

下面引理给出了立方体Q3的循环覆盖。

1.3 半二面体群的性质

下面给出半二面体群的一些简单性质。

引理7 设SD4n为4n阶半二面体群，则下面结论成立：

1)SD4n=〈a〉∪b〈a〉，其中b〈a〉={ba2i}∪{ba2i+1}, 0≤i ≤n-1。进一步有，集合{ba2i}中每个元素阶均为2，集合{ba2i+1}的每个元素阶均为4；

2) Aut(SD4n)作用在集合{ba2i}和{ba2i+1}均传递，其中0≤i ≤n-1；

3) 如果SD4n=〈x,y〉，那么存在α ∈Aut(SD4n)，把集合{x,y}映射到集合{a,b}、{ba,b}、{ba,a}之一。

证明 由半二面体群的定义容易得到SD4n=〈a〉∪b〈a〉。取bak ∈b〈a〉，其中i ∈Z2n，则有

因为a的阶为2n，所以结论1)成立。

对于结论2)，由直接计算可得

所以存在α ∈Aut(SD4n)，满足α把集合{a,ba2i}映射到集合{a,b}。

类似地，由直接计算可得

存在β ∈Aut(SD4n)，满足β把集合{a,ba2i+1}映射到集合{a,ba}，所以结论2)成立。

对于结论3)，令SD4n=〈x,y〉，由半二面体群的结构得x和y至少有一个元素不在〈a〉中。不失一般性，我们设y/∈〈a〉，如果y的阶为2，那么由结论2)可得，存在α1∈Aut(SD4n)，满足yα1=b。因为〈xα1,b〉 =SD4n，所以xα1=ai或bai，其中i与2n互素。ai、b能生成SD4n，且ai、b和a、b满足相同的定义关系，故一定存在α2∈Aut(SD4n)，满足(ai)α2=a且bα2=b。因此，{x,y}α1α2={a,b}或者{ba,b}。

如果y的阶为4，那么由结论2)得，存在β1∈Aut(SD4n)，满足yβ1=ba。因为〈xβ1,ba〉=SD4n，所以可得xβ1=ai或baai，其中i与2n互素。ai、ba可以生成SD4n，且ai、ba和a、ba满足相同的定义关系，故一定存在β2∈Aut(SD4n)，使得(ai)β2=a且(ba)β2=ba，故{x,y}β1β2={a,ba}或{ba2,ba}。容易验证映射c:ba2能诱导出一个SD4n的自同构满足{b,ba}c={ba2,ba}，故结论3)成立。

1.4 三度边传递图的性质

设Γ为图，且设G ≤Aut(Γ)。如果G作用在图Γ的弧集(边集)上传递，那么Γ被称作G-弧传递(G-边传递)。设Γ为一个G-边传递图，且设N为群G的正规子群。

图Γ的关于子群N的商图ΓN如下定义。点集为N作用在点集V(Γ)上轨道的集合，若存在一条图Γ的边，满足两个顶点分别属于两个不同的轨道，则称这两个轨道相邻(连边)。如果Γ和ΓN度数相同，那么图Γ恰好是ΓN的一个N-覆盖。下面介绍一个引理。

引理8[12]设Γ为三度G-弧传递图，如果NG作用在V(Γ)上至少有两个轨道，那么N作用在V(Γ)上半正则。ΓN为三度弧传递图且G/N是ΓN的一个弧传递子群，Γ是ΓN的正则N-覆盖。

2 主要结论

在此节中，设Γ= BiCay(H,R,L,S)为群H ≃SD4n上的三度连通双凯莱图，其中n ≥4。

引理9 如果Γ为0-型图，那么Γ为凯莱图。

证明 因为Γ为0-型，我们可得R=L=∅。由引理1 的结论1)和结论2)，可设S={1,x,y}且SD4n=〈x,y〉。由引理7 的结论3)，可得S为子集{1,a,b}、{1,ba,b}、{1,a,ba}之一。

结论得证。

若一个图的自同构群包含一个循环半正则子群作用在图的顶点集上有四个轨道，则此图被称为四循环图。所有的三度弧传递四循环图在文献[13]中给出了分类，结论如下。

引理10[13]三度四循环图弧传递，当且仅当它同构于下面图之一：

1) F008A、F020A、F020B、F024A、F028A、F032A、F040A；2) F016A、F048A、F056C、F060A、F080A、F096A、F112B、F120B、F224C、F240C；

3) CQ(t,m)，其中2≤t ≤m-3 且m|(t2+t+1)；

4) CQ(2t-1,2m)，其中2≤t ≤m-1 且m|(4t2-2t+1)。

引理11 设R={b},L={ba2t},S={1,a}，其中t为奇数，3≤t ≤n-3 且n| 2(t2+t+1)，则Γ为立方体F008A 的1-弧正则Zn-覆盖。

显然，K可以由a-1cb、c和ca生成。下面证明a-1cb、c、ca和元素a、b、c满足相同的定义关系。首先，c和ca都为二阶元，直接计算可得

注意到

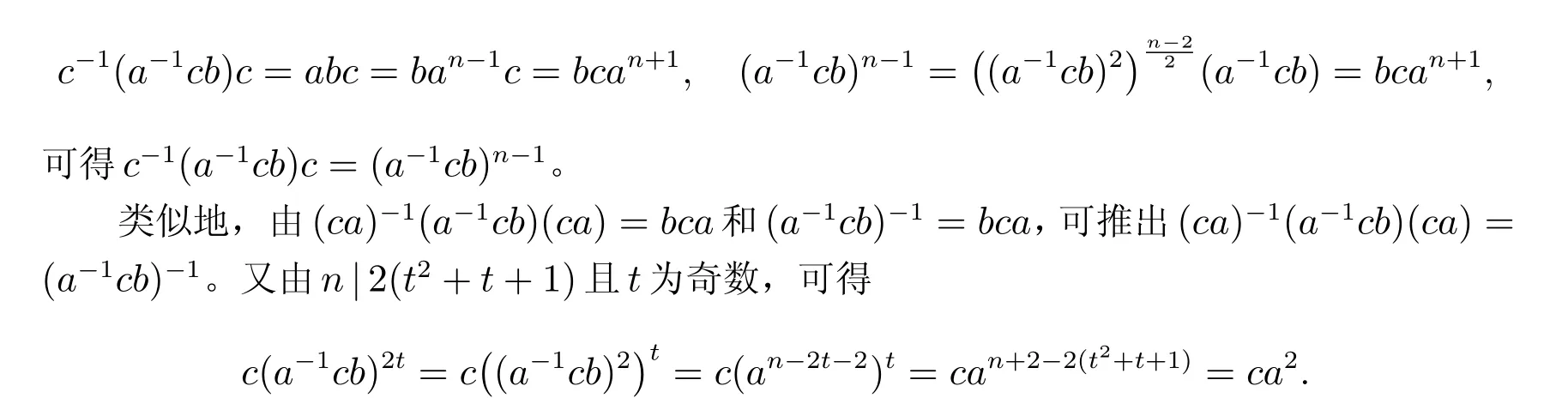
另一方面，(ca)-1c(ca)=a-1ca=c-1a2=ca2，因此(ca)-1c(ca)=c(a-1cb)2t。

因为a-1cb、c、ca与元素a、b、c有相同的定义关系，所以由映射-1cb,,可诱导K的一个自同构β，并且满足bβ=c,cβ=ca, (ca)β=(ca)a-1cb=b，即β为集合{b,c,ca}中元素的循环置换，故β ∈Aut(K,{b,c,ca})，Σ为弧传递。注意到(a2)β=(a-1cb)2=an-2t-2∈〈a2〉，β正规化N=〈R(a2)〉。显然，N ≃Zn在R(K)中正规。因此，NR(K)⋊Aut(K,{b,c,ca})。由引理8 可得商图ΣN同构于立方体F008A，且Σ为F008A 的一个N-覆盖。注意到N ≃Zn，Σ同构于引理6 中结论1)和结论2)中的一个图，容易得到n= 14,t= 9 或t= 11，满足n|2(t2+t+1)且3≤t ≤n-3。另外，n= 14 为满足条件n|2(t2+t+1)且3≤t ≤n-3 的最小值，故Γ至少有112 个顶点。进一步，可得Σ同构于引理6 结论1)中的一个图，故Σ为1-弧正则，引理得证。

引理12 设Γ= BiCay(H,R,L,S)为立方体的N-覆盖，且N ≃Zn对某个n>1，且设图Γ的保簇自同构群作用在Γ上弧传递。如果Γ为1-弧正则，那么NA=Aut(Γ),A/N ≃A4×Z2且N ≤R(H)。进一步有，A中存在包含R(H)的正规正则子群G。

证明 如果Γ为1-弧正则，那么A恰好为Γ的保簇自同构群。由文献[11]，可得A/N≃A4×Z2。设G/N为A/N的Sylow 2-子群，因为A/N ≃A4×Z2，故G/N ≃Z2×Z2×Z2，且G/N为A/N的正规正则子群。因此，G也在V(Γ)上正则。若R(H)N/N不是2-群，则由R(H)∩N为R(H)的循环正规子群，得R(H)∩N ≤〈R(a)〉，故

注意到|〈ai〉|被3 整除，可得R(H)/(R(H)∩N)定包含子群同构于Z3⋊Z2。另一方面，A/N≃((Z2×Z2)⋊Z3)×Z2中没有子群同构于Z3⋊Z2，矛盾。因此，R(H)/N为2-群。进一步，R(H)/N ≤G/N隐含着R(H)≤G。因为R(H)≃SD4n，R(H)的每个Sylow 2-子群同构于〈ai〉⋊〈b〉，其中〈ai〉为〈a〉的Sylow 2-子群，故R(H)/N ≃Z2×Z2。因此，|R(H):R(H)∩N|=4 且|R(H)∩N|=|N|=n。最后，可得N ≤R(H)。

定理1Γ为三度连通边传递图当且仅当双凯莱图的三元有序组(R,L,S)等价于下面情形之一。进一步，可得所有的图均为弧传递。

1)n=4, (R,L,S)≡({b},{ba4},{1,a})且Γ同构于F032A。

2)n=6, (R,L,S)≡({b},{ba2},{1,a})且Γ同构于F048A。

3) (R,L,S)≡({b},{ba2t},{1,a})，其中t为奇数，3≤t ≤n-3 且n|2(t2+t+1)，Γ同构于CQ(t,n)。

4)n=4, (R,L,S)≡({b,ba2},{a,a-1},{1})且Γ同构于F032A。

5)n=10, (R,L,S)≡({b,ba6},{a,a-1},{1})且Γ同构于F080A。

6)n=12, (R,L,S)≡({b,ba2},{a,a-1},{1})且Γ同构于F096A。

证明 由引理11 可得到定理1 的情形3)中图的弧传递性。由文献[14]，我们可以证明定理1 的情形1)∼6)中其余图的弧传递性。

为完成定理证明，只需要证明必要性。容易得到〈R(a)〉为循环半正则子群，且作用在V(Γ)上有四个轨道，故Γ为一个四循环图。由引理5 和引理9，Γ为弧传递，故Γ为引理10 中的一个图。

因为n ≥4，Γ至少有32 个顶点。由文献[15]中主要结论得引理10 中1)和2)中的图除去F008A 外，围长均大于4。如果Γ为引理10 中3)和4)中的图，那么Γ为立方体的1-弧正则覆盖。由文献[11]中主要结论，可得Γ围长至少为6，故Γ围长大于4。

若Γ为0-型图，则R=L=∅。由Γ的连通性得H=〈S〉。因为H ≃SD4n，由引理7 的结论3)，可得S为子集{1,a,b}、{1,ba,b}、{1,a,ba}之一。如果S ̸={1,a,ba}，那么S包含二阶元。由引理4，Γ围长为4，矛盾。设S={1,a,ba}，则Γ中可找到4-圈(10,a1,(ban+2)0,(ba)1)，矛盾。

我们仅需考虑下面两种情形。

情形1Γ为1-型图。

设R={u},L={v}且S={1,w}。因为R=R-1,L=L-1，所以u和v均为二阶元。Γ围长至少为5，由引理4 得u ̸=v且w不是二阶元。令H=〈u,v,w〉，由引理7 中结论2)得，可设u=b,v=an或baj,w=ai或bai，其中j为偶数，i为奇数。如果Γ同构于引理10 中1)和2)中的图，那么n ≤30。由文献[14]得n= 4 且(R,L,S)≡({b},{ba4},{1,a})或者n=6 且(R,L,S)≡({b},{ba2},{1,a})，故Γ同构于定理1 的情形1)和情形2)中的图之一。

如果Γ同构于引理10 中3)和4)中的图，那么Γ为立方体Q3上的1-弧正则N-覆盖，其中N ≃Zn对某个整数n。令A= Aut(Γ)，由引理12，A/N ≃A4×Z2。进一步，A中存在包含R(H)的正规正则子群G，故存在g ∈G，满足1g0= 11。因为R(H)G，由引理2，g=δα,x,y对某个α ∈Aut(H)且x,y ∈H，则

故x= 1。由δα,x,y的定义可得Rα=L,Lα=y-1Ry且Sα=y-1S-1，故uα=v,v=baj对某个偶数j ∈Zn。因此，(R,L,S)≡({b},{baj},{1,ai})或者(R,L,S)≡({b},{baj},{1,bai})。下面，再分两种子情况讨论。

情形1.1S={1,ai}。

由引理12 可知N ≤R(H)。设c为群H的由映射诱导的自同构，易得c为二阶元且满足Rc=L,Lc=R且Sc=S-1。进而，可得δc,1,1为Γ的二阶自同构且K=〈R(H),δc,1,1〉作用在V(Γ)上传递。由N ≤R(H)，得K/N ≃Z32。又因为A/N≃A4×Z2，我们有K/NA/N，即KA，故Γ能看作群K上的正规凯莱图。令

故a2t2=a(n-2-2t)且2t2≡n-2-2t(mod 2n)，所以n|2(t2+t+1)。注意到|Γ| =8n且n为偶数，我们可得Γ同构于引理10 中4)型图。所以Γ ∼= CQ(t,n)，其中t为奇数，且3≤t ≤n-3，故Γ同构于定理1 中情形3)型图。

情形1.2S={1,bai}。

设Γ ≃BiCay(H,{b},{baj},{1,bai})。下面我们再分两种子情形考虑。

情形1.2.1 (i,2n)̸=1。

由(i,2n)̸=1，可得i为奇数且(i,n)̸=1。另外，由Γ的连通性，可得〈a〉=〈ai,aj〉。进一步，可得(i,j)=1，故j ̸=n。我们考虑Γ的距离点11为4 的子图，可得

情形1.2.2 (i,2n)=1。

在此情形下，由映射d:ai a,可诱导出Γ的自同构。Γd ≃BiCay(H,{b},{bak},{1,ba})，其中k为偶数。我们考虑Γ的距离点10为4 的子图，可得

分析Γ4(10)内的点的重合情况，我们得到，如果k ̸≡2,n,n+2(mod 2n)，那么过边{10,11}和{10,(ba)1}有唯一的8-圈(10,11,(ban+1)0,(ban+1)1,(an)0,(an)1,(ba)0,(ba)1)。另一方面，不存在过边{10,b0}的8-圈，与图Γ的边传递性矛盾。下面只需要考虑k ≡2,n,n+2(mod 2n)的情形。

如果k ≡2(mod 2n)，那么Γ ≃BiCay(H,{b},{ba2},{1,ba})。考虑Γ的距离点10为4 的子图，我们可得过边{10,11}和{10,(ba)1}有3 个8-圈(10,11,(ban+1)0,(ban+1)1,(an)0,(an)1, (ba)0,(ba)1), (10, 11, (ban+1)0, (ban+1)1, (an)0, (ban)0, (a-1)1, (ba)1)以及(10, 11,(ban+1)0,(an+1)0,(ban+2)1,(an)1,(ba)0,(ba)1)。另一方面，不存在过边{10,b0}的8-圈，这与图Γ的边传递性矛盾。

如果k ≡n(mod 2n)，那么Γ ≃BiCay(H,{b},{ban},{1,ba})。类似地，考虑Γ的距离点10为4 的子图，可得过边{10,11}和{10,b0}有3 个8-圈(10,11,(ban+1)0,(ban+1)1,(an)0, (an)1,b1,b0), (10, 11, (ban)1, (ban)0, (an)0, (an)1,b1,b0)和(10, 11, (ban)1, (ban)0,(a-1)1,(a-1)0,b1,b0)。另一方面，不存在过边{10,(ba)1}的8-圈，与图Γ的边传递性矛盾。

如果k ≡n+2(mod 2n)，那么Γ ≃BiCay(H,{b},{ban+2},{1,ba})。容易得到Γ的部分图中存在4-圈(10,(ba)1,(an-1)1,b0)，这与Γ的围长大于4 矛盾。

情形2Γ为2-型。

设R={u,v},L={x,y},S={1}，其中u,v,x,y ∈H。注意到，Γ圈长大于4。由引理4，R ∩L=∅。若u、v均为二阶元，则uv ̸=vu。类似地，若x、y均为二阶元，则xy ̸=yx。

由引理7，设R={b,ba2i},L={al,a-l}，其中1≤i,l ≤n- 1。先设Γ为引理10 的1)和2)中的图之一，则n ≤30。由文献[14]可知，n= 4 且(R,L,S)≡({b,ba2},{a,a-1},{1})，或者n= 10 且(R,L,S)≡({b,ba6},{a,a-1},{1})，或者n=12 且(R,L,S)≡({b,ba2},{a,a-1},{1})，故Γ同构于定理1 中情形4)∼6)型图。由引理10，设Γ为立方体F008A 上的1-弧正则N-覆盖，其中N ≃Zn对某个整数n。令A= Aut(Γ)，由引理12 可得A/N ≃A4×Z2。进一步，得N ≤R(H)且A中存在正规正则子群G满足R(H)≤G。因为Γ为2-型图，由引理3，群H有一个阶至多是2 的自同构c满足Rc=L，故R和L由二阶元组成。注意到〈R,L〉̸=H，与群H的结构矛盾。

综合以上几种情形，定理得证。