有限容量多服务员排队系统全忙期分布函数的一种直观计算途径
2024-01-03余玅妙唐建芳
余玅妙, 唐建芳
(1.四川师范大学数学科学学院,成都 610066; 2.四川轻化工大学数学与统计学院,自贡 643000)
0 引言
经典排队系统中,忙期是指顾客到达空闲服务台至服务台再次空闲的这段时间。它在排队模型性能分析中起到了刻画系统运行效率的作用。同时,由于对排队系统忙期的研究有助于人们在实践中高效规划和管理有限的服务资源,因此服务员忙期作为重要的系统绩效指标一直以来受到众多学者的关注。就多服务员队列而言,根据忙期中是否所有服务员都在持续繁忙,还是仅有部分服务员繁忙这两种情况,多服务员队列的忙期有两种不同的定义方式,即部分忙期和全忙期。具体来讲,在具有c个平行同质服务员的排队系统中,部分忙期定义为从发现系统为空的顾客到达开始,到首个使系统彻底变空的顾客离开为止的这段时间。而由Kiefer 和Wolfowitz[1]提出的全忙期概念则被定义为从促使c个服务员中最后一个空闲服务员进入繁忙状态的顾客到达时刻起,到随后c个服务员中的某个服务员变空闲为止的这段时间。在过去的几十年中,针对无限缓冲空间多服务员队列忙期概率密度函数及数字特征的求解涌现出了大量的优秀成果。通过建立反映修正队长演化过程的微分差分方程组,Chaudhry 和Templeton[2]考察了经典M/M/c排队系统忙期的概率密度函数。在此研究的助推下,许多学者先后利用连分式方法、特征函数与矩母函数联合变换方法对多服务员队列的忙期进行了深入的分析,取得了一系列研究成果[3–11]。
另一方面,随着位相型分布理论的蓬勃发展,具有有限容量的马氏排队系统的忙期长度可被视为具有唯一吸收态的Markov 链的吸收时间。因此,首达时间分析方法在过去很长一段时间中被认为是研究该类系统忙期分布的一个有力工具。在众多关于Markov 链理论的学术专著中,也对如何计算有限状态Markov 链的首达吸收态时间分布有着清晰而详尽的阐述[12–14]。但任何研究过度依赖于一种方法未必是一件好事,尤其对工程技术人员而言,他们更乐于接受简洁且通俗易懂的方法。本文正是着眼于上述观点,力图使用Laplace 变换特征根及留数定理,呈现一种分析多服务员有限缓冲队列忙期分布函数的直观方法。值得一提的是,著名排队论专家Chaudhry 教授近期与他的合作者关于顾客等待时间分布函数的研究成果[15–16]给本文带来了诸多有益启示。我们正是利用他们的思路,将研究进一步延伸至M/M/c/K队列中另一重要指标,即服务员全忙期的分析中,为研究复杂多服务员排队系统全忙期分布函数提供了一种易于理解的备选分析方法。
文章整个分析过程将从全忙期分布函数的Laplace-Stieltjes 变换B∗K,c(s)的递推表达式入手;再通过使用上述Laplace-Stieltjes 变换的特征根来获取系统服务员全忙期的分布函数。为便于理解,现简要给出该排队系统的模型描述。本文考虑一个具有c(1≤c<∞)个平行同质服务员的排队系统,他们的服务时间均服从参数为µ的指数分布。顾客以参数为λ的Poisson 流到达,系统中有K(K>c ≥1)个位置可供顾客占用。若到达顾客发现K个位置已全部占用,则自动离开系统不再回来,若有空闲位置则进入服务系统接受服务。进一步,假设模型描述中所涉及到的随机变量均相互独立。
1 全忙期Laplace-Stieltjes 变换的递推公式
本节将利用子全忙期和全忙期之间的一个重要关系来建立全忙期分布函数的Laplace-Stieltjes 变换的简明递推公式。有了这个递推公式,即可通过一些基本的代数运算获得B∗K,c(s)的明确的解析表达式。为证明下述定理,令随机变量Si(i=1,2,···,c)代表顾客在第i个服务员处的服务时间,BK,c(t)表示M/M/c/K队列的全忙期概率分布函数。考虑到数学软件编程计算之需,定理的主要结果以迭代形式呈现并给出初始项B∗c+1,c(s)。
定理1 令Bc+m,c表示有限缓冲M/M/c/c+m排队系统的全忙期(m=1,2,···,Kc)。记分布函数BK,c(t)的Laplace-Stieltjes 变换为
则可使用以下迭代公式计算B∗K,c(s):
证明 在M/M/c/K队列中,当最后一个空闲的服务员进入繁忙状态时,其中某位顾客将在时间χc后结束服务并离开系统,这里χc= min(S1,S2,···,Sc)。在此期间,系统最多允许K-c个顾客进入队列等候。由于全忙期的持续时间与顾客的服务顺序无关,故可假想服务员能够按照自己的意愿选择适当的服务顺序。为分析之需,我们将先到先服务(FCFS)规则更改为后到先服务(LCFS)规则。在这种服务方式下,对全忙期BK,c的分析就会与M/M/c/K-l+1(1≤l ≤K-c)系统全忙期的分析发生重要的关联,这一点将在后文分析中结合图示给出全面阐述。另外,如果在χc期间到达的顾客少于K-c个,那么变空闲的服务员将立即开始为在χc时间内到达的最后一个顾客提供服务。
不失一般性,假设变空闲的繁忙服务员即将开始为第(K-c)位顾客提供服务。如果在这个顾客的服务时间内有更多的服务员由繁忙转为空闲可用,那么他们将为第(K-c)位顾客的所有后代提供服务,直到没有此类后代可供服务为止。这里,第(K-c)位顾客的后代指的是那些可以进入缓冲空间等待,且发现所有c个服务员均在忙碌的顾客(包括后代的后代,即子子孙孙)。我们把完成这些顾客服务所需的时间称为由第(K-c)位顾客产生的子全忙期(注意一个后代的后代所需的服务时间已被计入其中)。当上述子全忙期结束后,一个可用服务员将开始为第(K-c-1)位顾客提供服务,此后若有其他空闲可用服务员出现,他们将为所有在第(K-c-1)位顾客的子全忙期中进入队列的后代提供服务,这里后代的定义与前述完全一致。空闲的可用服务员将一直沿用此服务方式,最终服务完第1 位顾客及其他的所有后代子孙。令DK,c,j(j=0,1,2,···,K-c)表示M/M/c/K队列中由第j位顾客产生的子全忙期的长度,注意在后文分析中,我们取DK,c,0= 0。因此,根据服务时间的独立同分布性质和指数分布的无记忆性,我们将整个全忙期BK,c分解为
其中N(χc)表示在随机时间长度χc内到达系统的顾客数量(包括到达后发现系统已满并因此被阻挡而未能进入队列的顾客),其中H(x)表示Heaviside 阶跃函数,按常规定义
通过考虑在服务时间χc内到达的顾客数量,并使用全期望分解技术,我们可以获得随机变量BK,c的分布函数的Laplace-Stieltjes 变换如下
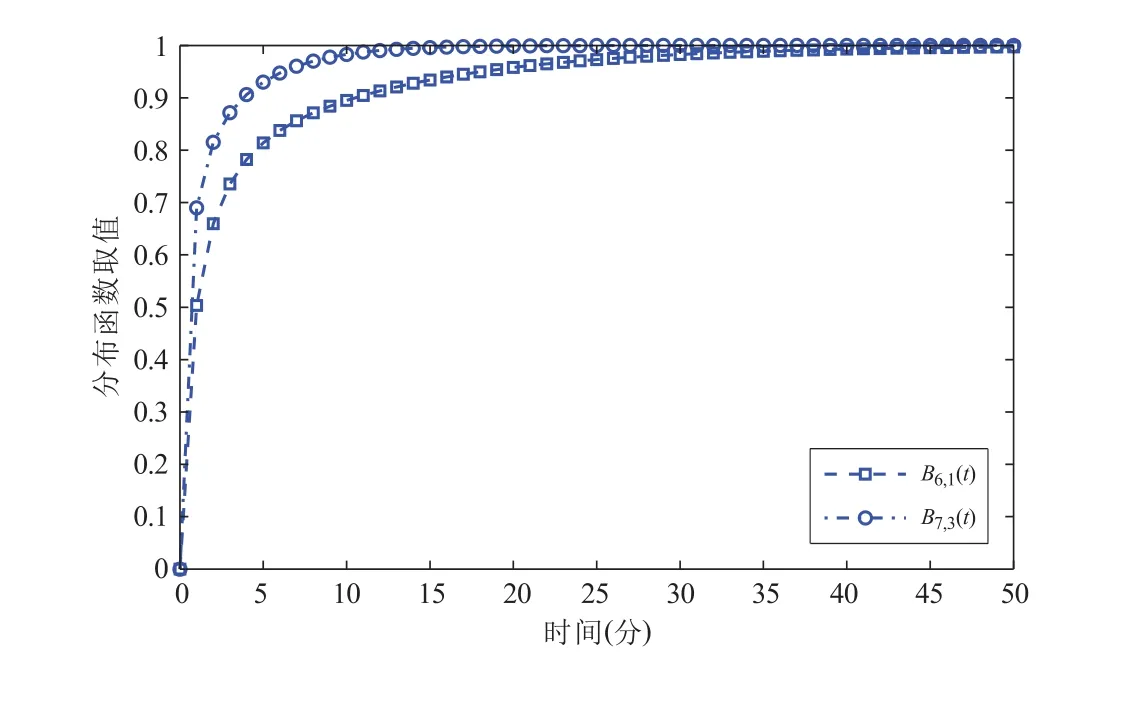
从方程(1)中注意到,为了获得B∗K,c(s)的解析表达,须逐一确定D∗K,c,l(s)(l= 1,2,···,K-c),而以下事实对解决上述问题起着至关重要的作用。如果BL,c(c 这里举一个例子来帮助读者理解这个事实。考虑一个简单的M/M/3/7 排队,并假设在服务时间χ3内有两个顾客加入队列,其中χ3=min(S1,S2,S3)。从图1(a)和图1(b)可以看出,当空闲的服务员开始为第二位顾客和他的后代子孙服务时,第一位顾客总是占据着等待队列的第一个位置。因此,在M/M/3/7 队列中,由第二位顾客产生的子全忙期D7,3,2与M/M/3/6 队列的全忙期B6,3分布完全相同。利用DK,c,l和BK-l+1,c之间的这一关系,方程(1)可以改写成如下适合递推计算的形式 图1 D7,3,2 与B6,3 具有相同概率分布的图示说明 利用Mathematica 软件包强大的符号计算能力,可以迭代给出B∗c+2,c(s)和B∗c+3,c(s),并最终获得B∗K,c(s)的解析表达式。此外,我们还注意到,全忙期分布函数的Laplace-Stieltjes 变换具有有理结构形式,即 其中多项式QL,c(s)的次数总是高于多项式PL,c(s)的次数。这意味着我们可以通过使用部分分式分解技巧和留数计算规则来反演相应的Laplace-Stieltjes 变换,以获得全忙期的概率分布函数。详细的过程将在下一节中呈现。 所谓B∗K,c(s)的特征方程即是多项式方程QK,c(s) = 0。为了从BK,c的Laplace-Stieltjes 变换反演出全忙期分布函数BK,c(t),必须知道特征方程全部的具有负实部的特征根。特征方程QK,c(s) = 0 在复平面上共有K-c+1 个根,在这些根中,我们假定有v个具有负实部的特征根,记作θr, 1≤r ≤v。利用这些特征根,B∗K,c(s)可以通过部分分式分解展开写成如下简洁的表达形式[15,17] 为得到全忙期的概率密度函数bK,c(t),对方程(4)实施Laplace 逆变换后,有 这里δ(t)表示Dirac 单位脉冲函数。关于Laplace 逆变换的更多细节,请参考文献[18]。因此,根据方程(5),全忙期的概率分布函数可以最终表示为 进一步,利用复分析中极点处的留数计算公式,并注意到B∗K,c(s)|s=0= 1,则上述方程(6)中出现的未知常数b0,b1,b2,···,bv可由 加以确定,其中Q′K,c(θr)为多项式函数QK,c(s)在s=θr处的导数。这里可根据方程(7)的第二分支事先求出b1,b2,···,bv,然后再利用上述结果求出未知常数b0。将方程(7)中b0的值代入方程(6),即有 如上述分析过程所呈现的那样,我们实质上假设了θr(r= 1,2,···,v)是一系列互异的特征根。如果上述具有负实部的特征根中出现重根的情况,则只需对推导过程稍作修正即可得到该情形下对应的全忙期分布函数[17]。事实上,Tijms[19]和Chaudhry 等人[20]均指出在排队分析的绝大多数情况下,根方法所依赖的根都具有良好的结构分布,且均为互异的单根。本文受限于篇幅,且考虑到重根情形在实际分析计算中少有发生,因此我们省略了对重根情形的详细讨论。 本节提供一些典型的数值算例来说明前两节所得公式的适用性。所有的数值计算均借助于Mathematica 软件包在一台配置为Corei7 处理器、频率为2.6 千兆赫、16 千兆字节DDR3 内存的个人电脑上进行。下面第一个数值算例的目的是验证前述理论分析结果的正确性。 例1 令c= 1,本文模型退化为Takagi 和Tarabia[21]研究的M/M/1/K队列。此时所谓的全忙期变为单服务员队列的经典忙期,Takagi 和Tarabia 在上述工作中报道了服务员忙期长度的一阶原点矩为来计算,因此在相同的系统参数下,由方程(9)得到的计算结果应与由方程(10)得到的计算结果完全一致。这也是调试计算程序,检查计算准确度的一种有效方法。考虑一个M/M/1/6 排队系统,设定系统参数µ= 1,λ= 0.8,并由此导出ρ= 0.8。将上述参数代入方程(9)中,可得E[BK,1] = 3.689 280。另一方面,定理1 中的迭代公式促使我们能够获得如下的关于B∗6,1(s)的解析表示 利用Mathematica 软件求解上式的特征方程,数值结果表明 将B6,1(t)代入方程(10)中,仍然可得E[BK,1] = 3.689 280。这从一个侧面证明了本文理论分析的正确性。 例2 接下来,考虑一个一般的多服务员队列,设系统参数取值为λ= 1.5,µ= 0.7,c=3,K=7。那么全忙期B7,3的Laplace-Stieltjes 变换由 同样,将这些值代入方程(8),得到相应的系数 从而可由方程(8)最终获得分布函数B7,3(t)的表达式如下 为更加直观地体现数值计算结果,图2 中分别给出了M/M/1/6 队列和M/M/3/7 队列的全忙期分布函数的图像。 图2 M/M/1/6 队列和M/M/3/7 队列的全忙期分布函数图像 本文提出了一种较为直观的方法来计算有限容量多服务员队列中的全忙期分布函数BK,c(t)。不言而喻,找到分布函数将有助于我们更加全面地掌握随机变量BK,c中包含的各种概率统计信息。本文所提出的方法简单易懂,也很容易通过数学软件编程计算求得其具体的数值结果。整个分析方法主要基于全忙期分布函数的Laplace-Stieltjes 变换递推式以及该变换所对应的特征方程的负实部特征根,这两者均可使用成熟的数学软件包Mathematica 或Maple 轻松方便地求取。 作为本文研究内容的扩展,我们认为文中所呈现的分析技术也可以推广用来考察离散时间队列和非马氏队列的忙期分布,这些内容将有待于我们在今后的研究中加以解决。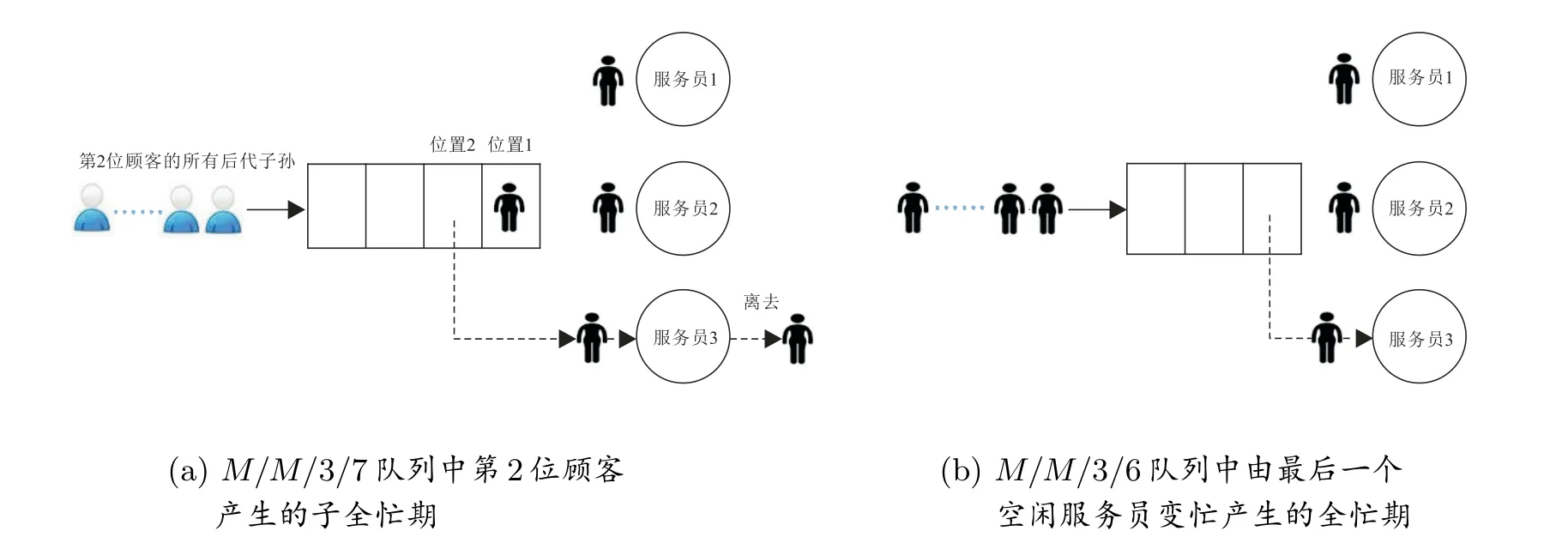

2 全忙期分布函数
3 算例展示


4 结论
