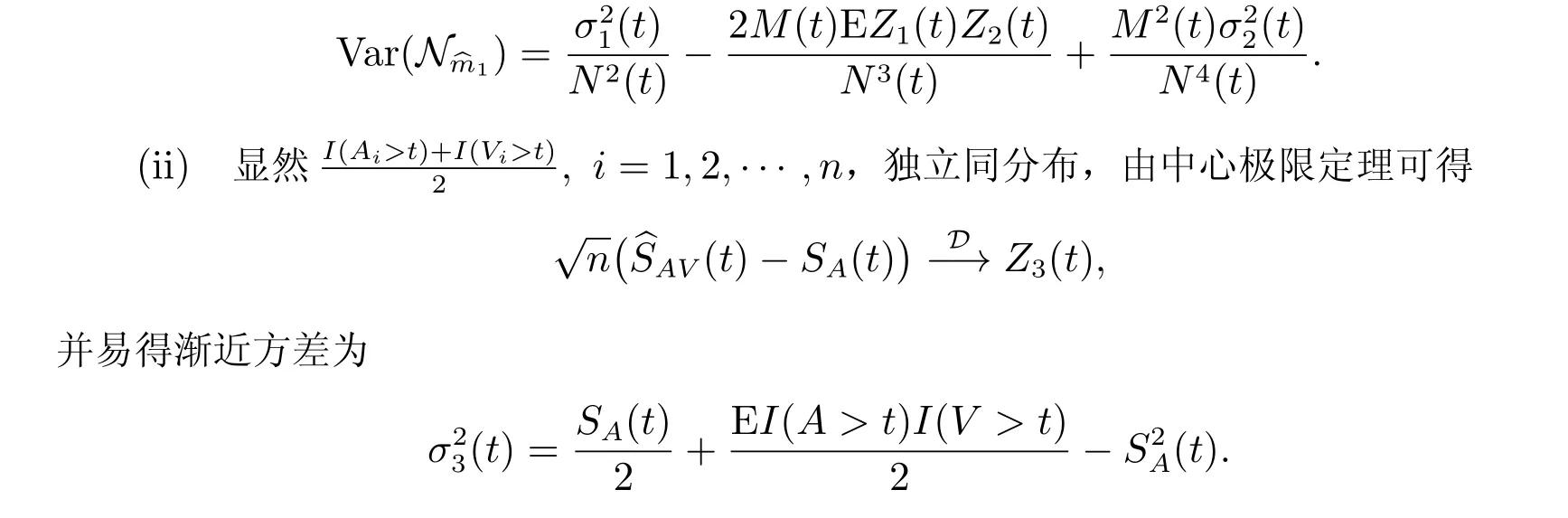长度偏差完全数据下均值剩余寿命的矩类估计

2024-01-03武洪萍

工程数学学报 2023年6期

武洪萍

(山东石油化工学院大数据与基础科学学院，东营 257061)

0 引言

均值剩余寿命又称为期望寿命，是指系统或个体在已生存时间t后还能继续生存的寿命期望。这一概念在生物医学等诸多实践领域中发挥着重要作用。目前，关于均值剩余寿命的统计推断已经出现了很多研究结果。例如，Yang[1]在完全样本下提出了均值剩余寿命的非参数点估计；当寿命数据为右删失时，Kumazawa[2]提出了均值剩余寿命的一致估计；对于左截断右删失样本，Zhao 等[3]以生存函数的左截断乘积限估计为基础，发展了均值剩余寿命的非参数估计；而Wu 和Shan[4]则在长度偏差右删失样本下研究了均值剩余寿命的矩类估计。另外，对于长度偏差完全样本，Fakoor[5]以感兴趣总体分布函数的经验估计为基础，发展了均值剩余寿命的经验估计。类似于文献[5]中的研究工作，本文将主要致力于研究长度偏差完全样本下均值剩余寿命的矩类估计。

长度偏差数据就是平稳性假设前提下的左截断数据，这也就意味着在长度偏差数据中个体对应的生存时间被纳入样本的概率与它的长度成正比。已有文献中除了对长度偏差数据进行描述之外，也讨论了其统计推断。例如，Luo 和Tsai[6]提出了生存函数的两种伪部分似然点估计，但是这种伪似然方法处理起来比较困难。因此，Huang 和Qin[7]在长度偏差右删失样本下对左截断P-L 估计[8]进行了改进，得到了生存函数的乘积限类估计。另外，为了在删失长度偏差数据下估计分位数剩余寿命，Wang 等[9]提出了以模型为基础的非参数和半参数估计方法，并将它们用于分析痴呆症患者的分位数剩余寿命。Shi 等[10]则在删失长度偏差数据下分析了分位数的非参数估计。对于有协变量出现的半参数模型，也已出现很多的研究结果。例如，为了分析Cox 模型中的参数效应，Qin 和Shen[11]及Huang 和Qin[12]分别在长度偏差数据下提出了模型的矩法估计方程和复合估计方程；而Bai 等[13]和Wu 等[14]则分别研究了比例均值剩余寿命模型和加性均值剩余寿命模型的估计方程。

长度偏差数据在寿命研究广泛存在，但是在长度偏差完全样本下对均值剩余寿命的研究却很少。因此，本文重点研究均值剩余寿命在长度偏差完全数据下的非参数估计及其渐近性质。在估计过程中，利用目标总体和长度偏差变量之间的关系，通过消除均值剩余寿命函数中总体均值这一冗余参数的影响，建立目标参数的矩类估计。同时，也证明了估计量的大样本性质，并通过数值模拟研究其在有限样本下的性质。

1 符号假设

设T0表示某感兴趣系统或个体的寿命长度，而A0为作用于T0的左截断时间，两者非负且独立。在左截断抽样机制中，当且仅当A0≤T0时，个体的寿命长度才能被观测到。因此，为保证部分个体的寿命长度是可以被观测的，需假定左截断概率α= Pr(A0≤T0)> 0。令A和T分别表示可观测的左截断时间和寿命长度，则可观测数据对(A,T)的概率分布与(A0,T0)在给定条件A0≤T0时的条件概率分布相同。若A0的概率分布为均匀分布，那么在左截断抽样下得到的可观测变量T是一个长度偏差变量。

而长度偏差变量T的密度函数为

由(1)式，可得

同样，可得A和V享有相同的概率密度，即

根据均值剩余寿命函数的定义，感兴趣生存时间T0在给定时刻t ∈[0,τ)的均值剩余寿命为

或

当t ≥τ时，m(t)=0。

2 估计方法

不妨设(Ai,Ti),i=1,2,···,n，是来自(A,T)的一个简单随机样本。Fakoor[5]在(1)式基础上将T0的分布函数F表达为

而当t ≥T(n)时，︿mn(t)=0。

显然，在上述估计过程中，没有考虑消除冗余参数µ的影响。为此，我们提出m(t)在长度偏差完全数据下的另外两种非参数估计。

2.1 估计方法I

结合(1)式和(4)式，随机变量T0在给定时刻t ∈[0,τ)的均值剩余寿命可以表示为

这里0≤t

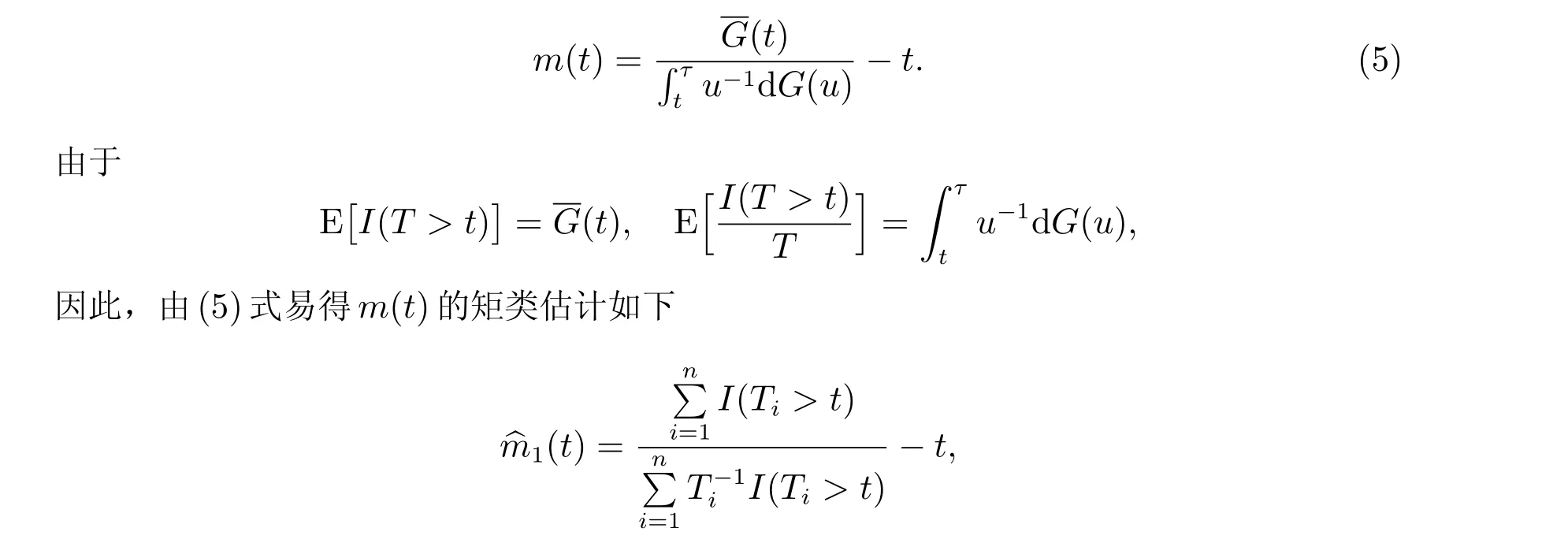
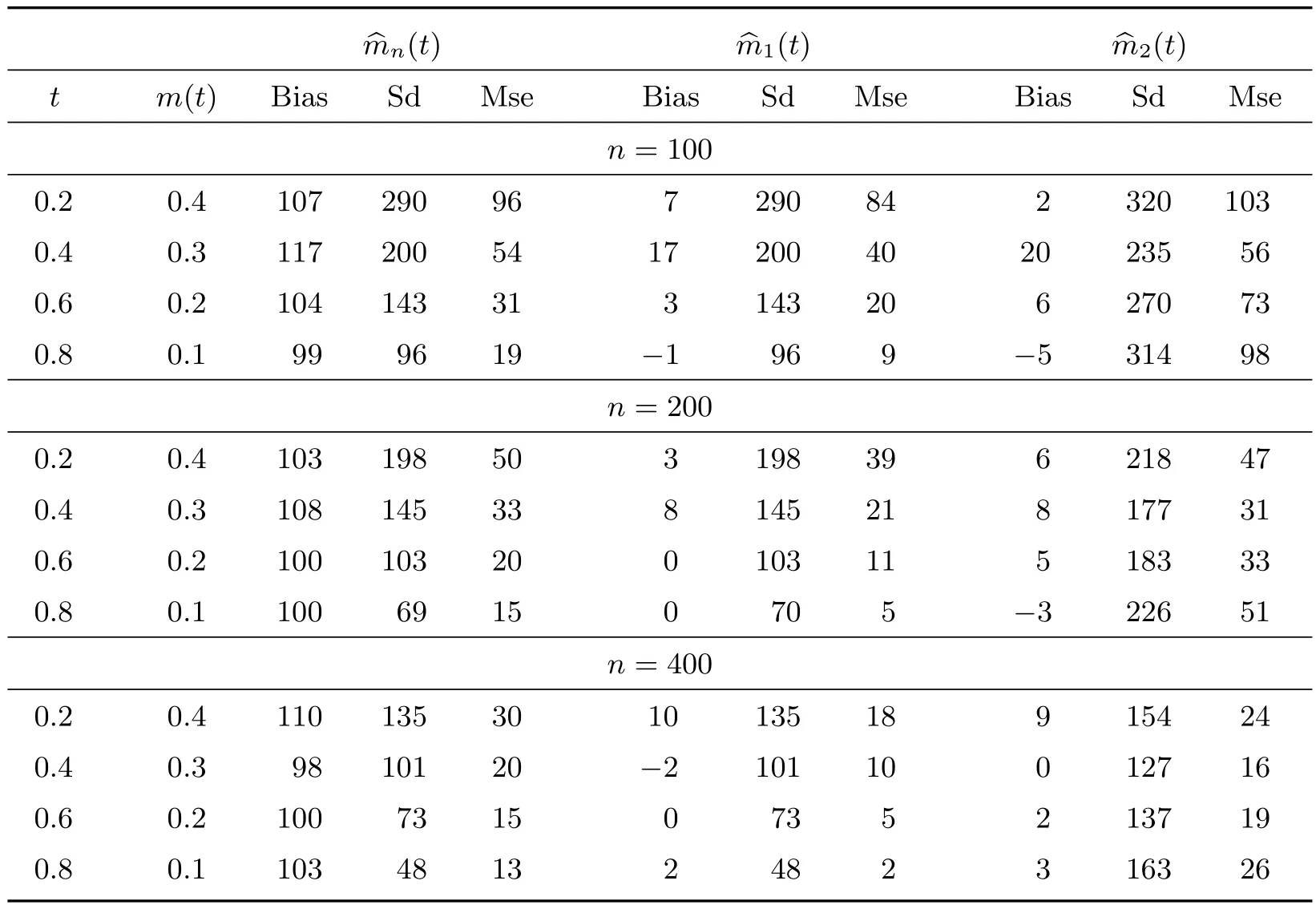
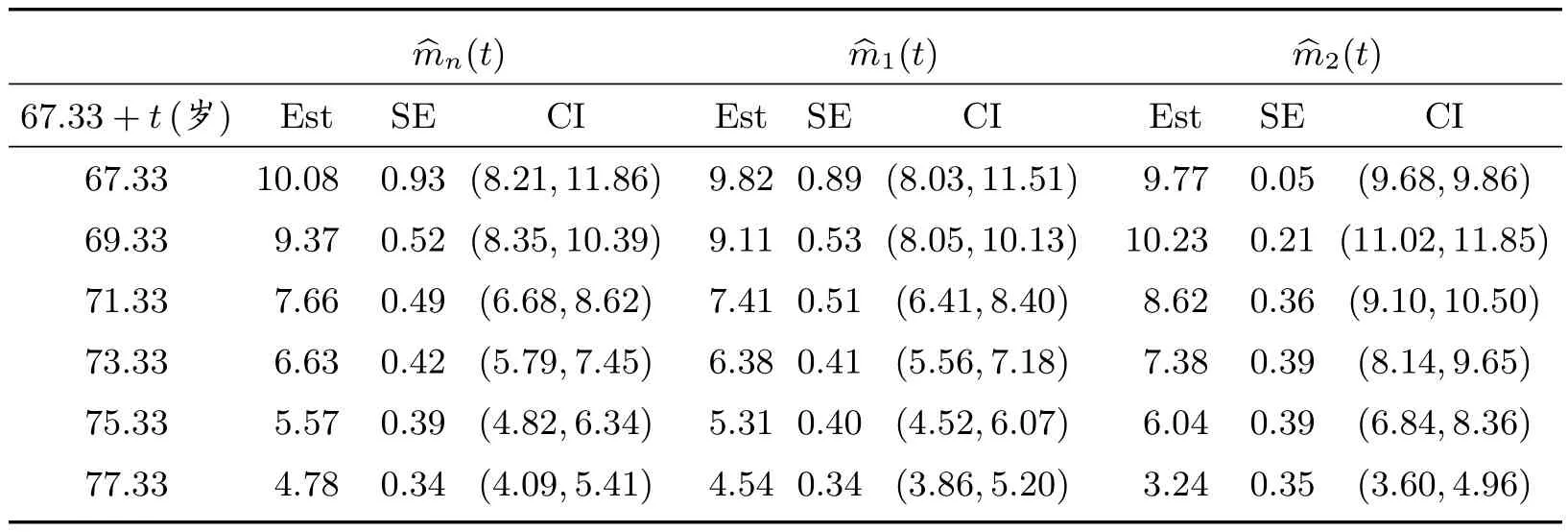
2.2 估计方法II

结合(2)式和(3)式可知，随机变量T0在时刻t的均值剩余寿命又可表示为

这里SA(t)表示随机变量A的生存函数，故易得其经验估计为

在长度偏差抽样机制下，A和V享有相同的概率分布；直观上讲，结合A与V的信息能够提升SA的估计精度。由于

故可得SA(t)的复合经验估计如下

从而，根据(6)式可得m(t)的另一矩类估计

其中0≤t

3 渐近性质

假设下列条件成立：

(C1)L是一非负常数，且满足0

(C2)S在[0,L]上绝对连续；

(C3) 0<µ=ET0<∞, Var(T0)<∞。记根据中心极限定理，可得如下结论。

引理1 若条件(C1)∼(C3)及(7)式成立，那么对任意的t ∈[0,L]，当n →∞时，有：

4 数值模拟

为了评价上述两个估计量的优劣，我们考虑两种方案进行模拟试验。在模拟过程中，样本容量n分别取100、200 和400 三种情况，且每次模拟试验重复的次数均为1 000。

方案I 感兴趣总体T0∼U(0,1)，左截断变量A0∼U(0,100)。重复产生(A0,T0)的随机数，直到有n组满足约束条件A0≤T0的数据为止。用︿mn(t)、︿m1(t)及︿m2(t)分别估计T0在t等于0.2、0.4、0.6 和0.8 时的均值剩余寿命。易知，在这四个点处，T0的生存概率分别为0.8、0.6、0.4 和0.2，且均值剩余寿命的真值分别为0.4、0.3、0.2 和0.1。模拟结果总结在表1 中，其中Bias=经验偏差×104，Sd=经验标准差×104，Mse=经验均方误差×105。

表1 方案I 中模拟结果比较

方案II 感兴趣总体T0服从威布尔分布，对应的生存函数为S(t)=exp(-t2/4)，且左截断变量A0∼U(0,100)。类似于方案I，重复产生n组满足约束条件A0≤T0的随机数据对(A0,T0)。用︿mn(t)、︿m1(t)及︿m2(t)分别估计T0在t等于0.94、1.43、1.91 和2.54时的均值剩余寿命。在这四个点处，T0的生存概率也分别为0.8、0.6、0.4 和0.2。均值剩余寿命m(t)在上述点处的真值分别为1.12、0.92、0.78 和0.64。模拟的数值结果总结在表2 中，其中Bias、Sd、Mse 的含义与表1 中的相同。

表2 方案II 中模拟结果比较

从表1 和表2 中的数值结果可以看出，三种方法所产生的经验偏差都比较小。除此之外，还可以得到如下结论；

1) 在两种方案中，由︿mn(t)模拟产生的经验偏差相对较大，而另外两种方法产生的经验偏差都很小；

2) 从经验标准差的角度来看，三种方法中︿m2(t)产生的经验标准差相对较大，而︿mn(t)和︿m1(t)产生的经验标准差非常接近。三种方法所对应的经验标准差都随样本容量的增大而越来越小；

3) 虽然︿m1(t)与︿mn(t)产生的经验标准差大小很接近，但是从经验均方误差的角度来看，︿m1(t)所产生的经验均方误差要比︿mn(t)的小得多，这在方案II 中尤其明显。当然，随着样本容量的逐渐增大，它们对应的经验均方误差也是逐渐减小。

综上可以看出，当样本容量n和时间点t给定时，︿mn(t)、︿m1(t)及︿m2(t)三种方法中︿m1(t)在经验偏差、经验标准差及经验均方误差三个方面中相对表现最好。

5 实际数据

Channing House 数据集是一个左截断右删失数据集，经过简单处理后可以得到一个长度偏差数据子集。因此，近年来经常作为一个长度偏差右删失数据实例进行研究[10,15]。该数据收集了在1964 年1 月至1975 年7 月期间入住美国Channing House 退休中心的462 名老人的生存数据，包括他们的性别、在该中心登记时的年龄、自登记时起到死亡或直至右删失事件发生时的持续时间。根据记录的结果可知，在这462 人中，共有男性97 名和女性365 名，其中有46 名男性和130 名女性于这段随访时间内死亡。基于删失的随机性和本文研究的长度偏差完全数据，下面我们将以这46 名男性和130 名女性生存数据为例，用以说明文中涉及的三种估计量的应用。

为了从这46 名男性和131 名女性生存数据中获取一个长度偏差完全数据，借助于文献[16]中提出的检验方法，我们发现死亡时年龄小于79.5 岁的103 人组成的数据集可以看作一个长度偏差完全数据子集，其中该子集中登记时年龄最小的是67.33 岁，这时记A从67.33 岁起至登记时的持续时间，V为从登记时起直至死亡时的持续时间。我们感兴趣的是这个子集中的成员随着时间的推移均值剩余寿命的变化情况。

表3 总结的是Channing House 长度偏差完全数据子集中退休人员在指定年龄的均值剩余寿命的估计值，其中Est 表示均值剩余寿命的点估计，SE 表示由简单Bootstrap 方法[17]得到的经验标准差，而CI 表示Bootstrap 置信区间，这里重复抽样的次数为R=1 000。由表3 中的结果可知，随着年龄的增加，子集中退休人员的均值剩余寿命是递减的。这也体现出了文中涉及的估计方法的合理性。