带单个变点AR(1)模型的统计推断
2024-01-03杨兰军吴刘仓
杨 磊, 杨兰军,, 吴刘仓
(1.昆明理工大学理学院,昆明 650500; 2.昆明理工大学应用统计学研究中心,昆明 650500)
0 引言
为方便讨论,本文常用记号规定如下:对于方阵A,tr(A)、AT、(A)i和rank(A)分别表示A的迹、A的转置、A的第i个主对角元素和A的秩;A-代表A的广义逆,即满足AA-1A=A;In表示n阶单位阵,1n表示元素都是1 的n维列向量,en(i)为第i个元素为1 其他元素为0 的n维列向量;a= arga∈Λ{F}表示a取集合Λ内满足属性F的值;Eθ0(·)和Dθ0(·)分别表示在模型参数取θ0条件下求期望与方差;o(1)和O(1)分别表示无穷小量和一致有界量;oP(1)和OP(1)分别表示依概率收敛到0 和依概率一致有界;P-→和d-→分别表示依概率收敛和依分布收敛。
时间序列模型一直都是统计学家研究的焦点和重点,但由于问题的复杂性,简单的时间序列模型往往不足以解决现实问题。当模型结构发生变化时,变点时间序列往往成为关注点之一。变点问题的处理方法在不断发展,在经典方法中,Hinkley[1]通过累积和(Cumulative Sum,CUSUM)方法研究了正态分布的均值结构变点问题;Brown 等[2]提出了累计平方和方法研究时间序列的方差变点问题;Incl´an 和Tiao[3]在Brown 等的基础上提出了迭代累积平方和方法用于检测独立随机序列的变点问题;Horv´ath[4]通过极限理论研究了自回归模型中变点的极大似然估计问题;Bai[5]基于最小二乘方法研究了线性过程的均值变点问题,得到了变点估计量的渐近分布;Galeano 和Pe˜na[6]通过CUSUM 方法研究了向量ARMA 模型在小样本下的方差变点检测问题;Liu 等[7]通过经验似然比方法研究了线性回归模型中的结构变点问题;Xia 等[8]通过加权残差的累计和方法以及移动和方法对广义线性模型进行了变点检测,考虑了检验统计量的渐近分布问题;Berkes 等[9]通过似然比检验研究了门限AR(1)模型的结构变点问题;Pang 等[10]研究了平稳和近似平稳情形下带有变点的AR(1)模型的渐近理论;Xia 和Qiu[11]提出了一种跳跃信息准则用于估计带有未知跳跃点的非连续曲线;谭智平和缪柏其[12]通过Kolmogorow 型统计量对连续随机变量的变点位置进行了检测;李订芳等[13]通过基于小波包的探测算法研究了时间序列变点问题;赵文芝和夏志明[14]基于加权残差的CUSUM 方法研究了线性模型渐变变点的检验问题。基于贝叶斯思想来研究时间序列变点问题的方法也得到了发展,McCulloch 和Tsay[15]利用Gibbs 抽样理论研究了均值和方差变点的自回归模型的统计推断问题;Chen 等[16]在贝叶斯框架下提出一种对双线性时序模型的变点检测算法;Slama 和Saggou[17]通过贝叶斯显著性检验研究了自回归模型的方差突变问题;熊立华等[18]通过贝叶斯方法,结合MCMC 抽样理论对水文时间序列的均值突变进行了研究。
目前大量的文献主要集中在对时间序列均值或方差变点问题的研究,对于回归函数参数变点问题的研究则相对较少,其中Chong[19]的研究特别值得关注。该文献就带有单个变点的AR(1)模型,基于最小二乘估计讨论了自相关系数估计量的相合性和极限分布。不同的背景和不同的研究方法可能得到不同的研究结果。本文主要考虑带单个变点AR(1)模型基于极大似然估计(Maximum Likelihood Estimate, MLE)或拟似然估计(Quasi-Maximum Likelihood Estimate, QMLE)的统计特征,主要包括三个方面:
1) 讨论了模型参数的MLE(或QMLE)及估计的存在性问题;
2) 讨论了自相关系数的MLE(或QMLE)的大样本特征;
3) 讨论了存在单个变点的自相关系数简单假设检验问题。
本文安排如下:第1 节讨论带单个变点AR(1)模型参数MLE(或QMLE)的表达形式及其存在性问题,给出了自相关系数MLE(或QMLE)的一致性和渐近正态分布结果,对关于变点前后的自相关系数ρ1、ρ2的假设H0:ρ2-ρ1=λ0的检验问题进行了讨论;第2 节通过数值模拟论证了自相关系数的一致收敛性质,通过上证综合指数日成交量数据,论证了模型是否存在单变点情况的假设(H0:ρ2-ρ1= 0)检验及自相关系数变化增量假设(H0:ρ2-ρ1=λ0)检验的有效性与合理性;第3 节是本文的总结部分。
1 主要内容
1.1 模型参数的极大似然(或拟似然)估计
本文考虑带有单个变点的一阶自回归(First-order Autoregressive, 简记AR(1))模型
其中E(X1) =µ/(1-ρ1), D(X1) =σ2/(1-ρ21),X1,ε1,···,εn-1为独立随机变量且存在常数γ>0,使得

从而,样本的对数似然(或拟似然)函数为

由于ρ1∈(-1,1)时,总有rank[B1(ρ1)]=n-q ≥1 且B1(ρ1)≥0,因而有P(XTB1(ρ1)·X>0)=1,即当ˆρ1存在且ˆρ1∈(-1,1)时,参数ρ2的估计为~ρ2(ˆρ1)且以概率1 存在。将~ρ2(ρ1)代入~L(ρ1,ρ2),得到关于参数ρ1的中心化对数似然(或拟似然)函数为
由(3)式、(5)式和(6)式知,模型参数µ∗、σ2、ρ2的极大似然(或拟似然)估计都与自相关系数ρ1密切相关,ρ1的估计成为得到模型参数极大似然(或拟似然)估计的关键且该参数的估计可以通过极大化L(ρ1)得到。由于L(ρ1)比较复杂,关于ρ1的显式解不易于获取,因此自相关系数ρ1极大似然(或拟似然)估计的存在性和一致性等性质的探讨具有重要意义。
由于

引理1 当q ≥1,n-q ≥1 且n ≥3 时,我们有:
(i) 0 (ii) 0 证明 假定q ≥2,n-q ≥1,由于 类似地,记 则P(-∞ 因而,当n ≥3 时,有 类似地,可证当q ≥1,n-q ≥1 且n ≥3 时,以下结论成立。 引理2 当q ≥1,n-q ≥1 且n ≥3 时,我们有: (i)f(ρ1)关于ρ1在(-1,1)连续; (ii) limρ1→1-f(ρ1)=∞, limρ1→-1+f(ρ1)=-∞几乎处处成立。 证明 假定q ≥2,n-q ≥1,由于 以概率1 成立。 由引理1 及(9)式,可得f(ρ1),ρ1∈(-1,1)连续,且limρ1→1-f(ρ1)=∞, limρ1→-1+f(ρ1)=-∞几乎处处成立。 类似地,可证当q ≥1,n-q ≥1 且n ≥3 时,结论成立。 定理1 在模型(1)中,当q ≥1,n-q ≥1 且n ≥3 时,参数ρ1的极大似然(或拟似然)估计ˆρ1以概率1 存在,且参数ρ1的极大似然(或拟似然)估计ˆρ1为f(ρ1) = 0,ρ1∈(-1,1)的零点。 类似地,可证当q ≥1,n-q ≥1 且n ≥3 时,结论成立。 在模型(1)中,对于模型参数µ∗、σ2、ρ1和ρ2的极大似然(或拟似然)估计,有以下结论成立。 定理2 对于模型(1),参数µ∗、σ2、ρ1和ρ2的极大似然(或拟似然)估计以概率1 存在的充分必要条件为q ≥1,n-q ≥1 且n ≥3,且模型参数的极大似然(或拟似然)估计ˆµ∗、ˆσ2、ˆρ1和ˆρ2有如下表达形式 证明 由定理1 可知,若ρ1的极大似然(或拟似然)估计ˆρ1存在且为f(ρ1) = 0,ρ1∈(-1,1)的零点,则有引理1 和引理2 成立。又由引理1 可知,当q ≥2,n-q ≥1 时,有 故若引理1 成立,则有q ≥2,n-q ≥1 且n ≥3 成立。结合定理1,即有ρ1的极大似然(或拟似然)估计ˆρ1存在的充分必要条件为q ≥2,n-q ≥1 且n ≥3。由于在此条件下,有P[~σ2(ρ1,~ρ2(ρ1))>0]=1,因此参数ρ1的极大似然(或拟似然)估计ˆρ1以概率1 存在时,模型参数µ∗、σ2和ρ2的估计也以条件概率1 存在。 综上,即有模型参数(µ∗,σ2,ρ1,ρ2)极大似然(或拟似然)估计以概率1 存在的充分必要条件为q ≥2,n-q ≥1 且n ≥3。 在模型参数的估计中,(5)式表明ˆρ2与参数ρ2的真实值ρ20有关。当|ρ20|≥1 时,并不能确保序列平稳,同时即使|ρ20|< 1,也不一定有|ˆρ2|< 1。因此,当|ρ20|<1 时,ˆρ2的一致收敛特征特别值得关注。 一致性研究是变点模型参数估计的一个重要部分。在|ρ2|< 1 和|ρ1|< 1 的条件下,下面讨论参数ρ1、ρ2极大似然(或拟似然)估计的一致性问题。为方便讨论,记p=n-q,模型参数θ的真实值θ0=(µ∗0,σ20,ρ10,ρ20),以及函数 则关于参数ρ1、ρ2极大似然(或拟似然)估计的一致性有如下重要结论。 上面论述表明(13)式成立。类似地,可以证明当q=1 且p →∞时,结论成立。 综上所述,结论成立[20]。 对于带单个变点的时间序列模型,单个自相关系数估计的大样本性质值得关注,但是是否存在变点更值得关注。在自相关系数估计一致性条件下,下面重点考虑参数λ=ρ2-ρ1极大似然(或拟似然)估计的渐近分布。 假设模型参数真值ρ10∈(-1,1),ρ20∈(-1,1),则有以下的定理5。 证明 假定q ≥2,n-q ≥1,作参数变换λ=ρ2-ρ1,则关于参数ρ1和λ的中心化对数似然(或拟似然)函数(ρ1,λ),ρ1∈(-1,1),λ ∈(-2,2)为 则由定理5,有 其中 类似地,可以证明当q=1 且p →∞时,结论成立。 在定理5 和定理6 中,它们的渐近分布都只和自相关系数真值有关。特别值得注意的是,定理6 的实际意义在于它可用于对模型单个变点的假设H0:ρ2-ρ1=λ0进行检验,其中λ0不一定为0。当λ0= 0 时,假设H0:ρ2-ρ1=λ0的检验等价于假设H0:ρ2=ρ1的检验,即检验是否存在变点。下面讨论更一般的简单假设检验H0:ρ2-ρ1=λ0。 本小节主要通过模拟数据对第1 节中所提的方法及相关结论进行检验。假定数据生成模型为 下面模拟不同参数取值下模型自相关系数极大似然(或拟似然)估计ˆρ1、ˆρ2在q=o(p),p →∞时的收敛情况。模拟实验重复进行10 000 次,其中q= 80,25,6 对应的p=20,275,994,此时q/p逐步增大。记录自相关系数极大似然(或拟似然)估计值的均方误差,得到结果见表1。 表1 随机模拟结果 从表1 可以看出,随着p的增大,自相关系数极大似然(或拟似然)估计ˆρ1、ˆρ2的均方误差都有趋于零的特征,表明自相关系数极大似然(或拟似然)估计值收敛到真值,自相关系数极大似然(或拟似然)估计分别是对应参数真值的一致估计。 下面将带有变点的模型(1)应用于实证研究,主要分析上证综合指数日成交量从1998 年1 月5 日至2003 年1 月29 日的1 221 个数据的变点检验问题,其时间序列图见图1。 图1 上证综合指数日成交量时序图 对于上证综合指数日成交量序列的样本自相关和偏自相关系数,如图2 和图3 所示,其中样本的自相关系数呈指数递减趋势,表现为拖尾性;偏自相关系数表现为1 阶截尾性质,初步选择AR(1)模型刻画该序列。 图2 上证综合指数日成交量序列的自相关系数 图3 上证综合指数日成交量序列的偏自相关系数 对该时间序列,需要找出其变点位置。通过对不同q值做假设检验H0:ρ2-ρ1=0 得到变点位置,与刘琴[21]通过极大似然比方法得到的变点位置一致。本文基于此变点位置主要研究H0:ρ2-ρ1=λ0的检验问题。由于模型参数的极大似然(或拟似然)估计值如表2 所示,则可构建假设H0:ρ2-ρ1=-0.270 4 进行检验,以确定该序列在此位置存在变点且自相关系数增量为-0.270 4。在原假设成立条件下,由定理6,有,从而可得到ˆλ在1-α=0.95 的显著性水平下的临界点u1=-0.318 3,u2=-0.222 5,故在95%的显著性水平下可考虑接受原假设,即可以认为该序列在t=80 时刻存在持久性变点且ρ20=ρ10-0.270 4。该实证研究表明本文所提出的方法是方便且有效的。 表2 极大似然(或拟似然)的估计结果 本文主要研究了带单个变点AR(1)模型的统计推断问题。基于极大似然(或拟似然)方法,本文给出了模型参数极大似然(或拟似然)估计的一种表达形式,得到了一般条件下自相关系数极大似然(或拟似然)估计一致收敛到参数真值的特征,并给出了其渐近分布,同时通过该分布,解决了对变点是否存在的简单假设的检验问题。数值模拟验证了自相关系数极大似然(或拟似然)估计一致性;实证分析的结果表明了变点存在问题的检验方法的有效性,该检验方法具有一定的实际意义。




1.2 自相关系数估计的一致性
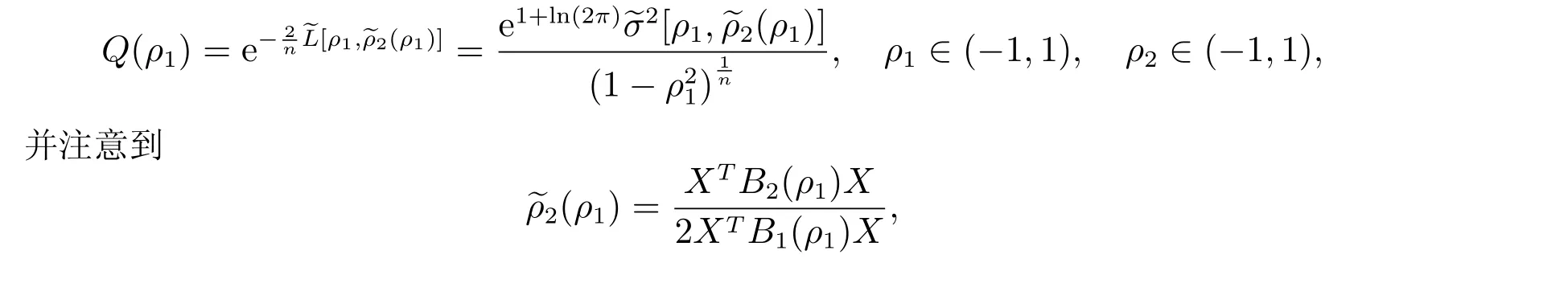

1.3 估计的渐近分布



2 模拟研究和实证分析
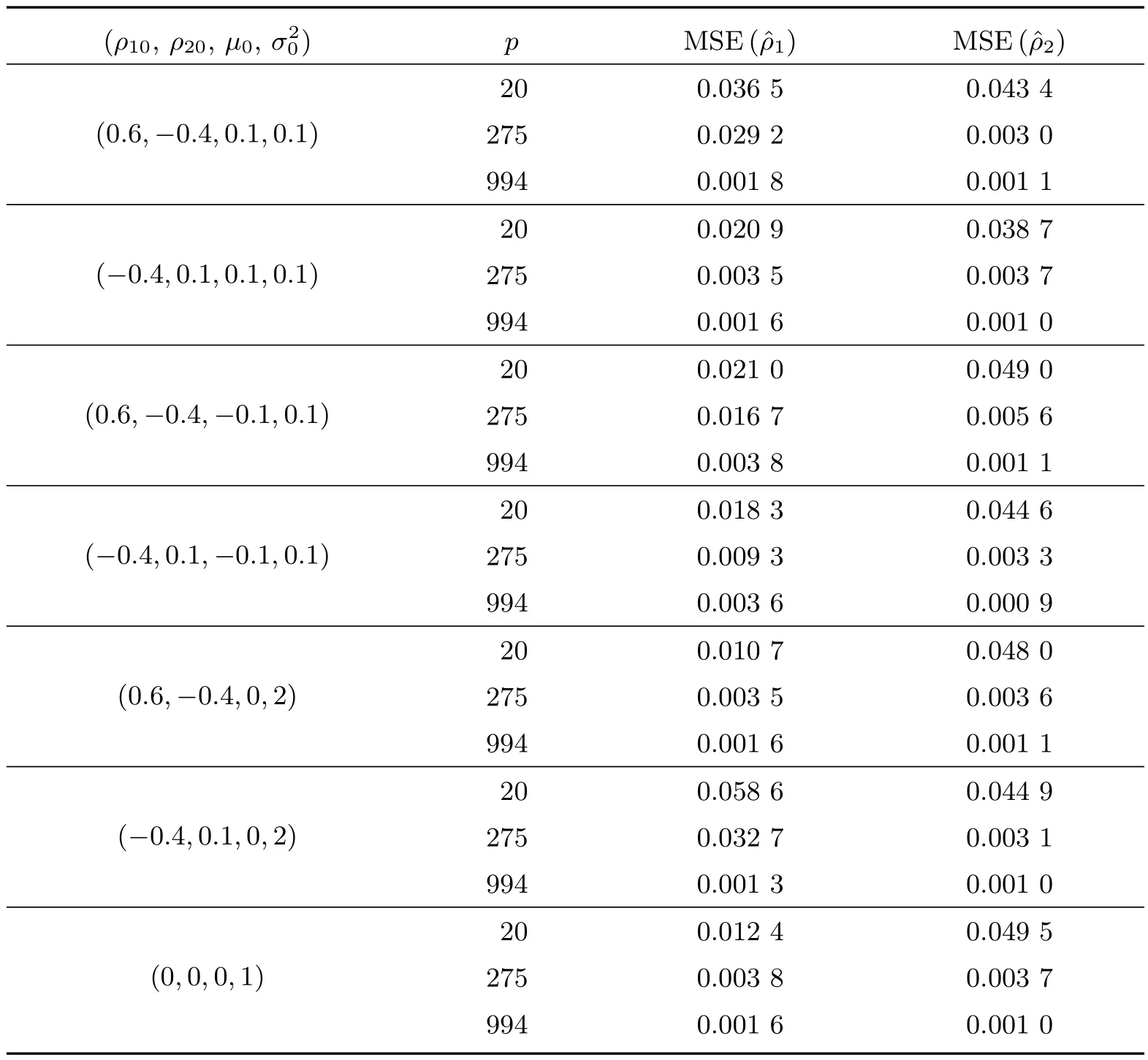
2.1 自相关系数估计一致性的数值模拟
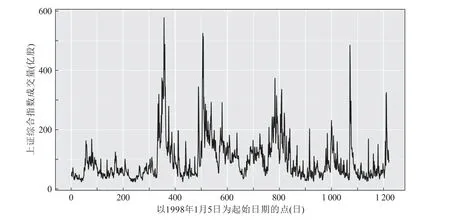
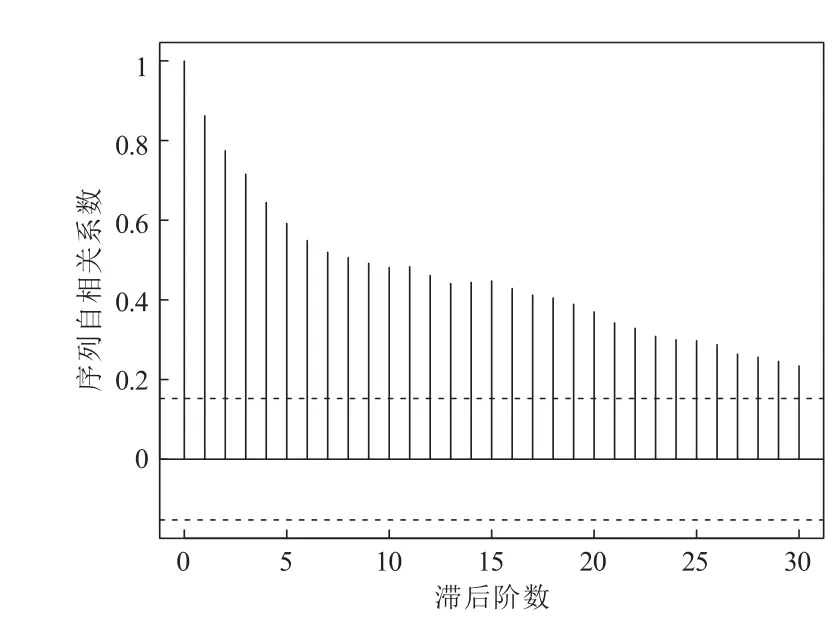
2.2 实证分析


3 总结
