带有CVaR 罚的分布鲁棒指数跟踪模型:易求解的转化
2024-01-03王茹钰胡耀忠
王茹钰, 胡耀忠, 张 超,
(1.北京交通大学数学与统计学院,北京 100044;2.加拿大阿尔伯塔大学数学与统计科学系,埃德蒙顿 T6G 2G1)
0 引言
指数跟踪通过最小化衡量所构建投资组合与基准指数的接近程度的跟踪误差,从而构建由市场中的资产组成的投资组合。指数跟踪在近年来受到了广泛关注。Xu 等人[1]在最小化二次跟踪误差的基础上,设置投资组合中资产数量的上限,并提出了一种用于解决该模型的非单调投影梯度方法。Zhang 等人[2]在目标函数中引入了ℓ2和ℓp(0 近年来,分布鲁棒优化(Distributionally Robust Optimization, DRO)在多个领域中得到了广泛的应用,包括指数跟踪和数据挖掘[7–12]。Kang 等人[7]通过整合由ϕ-散度定义的分布不确定信息,提出了一个DRO 指数跟踪模型。Liu 等人[13]给出了分布鲁棒均值-CVaR 投资组合选择问题的显式最优解。由于该问题的目标函数是一个简单的线性函数,因此通过鲁棒优化中的最大化问题可以得到一个显式解。由于一般指数跟踪问题目标函数具有非线性性质,难以获得指数跟踪问题的显式解。Xu 等人[14]分析了最小最大DRO 问题的强Lagrange 对偶条件,并提出了一种解决DRO 对偶问题的离散化方案。Chen 等人[15]将该离散化方案推广到解决两阶段分布鲁棒线性互补问题。Jiang 和Chen[16]提出了一个带有离散化的近似问题,以解决具有随机互补约束的分布鲁棒纯特征需求模型。对于输入数据及其相应分布存在不确定性的问题,DRO 相比于确定性问题和随机优化问题更加有优势。在实践中,较难获取随机向量的真实概率分布,这促使将DRO 的思想引入到指数跟踪模型中。 在本文中,提出了一个在目标函数中同时包含ℓ2范数惩罚和CVaR 惩罚的分布鲁棒指数跟踪模型(简称DRCVaR 指数跟踪模型)。分布的不确定性通过随机向量的一阶和二阶矩的置信区域来描述。将分布鲁棒的思想与指数跟踪误差相结合,能够较好地反映信息不确定性,同时使用ℓ2范数来避免过度拟合,并在原始的指数跟踪模型中使用CVaR 惩罚进行风险控制。然而,这些惩罚项也使其在可行性和计算效率方面充满挑战。DRCVaR 模型是一个“min-max-min”优化模型,根据文献[17]中的最小最大定理,将DRCVaR 等价转化为一个“min-max”优化问题。由于内部的最大化问题满足上述分布模糊集中的Slater 条件,通过Lagrange 对偶将内部的最大化问题等价地转化为半定规划(Semi-Definite Programming, SDP)问题,以此等价转化DRCVaR 为一个SDP 模型。同时,证明了该SDP 模型是凸的且最优解集合是非空的。若原分布是连续的,则该SDP 模型的目标函数中将包含无限多个非光滑凸函数的最大化。该问题通过一种离散化方案近似为包含众多但有限个非光滑凸函数最大化的问题,并提供了离散化方案的收敛性证明。 众所周知,光滑化方法能够有效解决非光滑优化问题[18–25]。Nesterov[18]通过使用具有Lipschitz 连续梯度的函数来近似非光滑的目标函数,并通过高效的梯度方法来最小化该光滑函数。Zhang 和Chen[19]提出了一种解决闭凸集上最小化问题的SPG 方法。Zhang 和Chen[20]提出了一种用于最小化线性约束非Lipschitz 非凸问题的光滑积极集方法。Bian 和Chen[21]开发了一种光滑的近端梯度算法,用于求解一类由非光滑凸函数和基数函数之和定义目标函数的约束优化问题。Chen 等人[26]提出了一种光滑的样本均值近似方法,用于最小化期望残差函数。受上述方法的启发,本文采用光滑化函数近似由对偶和CVaR 惩罚引起的所有非光滑凸函数。与上述非光滑凸函数相比,众多非光滑凸函数的最大化涉及双层非光滑函数,该函数的光滑化具有一定挑战。受现有指数跟踪模型的特性和数值可行性的启发,本文将DRCVaR 模型等价地转化,并使用SPG 方法高效地解决DRCVaR 模型。 第1 节,简要回顾重要的指数跟踪模型,基于已有模型的优点与不足提出了DRCVaR模型,并将该模型在分布模糊集中的内部最大化问题转化为SDP 问题。第2 节,等价转化DRCVaR 模型为一个易求解的模型,同时证明了转化后的问题是凸的且最优解集合是非空的。由于等价转化后问题的目标中包含无限多个非光滑凸函数的最大化,在第3 节中,通过一种离散化方案离散为包含众多但有限个非光滑凸函数最大化的问题,并给出了收敛性证明。第4 节,利用SPG 方法来求解包含众多但有限个非光滑凸函数最大化的问题,同时证明了任何聚点是离散化问题的全局最小值点。第5 节,通过与不同的模型及其对应算法进行比较,得出DRCVaR 模型和SPG 方法的优越性。第6 节为总结。 本文使用Sd+表示对称正半定矩阵锥,//x//表示向量x的欧几里得范数。对于数r ∈R,用[r]+= max{r,0}表示正部函数。给定两个方阵M和N,M ≼N表示N-M是正半定的。矩阵内积〈M,N〉表示两个具有相同维度的矩阵M和N之间的内积,即〈M,N〉 = ∑i,j Mi,jNi,j。闭球B(x,δ) :={y ∈Rd://x-y//≤δ}表示以x ∈Rd为中心,半径为r的闭球。 本节介绍用于指数跟踪投资组合选择问题的DRCVaR 模型,并分析其性质。下面简要回顾一些重要的指数跟踪模型。 其中第一项是数据保真度项,凸函数ψ描述跟踪投资组合的收益率与指数收益率之间的偏差,ψ(a) =|a|或ψ(a) =a2。第二项中的函数R是惩罚项,可以帮助控制风险,反映投资组合的稀疏性,增强样本外表现等。参数τ平衡数据保真度项和惩罚项之间的权衡。可行集X是一个凸集,其中包括关于投资组合的先验知识,例如 下面概述一些可以用通用模型(1)表示的指数跟踪模型。 在文献[27]中,Lasso 稀疏指数跟踪问题可以表述为 其中τ1是给定的正则化参数,ℓ1范数惩罚旨在增强投资组合的稀疏性。由于该模型没有非负约束,因此可能出现负权重从而导致卖空。(Lasso 稀疏)模型使用优化软件“CPLEX”求解。 在引入CVaR 风险度量的情况下,Wang 等人在文献[6]中提出了具有CVaR 风险约束的混合0-1 LP 指数跟踪模型 其中K是选择跟踪指数的股票数量,Zi=1 表示在跟踪投资组合中包含第i只股票,Zi=0 表示不包含,li和ui是资产i的投资比例的下限和上限,0 Xu 在文献[1]中提出了控制投资组合中资产数量上限且最小化二次跟踪误差的指数跟踪模型 其中//x//0表示x的非零分量的个数,K是给定的正整数,u ∈[1/K,1]是每个指数成分的权重的上限。在文献[1]中,Xu 等人提出了一种非单调投影梯度法来解决该问题。 Zhang 等人在文献[2]中构建了以下稳健且稀疏的非凸指数跟踪模型 其中0 投资组合的样本外表现比样本内表现更加重要,当指数的真实回报率和投资组合的真实回报率尚不明朗时,确定性指数跟踪模型得到的投资组合可能产生样本内表现优异,但样本外表现欠佳的情况。为了解决该问题,替代使用全部历史数据,将ξB= (ξB,1,ξB,2,···,ξB,d)∈Rd视为随机回报向量,ξa ∈R 视为相应的随机市场指数回报。定义随机向量ξ:=(ξ⊤B,ξa)⊤∈Rd+1,假设ξ的概率分布为P。将确定性问题(1)推广为以下具有CVaR 惩罚的随机指数跟踪投资组合模型 其中x=(x1,x2,···,xd)⊤是决策向量,每个分量xi表示投资于资产i(1≤i ≤d)的资金占总金额的比例,并且正则化参数τ1,τ2≥0。惩罚项CVaR 定义为 其中ℓ(x,ξB)是关于x ∈X的凸损失函数,本文定义ℓ(x,ξB)与文献[4]相同 模型(SCVaR-P)可以使用随机次梯度(S-Subgrad)方法[32–33]求解。 在实际应用中,假设随机变量ξ遵循真实概率分布P是合理的,但P并不是ξ的准确分布。分布P包含在使用历史数据等部分信息构建的分布模糊集P中,这一观察促使本文在指数跟踪模型中采用分布鲁棒优化的思想。因此,本文提出了如下的DRCVaR 模型 由于惩罚项CVaR 的定义(4)中包含期望形式,可知模型(5)中maxP ∈P对数据保真项EP[ψ(ξa-ξ⊤Bx)]以及罚项ϕB(x)同样作用。令ˆµ和ˆΣ分别表示历史数据(ˆξ1,ˆξ2,···,ˆξN)的均值向量和协方差矩阵的参考值,假设ˆΣ是对称正定矩阵。模型(5)的分布模糊集P通过前两阶矩约束构建[8,14] 其中κ1>0,κ2>0,M是可测空间(Ξ,B)中所有概率测度的凸集,其中Ξ ⊆Rd+1是已知包含P的支撑集的凸紧集,B 是Ξ上的Borelσ-代数。 引理1[34]给定一个如下的分块对称矩阵 其中A是对称矩阵。若det(A)̸=0,则矩阵ˆS=C-B⊤A-1B被称为ˆM中A的Schur 补。若A ≻0,则ˆM ≽0,当且仅当ˆS ≽0。 根据引理1,分布模糊集(6)中的第一个约束可以等价地改写为 第2 节考虑原模型(5)的等价转化形式,在其转化过程中,首先根据最小最大定理将模型(5)中的minx∈∆dmaxP ∈Pminα∈R等价转化为minx∈∆dminα∈RmaxP ∈P,然后固定外层最小化问题的变量x ∈∆d和α ∈R,考虑内部最大化问题的对偶形式。为简化第2 节中的等价转化证明过程,此处先考虑在分布模糊集(6)上的如下最大化问题 则最大化问题(7)等价于下面的半无限规划问题 其中r ∈R,q ∈Rd+1和Λ ∈R(d+1)×(d+1)是对偶乘子。此外,对偶问题(10)的最优解集是非空的。 命题1 通过Lagrange 对偶将内部最大化问题(7)转化为一个半无限规划,并证明了在分布模糊集(6)中内部最大化问题(7)的Slater 条件被满足。在DRO 中矩问题满足Slater 类型条件时原问题和对偶问题等价,由此可得内部最大化问题(7)与其对偶问题等价。 命题1 的证明与文献[8]中引理1 的证明相似,若直接套用文献[8]引理1 中对偶问题的结果,则(8)中与随机向量ξ无关的项τ1//x//2与τ2α会出现在对偶问题(10)的无限约束中,但这并不影响后面最终等价问题(14)的形式。为了使(10)的无限约束只存在与随机向量ξ相关的项,下面仿照文献[8]引理1 给出命题1 的证明。 根据文献[14]中的例2.3,问题(6)的矩约束满足Slater 类型条件(13)。因此,问题(7)与问题(10)之间的等价性成立。由于支撑集Ξ是紧的且问题(7)的目标函数内层的ˆK在Ξ上连续,得到问题(7)的最优值是有限的。根据文献[35]中的命题3.4,若原始问题和对偶问题的相同最优值是有限的,则对偶问题的最优解集是非空的。因此,推断出对偶问题(10)的最优解集是非空。 定义ν=(x,α,q,Λ)和V=∆d×R×Rd+1×Sd+1+。根据CVaR 的定义(4),问题(5)可改写为一个“min-max-min”优化问题。本节将该问题等价转化为一个非光滑SDP 问题 其中 而h1和h2,ξ在(9)式中定义。 引理2[14,36]若Ξ是一个紧集,则(Ξ,B)上的所有概率测度集合关于弱收敛拓扑是弱紧的。 定义1[14](i) 对于一个概率测度集合¯A ⊂M,若每个序列{PN} ⊂¯A都包含一个子序列{PN′}和一个概率测度P ∈¯A,使得PN′→P,则称¯A关于弱收敛拓扑是弱紧。 (ii) 在弱收敛拓扑下,若对任意序列{PN} ⊂¯A,其中PN →P是弱收敛的,且有P ∈¯A,则称¯A是闭的。 由于Ξ在分布模糊集(6)中是一个紧集,根据定义1 和概率测度在紧集上有界的性质,可以得到在(Ξ,B)上的所有概率测度的集合在弱收敛拓扑下是紧的。 引理3[17]若ˆA是紧的,ˆB是任意的空间,对于每个α,函数ρ(P,α)关于P是凹的,并且对于每个P,函数ρ(P,α)关于α是凸的。对于每个α,函数ρ(P,α)关于P是上半连续的,则 定理1(DRCVaR 转化为非光滑SDP) 对于DRCVaR 问题(5)以及非光滑SDP 问题(14),有min(5)=min(14),即x是(5)的最优解,当且仅当存在α ∈R,q ∈Rd+1和Λ∈Sd+1+,使得(x,α,q,Λ)是问题(14)的最优解。 证明 根据ˆK的定义(8),问题(5)等价于以下问题 由于分布模糊集(6)的支撑集Ξ是紧的,根据定义1,函数ˆK(x,α,P)相对于α是凸的(来自线性和正部函数的凸性),相对于P是凹的(事实上是线性的),以及P的紧性,可以使用引理3 交换(16)中的maxP ∈P和minα∈R得到等价转化 固定x和α,由命题1 得到问题(7)与对偶问题(10)之间的等价性。由于样本空间Ξ中有无限多个ξ的值,半无限规划问题(10)中存在无限多个约束h2,ξ(x,q,Λ)≤r,∀ξ ∈Ξ。上述无限约束可被改写为 则Lagrange 对偶问题(10)等价于 通过“min-min”算子联合执行得出DRCVaR 的一个等价转化问题(14)。 定理1 将DRCVaR 指数跟踪模型(5)等价转化为SDP 问题(14)。由∆d和P的有界性,以及模型(5)中的目标函数在这两个有界集中的连续性得到原问题(5)的解集是非空。同时,定理1 保证了SDP 问题(14)的最优解的存在性。 为便于实际中计算求解,本节针对SDP 问题(14)提出一种离散化方案,在较弱的条件下证明了离散化模型的解的存在性。同时,在较弱的假设下,提供了离散化模型的最优值和解与概率分布连续的模型的最优值和解之间的关系。 由凸函数的定义可证明hξ(ν)关于ν是凸函数。根据文献[37]的命题1.38,有限个凸函数的最大化函数也是凸的,即φN(ν)关于ν是凸的。此外,可行集V是一个凸集。因此,非光滑模型(18)是凸的。 若采样得到一组向量ξ1B,ξ2B,···,ξNB,由(19)式可知ϕNβ(x)关于α的最优解在有限的α处达到,即可将α的最小化限制在某个足够大的正数c的闭区间[-c,c]内[4,14]。令A 为由ϕNβ(x)最小值处的α值组成的紧集。由于∆d和Ξ[N]的紧性,存在x∗∈∆d和ξ∗∈Ξ[N]作为离散化问题(18)的最优解。因此,离散化问题(18)的解集是非空的。 定义离散化问题(18)和问题(14)的最优值分别为ˆϑN和ˆϑ。定理2 陈述了问题(18)与问题(14)的最优值收敛关系。 定理2 假设问题(7)的最优值是有限的,ξ1,ξ2,···,ξN是ξ的i.i.d.的样本,并且ξ在Ξ上服从连续的概率分布P,对于任何固定点ξ0∈Ξ和δ ∈(0,δ0),满足以下条件 其中C2、γ2和δ0是一些正的常数。当N足够大时,对于任何正数ε,存在正的常数ˆC(ε)和ˆβ(ε),满足以下不等式 证明 (i) 定义随机变量h(ν,ξ)-E[h(ν,ξ)]的矩生成函数为 由于Ξ是一个紧集,根据文献[14]的第3.1 节,对于每个ν ∈V, supξ∈Ξ h(ν,ξ)<∞,并且矩生成函数Mν(t)在零的某个邻域内存在有限值。 (ii) 根据函数h的连续性,存在一个非负可测函数κ:Ξ →R+和一个常数γ> 0,使得对任意的ξ ∈Ξ,有 (iii) 根据支撑集Ξ的有界性和文献[38]的第5 节,可得随机变量κ(ξ)的矩生成函数Mκ(t)在零的某个邻域内有限。 结合上述条件(i)∼(iii)、条件(20)和函数h(ν,·)在Ξ上的连续性,可得问题(18)与问题(14)的最优值的关系,即(21)式成立[14]。 注1 根据文献[39]的命题1,条件(20)实际上是较弱的,若随机向量ξ的密度函数被一个解析的正实值函数从下方界定,则条件(20)成立。条件(20)实际上是密度函数在其支撑边界接近零的条件。 注2 根据文献[14]中的例3 和定理4 可知,使用内点方法求解模型(5),要求随机变量ξ的支撑集Ξ是一个紧的椭球集合。然而,本文没有对支撑集Ξ的形式施加任何限制。 在文献[14]中,内部最大化问题中的目标函数被要求关于ν是可微的。在模型(18)中,hξ(ν)包含了由ℓ2范数和正部函数引起的不可微项。因此,文献[14]中提出的算法3.1 不能直接求解模型(18)。下节将构造一个光滑化函数并采用SPG 方法来求解模型(18)。 定义2[23]令g:V →R 为一个连续函数,称˜g:V×R+→R 为g的光滑化函数,若对于任意固定的µ>0,˜gµ(·) 在V中是连续可微的,并且 此外,{limz→ν,µ↓0∇ν˜gµ(z)}是非空且有界的。 定义3[40]若对于所有v,有: (i) 存在通常的单侧方向导数f′(w;v); (ii) 对于所有v,g′(w;v)=g◦(w;v),其中 则称函数g在w处是Clarke 正则的。 引理4[23]假设和是局部Lipschitz 函数Γ:RN →R 和π:V×Ξ[N]→RN的光滑化函数,且向量函数 若Γ在W(ν,Ξ[N])处是Clarke 正则的,π在(ν,ξ)处是Clarke 正则的,且 则对于任何ν ∈V,()都是Γ(W)的光滑化函数。 引理5[40]设ˆg在ν附近是Lipschitz 连续的。若是凸函数,则在ν处是Clarke 正则的。 对于一个向量函数 其分量为h(ν,ξi):V×Ξ →R, 1≤i ≤N,显然有 依据引理4 和引理5,命题3 为非光滑复合函数Φ(H)构造光滑化函数。 命题3 对于任意固定的ξ和光滑因子µ>0,在(15)式中定义的h(ν,ξ)和(18)式中定义的φN(ν)的光滑化函数分别为 由于h(ν,ξ)和Φ(ˆχ)的凸性,以及引理4 和引理5,可知(23)式中的˜φNµ(ν)是φN(ν)的光滑化函数。 基于上述讨论,则可给出如下的SPG 算法。 算法1 SPG 方法 给定α0,σ,ρ,ω ∈(0,1),µ0,η> 0,ϵ> 0,ν0∈V,以及正整数n0> 0。对于k ≥0,则: 则设置νk+1=yj+1,k,然后转到步骤3; 步骤3 选择µk+1≤ωµk。 步骤2 中的j ≥n0是由文献[19]提出的,用于判断算法是否进入步骤3 进而减小光滑因子µk。对于每个µk,至少执行n0次内部迭代。从计算角度来看,该修改有助于光滑化方法找到全局或更好的局部最优解。 对于任意固定的¯ν ∈V,将Clarke 次微分定义为 与光滑化函数相关的次微分定义为 从定义2 中可以明显看出,G˜φNµ(¯ν)是一个非空且有界的集合。 定义4 若存在U ∈G˜φNµ(ν∗),使得〈U,ν∗-z〉≤0,∀z ∈V,则称ν∗是问题(18)的一个与光滑化函数相关的稳定点。 定义5 若存在U ∈∂φN(v∗),使得〈U,ν∗-z〉≤0,∀z ∈V,则称ν∗是问题(18)的一个Clarke 稳定点。 假设投资者使用投资组合优化模型(18),对2008 年1 月至2023 年7 月的纳斯达克日度指数数据集中的120 只股票进行投资组合,该指数数据集包含3 921 个样本。本节所有实验均在3.70 GHZ Intel Core 10 CPU 和64 GB RAM 的Windows 10 系统上,使用Matlab R2021a 软件运行。 本文采用日度数据的滚动窗口方法[41]以在样本外环境中评估投资组合。设置窗口大小为3 500 个日度观测值,即在离散化问题(18)中N= 3 500。首先,使用前τ个收益观测值来计算最优权重向量。然后,假定该投资组合在接下来的21 天内持有。将这21 天的数据用作测试向量Bt+1∈R120来计算样本外表现,其中(Bt+1)i表示第i个资产的21 天内最后一天的收盘价与第一天的开盘价之比,at+1∈R 是观察到的对应的随机市场指数回报。在此期间,投资者基于投资组合获得的财富表示为在这21 天后,投资组合根据基于Bt+1转变为,其分量由计算,如文献[42]的第2 节所指出的。在下一步中,滚动数据窗口前进,舍弃最旧的观测值,将最新的21 个观测值包含到训练集中。使用新的训练集解决模型(18),得到解+1,然后将+重新平衡到新的权重向量+1,确定了投资组合持仓以及未来21 天的样本外回报。该过程重复进行,直到无法再滚动窗口,即t= 1,2,···,¯t=⎿(Ntol-τ)/21」。上述设置中Ntol=3 921,τ=3 500,则¯t=20。 使用投资组合的样本内跟踪误差(TEI)和样本外跟踪误差(TEO)衡量给定模型的性能,其定义如下 或者迭代次数超过3 000。设置κ1= 0.1 和κ2= 1,这些参数与模型(6)中的参数相同,与文献[11]的数值实验一致。 为了测试SPG 方法的效率,将其与次梯度(Subgrad)方法在前3 500 个训练样本中共同求解带有ψ(a) =a2的模型(18)。在Subgrad 方法中使用Armijo 步长规则,设置τ1=τ2= 10-2。SPG 方法和Subgrad 方法在训练集中的目标值(Obj)与CPU 时间之间的关系被绘制在图1 中,对应的样本内、外表现以及CPU 时间在表1 中。从图1 可以看出SPG 方法下降速度更快,并且在表1 中的样本内、外表现以及CPU 时间都优于Subgrad 方法。 表1 样本内、外表现以及CPU 时间 图1 目标函数值与CPU 时间的关系 下面将使用ℓ1范数的DRCVaR 模型(DRCVaR-ℓ1)和使用ℓ2范数的DRCVaR 模型(DRCVaR-ℓ2)与第1.1 节中的指数跟踪模型进行比较,包括(Lasso 稀疏)模型、(混合0-1 LP)模型、(TE-ℓ0)模型、(ℓ2-ℓ3/4)模型和(ℓ2-ℓ1/2)模型,上述模型求解方法见第1.1 节中的说明。同时比较了两个随机模型,即具有ℓ1范数的SCVaR- ˆP 模型(SCVaR- ˆP-ℓ1)和具有ℓ2范数的SCVaR- ˆP 模型(SCVaR- ˆP-ℓ2),ˆP指的是从历史数据中获得的经验分布。通过在网格 上变化τ1和τ2的取值,选择每个模型中对应最低TEO 的参数值作为τ1和τ2的最优参数值。表2 中记录了最低的TEO,以及相应的参数τ1、τ2、样本内和样本外性能。对于参数τ1和τ2,“—”表示在相应的模型中不需要对应的参数。在所有评估标准中,除了TO 之外,(DRCVaR-ℓ2)模型在其他方面表现优于(DRCVaR-ℓ1)模型。显然,当配备适当的参数并使用SPG 方法求解时,DRCVaR 模型在样本内和样本外性能都优于其他模型。将(DRCVaR-ℓ2)、(DRCVaR-ℓ1)与(SCVaR- ˆP-ℓ2)、(SCVaR- ˆP-ℓ1)的结果进行比较,发现DRO 可以提高模型的样本外性能。此外,相较于模型(SCVaR- ˆP-ℓ2)和(SCVaR- ˆP-ℓ1),模型(DRCVaR-ℓ2)和(DRCVaR-ℓ1)因为使用SPG 方法缩短了CPU 时间。 表2 根据最小的TEO 确定τ1 和τ2 的值以及参数对应的样本内、外表现 本文将分布鲁棒优化和条件风险值惩罚相结合,提出了一个新的指数跟踪模型,该模型的分布模糊集由前两阶矩来定义。本文将该分布鲁棒指数跟踪模型等价转化为非光滑凸优化问题,并为其中的连续随机向量提供了一个近似的离散化方案。在离散化之后,目标函数包含了众多但有限个非光滑凸函数的最大化,采用SPG 方法来求解该离散化问题。基于2008 年1 月到2023 年7 月的纳斯达克日度指数数据集进行数值比较,数值结果展示了本文提出的模型以及SPG 方法的有效性。1 DRCVaR 指数跟踪模型
1.1 使用精确历史数据的确定性模型

1.2 DRCVaR 模型
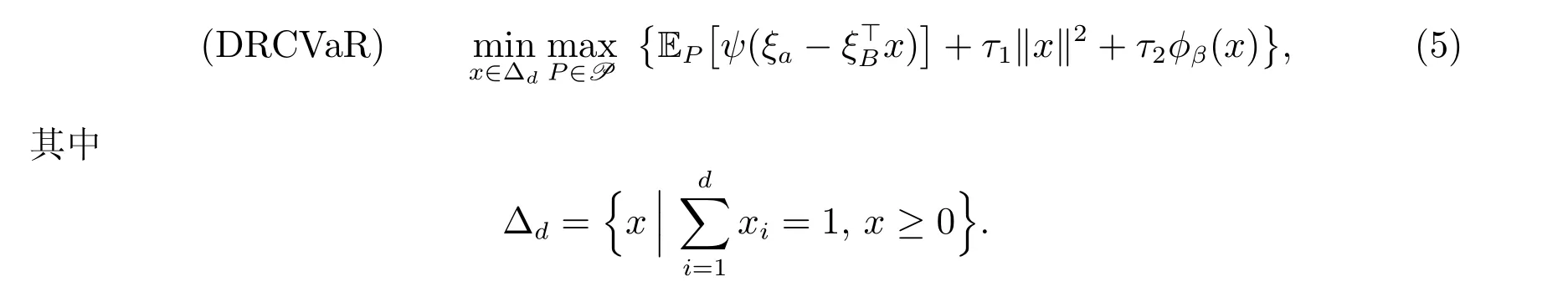


2 DRCVaR 易求解的等价转化模型
3 离散化方案

4 SPG 方法
4.1 光滑化函数
4.2 光滑投影梯度(SPG)方法


5 数值结果




6 结论
