大模数齿轮齿条副剥落故障啮合刚度分析*
2024-01-03陈保家盛洪潇肖文荣
陈保家,盛洪潇,万 刚,肖文荣
(1.三峡大学水电机械设备设计与维护湖北省重点实验室,宜昌 443002;2.中国长江电力股份有限公司,宜昌 443002)
0 引言
齿轮齿条机构可以实现由圆周运动向直线运动的传递,由于其具有传动效率高、承载能力强、结构紧凑等优点,多用于大型起升设备的关键升降装置,在大型矿山机械、港口平台中得到了广泛应用。三峡升船机作为大国重器,采用的是开式大模数齿轮齿条传动的爬升方式,是目前世界上运行条件最复杂、技术难度最高、建设规模最大的升船机[1],系统组件之间的相互耦合性日益增强,服役环境和运行工况日趋复杂[2]。
大模数开式齿轮齿条机构具有提升距离长、提升吨位大、体积结构大以及运行可靠性高的优点,由于长期受到低速、重载、往复、交变的载荷作用,直接暴露于空气条件下,会加速引发齿面出现细微的疲劳裂纹,这些细微裂纹会逐步扩宽和延伸,致使齿面发生点蚀或剥落故障,引发传动系统出现振动异常,从而降低齿轮齿条传动系统的可靠性。剥落故障是大模数齿轮齿条传动系统的常见损伤形式之一,一旦发生轻则引起系统的振动异常,严重时甚至会导致传动失效,对其传动副刚度研究是了解故障特征、揭示故障机理的重要研究方向。当齿轮发生齿面剥落故障时,由轮齿时变啮合刚度引起的系统动力学响应特征可以作为故障诊断的重要依据[3]。近年来,国内外众多学者对剥落故障齿轮的啮合特性及时变啮合刚度开展了不同程度的研究,赵树滨等[4]用势能法计算剥落故障条件下直齿轮的时变啮合刚度,分析了剥落参数对时变啮合刚度的影响。李金锴等[5]运用Abaqus软件构建了斜齿轮啮合的有限元模型,根据单齿啮合刚度推导了多齿啮合刚度变化,并结合动力循环实验台进行了疲劳点蚀实验验证了时变啮合刚度和齿轮动态响应之间的关系。涂旭欣等[6]考虑了多种剥落形状对直齿轮时变啮合刚度的影响,并结合动力学仿真与时频域分析讨论了剥落故障对齿轮动态特性的影响。林腾蛟等[7]提出一种裂纹故障斜齿轮时变啮合刚度改进算法,建立了传动系统耦合动力学模型,与相关文献方法和有限元方法进行了对比分析。LUO等[8]提出了一种新的直齿轮动力学模型,结合时变啮合刚度、齿间载荷分配、有限元网格阻尼比等考虑了点蚀和剥落引起的表面粗糙度的影响,并结合实验验证了理论模型的准确性。WU等[9]考虑到实际剥落形状的不规则性,提出了一种利用微元法计算斜齿轮不规则剥落形状的算法,并与有限元法进行了对比,验证了该方法的准确性。
总结上述研究工作,发现对啮合刚度的研究主要是针对常规齿轮啮合的情况,对齿轮剥落故障动力学分析较少,缺乏对大模数齿轮齿条副啮合刚度计算模型的全面研究。准确计算齿轮齿条副时变啮合刚度对分析齿轮齿条副传动系统动态特性、了解故障特征、揭示故障机理非常重要,因此,本文以三峡升船机齿轮齿条传动系统作为研究对象,搭建了大模数齿轮齿条升船机起升实验平台,对正常和剥落故障齿轮齿条机构的啮合过程进行了模拟分析,研究了剥落长度、剥落宽度、剥落深度、剥落位置对齿轮齿条啮合刚度的影响,并通过有限元法验证了大模数齿轮齿条时变啮合刚度计算的有效性。
1 大模数齿轮齿条实验台
为了对不同工况条件下的齿轮齿条啮合过程进行运行规律以及运动学响应特性,搭建了大模数升船机升降模拟实验台,其结构如图1所示。
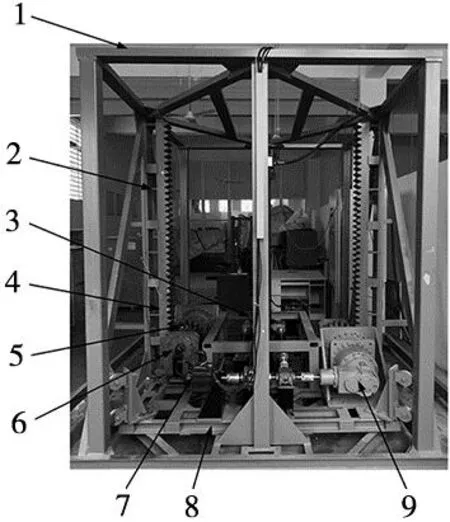
1.外形框 2.齿条支撑柱 3.液压加载装置 4.立式齿条 5.传动齿轮组 6.转速转矩传感器 7.驱动电机 8.升降平台 9.斜齿轮减速箱图1 实验台结构图
实验系统中,两套齿轮齿条式传动装置对称安装于升降平台上,两套驱动变频电机通过联轴器分别与斜齿轮减速箱负载端相连接,为齿轮齿条传动装置提供输入动力,又通过同步轴系统对两套齿轮齿条装置进行刚性联接,实现机械和电气同步控制,从而减小升降台运行的水平误差。液压油缸通过联轴器与斜齿轮减速箱负载端相连接,可模拟升船机的不同工况来对升降平台施加拉压力作用。PLC智能测控柜通过调节变频电机的转速可达到对齿轮齿条装置转速的控制,利用转速转矩仪反馈的信号对电机的运行进行监测,保持转速在设定的数值,通过压力传感器监测液压油缸的运行情况,保证所施加负载的稳定性,可实现实验台的远程操控,保证了实验现场的安全性。
考虑到三峡升船机齿轮齿条副设计的相关参数,本文采用以小推大的思想[10],设计了本实验台的齿轮齿条参数如表1所示,材料参数如表2所示。

表1 齿轮齿条的设计参数

表2 齿轮齿条的材料参数
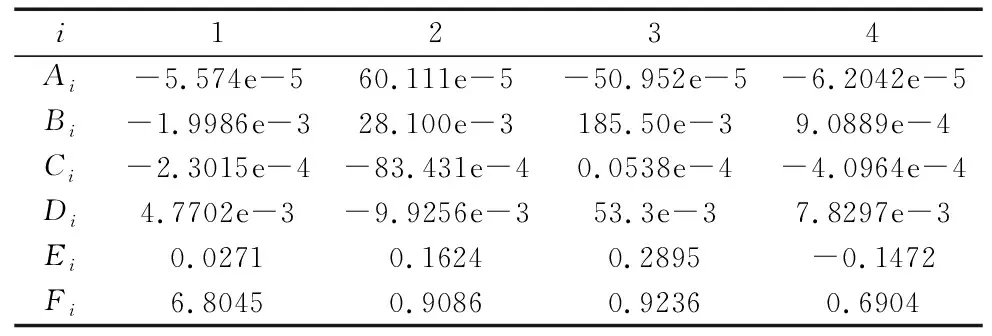
表3 拟合二项式系数

表4 系数
2 正常齿轮齿条副时变啮合刚度计算
齿轮啮合刚度表征齿轮啮合传动时抵抗变形的能力,齿轮时变啮合刚度是由啮合齿数和轮齿接触位置的循环变化所产生的时变函数,是研究齿轮系统动力学响应的重要方法,准确有效地计算出时变啮合刚度有利于更好的了解齿轮系统的动力学特性[7]。
将直齿轮啮合刚度定义为单位齿宽上的法向载荷与齿面变形量之比[11],其理论计算式为:
(1)
式中:Fn为作用于齿廓上的法向载荷,δ为齿面法向上的总变形量,b为齿轮齿宽。
本文将采用能量法计算齿轮刚度,将齿轮视为齿根上的变截面悬臂梁模型[12],轮齿悬臂梁模型如图2所示。

图2 轮齿悬臂梁模型
将材料力学变形理论与弹性力学势能计算原理结合即可得到啮合力F与总弹性势能U以及刚度K之间的关系式[13]为:
(2)
齿轮在啮合转动时,可将轮齿的总变形分解为切向变形、径向压缩变形、剪切变形、柔性基体变形以及接触面耦合产生的赫兹接触变形5个部分[14]。可通过势能原理式(2)得到弯曲势能Ub、剪切势能Ua、压缩势能Us,建立了刚度与势能之间的关系式:
(3)
由悬臂梁变形原理同样可得到上述3个分量的计算式:
(4)
式中:M为距离悬臂梁底部x位置的宽度为dx的矩形截面力矩,Fb和Fa分别为啮合力F水平方向和竖直方向的分力,k为截面比例系数,渐开线直齿圆柱齿轮为矩形截面,故k取值为1.2;G和E分别为材料的剪切模量与弹性模量,可由式(5)计算;Ix为距离悬臂梁模型底部x处的截面惯性矩,Ax为距离悬臂梁模型底部x处的截面面积,由式(6)计算[12]。
(5)
(6)
M=xcosα1-hsinα1
(7)
式中:υ为泊松比,b为齿轮宽度,hx为dx处齿厚的一半,根据直齿圆柱齿轮齿厚与弦长之间的关系可计算hx的值,计算式为:
(8)

由式(3)~式(8)联立可求得轮齿的弯曲刚度Kb、剪切刚度Ks和轴向压缩刚度Ka,表达式为:
(9)
式(9)以距离悬臂梁底部距离x为积分变量,与渐开线直齿轮齿廓建立的几何关系式较为复杂,不利于计算,所以,考虑到以转角α为积分变量,与齿廓曲线的换算关系简单、方便计算,根据几何关系,将上述以x为自变量推导的相关参数(d、h、hx和dx等)转换成角度α的函数:
(10)
至此,完成了将自变量距离固定端x转换成其相对应的圆心转角。将式(10)带入式(9)可推导出以转角α为积分变量的变限积分函数,各个刚度分量的表达式如下:
(11)
齿轮运行时,除了会产生以上刚度外,还包括赫兹接触刚度kh和轮齿基体柔性刚度kf,Hertz接触基本原理指出,可将由同种材料构成的弹性压缩体接触视为两抛物线相接触,得到的结果与实际值的误差控制在0.5%以内[15],可以得到,齿轮赫兹接触刚度kh实际上是仅与材料参数相关的常数,表达式为:
(12)
可以看出,kh只会随着齿轮宽度和材料参数的变化而变化,在齿轮啮合过程中为常数。由式(1)可知,轮齿基体柔性等效刚度的定义式为:
(13)
式中:δf为基体部分变形,计算式为:
(14)
式中:uf、Sf含义如图3所示,uf为啮合点延长线与齿轮中心线的交点o到齿根圆的距离,Sf为单齿对应的齿根圆弧长,可由式(15)计算得到:

图3 基体变形参数
(15)
L*、M*、P*、Q*可由如下多项式函数逼近得到:
(16)
式中:hfi=rf/rint。系数Ai、Bi、Ci、Di、Ei、Fi可根据文献[14-16]计算得到。
由式(13)~式(16)联立计算可得kf表达式为:
(17)
齿轮齿条副单轮齿啮合刚度由上述5个刚度分量综合得到,计算式为:
(18)
式中:下标1和2代表齿轮和齿条。
齿轮多齿啮合刚度为单齿啮合刚度的叠加过程,如图4所示,计算式为:
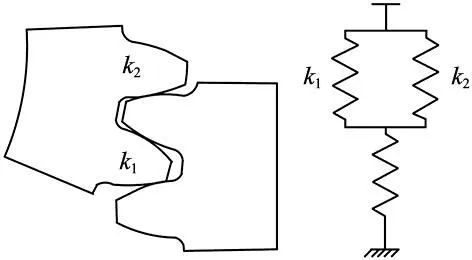
图4 多齿啮合过程及刚度示意图
(19)
式中:i=n代表第n对轮齿啮合。
齿轮齿条的啮合过程实际上是单齿-多齿-单齿的交替啮合过程,在齿轮齿条啮合传动过程中,前一对齿廓尚未完全脱开啮合时,后一齿廓已经开始进入啮合[12],因此需要考虑各个阶段开始和结束的临界啮合点。需要计算齿轮齿条的啮合重合度,如图5所示,N1N2为理论啮合线,B1B2为实际啮合线,根据重合度定义式(20)以及外啮合直齿轮重合度的计算公式(21)可推导齿轮齿条啮合的重合度公式:

图5 齿轮齿条重合度计算 图6 齿轮齿条啮合过程示意图
(20)
(21)
(22)
图6为齿轮齿条啮合的示意图,B1B2为齿轮齿条实际啮合线,根据几何关系:
(23)
(24)
由式(20)~式(24)可得:
(25)
式中:z1和z2为两齿轮的齿数,pb为齿轮基距,其余参数如图6所示。可以得到,ε=1.747 8,单齿啮合区间为:
(26)
将单齿啮合区间分为n=20份,对所得结果进行逐点计算可得到单齿啮合刚度,然后对单齿啮合刚度左右平移即可得到时变啮合刚度,结果图7所示。
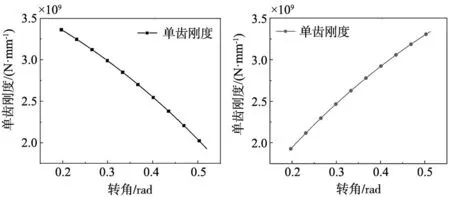
(a) 齿轮单齿刚度 (b) 齿条单齿刚度
3 剥落故障齿轮齿条副时变啮合刚度计算
齿轮齿面剥落通常是由于工作载荷过大、润滑不足、长时间往复运行等原因导致齿面疲劳损伤而引起的一种常见的齿轮齿面缺陷[17-18]。剥落故障的出现会严重影响齿轮传动的平稳性与可靠性,其动力学仿真对于了解齿轮系统的动力学行为和相应的故障振动特征具有重要意义[19]。
在齿轮齿条传动系统中,剥落通常发生在齿轮上(齿轮在工作中经历更多的旋转,所以会发生更多的应力循环),假设剥落区域尺寸参数为w、l、h,剥落简化示意图如图8所示,w为剥落宽度、l为剥落长度、h为剥落深度,剥落齿轮齿条副的接触模型如图9所示。当齿轮不存在故障时,接触线理论上为与齿轮轴平行的一条直线,当发生剥落故障时,由于材料从齿面移除,在缺陷处的接触线长度变短,相应的轮齿截面惯性矩和齿面截面积将变小;需要重新求解之后再代入刚度计算公式,计算公式同样采用第2节中使用的能量法,剥落齿轮悬臂梁模型如图10所示。

图8 剥落示意图
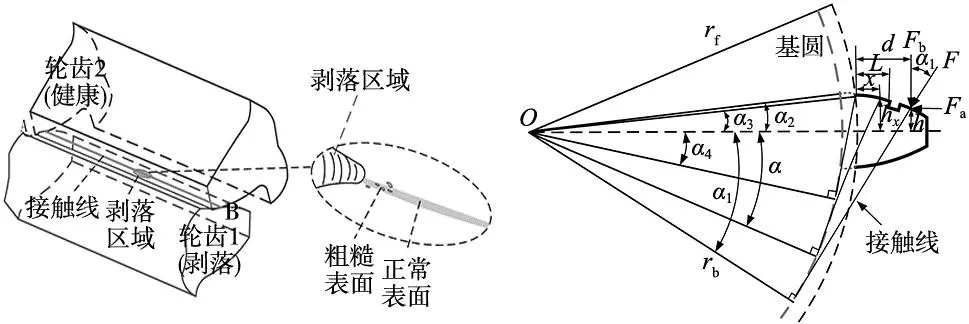
图9 剥落齿轮齿条副啮合模型 图10 剥落齿轮悬臂梁模型
计算齿面剥落齿轮的刚度时,应当考虑接触线长度、截面积和截面惯性矩的变化,分别可表示为:
(27)
将上式代入正常齿轮刚度计算公式即可得到剥落故障齿轮刚度计算公式。
(28)

(29)

(30)
式中:αs1和αs2分别为剥落起始和剥落终止对应的啮合角度,其求法与单齿啮合区间类似。本文设置的不同剥落故障尺寸参数如表5所示,以不同的剥落长度(沿齿高方向)表示3种不同的剥落故障严重程度。

表5 齿轮剥落尺寸参数
剥落位置位于齿轮节线与齿轮中心线交点处,设置剥落深度hs=2 mm,剥落长度为ls=5 mm的情况下,不同剥落长度的单齿啮合刚度如图11所示,可以看出,剥落齿轮相对于健康齿轮在剥落区域啮合时会出现刚度缺损,且在进入和离开剥落区域瞬间会出现刚度突变,随着剥落长度的增加,齿轮受剥落作用的影响时间越长,但不会影响刚度缺损的严重程度。剥落故障时变啮合刚度如图12所示,可以看出,刚度缺失主要是出现在单齿啮合区间及双齿啮合区,齿轮啮合是单双齿交替啮合的过程,在单齿啮合区间,齿轮刚度较小,抵抗变形的能力较弱,齿轮承受载荷更大,所以容易出现剥落故障,在单双齿交替时,会出现载荷冲击,所以在双齿啮合区域也会出现刚度缺失。

图11 不同剥落长度单齿综合刚度图
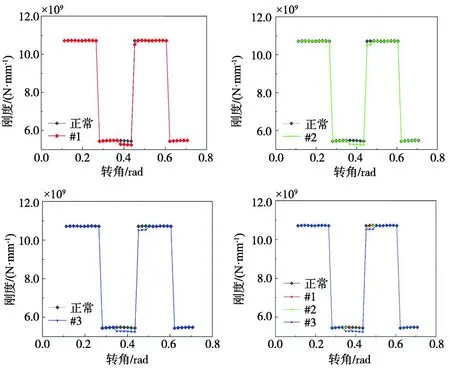
图12 不同剥落长度时变啮合刚度图
4 有限元分析
计算齿轮时变啮合刚度的另一种常见方法是有限元法,本节使用有限元分析对正常及剥落故障齿轮的时变啮合刚度进行计算,将结果与解析计算方法进行比较,用于验证解析方法的有效性材料参数的设置如表2所示。考虑到齿面之间的接触及接触力学的相关知识,为保证计算结果的准确性,需要对接触齿面网格进行细化,定义接触区域网格大小为2 mm,其余部分网格大小设置为10 mm。由于齿轮的接触问题较为复杂,在单元类型的选择方面应综合考虑有限元计算的效率与精度,所以单元类型选择为在接触问题中表现更优的六面体一次缩减积分单元(C3D8R)网格单元[12],考虑到齿轮齿条的啮合为单齿-双齿的交替啮合过程,对有限元模型进行简化,最终保留三对齿进行计算,降低模型的计算量,最终的齿轮齿条有限元网格模型如图13所示。节点数为301 677,节点数为208 558,对齿条底部施加固定约束,齿轮轴孔处施加对地面的回转副。
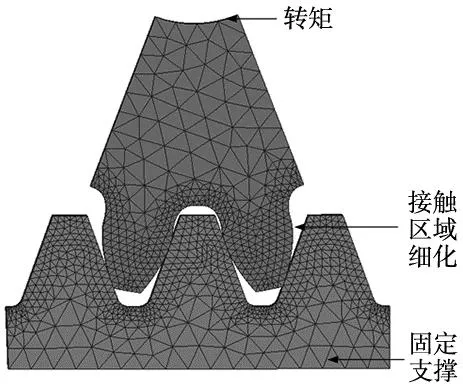
图13 网格划分结果
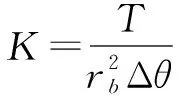
图14为正常齿轮解析法与有限元法所得单齿刚度与时变啮合刚度计算结果对比,可以看出,通过解析法计算的结果相比于有限元仿真计算所得结果偏大,误差为8%左右,但趋势基本相符,在一个齿的啮合过程中,齿轮刚度呈现递减趋势,齿条刚度呈现递增趋势,将单齿啮合刚度进行左右平移叠加即可得到综合啮合刚度,由综合啮合刚度图可知,齿轮在单齿啮合区间承载较大,刚度值较小;图15为3种剥落故障齿轮解析法与有限元法计算结果对比图,由图可见,解析法的计算是比较粗糙的,很多位置进行了简化处理,有限元法计算是细致局部的,结果更为准确。在啮合过程中,解析法与有限元法所得结果趋势上是一致的,齿轮齿条刚度对比误差如表6所示;从3种故障下的对比图可以看出,剥落长度越大,刚度缺损所占区间越长,且在啮出单齿区间时,由于齿轮齿条之间产生了严重啮合冲击,啮合刚度会出现突增;同时,还可以看出误差最大值出现在啮出单齿区间时,原因是未考虑到齿轮啮出单齿区瞬间产生冲击及剥落边缘效应,此有限元模型未能诠释出啮出瞬间的特殊性,在后续的工作中,可以考虑对此进行改进。

表6 剥落齿轮刚度误差表
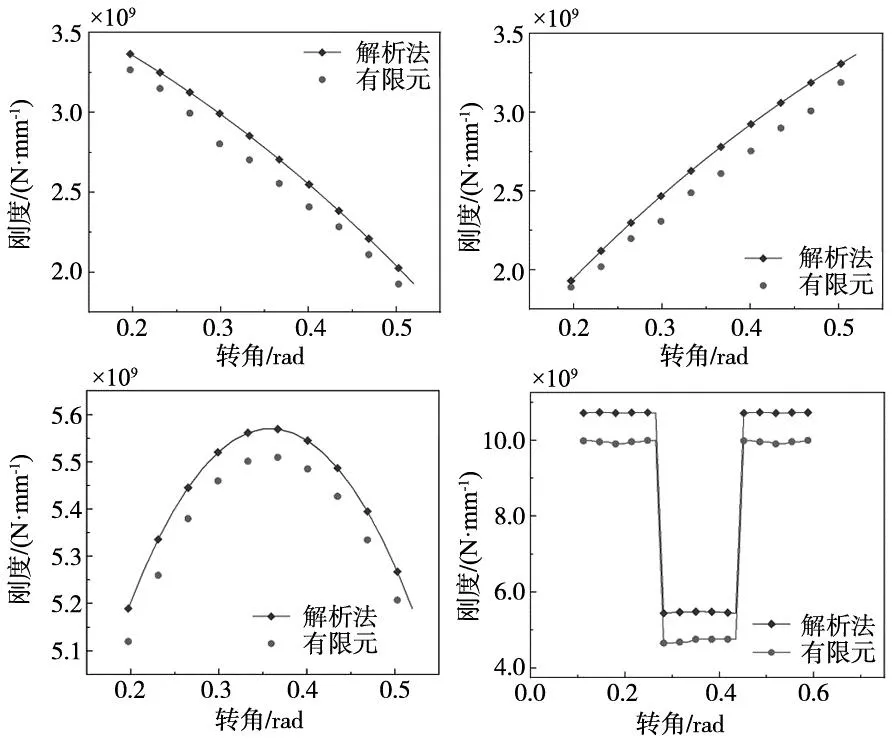
图14 正常齿轮刚度对比

图15 故障齿轮刚度对比
5 结论
从能量法的计算原理出发,利用大模数齿轮齿条传动副,并建立有限元模型进行了正常和剥落故障齿轮啮合刚度分析,可以得到如下结论:
(1)利用能量法计算得到正常齿轮齿条副的啮合刚度,并与仿真计算所得结果进行比较,误差在9%左右,验证了理论计算的正确性。
(2)推导了齿轮剥落故障的刚度计算公式,结果表明,剥落故障会引起轮齿啮合过程中的刚度缺损。
(3)建立了3种尺寸的齿轮剥落故障,结果表明,解析法与有限元法计算结果吻合较好,随着剥落长度的增加,出现刚度缺损的区域越大,且误差最大值出现在单齿啮合区域,原因是轮齿承受载荷更大且在单双齿交替啮合时会产生啮合冲击。
