基于A*算法与组合函数的分拣机械臂轨迹规划*
2024-01-03王成军姚星宇
王成军,姚星宇,杨 林,丁 凡
(安徽理工大学 a.人工智能学院 b.机械工程学院,淮南 232001)
0 引言
在智能化铸造生产线上常需要采用六轴工业机械臂完成上下料以及分拣的工作任务。铸件分拣机械臂工作前必须对机械臂的末端轨迹进行规划,使其可在有障碍环境下,执行分拣操作。常用的路径规划算法在动态环境和静态环境下用法不同。在静态路网中主要是以Dijkstra算法和A*算法为主[1],Dijkstra算法其实质为广度优先搜索,因为这种算法不能确定目标点的位置,需朝着所有可能方向遍历大量节点,导致工作效率低下,而A*实际上是一个带有启发性Dijkstra算法,由于引入启发函数,遍历节点时更具有一定目的性,遍历的中间节点更少,算法效率更高[2]。
针对传统A*算法路径规划速率低、耗时长的问题,邹文等[3]提出一种融合改进A*算法与动态窗口法的路径规划算法,实现了快速规划出一条折点少、耗时短的最优全局路径。高扬等[4]通过引入克拉美-罗下界预测栅格定位方差的上界,设计新的代价函数,实现更高定位性的寻找最优路径。但是A*算法计算通常在栅格中,得到的轨迹在速度、加速度上不连续,且轨迹不平滑对机构也会产生冲击振动问题,廖志炜等[5]针对此类问题提出一种通过摆线函数和矩形函数相结合的方法,减小加速度所带来的冲击。张玲[6]基于三次非均匀B样条曲线,通过曲线连续性对所求路径逼近,成功减小加减速在运行过程中的振动问题。但是目前将算法最短路径和平滑轨迹相结合,针对于工业用六轴机械臂轨迹规划的研究较少。
本文在对六轴分拣机械臂模型进行运动学分析后,采用A*算法规划一条从起始点到目标点的最短路径,在所得出的路径基础上与组合函数相融合得到平滑轨迹,并与常用五次多项式插值函数模拟仿真对比分析,确保在组合函数形式下的轨迹规划,机械臂能稳定、平滑的运行。
1 机械臂运动学分析
以ER20-C10六轴分拣机械臂为研究对象进行运动学分析,为控制末端执行器的运动位置,需要建立末端执行器和基座之间的关系坐标矩阵,需要在各个关节上建立坐标系,采用Modified DH参数法[7]对分拣机械臂建立坐标系,如图1所示。

图1 六轴分拣机械臂连杆坐标系
得到相应的DH参数表如表1所示。表中i为连杆序号;di为沿着Zi轴方向,Xi-1轴与Xi轴之间的直线距离;ai-1为沿着Xi-1轴的方向,Zi-1轴和Zi轴之间的距离(ai>0);αi表示从Xi-1轴的方向看,Zi-1轴和Zi轴间的夹角;θi表示从Zi轴的方向看,Xi-1轴和Xi轴间的夹角。
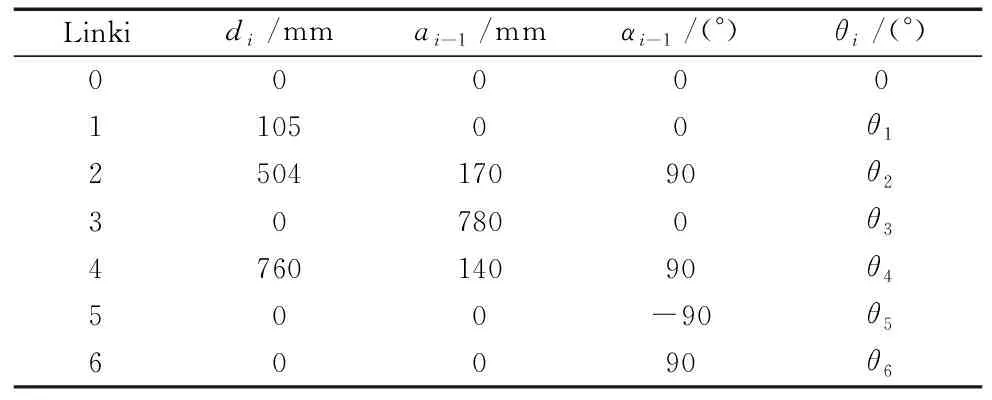
表1 六轴分拣机械臂的DH参数表
1.1 正运动学分析
运用DH参数法可得到初始位置的齐次变换矩阵,相邻两连杆的变化矩阵公式为:
(1)
基于表1的DH参数,得到各连杆的变换矩阵:
(2)
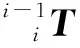
(3)
式中:[r11,r21,r31]T,[r12,r22,r23]T,[r31,r32,r33]T代表末端执行器x,y,z的方向向量,[Px,Py,Pz]T代表末端执行器的位置向量。
1.2 逆运动学分析
由正运动学可得到分拣机械臂末端位姿,而将末端执行器的位置控制转换为关节空间的角度控制,需要对分拣机械臂求逆解,一般所求的逆解不唯一,通过对比各关节的运动参数依次排除可得到正确的角度。
六轴分拣机械臂前三轴能确定腕部中心的位置,后三轴能确定末端执行器的姿态,其腕部和姿态可相互解耦,用代数法[8]求解前三轴,根据机械臂的特点可得到:
(4)
(5)
(6)
计算0P4ORG坐标平方和,用r表示,采用换元法消除关节角θ1,在a1≠0,sα1≠0的情况下得:
(7)
(8)
代入r中可求解出θ2θ3,θ4θ5θ6后三轴交于一点由姿态决定,数值可由欧拉角公式和旋转矩阵求出[9]。
2 A*算法路径搜索
2.1 A*算法
A*算法是一种用于静态网路中取路径最优最有效的一种启发式搜索方法。其算法核心是在最佳优先算法和Dijkstra算法(广度优先)基础上[10],添加heuristic启发式函数。采用A*算法路径搜索时,每遍历一点都会通过估算当前位置到最终目标点的代价来判断路径的优劣,将估算函数值较小的作为下一点,直到到达目标点。A*算法的路径优劣评价公式[11]为:
f(n)=g(n)+h(n)
(9)
式中:f(n)表示从路径通过初始点到中间点n最终到达目标点的代价估计,g(n)表示路径从初始点到中间点n的代价估计,h(n)表示路径从中间点到达目标点的代价估计。A*算法路径搜索前需定义两种列表openlist表和closedlist表,将待考察的点放入openlist表中,已经遍历过的,或离自身距离为0的点放入closedlist表。路径评价中h(n)估算函数的设计较为重要,若h(n)总是较小,此时A*算法能确定找到最短路径,但是遍历的节点也会增加,导致openlist表中节点过多,降低算法的速度。若h(n)等于中间点n到目标点的代价,此时最优,能找到最优路径的同时且速度最快,所以设置一个合适的h(n)可以影响整个A*算法的效率。本文采用的启发式函数h(n)可根据欧式距离函数进行计算,即:
(10)
式中:xp,yp,zp为当前点的坐标,xg,yg,zg分别为目标点坐标,cP为当前点的路径代价。
本文对三维空间节点离散化分析,得到许多个离散点,通过启发式函数估算结束后,选出子节点,再以子节点为父节点逐渐靠近目标点。根据计算的启发函数可使遍历带有一定方向的朝目标点步进,而不用完全遍历所有空间节点。
2.2 障碍物建立与避障实现
机械臂在实际工作环境中,障碍物的外形各异,为了方便模型模拟,采用较为常规、规则的空间集合体建立障碍物模型。障碍物模型中心坐标为A(x1,y1,z1),半径为r1球形物和中心坐标为B(x2,y2),半径为r2,高度为h的圆柱体。通过简化模型,降低了计算难度,提升了算法效率,且所设障碍物大小较小,确保了机械臂模拟运动可行性。
为了实现避障,采用同样计算距离的方式,采用欧几里得距离公式,避开球形障碍物时,通过反复循环计算子节点与球心坐标之间的距离实现[12]。避开圆柱形障碍物时,在循环计算子节点XY轴坐标与圆柱距离的同时且比较Z轴坐标与圆柱高度,就可判断是否发生碰撞,其公式表达为:
(11)
式中:x1、y1、z1为球形障碍物中心坐标,r1、r2分别为球半径和圆柱障碍物半径,x2、y2为圆柱中心坐标,h为圆柱高度。
3 三次样条插值函数
A*算法求出的轨迹,虽然路径距离最短,但结合实际机械臂操作存在轨迹不够平滑、角度难以实现,以及速度、加速度不连贯的问题。通常这些问题容易导致机械臂损伤,需要着重考虑。先对轨迹进行平滑,通过A*算法的父子节点遍历,把所取最优路径点放入所设Openlist列表中,节点间直线相连形成轨迹。
对求出的轨迹进行平滑处理,一般常采用曲线插值的方法得出曲线的方程,但该种方法通常需要已知节点间的速度、加速度条件,而现已知条件只有通过的插值点,需要定义一条平滑曲线,则采用均匀三次B样条曲线[13]进行平滑。
B样条曲线方程:
(12)
式中:p(u)为B样条曲线函数,di为控制顶点,Ni,k(u)(i=0,1,…,n)为第k次规范B样条基函数,n为插值点个数,控制点个数为n+2,u为函数的参数轴,则整个B样条方程就是在序列U:u0≤u1≤…≤ui+k+1所有k次分段多项式组合而成,通过控制点来影响曲线绘制。所用的均匀B样条曲线,其任意节点区间的B样条基在大的参数轴下都可由另一节点上的B样条基平移得到,故可将[ui,ui+1]上整体参数u变换成局部参数t,做简单参数变换。
u=u(t)=(1-t)ui+tui+1,t∈[0,1]
(13)
则B样条曲线方程变为:
(14)
可得出三次均匀B样条曲线方程的矩阵形式:
(15)

图2为A*算法所求得的路径图,图3为采用三次均匀B样条函数对轨迹进行平滑后的图像,可看出融合了三次均匀B样条后的轨迹已经相对平滑。
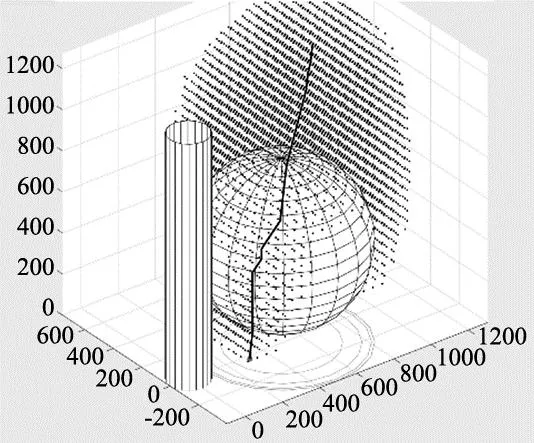
图2 A*算法最优路径轨迹图
4 基于组合函数的轨迹规划
为保证运行过程中速度、加速度连续性在多个运行阶段不出现较大波动,确保分拣机械臂工作的平稳性,启动阶段和停止阶段不能存有冲击,先采用摆线函数拟合,以速度、加速度及位置变量为约束条件,设加速度变量随时间周期变化的函数方程为:
(16)
积分得其速度函数方程:
(17)
边界约束条件:
(18)
设置组合函数,将摆线函数速度、加速度峰值降低,平滑过渡将整段运动时长分为8段,其中1/4周期的加速度值为矩形函数值,重新设置放大参数,得组合函数拟合关系式[14]:
(19)
对上式进行积分,代入边界条件可得速度与时间的变量函数:
(20)
通过上述分段函数积分求出轨迹线的关节角函数:
(21)
带入根据轨迹约束得:
(22)
为研究组合函数拟合曲线与五次多项式插值拟合曲线的优异性,需要具体的函数图像进行比较,将所优化轨迹和未优化轨迹的点带入到由DH参数表建立的MATLAB六轴机械臂模型中,采用机器人工具箱自带的五次多项式插值模拟仿真得到其动力学参数图。图4为MATLAB模拟仿真图,图5为关节角位移对比图,图6为关节角速度对比图,图7为关节角加速度对比图。
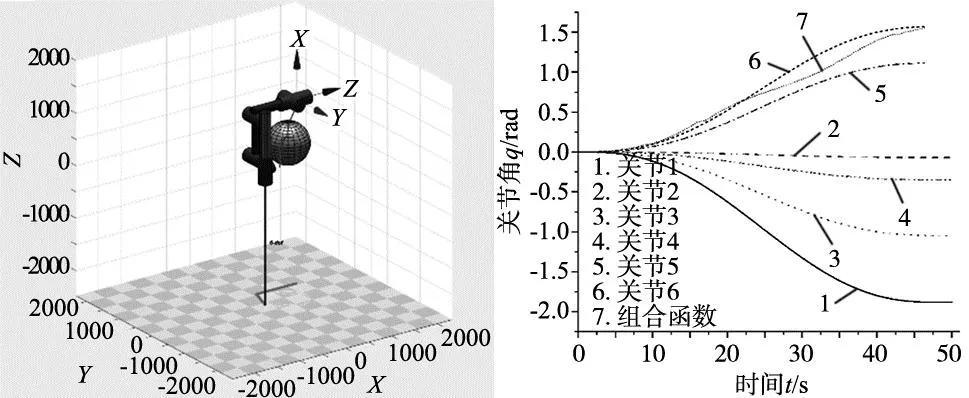
图4 机械臂末端轨迹模拟仿真图 图5 关节角位移对比图

图6 关节角速度对比图 图7 关节角加速度对比图
由图5可知,所拟合过的组合函数轨迹图与模拟仿真得出的关节角轨迹相差不大,从曲线波动来看25 s时位移突变较大,之后逐渐趋于平稳。从极值来看组合函数的位移数值基本不大,相对来看较为稳定。
由图6可知,五次多项式插值求出的角速度关节1、2、3波动幅值较大,其幅值按关节顺序逐渐减小,关节1幅值最大约为3 rad/s,关节6幅值最小,不超过0.2 rad/s,相对来看,组合函数的曲线波动更为稳定,曲线更为平滑。在运行周期的启停阶段除后3个关节外,组合函数的曲线均更为平缓,速度增长更平稳,关节处所造成的冲击更小。
由图7可知,所设置的组合函数具有较好的连续性,其1/4周期矩形部分很好地限制了关节的最大加速度和最小加速度,且相较于五次多项式插值得到的所有关节角加速度,就幅值和波动来看曲线变化基本一致。在设置良好的放大系数后,组合函数的峰值被稳定在6.4 rad/s2,对机械臂而言加速度越大,所造成的惯性力越大,对机械臂的运动、工作效率影响也越大,故所设组合函数更优,且在峰值部分与五次多项式插值函数对比,维持时间更长,工作效率更高。关节3、4为小幅精度调节运动,增长速度较缓,关节3、4的增长幅度与组合函数增长幅度大相径庭,从而所设计的组合函数对机械臂稳定运行有着良好的影响。
5 结论
针对所用铸件分拣的机械臂轨迹规划难题,通过采用A*算法,设置三维节点反复遍历,利用启发式函数获取搜寻方向,寻最短、最优路径,路径点间用直线段相连,形成轨迹。整体轨迹采用三次B样条对所得路径进行平滑处理,为保证机械臂运动过程平稳性,通过一种由摆线函数和常数函数相结合的组合函数对角位移、角速度、角加速度进行拟合,通过模拟仿真,得出仿真曲线图。由仿真结果可知,在启停阶段用组合函数拟合的关节角速度更为平缓,关节角加速度在加速与减速阶段增长趋势和减小趋势较小,且最大幅值保持时间维持约1/4周期,工作效率高。该轨迹优化方法可有效降低机械臂关节的最大和最小速度和加速度,从而减少了机械臂振动和惯性力的影响,且末端执行器轨迹最短,提高了机械臂工作效率。本研究为静态路径下的轨迹规划提供了研究基础。
