直线滚珠导轨库仑摩擦力建模与分析*

2024-01-03喻精辉张朋海

组合机床与自动化加工技术 2023年12期

喻精辉,张朋海

(重庆大学机械与运载工程学院,重庆 400044)

0 引言

直线滚珠导轨因其结构简单、成本低、精度高等优点在精密机床领域获得了广泛的应用[1]。对于导轨系统而言,非线性摩擦力是影响系统精度的重要因素,通常可以通过摩擦力补偿的方法减少或消除摩擦力的影响。

目前,主流的摩擦力补偿方法是基于摩擦模型的补偿[2-3],常用的摩擦模型有Stribeck模型、LuGre模型、Dahl模型等。CONG等[4]通过优化基于Stribeck模型的摩擦补偿策略,解决了由于摩擦力过度补偿引起的极限环,从而提高了系统精度。陈浩等[5]针对直线电机滑台的摩擦特性,提出了考虑加速度影响的二元Stribeck模型,并实验验证了模型的有效性。陈琳等[6]提出了一种修正Stribeck模型,缓解了传统Stribeck模型过补偿导致的过零处速度波动及跟踪误差大的问题。谭文斌等[7]修正了传统LuGre模型,并提出以修正模型为基础的补偿方案,提高了伺服系统的动态性能。JIANG等[8]基于LuGre摩擦模型建立了数字液压缸的数学模型,提出了一种自适应摩擦补偿控制方法,仿真结果表明该方法可有效降低系统静态误差、抑制系统极限回路振荡。彭洋等[9]提出了一种改进的Dhal摩擦模型,并研究基于该模型的摩擦补偿及参数辨识,结果表明该模型能有效提高系统动态性能。

然而,基于模型的摩擦补偿方案通常是建立在模型参数恒定或缓慢变化的假设上的,模型参数的改变可能会削弱补偿的有限性和充分性[10]。上述基于摩擦模型的补偿方法均将库仑摩擦力作为恒定参数引入模型,并未考虑库仑摩擦力波动导致的摩擦补偿不充分或失效。因此,针对系统库仑摩擦力建模,定量探究其波动情况,对提高摩擦补偿模型精度、保证摩擦补偿效果具有重要价值。本文仅研究库仑摩擦力的波动规律,库仑摩擦力波动对摩擦模型补偿效果的影响规律将在后续研究中补充。

本文将以双滚珠直线导轨四滑块结构平台为研究对象,考虑直线导轨的几何误差,建立库仑摩擦力分析模型,并分析库仑摩擦力的波动情况。

1 直线滚珠导轨系统模型

由于导轨几何误差的存在,滚珠的弹性变形会发生改变,系统将产生误差运动。为研究几何误差对导轨系统库仑摩擦的影响规律,本文将建立不同维度下的坐标系统,以滚珠变形协调关系为桥梁,建立各坐标系统下误差运动的映射关系和力学平衡方程,求解库仑摩擦力的波动情况。

1.1 坐标系统及几何误差

本文研究的双直线导轨四滑块系统采用对称布置,如图1所示。直线滚珠导轨副为四列对称结构,滚珠的初始接触角均为φ,导轨系统以速度u沿y方向运动,如图2所示。为建立导轨系统模型,以工作台与滑块连接平面的几何中心为原点建立导轨系统坐标系O-XYZ(如图1b、图1c所示);以滑块对称中心为原点建立滑块坐标系oi-xiyizi(如图2b所示),其中i为滑块编号,取值为1、2、3、4;以单列滚珠对称中心为原点建立滚珠列坐标系oij-xijyijzij(如图2a所示),其中j为滚珠列编号,取值为1、2、3、4;以单个滚珠几何中心为原点建立滚珠坐标系oijk-xijkyijkzijk,其中k为受载滚珠编号,取值为1、2…nb,nb为单列受载滚珠数。

(a) 左视图 (b) 俯视图

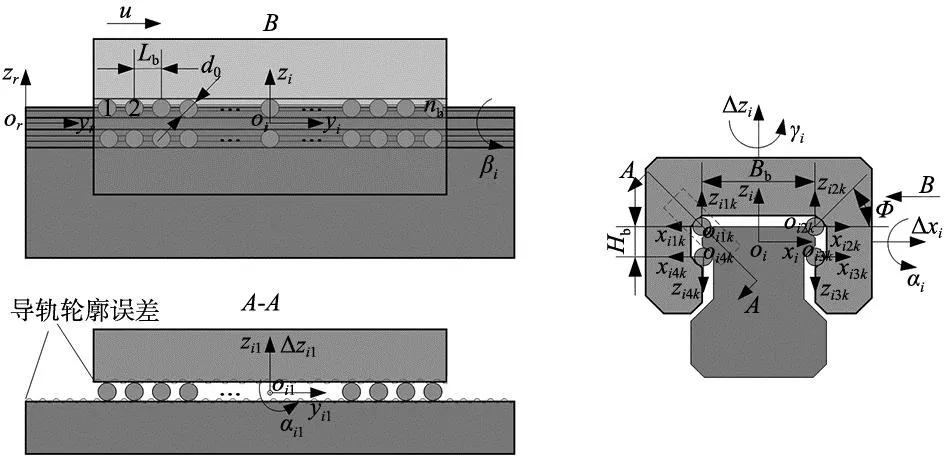
(a) 右视图与A-A剖视图 (b) 单滑块结构图2 滚珠直线导轨单滑块结构

根据傅里叶变换,复杂的几何误差可视为一系列正弦波的叠加,为了方便研究几何误差与误差运动的关系,本文将几何误差视为正弦波。导轨系统的几何误差主要由导轨的垂直变形误差(如图1a所示)、水平变形误差(如图1b所示)和滚道轮廓误差(如图2a所示)组成。为表示导轨的几何误差,在导轨对称平面上建立导轨坐标系or-yrzr,如图2a所示。这样滚珠ijk在导轨坐标系下的位置yr可表示为:

(1)

式中:Lb为相邻滚珠间距,Ls为同侧滑块中心距,d0为滚珠直径,s为系统在yr方向上运行的距离。

为直观地研究几何误差波长的影响,本文以相邻两滚珠间所包含正弦波数来表示波长,并根据波数大小将波长分为3个系列,即:长波长(波数在0.01～0.1之间),中波长(波数在0.1～1之间),短波长(波数在1～10之间)。这样,每个滚珠位置上的几何误差可表示为:

(2)

式中:ΔEp_ijk、ΔEdv_ijk、ΔEdh_ijk分别表示滚珠ijk位置上的滚道轮廓误差、垂直变形误差和水平变形误差,E、n、φ则分别表示几何误差的幅值、波数和初始相位,l为导轨编号,m为轨道编号,其数值与滚珠列号相同。

1.2 误差运动及映射关系

对于双轨四滑块系统O-XYZ,由于导轨几何误差等因素,系统会产生5个误差运动Δx、Δz、α、β、γ。对于单滑块系统oi-xiyizi,同样会产生5个误差运动Δxi、Δzi、αi、βi、γi。根据几何关系建立坐标系O-XYZ与坐标系oi-xiyizi(i=1、2、3、4)下误差运动的映射关系,如式(3)～式(6)所示。

(3)

(4)

(5)

(6)

式中:Bs为导轨轴线间的距离。

对于单列滚珠系统oij-xijyijzij,系统会产生误差运动αij和Δzij,而滚珠oijk-xijkyijkzijk则会产生沿接触方向的误差运动εm_ijk,此误差运动在xijk、zijk方向的分量为εm_ijk_x和εm_ijk_z。假设每个滚珠几何参数完全一致,且呈均匀分布,则坐标系oijk-xijkyijkzijk和oi-xiyizi下的误差运动间的映射关系为:

(7)

式中:Bb为左右两列滚珠间距,Hb为上下两列滚珠间距,L为滑块长度,f1、f2、f3为位置系数,与滚珠列的位置相关,定义为:

(8)

同理,可建立坐标系oijk-xijkyijkzijk与oij-xijyijzij下误差运动的映射关系:

(9)

自此,通过式(3)～式(9)建立起从单个滚珠到双导轨四滑块系统间误差运动的映射转换关系。

1.3 力学平衡方程

在滚珠直线导轨装配过程中,为了消除间隙,提高导轨刚性,通常需要施加预紧力F0。对于滚珠ijk,其法向接触力与预紧力平衡,即:

Fijk=F0

(10)

为了研究滚珠的变形协调关系,本文认为滚珠与滚道之间的受力变形均在弹性变形范围内,滚珠与两侧接触滚道的接触变形均由滚珠承担,滚道不发生变形[11],根据Hertz接触理论有:

(11)

式中:ε0为滚珠的预加载变形,εijk为滚珠的总弹性变形,K为Hertz接触刚度,可由下式计算[12-13]:

(12)

分别考虑导轨垂直变形、导轨水平变形、导轨滚道轮廓误差作用下的变形协调关系,由图3可得:

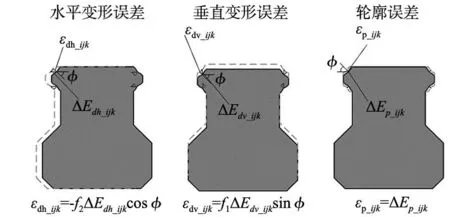
图3 导轨几何误差

(13)

对于滚珠列ij,在坐标系oij-xijyijzij下,力学平衡方程为:

(14)

对于滑块i,在坐标系oi-xiyizi下,力学平衡方程为:

(15)

对于双导轨四滑块系统,在坐标系O-XYZ下建立力学平衡方程为:

(16)

1.4 基于运动误差的库仑摩擦力计算

若导轨几何误差已知,可求解上文的方程组获得误差运动和滚珠弹性变形的大小,进而分析库仑摩擦力的变化情况。当系统运动时,将滚珠运动方向视为一致,则滚珠列ij库仑摩擦力等于该列所有滚珠摩擦力之和,即:

(17)

式中:μ为库仑滑动摩擦系数。同理,可计算滑块i和整个导轨滑块系统的库仑摩擦力:

(18)

(19)

库仑摩擦力与滚珠弹性变形状态相关,滚珠的变形状态会随导轨位置改变,精确计算导轨在每个位置下的库仑摩擦力是十分困难的。在摩擦补偿模型中,库仑摩擦力通常被视作常数,其均值部分可获得良好补偿,而波动部分却难以量化和补偿,但可通过减小其波动范围来提高摩擦补偿效果。因此,对库仑摩擦力波动范围的研究更具现实意义。

前文将导轨几何误差定义为正弦函数,在滚珠均匀分布的假设下,库仑摩擦力波动具有明显的周期性。因此,可用库仑摩擦力均化系数δ来量化库仑摩擦力的波动大小,其定义为运动周期内库仑摩擦力的幅值与其均值的比值,即:

(20)

2 讨论

2.1 参数

导轨的3种几何误差对库仑摩擦力波动的作用是叠加的,为了直观研究3种几何误差对库仑摩擦力波动的影响,在算例分析时仅考虑单一几何误差对库仑摩擦力波动的影响。

对于导轨变形误差,本文以右侧导轨(编号2)作为理想形状,仅分析左侧导轨(编号1)存在水平变形误差(或垂直变形误差)时库仑摩擦力的波动情况。

对于滚道轮廓误差,同一导轨上4条滚道的轮廓误差对系统库仑摩擦力的影响是矢量叠加的,可等效为4条滚道的轮廓误差矢量叠加后作用在任一滚道上,其余滚道视作理想形状。因此,本文以左侧导轨左上滚道(编号11)的轮廓误差为代表,分析导轨滚道轮廓误差对库仑摩擦力波动的影响。算例参数如表1所示。

表1 模型参数

2.2 单个滑块库仑摩擦力均化系数分析

当导轨1的水平变形误差波数ndh_1由0.01～0.1(长波长),0.1～1(中波长),1～10(短波长)变化时,滑块3的库仑摩擦力均化系数δ如图4所示。

图4 导轨1水平变形误差下滑块3的δ

对于短波长的水平变形误差,δ的变化存在明显的周期性:当ndh_1为整数1、2、3…时,δ取得最小值0,当ndh_1为1.5、2.5、3.5…时,δ取得最大值,并且在同一周期内,δ的变化关于ndh_1=1.5、2.5、3.5…对称。对于中波长的水平变形误差,当ndh_1=0.5时δ取得最大值,在该波数±0.03范围内的δ明显大于其它波数。同时不难发现,当ndh_1的取值为0.2～0.4和0.6～0.8时,δ在一个较低的水平下波动。对于长波长的水平变形误差,δ呈现随ndh_1的增加缓慢增加而后缓慢减少的趋势,当ndh_1=0.08时取得最大值。

导轨变形误差波长主要决定于其安装孔距,而安装孔距通常位于中波长范围内,将导轨安装孔距设计为2.5Lb～5Lb时可有效抑制库仑摩擦力的波动。由前文可知,库仑摩擦力波动来源于滚珠弹性变形的变化,同时弹性变形的变化会引起导轨误差运动的波动,且滚珠弹性变形变化越大,误差运动波动越大,库仑摩擦力的波动也越大。文献[14]已通过有限元方法验证了改变导轨安装孔距对误差运动波动抑制的有效性,这同时也间接验证了其对库仑摩擦力波动的抑制效果,本文不再重复验证。

如图5所示,当仅导轨1存在垂直变形误差时库仑摩擦力的波动情况与仅存在水平变形误差时相同,这表明导轨水平变形误差与导轨垂直误差对单滑块系统库仑摩擦力的影响没有本质区别。

图5 导轨1垂直变形误差下滑块3的δ

当仅导轨滚道11存在轮廓误差时,不同np_11下滑块3的库仑摩擦力均化系数δ如图6所示。对于短波长的滚道轮廓误差,δ存在明显的周期性和对称性,当np_11为整数1、2、3…时,δ取得最大值。对于中波长的滚道轮廓误差,当np_11=1时,δ取得最大值,且当np_11=0.95～1时,δ明显大于其它波数。对于长波长的滚道轮廓误差,随着np_11的增大,δ呈现先减小而后缓慢增大的趋势,并在np_11=0.085时取得最小值。

由图4和图6可知,在滚道轮廓误差下的δ比导轨变形误差下的大一个数量级,说明单一轨道轮廓误差对滑块库仑摩擦力波动的影响更大。这点可依据几何误差的特点来解释:对于导轨的变形误差,此导轨上四列滚珠的接触变形均会直接受其影响,如图3所示。导轨垂直变形误差对于上下两侧滚珠接触变形的影响相反,而水平误差变形则对左右两侧滚珠接触变形的影响相反。导轨两侧滚珠相反的接触变形影响会抵消部分变形误差引起的接触力变化,库仑摩擦力波动相对减少。对于滚道轮廓误差而言,它只会直接影响本列滚珠的接触变形,不存在多列滚珠的均化作用,库仑摩擦力的波动更大。

2.3 双导轨四滑块系统库仑摩擦力均化系数分析

当仅导轨1存在水平变形误差时不同ndh_1下双导轨四滑块系统的库仑摩擦力均化系数δ如图7所示。对于短波长的导轨水平变形误差,δ存在明显的周期性与对称性,且当ndh_1=1.5、2.5、3.5…时,δ取得最大值。对于中波长的导轨水平变形误差,当ndh_1取0.93、0.94、0.96、0.97时,δ的值会明显大于其它波数。与单滑块的情况类似,当ndh_1取值为0.2～0.4,0.6～0.8时,δ值一直维持在一个较低水平,将导轨安装孔距设计为2.5Lb～5Lb可有效减少库仑摩擦力波动。对于长波长的导轨水平变形误差,在计算范围内,δ随ndh_1的变化呈现近似的对称性,当ndh_1为0.037、0.066时,δ取得较大值。

图7 导轨1水平变形误差下双轨四滑块系统的δ

当仅导轨1存在垂直变形误差时,δ变化规律与仅存在水平变形误差时相同,如图8所示。

图8 导轨1垂直变形误差下双轨四滑块系统的δ

当仅导轨滚道11存在轮廓误差时,不同np_11下双轨四滑块系统的库仑摩擦力均化系数δ如图9所示。对于短波长的滚道轮廓误差,δ也存在明显随np_11变化的周期性和对称性,且当np_11为整数1、2、3…时,δ取得最大值。对于中波长的滚道轮廓误差,当np_11=1时,δ取得最大值,且在除np_11=0.95～1外的其它波数下,δ接近于0。对于长波长的滚道轮廓误差,滚道轮廓误差在np_11=0.017、0.05、0.08时取得最小值0,在np_11=0.031时取得最大值。

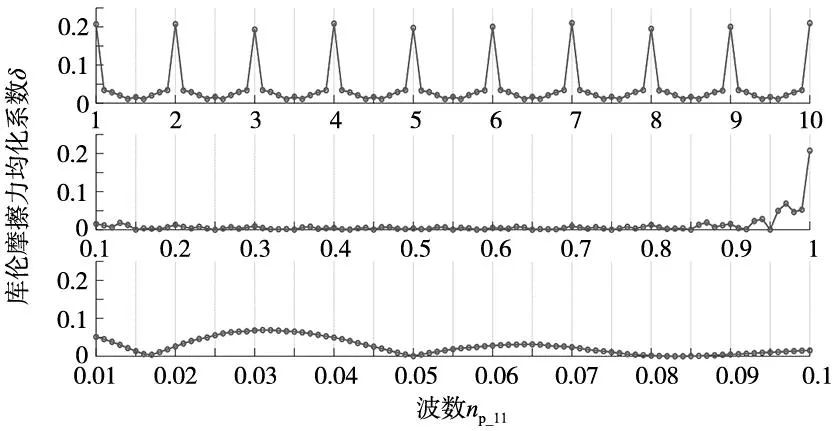
图9 导轨滚道11轮廓误差下双轨四滑块系统的δ

对比图7和图9可知,在滚道轮廓误差下δ比导轨变形误差下的大一个数量级,表明单一轨道轮廓误差对双轨四滑块系统库仑摩擦力波动的影响更大。与单滑块的情况类似,导轨滚道对变形误差的均化作用削弱了导轨系统库仑摩擦力的波动,而单滚道的轮廓误差则不存在这个均化作用,故库仑摩擦力波动更大。

2.4 库仑摩擦力均化系数影响因素分析

由前文可知,单滑块系统和双轨四滑块系统的库仑摩擦力均化系数δ存在相似的变化规律,且单滚道轮廓误差对δ的影响大于变形误差。因此,对滚道轮廓误差下单滑块系统δ的影响因素的研究具有良好的代表性,下文分别讨论此情形下几何误差幅值、预紧量对δ的影响。

当滚道轮廓误差幅值Ep_11为2.5 μm,其它参数相同时,导轨滚珠预紧量ε0为3 μm、5 μm和7 μm时δ的变化如图10所示。当滚珠预紧量ε0为5 μm,轮廓误差幅值Ep_11为2 μm、2.5 μm和3 μm时δ的变化如图11所示。对比两图可知,对于不同波长系列下的滚道轮廓误差,改变滚珠的预紧量或几何误差幅值均不会改变δ随np_11变化的趋势,且在相同波数下,δ随几何误差幅值的增加而增加,随预紧量的增加而减少。

图10 预紧量对δ的影响(导轨滚道轮廓误差)

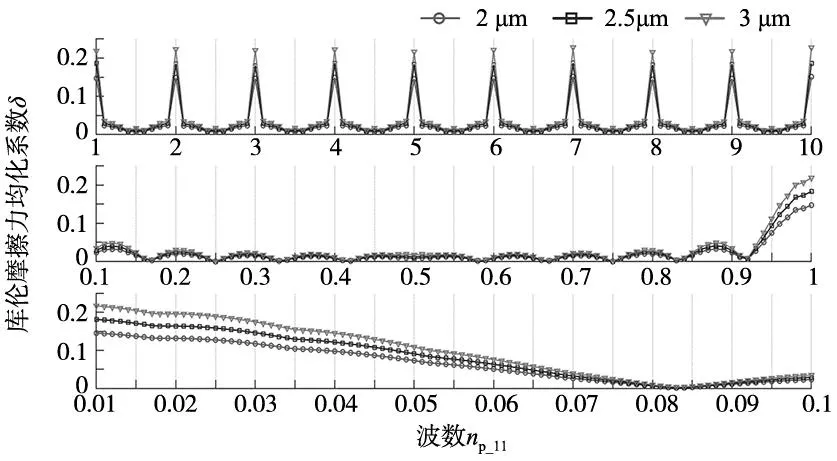
图11 几何误差幅值对δ的影响(导轨滚道轮廓误差)

以np_11=1为例,具体分析几何误差幅值Ep、滚珠预紧量ε0和库仑摩擦力均化系数δ的关系。由图10可知,当Ep_11=2.5 μm,ε0分别为3 μm、5 μm、7 μm时,δ分别为0.300、0.186、0.132。由图11可知,当ε0=5 μm,Ep分别为2 μm、2.5 μm、3 μm时,δ分别为0.147、0.186、0.218。对于以上两组数据,当np_11=1时,δ与Ep/ε0的比值均在0.36附近。对于其它组数据,当几何误差波数np_11确定时,排除部分异常值,δ与Ep/ε0的比值也是一个确定值。因此,当np_11一定时,可认为δ与Ep/ε0成正比,即δ=Kf_gEp/ε0,其中Kf_g为比例系数,与几何误差波数相关。在确定几何误差和滚珠预紧量的条件下,可据此预测系统库仑摩擦力的波动大小。同时,此关系表明了在应力允许的情况下,选择更大的预紧量可有效减少库仑摩擦力的波动。