低速巡航中车辆离合器转速跟踪控制技术

王国新

(福州大学 至诚学院,福建 福州 350002)

0 引言

随着智能传感器和环境感知不断进步,智能化、自动化、自动驾驶等智能车辆技术迅速发展,车辆行驶过程中的自动化控制也越来越受到关注[1]。对于智能化的自动驾驶车辆来说,自动变速器能够在行驶过程中自动换挡,不仅减小了司机的驾驶压力,也保证了车辆的安全性和平缓性。电控机械式自动变速器(automated manual transmission, AMT)加入了电控和自动执行单元,能够自动整合档位和离合器,在车辆驾驶过程中实现自动化控制。加入了电控技术,使AMT在自动执行换挡变速的过程中的车辆污染排放减少,提高了驾驶安全和舒适度[2-3]。所以,AMT的出现不仅迎合了国家“双碳政策”,在未来智能化、自动化和节能化的发展方向上具有更大的市场潜力和发展前景。

当AMT车辆面对特殊路况时,例如交通拥挤道路中的低速跟车行驶,车距较小,且挡位变化时间短,只有AMT实现良好的车速跟踪性能才能保证车辆安全和司机减压[4]。考虑到车速跟踪时的状态变换频繁,如果直接由发动机/变速箱输出动力,在低速巡航时很难实现稳定跟踪前车的性能;而如果要进一步精准跟踪车速,则需要来回切换离合器的分合状态,从而实现车辆的安全和稳定控制[5]。所以,低速巡航状态下,AMT车辆如何提高与前车的车速跟踪性能,即提高离合器的转速控制,这是目前急需解决的重要难题。

本文基于AMT车辆动力传动系统中的动力学特性,构建发动机、离合器和整车运动的数学模型,简化AMT传动系统,提出低速巡航中的离合器控制要求,通过Lyapunov函数对三步法控制器进行鲁棒性分析,最后通过改造车辆的实车试验对本文方法进行对比验证。

1 低速巡航动力传动建模

本文基于AMT车辆动力传动系统中的动力学特性,构建了汽油发动机、干式离合器和整车运动的数学模型,以实现AMT车辆在低速巡航中的精准速度跟踪[6]。

1.1 发动机模型

Te=f(ne,β)

(1)

(2)

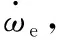
(3)

1.2 干式离合器模型

对于干式离合器,定义其压紧力Fc,离合器中的摩擦片单片摩擦因数为μ,内外半径分别为R和r,共有zc个,则摩擦片作用半径Rc为

(4)

则离合器分合过程中的动摩擦转矩Tc为

Tc=FcμRczc

(5)

1.3 整车模型

本文考虑到车辆的装载质量mc和整备质量mv,利用旋转质量换算系数δi将整车模型定义为车辆等效质量M,并综合车辆多种外力构建纵向动力学方程:

Ma=Ft-Ff-Fw-Fi

(6)

定义δi中Iw和If分别为车轮和飞轮的转动惯量,ig和i0分别为变速器速比和主减速器传动比,则M和δi分别为:

M=δi(mv+mc)

(7)

(8)

定义转动系统总效率为η,滚动半径为rd,在第n挡时的传动比为in,则车轮等效驱动力为Ftn:

(9)

定义道路滚动阻力Ff:

Ff=f(mv+mc)g

(10)

定义空气密度ρ和阻力系数CD,车辆迎风面积Aw和相对行驶速度u,则空气阻力Fw为

(11)

对于爬坡车辆,其爬升角即坡度角为αg,则沿坡道的重力分力定义为坡道阻力Fi:

Fi=(mv+mc)gsinαg

(12)

如果αg较小,则坡道阻力Fi可近似用路面坡度i表示为

Fi=(mv+mc)gi

(13)

2 三步法离合器转速跟踪控制器设计

2.1 控制问题

多挡位AMT车辆通过低速巡航中离合器滑摩控制行驶速度。换句话说,干式离合器只有在滑摩过程才能输出低速巡航的期望转速,如图1所示。因此,本文采用二质量系统以简化模型开发难度。

图1 动力传动系统简化模型

定义离合器传递转矩和输出转速分别为Tc和ωc,AMT车辆的阻尼和阻力转矩分别为Cv和Tl,整车车速和惯性系数分别为v和Iv,则传动系统简化方程为[8]

(14)

对于上式,由于行驶车速v需要跟踪前车车速v*,而前车车速v*需要通过雷达感知获取,因此设定v*为固定值。同时,考虑到车速v与输出转速ωc之间存在固定比例关系,因此车速跟踪控制可等效为转速跟踪控制。

综上,以响应时间和跟踪精度作为性能指标,设定三步法控制要求为:1)速度响应时间<0.2s;2)跟踪误差<0.1m/s。

2.2 控制器模型

(15)

选取系统状态方程为:

(16)

(17)

定义可测变量和系统矩阵分别为p和Bp,系统状态矩阵为:

(18)

三步法构建车速跟踪策略具有较强的实时性、规范性和简洁性[9]。分三步构建三步法控制器:1)构建类稳态控制律,提高系统控制响应时间;2)引入参考动态前馈控制律,综合考虑多项误差以补偿控制器;3)引入跟踪误差,在目标车速与跟踪车速中加入基于误差进行系统反馈,提高系统鲁棒性。设计思路和整体控制如图2所示。

图2 低速巡航车速跟踪控制原理

a)类稳态控制

(19)

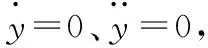
(20)

b)参考动态前馈控制

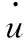
(21)

(22)

(23)

结合类稳态控制律fs(x)=0,可得前馈控制

(24)

c)误差反馈控制

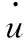
(25)

则

(26)

在系统加入跟踪误差反馈

e1=y*-y

(27)

可得跟踪误差动态方程

(28)

(29)

(30)

求导V1:

(31)

(32)

如果k1>0,k2>0,拉普拉斯变换误差方程后会渐进稳定:

s2+k1s+k0=0

(33)

(34)

(35)

则新Lyapunov函数

(36)

可得

(37)

定义

(38)

整理得

(39)

(40)

d)系统总控制律

整理上述控制律可得

(41)

定义控制参数:

(42)

利用三步法构建AMT低速巡航总体控制律:

(43)

2.3 实现控制律

(44)

图3 二阶输入整形滤波

2.4 鲁棒性验证

考虑到系统的多项扰动因素,采用总扰动d描述所有的信号扰动、误差及系统不确定因素,d的系数因子为Г,则

u=uim+Γd

(45)

前文误差转化为:

(46)

(47)

Lyapunov函数转化为

(48)

(49)

对于鲁棒性的调整来说,k1和k2分别影响了e1和e3的衰减速度。要想提高性能,则需要尽量提高二者数值,但会带来控制器的高增益,反而适得其反[12]。

3 控制策略试验分析

3.1 试验环境及改装

本研究试验车辆为奔腾MT-B50(图4)。由于该车为MT车型,为验证三步法对AMT低速巡航的车速跟踪性能,本文需要对车辆进行改造。由于电控液动式离合器位移执行机构具有过载强、容量大、速度快和精度高等优点,采用电控液动式精确捕捉并控制离合器的位移(图5)。在发动机上固定电控离合器机械部分,采用两进一出的三通阀连接踏板和电控离合器,并将出口连接液压管路,此时踏板不起作用,只由执行机构进行自动控制,最终结果如图6所示。

图4 试验用车(奔腾MT-B50)

图5 电控离合器执行机构

图6 执行机构

常规车辆的车速信号由无源轮速传感器获取,信号微弱且处理困难,并且低速巡航时的测量精度很低,无法适应实验条件。因此,换上图7所示的高稳定、低成本和简易的霍尔轮速传感器。

图7 霍尔式传感器

3.2 三步法控制结果分析

对车辆从静止启动加速后,车速出现阶跃变化时的三步法控制试验结果进行分析,结果如图8所示(本刊为黑白印刷,如有疑问请咨询作者)。分析图8(a)和图8(b)可知,试验车辆从静止启动至巡航车速过程与目标车速贴合较好,响应速度快、延迟效果小,整个跟踪过程无明显超调,具有良好的稳定性和准确性;同时,试验车辆在静止启动和稳定跟踪状态下的跟踪误差分别为0.094m/s和0.052m/s,实验结果满足控制要求。分析图8(c)和图8(d)可知,与实际情况相符,离合器的转矩与位移在整体上表现出对称关系,离合器的接合程度随着转矩变大而更深,且位移值越小。分析图8(e)可知,除车辆加速过程,低速巡航下的发动机转速与离合器转速呈正相关,且前者始终大于后者,此时离合器处于滑摩状态。

图8 实车试验结果(阶跃变速)

对车辆从静止启动加速后,车速出现正弦变化时的三步法控制试验结果进行分析,结果如图9所示。分析图9(a)和图9(b)可知,试验车辆从静止启动至巡航车速过程与目标车速贴合较好,响应速度快、延迟效果小,整个跟踪过程无明显超调,具有良好的稳定性和准确性;同时,试验车辆在静止启动和稳定跟踪状态下的跟踪误差分别为0.094m/s和0.052m/s,实验结果满足控制要求。分析图9(c)和图9(d)可知,低速巡航中的车辆不需要较大的驱动力矩,因此离合器传递转矩也不会很大。分析图9(e)可知,与阶跃变速情况相似,离合器处于滑摩状态。值得一提的是,离合器转速从20s开始直至24s出现明显上升,而发动机转速出现下降,这是负载转矩随期望车速上升而增大造成的正常现象。综上,静止启动及稳定跟踪过程中的车速始终变化平稳,误差较小,无论是体验感还是控制要求均符合预期。

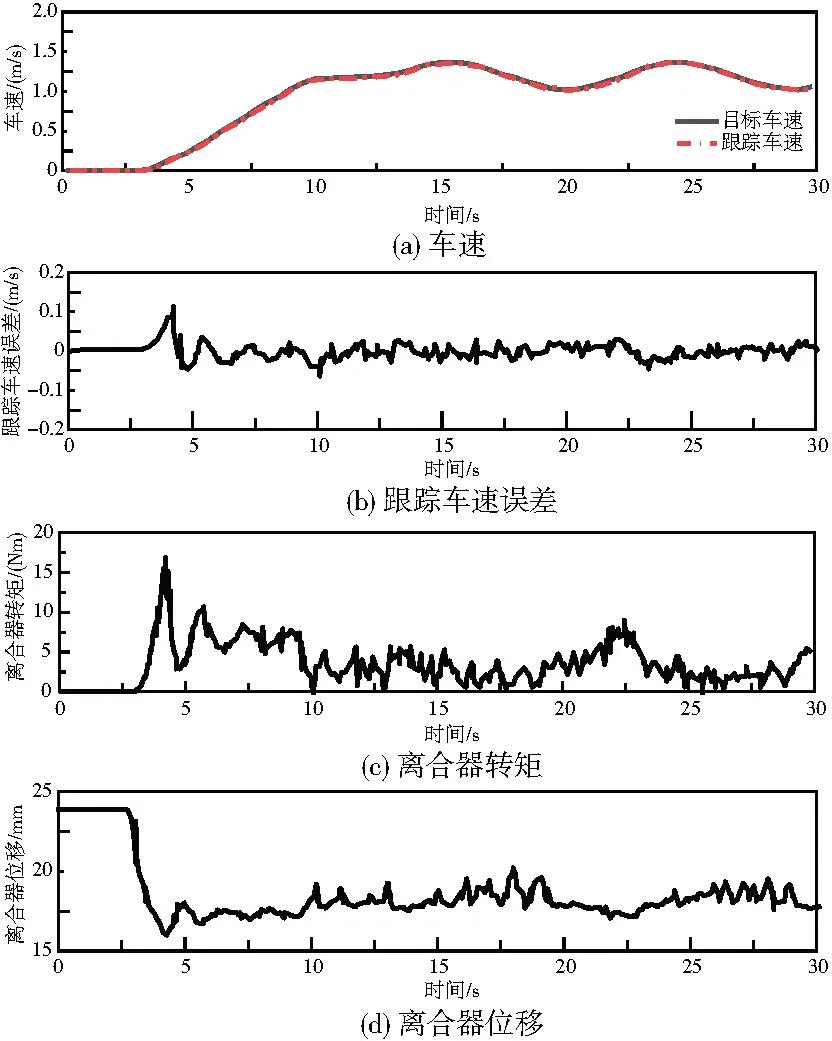
图9 实车试验结果(正弦变速)

3.3 控制方法对比

对比分析PID与三步法在阶跃车速变化中的试验结果,如图10所示。对比PID控制结果,三步法控制结果具有更好的试验结果,超调量可忽略不计,响应时间较短,几乎不存在延迟效果,并且在精度上,三步法在静止启动时的误差远小于PID法(0.094m/s <0.177m/s),稳定跟踪时的误差同样满足控制要求(0.036m/s<0.100m/s)。

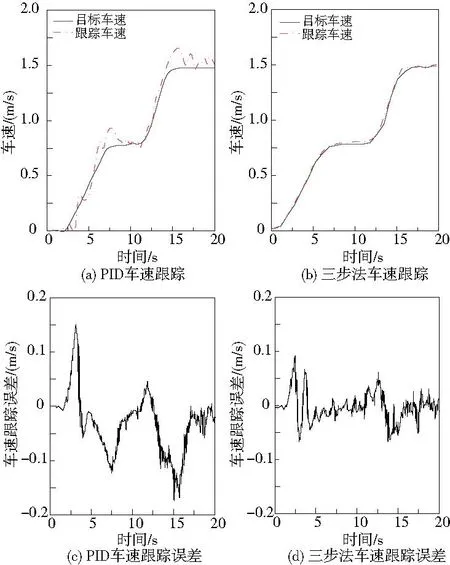
图10 PID与三步法试验结果对比(阶跃变速)

对比分析PID与三步法在正弦车速变化中的试验结果,如图11所示。对比PID控制结果,三步法控制策略无论是静止启动还是稳定跟踪,都具有更好的试验结果,超调量可忽略不计,响应时间较短,几乎不存在延迟效果。三步法在静止启动时的误差远小于PID法(0.073m/s <0.134m/s),稳定跟踪时的误差同样满足控制要求(0.038m/s<0.100m/s)。

图11 PID与三步法试验结果对比(正弦变速)

结合上述内容,对PID法和三步法的控制结果对比分析可知,本文构建的三步法控制器对于低速巡航中的AMT车辆,整体上具有更加优异的跟踪效果和控制效果,响应时间更短,跟踪误差更小,延迟效果最低,满足本研究的控制要求。

3.4 鲁棒性试验

本文进一步在平道和坡道上对三步法控制策略进行鲁棒性试验,以验证适用性和稳定性。

图12为搭载三步法控制策略的试验车辆在平道上的随机变速试验结果。分析图12(a)、图12(b)可知,跟踪车速的响应速度很快,静止启动和稳定跟踪的误差分别为0.097m/s和0.067m/s。分析图12(c)、图12(d)可知,计算值与目标值的整体变化趋势相似,由于试验车辆处于低速巡航过程,离合器传递转矩和位移并未出现大幅波动,提高了车辆稳定性和司机驾驶舒适性。分析图12(e)可知,静止启动加速中的离合器转速不断增大且逐渐趋于发动机转速,离合器处于滑摩状态。

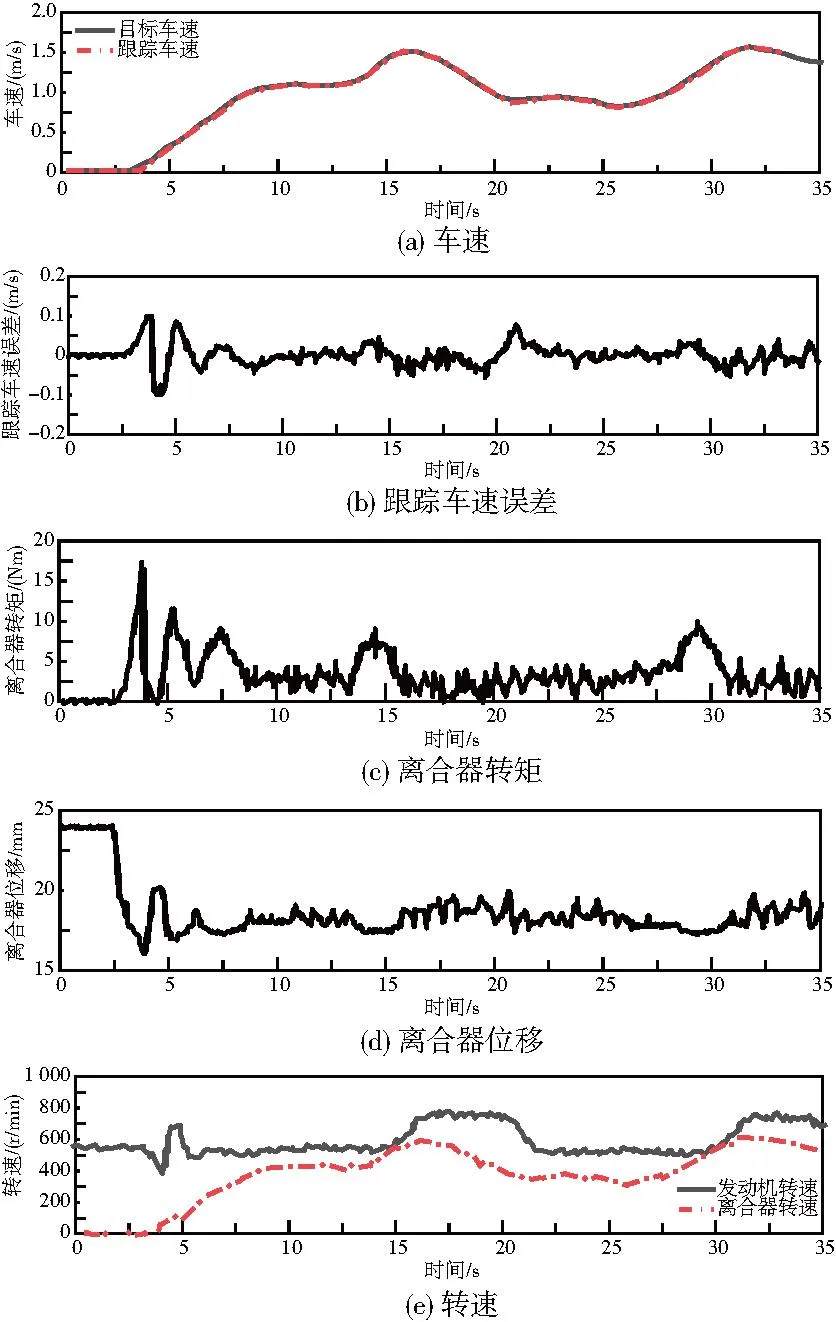
图12 三步法实车试验结果(平道随机变速)

图13为搭载三步法控制策略的试验车辆在坡道上的随机变速试验结果。分析图13(a)、图13(b)可知,相比于平道行驶,坡道行驶中跟踪误差出现略微增大,但整体仍满足控制要求,静止启动和稳定跟踪误差分别为0.098m/s和0.071m/s。分析图13(c)、图13(d)可知,试验车辆在坡道受阻,跟踪车速相同时需要提供更大的驱动力矩和传递力矩,所以离合器的传递转矩比平道的更大。分析图13(e)可知,静止启动加速中的离合器转速不断增大且更快趋近于发动机转速,离合器处于滑摩状态。整体来看,无论是阶跃变速、正弦变速还是随机变速,试验车辆的控制过程平稳缓和,满足了三步法控制器有效性的同时,也保证了鲁棒性和适应性。

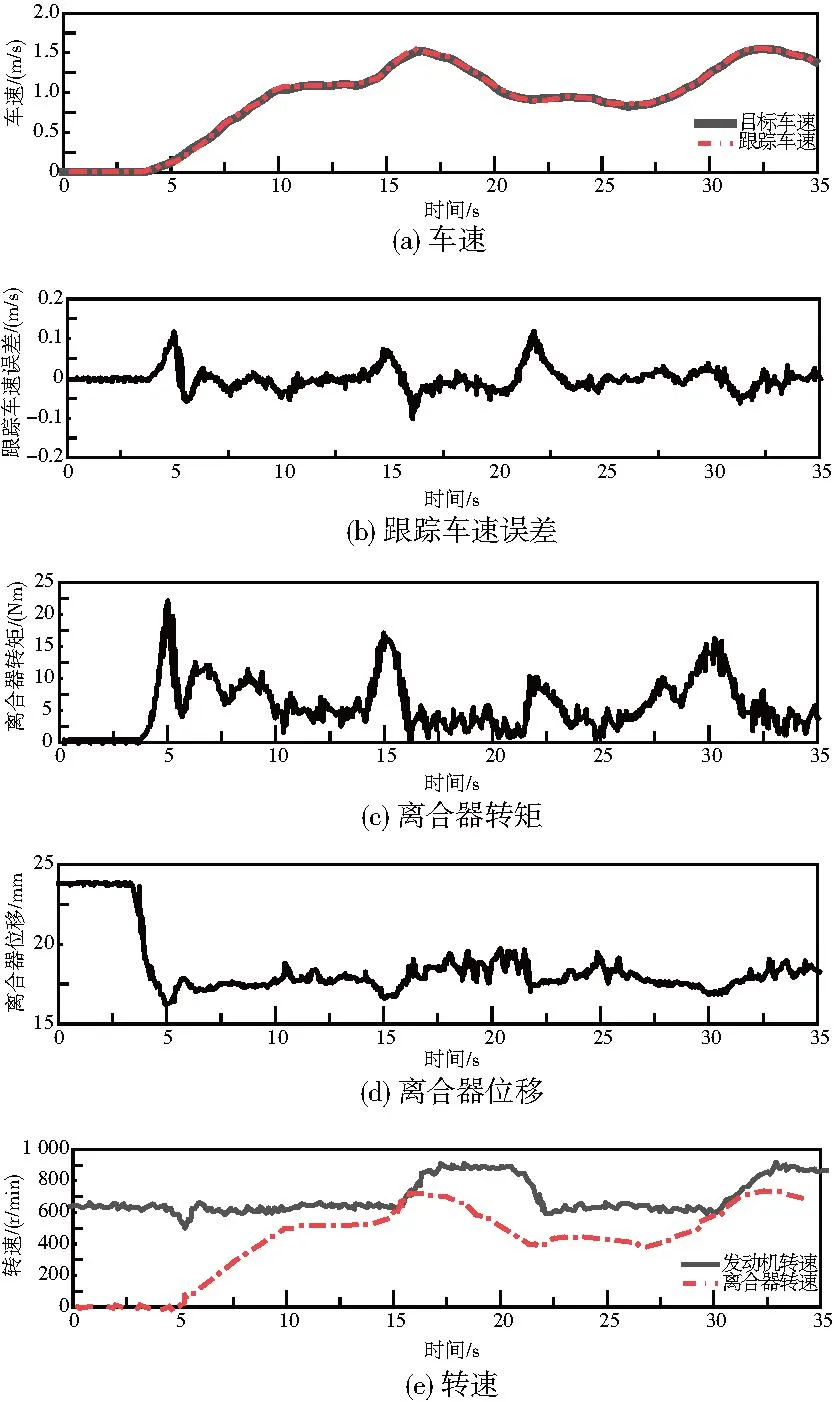
图13 三步法实车试验结果(坡道随机变速)

4 结语

本文基于AMT车辆动力传动系统中的动力学特性,构建了发动机、离合器和整车运动的数学模型;简化了AMT传动系统,提出了低速巡航中的离合器控制要求,通过Lyapunov函数对三步法控制器进行鲁棒性分析,最后通过改造车辆的实车试验对本文方法进行验证。

试验结果表明,对比PID控制法,无论是阶跃变速、正弦变速还是随机变速,无论是平道跟踪还是坡道跟踪,三步法控制策略在AMT低速巡航中均具有更优的跟踪效果和控制效果,响应时间更短,跟踪误差更小,延迟效果最低,满足本研究的控制要求。