基于有限差分法的一维电主轴热态特性分析

丁卓琛,沈沐霖,赵仕安,赵东方

(中国石油大学(华东),山东 青岛 266580)

0 引言

电主轴是数控机床的三大核心部件之一,同时也是主要热源之一[1]。数控机床的加工精度很大程度上取决于电主轴的热态特性,研究表明热误差是数控机床的最大误差源,占总误差的 40%～70%[2]。因此,电主轴热态特性分析对减缓精度损失具有重要意义,相关研究具有较高的科研与工程价值。

热态特性是指系统的热力学参数,包含温度、热变形、热应力等,本文的研究对象为电主轴轴向温度场分布。为了获取其一维特性,需要对三维模型进行一维化。一维化的核心在于把截面的相关参数等效到一个节点处,形成一个沿轴向线性分布的点集,通过研究各节点之间的热传递从而推导出一维主轴轴向的温度分布。目前,对于一维温度场的研究方法主要分为解析法和数值法,其中数值法主要包括有限差分法、有限元法、神经网络法。

目前,国内很多学者都对电主轴热态特性进行了分析与研究,有其独到之处,但也存在一些不足。天津大学的姜杉等[3]在不考虑主轴与周围空气热交换的情况下对传热方程进行简化,将非齐次偏微分方程转化为齐次形式进行求解,但简化本身存在一定误差,同时对边界条件提出了更高要求。西安交通大学的颜宗卓等[4]将热源测点温度变化量与响应函数进行卷积积分来估算电主轴系统的温度分布,模型的精度与实验数据的数量和准确性有关,对硬件条件要求高。哈尔滨理工大学的李宝伟[5]基于RNN神经网络建立了电主轴热特性模型,训练样本对神经网络的质量起决定性作用,为获取精确模型往往需要大量数据支撑;尹相茗[6]将简化后的电主轴模型导入Workbench进行了稳态热分析,结果较为精确但建模过程复杂。兰州理工大学的王志强[7]利用Mechanical APDL对于电主轴的稳态和瞬态温度场进行研究,通过二维单元对三维模型进行简化,但步骤仍过于繁琐。

对于温度场的研究,科研和工程实践中广泛应用ANSYS Mechanical APDL和Workbench 作为分析工具,但是针对于一维问题在某些方面仍存在不足。具体来说:Mechanical APDL中没有针对于一维梁单元设置热力分析单元,为了进行相关分析,可采用一维杆单元Link 33、Link 34替代,但不能考虑截面形状、面积以及材料的比热容,经检验结果存在偏差。Workbench通过将三维模型划分为若干单元体进行分析,其仿真精度高,但需对结构进行建模,获取一维特性的经济、时间成本较高。

有限差分法通过迭代进行运算,与有限元法相比计算速度快,对计算机性能要求低,与神经网络法相比步骤简单、适应性强。本文从理论分析出发,借助传热学相关理论,对主轴进行一维化处理与结构划分,建立了一维主轴温度场模型,基于有限差分法实现数值计算。计算过程中仅涉及代数方程求解,运算速度快,对于不同的电主轴仅需更改相关参数设置,实现了对于一维电主轴温度场的快速、适用性强的计算分析,可为电主轴设计和工程应用提供参考。

1 热源分析及计算

电主轴内部有两大热源:内部电机和两端轴承。为了获得主轴温度分布规律,需要对热源产热量进行计算,从而获得内部热源的发热率。

本文研究对象为额定功率30kW的电主轴在其额定转速9 900r/min下的温度分布情况。

1.1 内部电机生热

电主轴内部普遍采用三相交流电动机,电机产生的热量可以从功率或能量损耗的角度分析,理论上认为输入功率全部转化为驱动电主轴运转的能量,但是实际上存在机械损耗、磁损耗、电损耗和附加损耗,故电机是存在一定机械效率的。

电动机输入功率为

(1)

取电机效率η为90%,电机损耗为

Pw=(1-η)P

(2)

电主轴以额定功率运行时,可以由上式计算出各个部分的损耗,并假设损耗全部转化为热量,因此电机各部分的生热率可由下式计算:

(3)

式中:Qi为各部分的热功率,W/m3;V为热源的体积,m3。

对于本文研究的一维化模型,需将截面的相关参数等效到一个节点处,根据各部分面积在总面积中占比对生热率做加权,可得电机部分的生热率

(4)

式中:Si为各部分所占面积,m2;S为总面积,m2。

1.2 前后轴承生热

摩擦是轴承运转中最主要的热源,具体包括滚动体与外圈、滚动体与内圈以及保持架和润滑剂的摩擦[8]。根据经验公式[9],由摩擦产生的热量Qf可表达为

(5)

式中:M为摩擦力矩,N·mm;n为转速,r/min。

根据经验公式,轴承摩擦力矩M与速度无关,主要由两部分组成:一是润滑剂自身黏度引起的摩擦力矩M0,二是在载荷作用下的摩擦力矩M1,具体如下式[9]:

M=M0+M1

(6)

工程中常用润滑剂的运动黏度ν普遍满足ν·n≥2 000,因此黏性摩擦力矩M0可表达为

(7)

式中:Dm为轴承平均直径,mm;f0为与轴承类型和润滑方式有关的系数,对于单列角接触球轴承取f0=2。

轴承载荷力矩M1满足

M1=f1P1Dm

(8)

式中:f1是与轴承类型、额定载荷及当量静载荷有关的系数;P1为轴承承受载荷,N,计算方法如下:

f1=0.001 3(P0/C0)0.33

(9)

P1=Fa-0.1Fr

(10)

式中:P0为当量静载荷,N;C0为基本额定静载荷,N;Fa为轴向载荷,N;Fr为径向载荷,N。

2 主轴热态特性模型建立

2.1 传热学理论基础

传热学中定义的传热方式有3种:热传导、热对流和热辐射,传热过程由这3个环节串联而成的。本文主要研究稳定运行阶段电主轴的温度场分布,因此,将电主轴与周围环境的热交换近似看作稳态导热过程,因辐射换热量较少可以忽略不计。

2.2 一维传热公式

对于主轴内各微元体来说,满足能量守恒方程:

dΦin+dQ=dΦout+dU+dΦs

(11)

式中:dΦin为导入总热流量,W;dQ为内热源的生成热,W;dΦout为导出总热流量,W;dU为热力学能增量,W;dΦs为对流换热量,W。图1为微元体热态特性。

图1 微元体热态特性

由傅里叶定律,导入、导出微元体的热流量分别可以表示为:

dΦin=Aqx=-λAc∂t/∂x

(12)

dΦout=Aqx+dx

(13)

式中:λ为材料的热导率,W/m3;Ac为截面面积,m2;t为温度,℃,与坐标x和时间τ有关。

在所研究的范围内,热流密度函数q是连续的,可以展开为泰勒级数的形式:

(14)

式中dx为无穷小量,可近似地取级数前两项,即

(15)

微元体的热力学能增量可以表示为

(16)

式中:ρ为材料密度,kg/m3;c为材料的比热容,J/(kg·K)。

微元体的生热量可以表示为

(17)

由牛顿冷却公式,热对流交换热量为

dΦs=PhdxΔt

(18)

式中:P为截面周长,m;h为传热系数,W/(m2·K)。

将上述相关推导代入式(11),可得一维主轴传热公式

(19)

2.3 主轴划分

对于一维电主轴来说,由于生热率、传热系数等参数的不同,各部分呈现出不同的温度分布规律。本文根据热力学特性,将电主轴划分为电机部分、轴承部分、主轴部分,如图2所示。

图2 主轴划分图

电机部分、轴承部分是电主轴内部两大热源,在建立模型时将这两部分按照微元体内热源的方式进行定义、计算。电主轴各个部分与外界的热传导方式不同,传热系数也各不相同。电机部分主要通过冷却水道中的冷却水带走内部产生的热量,其传热系数与冷却水道的截面积、长度、冷却水流量等参数有关。轴承中广泛应用油气润滑技术,通过内部压缩空气散热,其传热系数与压缩空气的平均速度有关。主轴部分直接与空气进行对流换热,其换热系数与主轴表面转速有关。

经计算,相关参数设置如表1所示。

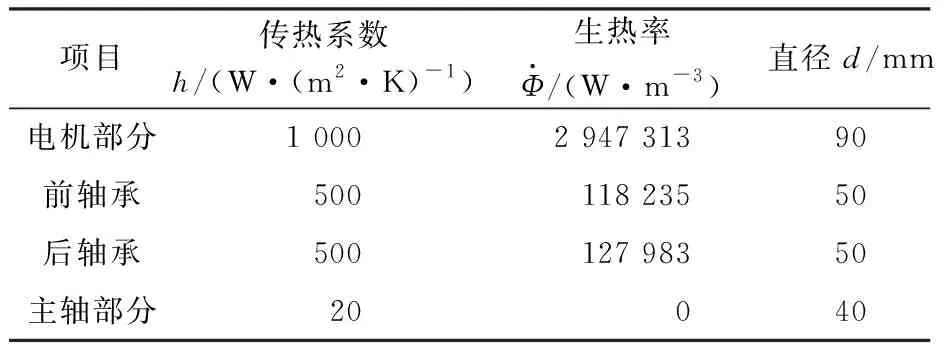
表1 系统参数设置

2.4 一维温度场建模与数值模拟

对主轴进行离散化处理,将主轴划分为282个节点,首尾两节点温度与室温一致作为边界条件,如图3所示。

图3 一维电主轴离散化示意图

为了获得针对单一变量轴向位置的差分格式,将温度对位移的导数转化为差商形式如下:

(20)

将上文推导的一维传热方程进行离散化,相邻节点间表达式如下:

(21)

将差分格式进行整理可得系统方程如下:

(22)

将系统方程通过欧拉法求解:

Tn+1=Tn+F(τn,xn)(τn+1-τn)

(23)

式中:τn代表第n个时间步;F(τn,xn)是主轴各节点在τn时刻导数的矩阵。

在MATLAB中完成上述程序编写,可以实现一维主轴轴向温度的快速获取,运行结果如图4所示。

图4 一维主轴温度场分布情况

由图4可以看出,温度最高的部分是电机中部,为78℃,电机内部发热对于主轴温升影响最大。轴承对于温升的影响不是很明显,由于前后轴承类型不同,温升情况也不同,分别呈现出36℃、37℃的温度。

3 有限元模拟验证

本文采用一维化的方式对电主轴温度场进行分析,用截面的综合属性来描述每一截面,由于结构限制,导致采用实验法获得电主轴内部温度比较困难,实验验证可行性差。而采用ANSYS Workbench进行有限元分析是行业内对结构进行热分析最常用的方式,可以全面地获取电主轴内部的温度数据,同时其结果具有一定准确度与可靠性。因此本文采用Workbench进行有限元仿真的方式来验证本模型。

验证的主要思路为沿主轴径向取等距平行于轴线的路径,将这些路径上温度的平均值作为电主轴一维温度场的仿真结果与模型计算结果对比,具体步骤如下。

1)根据热分析需要,在三维建模过程中对模型适当简化,在Solidworks中完成建模,如图5所示。

图5 Solidworks三维模型

2)将建立好的模型导入ANSYS Workbench稳态热分析模块中,在Engineering data模块中设置材料参数,在Mesh模块中实现网格划分。

3)将上文计算好的相关参数通过Environment模块加载到电主轴模型上,包括初始温度、换热系数、生热率等。

4)根据上文结构划分,沿轴向等距建立一系列平行于轴线的路径(path),如图6所示。

图6 温度测量路径

5)结果中查看路径轴向方向温度数据,如图7所示。

图7 Workbench仿真结果

6)将相关数据导入MATLAB取均值后绘图,并与本文建模所得曲线比较(图8)。

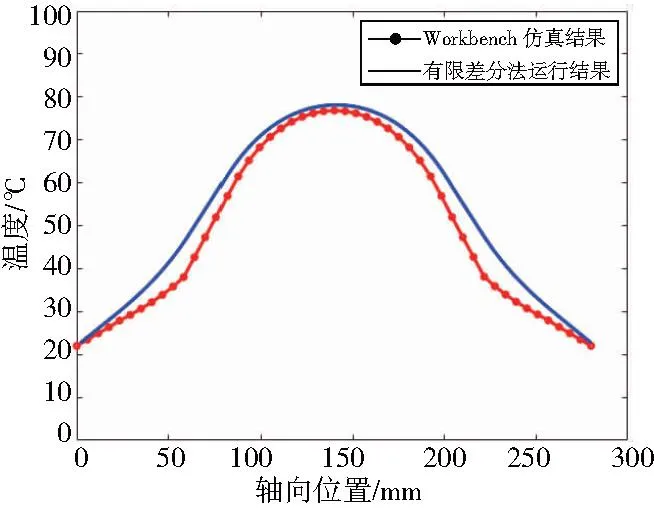
图8 建模结果和仿真结果比较

由图8可以看出,本文提出模型的计算结果与仿真结果基本一致,误差维持在7℃以内,高温区域两曲线基本重合,可以满足工程实际使用要求。

4 结语

本文主要研究了电主轴的一维温度场分布,对电主轴模型进行了一维化处理,结合热力学特性对模型进行合理的结构划分,基于传热学理论建立了电主轴一维传热模型,通过有限差分法获得数值解,与有限元仿真结果呈现较高一致性,为电主轴的结构设计和工程应用提供一定参考。本方法的特点在于简化了一维温度场求解步骤,将非齐次偏微分方程转化为代数方程组进行计算,大大提高了计算速度。针对不同实际情况仅需调整参数,不需重新进行建模,计算时间相较于其他方法大大减少。

本文所建立模型与仿真结果存在一定差异,主要原因是对一维问题的研究存在局限性,但其对于多维传热以及复杂结构的热特性分析仍有参考意义。