三叉杆滑移式万向联轴器油膜刚度的分析

房玉良,赵海霞,付善昭,韩相锋,彭智杰

(青岛科技大学 机电工程学院,山东 青岛 266061)

0 引言

三叉杆式万向联轴器主要应用于汽车的传动系统,通常水平安装在汽车驱动桥与变速器之间,实现驱动桥与变速器之间的运动与转矩的传递,同时能够提供角向补偿能力,其属于准等角速万向联轴器[1]。近年来国内外学者大多都是对三叉杆式万向联轴器的运动学、动力学以及摩擦润滑方面的研究,对三叉杆式万向联轴器油膜刚度方面的研究很少。万向联轴器作为汽车传动系统中必不可少的关键零部件,对其低振动、低噪声的性能要求越来越高,万向联轴器的振动使摩擦磨损加剧,降低疲劳寿命及转矩和运动传递的稳定性,而联轴器的油膜刚度作为内激励之一,对其振动性能有很大的影响,当联轴器几何参数发生变化时,油膜会发生变形,油膜刚度也会随之改变。因此研究联轴器几何参数对油膜刚度的影响规律,对实现联轴器的减振降噪,具有重要的意义。QIN等[2]通过接触体的卷吸速度、负载以及曲率求解得到油膜刚度,并分析各参数对油膜刚度的影响。ZHANG等[3]提出线接触弹流润滑振动模型,研究卷吸速度、粗糙表面形貌对油膜刚度的影响。WU等[4]分析Jeffcott轴承转子系统临界转速时计入了油膜刚度和油膜阻尼。杨静等[5]通过实验建立了油膜刚度测量模型,分析了径向载荷与油膜刚度的关系。

本文基于表面粗糙度理论和弹流润滑理论,建立了三叉杆滑移式万向联轴器弹流润滑油膜刚度计算模型,研究分析卷吸速度、表面粗糙度等的规律。

1 三叉杆滑移式万向联轴器模型

1.1 滑移销与主动轴孔的接触模型

三叉杆滑移式万向联轴器的结构如图1所示。其由主动轴、滑移销、关节轴承、三叉杆、从动轴五部分组成,主动轴孔与滑移销的配合接触面是主要的受力面。为了能够形成流体动压润滑,在滑移销上增加了一组圆环,结构如图2所示,使主动轴孔与滑移销之间的接触区域,变成了几个局部先收敛、后发散的接触区,本文主要对滑移销与主动轴孔接触面间的油膜刚度进行分析。

1—主动轴;2—滑移销;3—关节轴承;4—三叉杆;5—从动轴。图1 三叉杆滑移式万向联轴器结构图

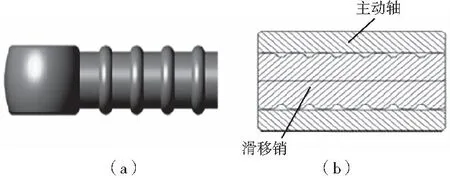
图2 有圆环结构的滑移销及配合剖视图

1.2 运动学模型

当主动轴与从动轴成一定角度时,滑移销在主动轴孔中往复滑移,完成转矩的传递,图3为三叉杆万向联轴器的简化几何模型。

图3 三叉杆滑移式万向联轴器简化几何模型

根据图3,滑移销相对于主动轴孔的滑移方程[6]为

(1)

式中:R为滑移销回转半径,mm;φ为主动轴转过的角度;β为主动轴与从动轴之间的夹角。

对式(1)两端分别求导,得到滑移销的速度方程

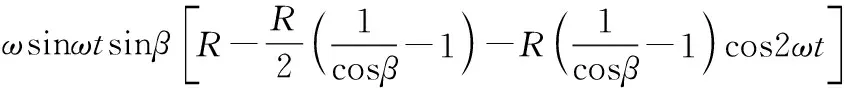
(2)

式中ω为输入轴角速度,rad/min。

根据文献[6],三叉杆滑移式万向联轴器的流体动压润滑可以看成线接触弹流润滑问题,将主动轴孔与滑移销的接触看作一个无限长圆柱和一个平面之间接触的问题,其几何简化模型如图4所示。假设圆柱b静止不动,即ub=0,平面a的速度即为滑移销在主动轴孔中往复滑移的速度,滑移销相对于主动轴孔的速度可简化为

图4 线接触几何模型图

ua=Aωsinωt=A·2πf·sin(2πf·t)

(3)

式中:A为振幅,mm;ω=2πf;f为滑移销往复滑移频率,且滑移销往复滑移频率与主动轴转动频率相等,Hz;t为时间,s。

2 油膜刚度计算模型

2.1 表面粗糙形貌

由于加工工艺、零件材料等不同,很难加工出绝对光滑的零件表面。表面粗糙形貌由许多微型凸峰和凹谷组成,假设其接触区域为单粗糙峰,即只考虑滑移销有表面粗糙度,主动轴孔为光滑平面,滑移销与主动轴孔的表面粗糙度模型如图5所示。x为滑移销滑移速度方向,z为油膜厚度方向,滑移销与主动轴孔之间通过润滑油,其粗糙表面形貌可以由多个正弦信号叠加解析,表面粗糙度函数为

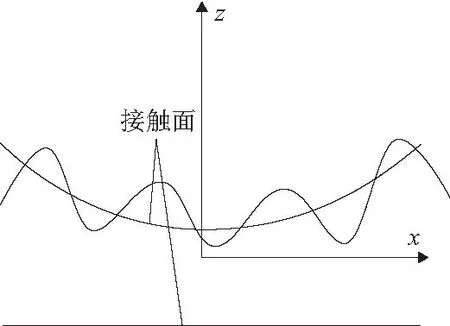
图5 表面粗糙度模型

(4)

式中:x*区间为[-1,+1];Af为滑移销表面粗糙度的幅值;lf为滑移销表面粗糙度波长;t为时间。

2.2 基本方程

一般线接触牛顿流体的Reynolds方程[7]为

(5)

式中:x为卷吸速度方向标量;ρ为润滑油密度,kg/m3;p为油膜压力,Pa;h为油膜厚度,m;η为润滑油动力黏度,kg/m3;us为卷吸速度,m/s,us=(ua+ub)/2,ua=Aωsinωt,ub=0。

方程(5)的边界条件为

P(x0,t)=0,p(x1,t)=0,p≥0(x0≤x≤x1)

式中x0和x1为计算域的边界坐标。

粗糙表面的膜厚方程为

(6)

式中:h0为中心膜厚,mm;R为等效曲率半径,mm;e(x)为变形方程。

(7)

式中:p(s′)为压力分布函数;E′为两接触面的综合弹性模量,Pa;s′为压力p(s′)到原点的距离。

设主动轴孔表面和滑移销表面的弹性模量分别为E1、E2,其Poisson比为v1、v2,则

(8)

黏度-压力关系式为

η=exp{(lnη0+9.67)[(1+5.1×10-9p)z-1]}

(9)

式中:η为润滑油黏度;η0为p=0时润滑油的黏度;z=α/[5.1×10-9(lnη0+9.67)],α为黏压系数。

密度-压力关系式为

ρ=ρ0[1+(0.6+10-9p)/(1+1.7×10-9p)]

(10)

式中ρ0为零压时润滑油密度,kg/m3。

载荷平衡方程为[8]

(11)

式中W为实际载荷,N。

2.3 油膜刚度计算方程

根据刚度的定义,可知

(12)

式中:kfilm为两表面间油膜刚度;ΔW为接触面的分布载荷;δ为接触面间油膜压缩变形量。

2.4 方程无量纲化

式中:pH为Hretz线接触压力;b为Hretz接触区半宽。

联立式(4)-式(12),通过Newton-Raphson迭代法进行计算。由于润滑油膜的初始形状比较粗糙,理想状态表面的压力解与实际情况的压力值存在较大的差距,导致求解的结果不容易收敛,进而通过逐渐增加表面粗糙度幅值的方法来求解较大的表面粗糙度值,当表面粗糙度逐次递增后,新的起始值就是通过前一次的迭代计算并进行修正后得到的。随着压力的变化,润滑油膜的厚度和黏度也会随之发生变化,所以,首先应该设置起始压力值,即Hertz线接触压力值,从而得出初始的润滑油膜厚度和黏度,对上述迭代进行重复计算,当相邻两次迭代计算的压力差值符合收敛标准时,结束迭代计算,最终得出满足要求的膜厚与压力值。周期性收敛准则[9]为

(13)

式中“k+1”、“k”分别表示当前循环与前一次循环。当超过4个周期且满足收敛准则时,得到收敛解,结束计算。

图6为上述计算过程的流程图。

图6 数值计算流程图

3 仿真结果及分析

三叉杆滑移式万向联轴器的主动轴与滑移销的材料均为40Cr,其材料属性如表1所示。各参数初始值为:x1=-x0=(-4.5b) m,载荷W=60kN/m,表面粗糙度幅值Af=0.01,波长lf=0.5。主动轴孔半径为10mm,滑移销半径为9.95mm,联轴器回转半径为30mm,主动轴与从动轴夹角β为10°,对应的振幅A=5.129 1mm,假设轮胎直径为0.59m,由文献[10]可知联轴器的转动频率等于轮胎实际的转动频率,取车速分别为50km/h、100km/h、150km/h、200km/h,则对应联轴器转动频率为7.5Hz,15Hz,22.5Hz,30Hz,滑移销对应最大滑移速度分别为248mm/s、487mm/s、725mm/s、966mm/s,则油膜卷吸速度(滑移销与主动轴孔接触面的平均速度)分别为124mm/s、243.5mm/s、362.5mm/s、483mm/s;润滑剂选择MP-3,在温度313K下,η0=0.1Pa·s,α=23.5GPa-1,ρ0=890kg/m3。

表1 主要零件的材料属性

3.1 载荷、润滑油黏度及卷吸速度对油膜刚度的影响

图7为载荷、卷吸速度、黏度对油膜刚度的影响。由图7(a)可以看出,油膜刚度随着载荷的增加而增大,此结果与文献[11] 研究规律一致。这是因为载荷的增大导致油膜厚度的减小,使滑移销与主动轴孔的距离越小,油膜越来越难被压缩,最终导致油膜刚度变大。在远离接触区中心的位置,油膜刚度的变换幅度较小,在接触区中心位置变换幅度最大,且油膜刚度在峰值处的变化最为明显。从图7(b)可知,随着润滑油卷吸速度的增大,油膜刚度减小,油膜刚度的最大振荡幅度在中心位置左侧。由于卷吸速度的增加导致了油膜厚度的增加,而润滑油膜厚度的增加使油膜刚度减小。图7(c)中,当其他条件不变时,润滑油黏度的增加导致油膜刚度有所增大,润滑油黏度的增加必然导致油膜厚度随之增加,较大的油膜厚度反而会使油膜刚度减小。通过观察可知,润滑油黏度对油膜刚度的影响比卷吸速度、载荷对油膜刚度的影响小(本刊为黑白印刷,如有疑问请咨询作者)。

图7 载荷、卷吸速度、黏度对油膜刚度的影响

3.2 表面粗糙形貌对油膜刚度的影响

图8为不同表面粗糙度幅值对油膜刚度影响。通过观察可知,随着表面粗糙度幅值的增大,油膜刚度呈非线性变化。这是因为膜厚随着表面粗糙度的变化呈非线性变化,而膜厚的非线性变化导致了油膜刚度无序的变化,并且油膜刚度的峰值出现在接触区中心附近。这是因为当考虑表面粗糙度时,压力及膜厚主要在接触区中心波动,同时随着表面粗糙度幅值的增加,油膜刚度的第二峰逐渐消失,油膜刚度的振荡频率也有所减小,此变化规律与文献[11]基本一致,不同之处在于油膜刚度的变化范围相对较小,这是因为本文中所研究的联轴器有利于形成动压润滑油膜的圆环,表面粗糙度对膜厚和压力的影响相对较小。图9为幅值Af=0.02 μm时不同表面粗糙度波长对油膜刚度影响。从图中可以看出,随着波长的改变,油膜刚度也呈非线性变化,油膜刚度的变化频率及变化幅度同样随表面粗糙度波长的增加而有所减小,这是因为随着波长的增大,油膜厚度的变化频率和幅度明显减小。当lf=0.05μm时油膜刚度变化较明显。通过以上分析不难发现,合适范围内的表面粗糙度幅值和波长能够有效减小油膜刚度的变化频率及幅度,提高油膜刚度性能,减弱联轴器的低频振动。

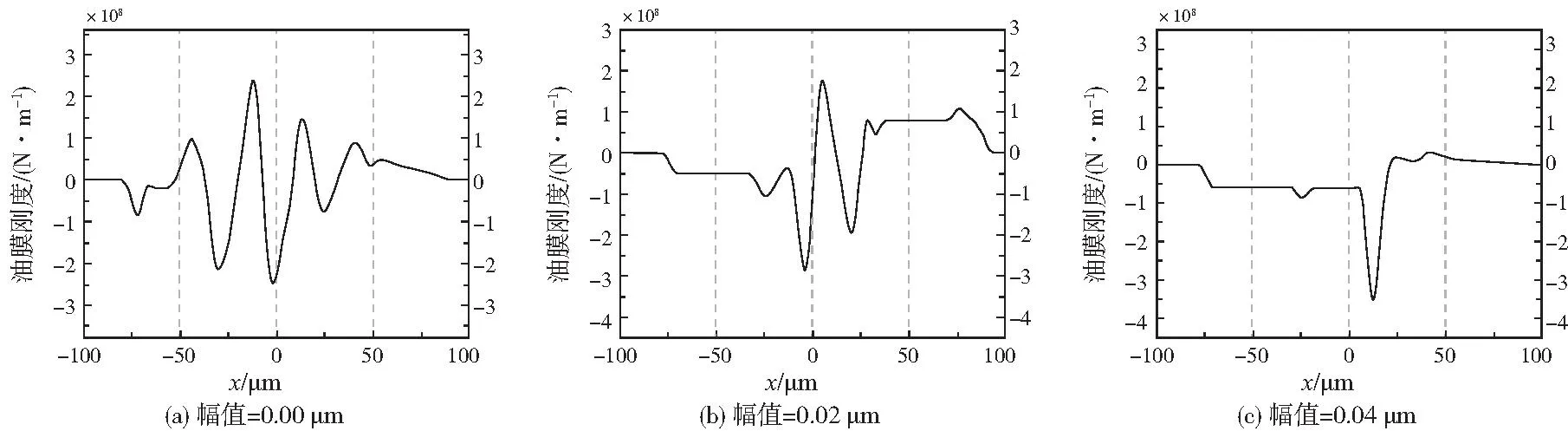
图8 表面粗糙度幅值对油膜刚度的影响

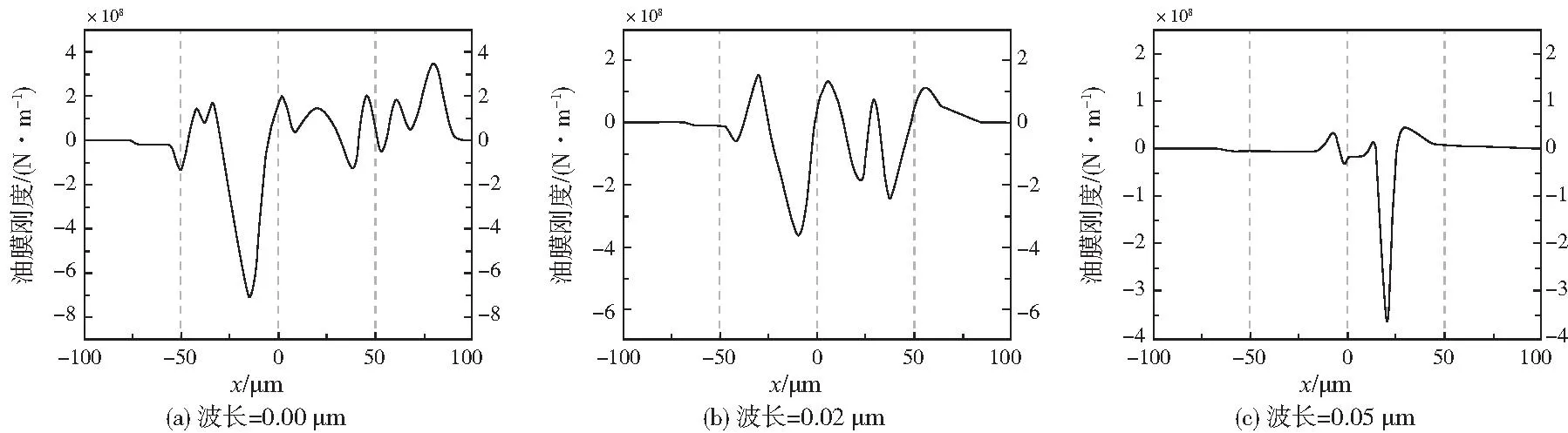
图9 表面粗糙度波长对油膜刚度的影响

4 结语

经过研究分析得知,不同的表面粗糙度、润滑油黏度及卷吸速度、接触载荷对三叉杆滑移式万向联轴器的油膜刚度有着不同的影响,具体结论如下。

1)油膜刚度随着接触载荷的增大而增大,在接触区中心位置油膜刚度变换幅度最大,油膜刚度随着卷吸速度的增大而减小,随着黏度的增加而增大,同时,相比于接触载荷及卷吸速度,润滑油黏度对油膜刚度的影响相对较小,较小的油膜刚度有利于提高接触体抵抗外力冲击的能力,从而减小振动。

2)随着表面粗糙度幅值及波长的增大,油膜刚度的变化频率及幅度变小,同时在改变幅值与波长的情况下,油膜刚度呈非线性变化,油膜刚度的最大峰值出现在接触区中心附近,由此可知一定程度的表面粗糙形貌能够提高油膜刚度性能,从而减弱联轴器的低频振动。但表面粗糙度幅值与波长又不宜过大,过大时油膜刚度发生剧变,使油膜破裂,减短联轴器的寿命。根据分析应当控制幅值在0.04μm左右,将波长控制在0.03～0.05μm之间,防止油膜破裂的同时,能够减弱联轴器的低频振动,更加稳定传递运动和转矩。