考虑腐蚀速率和不完全维护作用的管道剩余寿命预测

2024-01-03胡俊平

石油工程建设 2023年6期

胡俊平

中国石油华北油田公司第五采油厂，河北辛集 052360

管道是油气资源运输的主要方式，在国民经济发展中占有重要地位。受管输介质、大气环境和土壤条件的影响，管壁上的腐蚀缺陷随运营时间的延长不断增加[1]。据相关数据统计，我国因管道腐蚀造成的国民经济损失约占总产值的1.1%～4.5%[2-3]。研究不同检测时刻的管道剩余寿命，采用预防性的维护活动控制其退化过程，进而降低风险水平显得尤为重要。

目前，有关管道剩余寿命的预测方法大多是基于腐蚀速率或腐蚀深度数据本身进行模型构造和概率密度函数的推导[4-6]，没有考虑腐蚀速率随机性对退化趋势的影响。根据现场的采样情况，腐蚀速率往往不是随时间增大的函数，而是随机分布，且受外界因素影响较大。此外，剩余寿命的预测通常假设不同预测间隔内没有进行任何维护操作，这对于未维护或修复如旧的管道寿命预测是合理的；但实际情况下，维抢修人员会定期根据不同腐蚀程度进行诸如打磨、堆焊、补板等补强操作，增加管壁厚度，延长管道寿命。从经济性和可靠性角度出发，现场的实际维护方式多为不完全维护，管道剩余寿命随维护效果和维护次数的变化而变化，这会影响退化建模的准确性和预测精度。基于以上问题，在考虑内腐蚀速率物理模型的基础上，以残余壁厚为初始条件，对管道实施分段非线性扩散建模，用于描述其实际退化过程，采用极大似然估计法和马尔科夫链-蒙特卡洛方法进行参数估计，以期实现不完全维护状态下管道剩余寿命的准确预测。

1 模型描述

1.1 分段非线性扩散模型的建立

管道在运行过程中会经历一系列修复非新的不完全维护，通过现场监测可以获得腐蚀管道的状态数据，并与设置的预防性维护阈值进行对比，进而判断是否采取维护措施。假设腐蚀管道的不完全维护次数为i，则退化过程为i+1个阶段，当经历i次维护后壁厚达到失效阈值时需进行换管操作[7-8]，退化轨迹见图1。

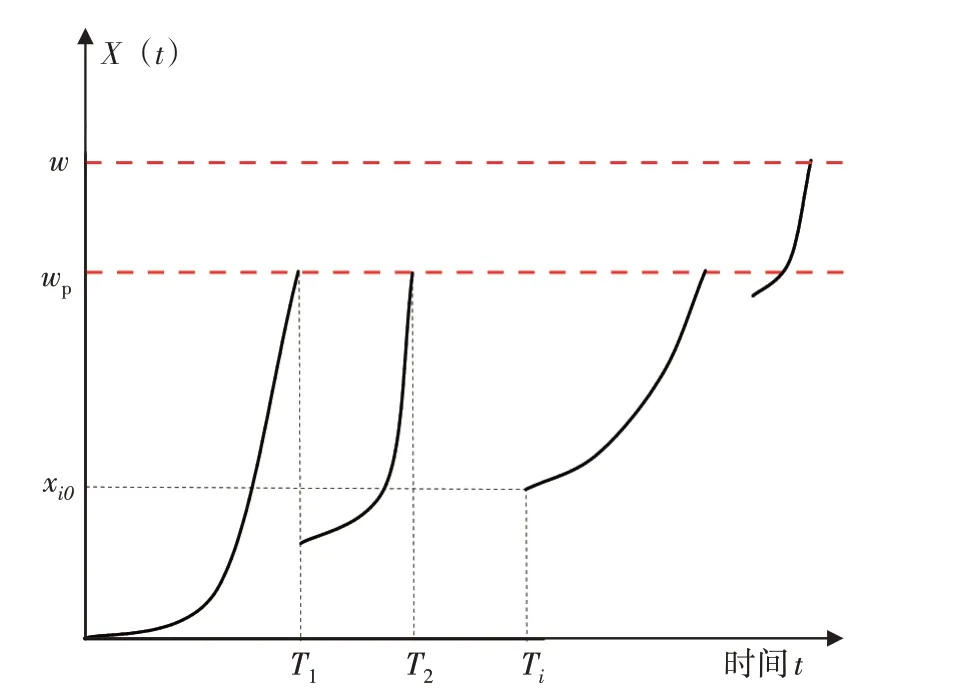
图1 不完全维护作用下的退化轨迹

鉴于腐蚀、磨损、屈曲等不可逆因素，管道每次维护的效果均不相同，残余壁厚和腐蚀速率随维护次数的增加逐渐增大，表现为非线性特性。在此，用一个非线性扩散过程表示T1～Ti阶段腐蚀深度的变化过程，故经过第i次维护后，不同阶段管道的腐蚀深度为：

式中：ηi为第i次维护后管壁残余壁厚系数，ηi～N（1-e-ai,b），其中a、b为超参数；ci为腐蚀速率变化因子；λ0为超参数；μ（τ,θ）为与时间t相关的非减函数；τ为整体变量；θ为与腐蚀相关的随机参数，即腐蚀速率；σB为扩散系数；B()为与时间相关的布朗运动。

由此可见，式（1）右边的3 个部分分别体现了不完全维护、腐蚀速率和动态变化对腐蚀深度的影响。

1.2 腐蚀速率回归模型的建立

管道在运行时易受H2S、CO2的影响，考虑到待研究管道H2S 的分压比在33～300 之间，故建立以H2S腐蚀为主的腐蚀速率模型[9]：

式中：θ1为腐蚀速率；A、B、K、C1等均为待定参数；pH2S、pCO2分别为H2S、CO2的分压。此外，腐蚀速率还与流速和温度有关，根据Nesic 等[10]、Li等[11]的研究结果，建立各自的关系式：

式中：E、C2、D均为系数，v为流速，Ea为碳钢的反应活化能，R为气体常数；T为温度。

将式（2）～式（4）合并得到腐蚀速率回归模型：

式中：A、B、K、C、D、E等均为待定参数。

2 剩余寿命概率密度函数的求解

剩余寿命可以表示为管道从检测时刻起到失效阈值的时间长度，基于首达时刻的概念，根据式（1）推导出tij时刻的剩余寿命为：

吴浈对张译称：“你又不懂业务。这个复检没价值。”防疫站出身的张译坚称自己懂业务。吴浈竟然爆粗口称：“你懂个屁！”

式中：i为tij时刻之前管道的维护次数，j为tij时刻之前管道的检测次数，Lij为tij时刻后再经过lij时间达到失效时刻的剩余寿命，xij为tij时刻的腐蚀深度。

根据本文1.1 节的假设，退化过程为n+1 个阶段，且式（6）服从逆高斯分布，则tnj时刻的剩余寿命Lnj为：

此外，两个维护时刻之间的退化量还应小于预防性维护阈值wp，则第i+1 阶段的服役时间表示为Rij，见下式：

综上所述，在考虑不完全维护作用的前提下，通过解析式（6）～式（8）得到腐蚀管道剩余寿命的概率密度函数：

3 实例分析

3.1 数据来源

某油田伴生气管道全长15.6 km，管道规格D273 mm×9.1 mm，设计输量110×104m3/d。介质中H2S 含量较高（70～150 g/m3），采用满足酸性服役条件的L245 NCS 钢，3PE 防腐层进行绝缘防护。2012 年11 月投产后，管道先后出现了不同程度的腐蚀，遂进行了不同周期的事后维护。

为了有效掌握该管道的内部腐蚀情况，在末站设置了腐蚀监测点，采用ER4015E 型远程电阻探针将腐蚀数据远传至中控室储存，见图2。此外，为保证管道清管、预膜不受影响，探针设置在管道顶端，与内壁平齐。统计2012 年11 月～2019 年8 月期间每个月的腐蚀速率和腐蚀深度共82 组数据，见图3。可见，不同时刻的腐蚀速率呈随机波动趋势，且已远超过我国腐蚀速率的控制值（0.076 mm/a）。该油田区块内其他管段均在5～7 a 内发生过穿孔泄漏。该管道分别在30 个月、48个月和65 个月进行了维护，壁厚得到有效修复，最后一次维护后该管道已无操作空间和可修补的必要，故待壁厚达到失效阈值时进行预防性更换。根据ASME B31G 的评定程序，失效阈值w按80%的壁厚（7.2 mm）设置；根据Q/SY 1180.4—2015《管道完整性管理规定第4部分：管道完整性评价》中的规定，预防性维护阈值wp按40%的壁厚（3.6 mm）设置。

图2 监测点布置

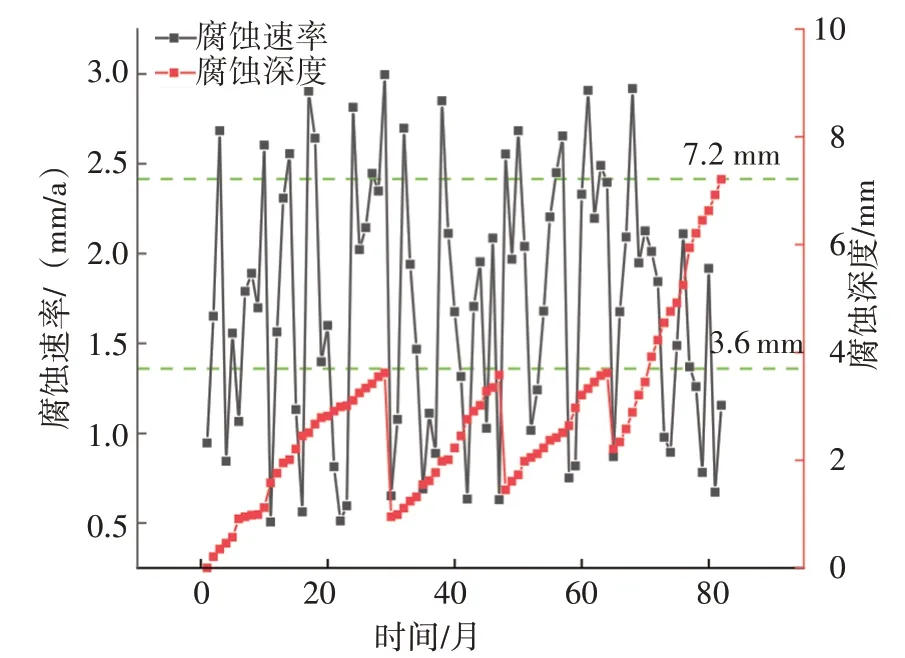
图3 原始腐蚀数据

3.2 腐蚀速率回归模型的确定

在测试腐蚀数据的同时，通过气相色谱分析气质组分，结合输送压力确定酸性气体分压；通过流量计和管径确定流速；通过罗斯蒙特248HAI5N0NS 型温度变送器获取温度参数，结果见表1。

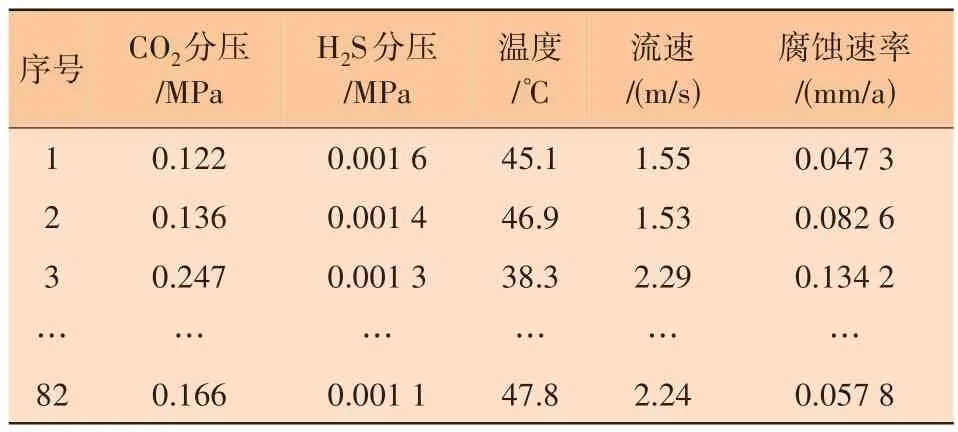
表1 不同监测时间的参数数据

图4 不同影响因素的箱线图

利用Origin 软件，通过多元非线性拟合得到腐蚀速率模型为：

该模型预测值与实际值相比，相对误差范围为[0.21%,4.35%]，相关系数0.984 6，整体误差较小，可以作为剩余寿命预测的基础参数。

3.3 参数估计

结合式（1）和式（9）可知，需求解的参数有a、b、λ0和σB。其中ηi可根据每次预防性维护后的残余壁厚确定，再通过对数极大似然估计法计算a、b，见表2。λ0和σB采用马尔科夫链-蒙特卡洛方法中的Gibbs 抽样法进行参数估计，其中θ取3.2 节中的结果，初始设置λ0服从正态分布，λ0～N(0.01,10)，σB服从伽马分布，λ0～Ga(0.01,10)，迭代样本数为10 000，随机选择其中500个样本进行迭代，Gibbs迭代轨迹见图5。

表2 参数a、b的估计结果

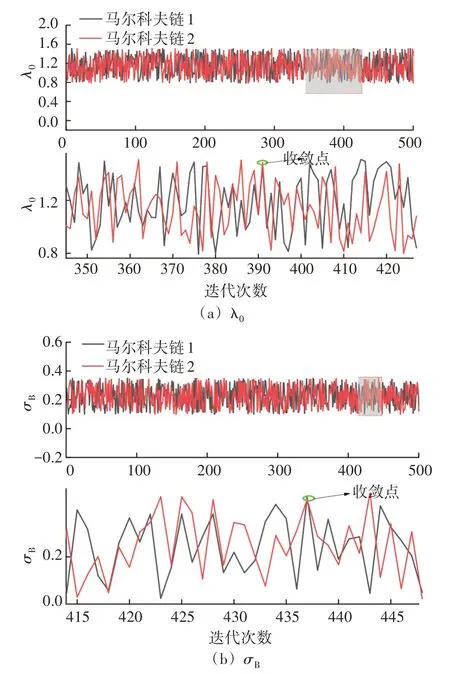
图5 λ0和σB的迭代轨迹

对于λ0，不同初值相互独立的两条马尔科夫链在第390次迭代时收敛到了一起；对于σB，两条马尔科夫链在第437次迭代时收敛到了一起，通过核密度估计确定参数模拟结果，见表3。

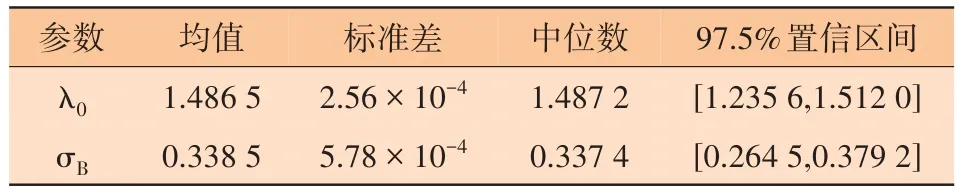
表3 参数λ0和σB的估计结果

3.4 预测结果对比

分别选取32 个月和53 个月作为腐蚀管道剩余寿命的检测估计时刻，由图3可知，32个月时已经完成了1 次预防性维护，根据公式E（Lij）= （w-Xij）/（ci·λ0） = （7.2-1.11）/（0.240 9 × 1.486 5）=17.004（其中ci为经历第一次维护后的腐蚀速率变化因子，取维护前、后腐蚀速率的变化值），可知此时剩余寿命的期望值为17.0 个月，同理53 个月时已经完成了2次预防性维护，剩余寿命的期望值为15.2 个月。将本文3.2 节和3.3 节确定的参数代入式（9）求得概率密度函数（方法1），并与不考虑维护的方法（方法2）、考虑修复如新的方法（方法3）的结果进行对比[8]，见图6。方法1 的概率密度函数值最大，说明数据的集中性较好，剩余寿命的期望值与峰值接近，体现了预测的准确性。其余两种方法显示期望值在密度函数的边缘或侧缝处，说明预测效果较差，方法2没有考虑维护对管道性能的改善，管道退化过程为一条指数曲线，这会低估管道的剩余寿命，导致维护或换管操作提前；方法3 设定每次维护后的腐蚀深度均从0 mm 开始，修复率为100%，但实际情况很难保证100%修复，这会高估管道的剩余寿命。此外，与32 个月的检测估计时刻相比，53 个月的概率密度函数的标准差更小，体现为函数图形集中，且预测值与期望值之间的距离逐渐减小，说明数据量的增加有利于减小误差。

图6 不同检测估计时刻的管道剩余寿命概率密度函数

随后，继续考虑其余维护周期内的剩余寿命预测，结果见表4。

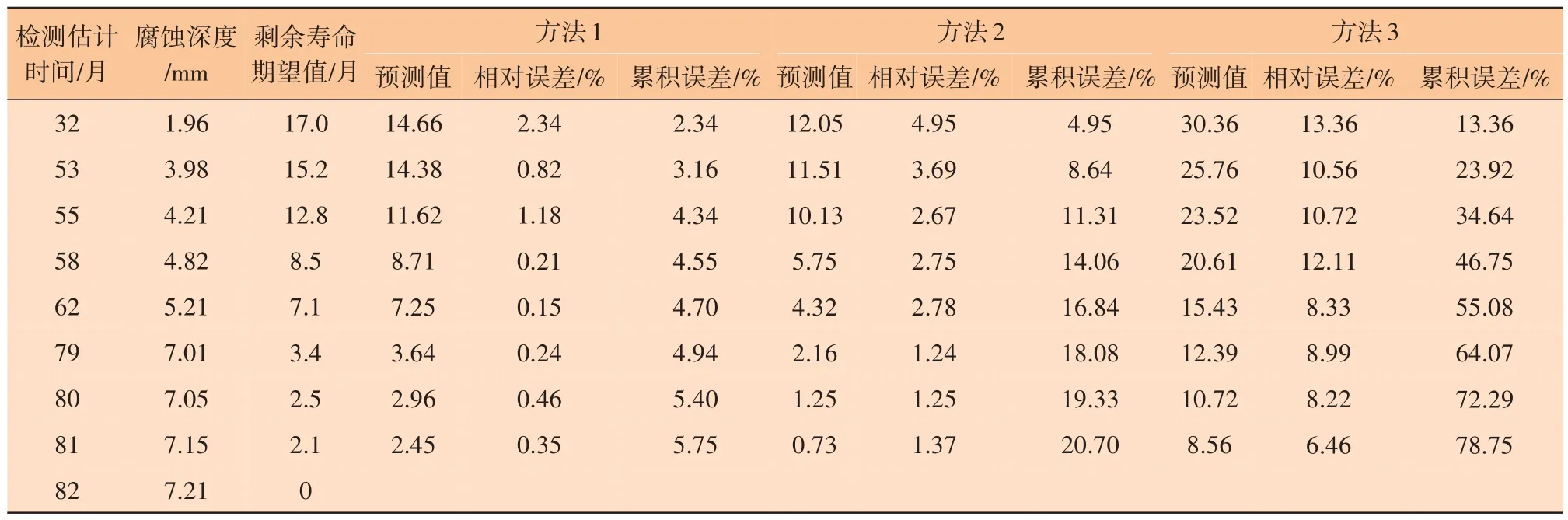
表4 三种方法的剩余寿命预测值与期望值对比

当检测估计时间为81 个月时，方法2 和方法3虽然相对误差逐渐减小，但累积误差增速较快，分别达到了20.70%、78.75%，说明在管道寿命周期内，这两种方法会造成管道提前或延迟维护，造成不必要的经济损失；方法1 的累积误差为5.75%，剩余寿命预测值可更加准确地拟合实际剩余寿命，说明了考虑不完全维护作用具有必要性，该方法与工程实际的符合性较好。

为验证本文模型（方法1）的有效性，将如式（11）所示的常规基于腐蚀速率的剩余寿命预测方法与其进行对比[12]，结果见图7。