分割式赛汝生产系统激励评价

摘" 要： 突发事件及随机冲击影响了管理情境，对时序动态综合评价方法有效性提出了新要求。外部环境复杂多变使得一类时序动态综合评价值波动显著异于以往状态，如评价值出现骤跌然后缓慢爬升至较低水平并持续波动，此时被评价对象的评价值已经击穿经典双激励控制线的负激励线并持续处于下行状态，从而使得经典激励评价方法有效性有待改进。面对这种情况，提出具有情境调节特征的递归激励评价方法，针对分割式赛汝（SERU）生产系统的员工特征，首先通过对赛汝多能工的生产状态进行马氏过程预测，预测出多能工下一生产状态的概率分布，根据得到的概率分布得出每一阶段的递归值并且结合双激励线方法对多能工的递归值进行激励评价，最后结合犹豫模糊函数求解具有隶属度的时间权重，得到具有隶属度时间权重的评价值。通过考虑结合赛汝生产系统这一时代新型生产系统，证明该方法具有更好的柔性和鲁棒性。

关" 键" 词： 综合评价； 情境调节； 赛汝系统； 犹豫模糊； 时间权重

中图分类号： C934""" 文献标志码： A""" 文章编号： 1674-0823（2024）04-0411-08

收稿日期： 2022-11-14

基金项目： 教育部人文社会科学基金资助项目（2019YJC630054）； 国家自然科学基金资助项目（71401109）。

作者简介： 侯" 芳（1980—），女，河北河间人，副教授，博士，主要从事评价理论与技术等方面的研究。

【经济与管理】

DOI：10.7688/j.issn.1674-0823.2024.04.09

一、文献综述

赛汝（SERU）生产是产生于日本生产现场的生产方式，具有及时响应、柔性好、效率高的特点［1］。人力资源成本快速上升是赛汝生产产生的背景之一，因而分析和改进赛汝系统员工绩效评价方法对降低人力资源成本具有一定的现实意义。曾少羽等从多能工工作量公平分配角度出发，以最小化最大工人工作量为决策目标构建了一个公平性导向模型，与传统的效率导向模型相比，该模型在维持较高生产效率的同时实现了多能工间工作量公平分配［2］。任玉红等从赛汝生产系统柔性出发，提出了基于IPO的赛汝系统柔性理论框架，分析了柔性的来源要素和形成机制，研究结果揭示了SERU生产方式高柔性特征的内在机理，通过把握结构柔性和重组柔性两个维度使SERU系统实现低成本高柔性［3］。张哲等通过将模拟退火算法与第二代非支配排序遗传算法相结合形成了一种改进型多目标混合遗传算法，并以最小化最大完工时间及最小化工人的空闲时间为目标，实现了基于多能工配置的赛汝订单调度协同决策［4］。刘畅等通过实证分析发现，团队型组织文化对赛汝生产有显著的正向影响，SERU多能工的运用对企业运营绩效有显著的正向影响，同时环境不确定性加强了这两种影响［5］。王晓晶等以华录松下赛汝生产实践为背景研究了赛汝生产的有效运行和调整修改框架模型［6］。LIU等指出，具有理想技能结构的人才是SERU生产的先决条件，多能工对于SERU生产的成功实施是必不可少的［7］。YIN等提出人才是SERU生产最重要的资源［8］，认为高度专业、训练有素的工人对产品和市场理解较好并能按照一致程序进行操作，有助于实现SERU生产的高效率［9］。综上，赛汝生产系统是一个可划分阶段的动态生产系统，其核心为赛汝多能工。但是当下对赛汝生产系统的研究多考虑对赛汝多能工的调配和系统组建，对赛汝多能工进行绩效评价来调动多能工的生产积极性，而提升赛汝生产系统生产效率的研究较少，同时目前关于在生产过程中通过赛汝生产多能工有效管理方法的研究也有待加强。

相较于传统生产方式，赛汝生产方式具有较高的生产柔性和对任务分配的高度灵活性，具体见表1。因此，赛汝系统对多能工的管理方式与方法直接影响着生产系统运作能否顺利进行。

作为整体性较高的生产系统，赛汝系统可以划分为3个类别，分别为分割式赛汝、巡回式赛汝和单人式赛汝，本文仅对分割式赛汝人员绩效展开激励评价［1］。分割式赛汝适用于赛汝生产系

统初期，属于由流水线生产初步转变为赛汝生产系统，具有半流水线、半赛汝生产系统的特征。分割式赛汝划分为多个生产步骤，赛汝多能工分别完成各自生产步骤，员工激励评价方法设计则主要考虑在生产过程中通过对多能工的生产效率奖惩来提升员工的生产效率。可见，分割式赛汝系统员工工作绩效具有整体性、动态性和激励性特征，应用激励评价方法。

激励评价方法研究已有丰硕成果。易平涛等提出双激励控制线的信息集结方法，对多阶段信息集结引入奖惩机制［10］，随后在状态激励的基础上新增了趋势激励［11］。刘微微等在泛激励控制线的基础上考虑了对被评价对象速度变化进行信息集结，对信息集结提出了新的创新［12］。冯雪丽等在考虑到被评价对象状态变化有效性的基础上，改进了双激励控制方法，引入了激励层级，可以更细粒度地实现对被评价者的激励［13］。李玲玉等在分层激励的基础上，考虑到被评价对象变化趋势不确定性，考虑按比例分层、一维聚类分层和诱导变量分层，并用不同方法对激励层级进行改进［14］。BLUMSTEIN分析了加州能源效率项目评估与基于绩效的项目管理者激励性报酬之间的关系［15］。LI等针对不确定评价问题，将激励管理引入到聚合过程中，提出了一种分位数诱导的不确定重序加权平均（QI-UHOWA）算子，它是分位数诱导的重序加权平均（QI-HOWA）算子的扩展［16］。BLACK探讨了CEO风险承担激励机制的变化与CEO合同中相对绩效评估（RPE）的使用变化之间的关系［17］。上述评价方法是面向具有时序特征问题的管理理论和技术研究，注重根据已有数据趋势和状态分析，通过激励和惩罚控制实现管理意图。

由此本文考虑突发事件对实际管理情境的冲击，尤其是对时序动态综合评价方法有效性提出了新问题。外部环境的复杂多变使得一类时序动态综合评价值波动显著异于以往状态，如评价值出现骤跌后缓慢爬升至较低水平并持续波动，此时被评价对象的评价值已经击穿经典双激励控制线的负激励线并持续处于下行状态，从而使得经典激励评价方法有效性有待改进。本文通过递归特征表示赛汝系统状态，按照不同赛汝员工绩效评价需求，将评价过程分解成相似的系列流程，以马尔可夫过程转移率矩阵刻画赛汝系统状态空间，以马氏过程转移概率得到相应生产状态子集的概率，通过序关系算法对状态子集赋权，得到对应权重，通过状态激励对赛汝多能工实现各阶段工作绩效奖惩激励，通过对各个阶段的评价值递归分析，得到具有情境调节功能的递归评价方法，再进一步结合犹豫模糊，得到具有隶属的时间评价值，进一步帮助企业适应管理情境的变化，以期获得更好的经济效益。

二、原理与方法

1. 研究方法

（1） 递归评价方法

设有m个评价者s1，s2，…，sm，对y个被评价对象按离散时间，在n个时期t1，t2，…，tn进行评价，记si在tj时的评价值为xij=xi（tj），（i=1，2，…，m；j=1，2，…，n），时序评价值矩阵为

X=（xij）m×n=x11x12…x1n

x21x22…x2n

xm1xm2…xmn" （1）

定义1" 对于时间序列xij，序列中xik的评价值只依赖于xik-1的条件分布，且k=2，3，…，n［18］；称这样的序列为Markov列，记为{xij（t），t0}。

规则1" 对于时间序列xij，序列中xik，k∈［1，n］不全是相等的，即时间序列不满足“时齐性”［18］。

由规则1可知，在时间序列中，转移概率矩阵是不相同的。本文确定样本转移概率为pij，即状态Qi转移到状态Qj的概率，设Yij为评价值从状态Qi一步转移到状态Qj的次数，pij=Yij∑bj=1Yij，b为状态个数，j∈［1，n］，可推出一步转移矩阵为

P=p11p12…p1n

p21p22…p2n

pm1pm2…pmn" （2）

令激励评价系统状态数为3，则{xij（t），t0}在不同评价状态U，D，I的转移率矩阵P可以写为分块矩阵：

P=PUUPUDPUI

PDUPDDPDI

PIUPIDPII" （3）

令{Y（t），t≥0}是描述评价系统在U，D，I之间转换的评价过程，是基于马尔可夫过程的聚合过程。假设{Y（t），t≥0}的特性由其马尔可夫核G（t）决定，G（t）是一个转移矩阵，有

G（t）=0GUD（t）GUI（t）

GDU（t）0GDI（t）

GIU（t）GID（t）0" （4）

本文定义QUU（t）=［Upij（t）］U·U=exp（PUUt），式中：Upij（t）=P{评价系统从0到t时刻停留在激励控制线上侧集合U中，时刻t在状态j时刻t在状态i}，i，j∈U；U是集合U中评价值个数，则GUD（t）=QUU（t）PUD，令GUD（t）中的元素为gij（t），i∈U，j∈D，即gij（t）=limΔt→∞P{系统从0到t时刻停留在子集U中，在时刻t到t+Δt离开子集U进入状态j时刻0在状态i}/Δt。

QUU（t）和GUD（t）的Laplace变换为

Q*UU（s）=（sI-PUU）-1" （5）

G*UD（s）=（sI-PUU）-1PUD" （6）

式中：∫∞0gij（t）dt=P{停留在状态j开始于状态i}=g*ij（0），i∈U，j∈D，g*ij（0）∈G*UD（0）。

本文将gij（t）进行归一化，得到标准概率密度函数为

gij（t）∫∞0gij（t）dt=gij（t）g*ij（0）" （7）

令评价系统在4个状态子集中停留时间为Ti（i=U，D，I），其权重为ωi（i=U，D，I），记TU，TD，TI的概率密度函数为fU（t），fD（t），fI（t），其Laplace变换为

f*U（s）=eDPDUG*UD（s）uD" （8）

f*D（s）=eUPUDG*DU（s）uU+eUPUDG*DI（s）uI+

eIPIDG*DU（s）uU+eIPIDG*DI（s）uI（9）

f*I（s）=eDPDIG*ID（s）uD" （10）

式中：e为状态子集的稳态概率；u为列矢量。

评价系统是由三个状态子集集合而成，且其相对应概率密度函数为fU（t），fD（t），fI（t），则可以得到评价系统落在状态子集的概率为密度函数的积分。而被评价者的评价值则由区间权重系数在每个时期的时间权重决定。

根据马尔可夫过程得到的递归值，本文结合实际值得出待评价值，运用马氏矩阵帮助员工在停工停产时期根据以往的状态得到相应的递归值，帮助员工识别自身的努力程度。为了更好地激励和评价，本文对马尔可夫递归值进行激励处理，根据递归值划分激励层级，向上突破当前层级则可以受到更高的奖励，向下跌落当前层级则会受到相应惩罚，通过引进奖惩帮助企业激励追求进步的员工，相应地起到增加员工工作绩效的效果。

（2） 结合赛汝生产系统

在赛汝生产系统中，分割式赛汝是由一个赛汝多能工负责一个生产环节，一个生产产品由多个赛汝多能工组成，这是由于赛汝生产系统初期其多能工的工作能力具有局限性。在分割式赛汝中，由于赛汝生产系统处于组建初期，人员培养尚不完善，本文认为可以考虑减少处在状态区间U的概率，增加处在状态区间I的概率，使更多的员工处于激励较少状态，从而提高员工工作积极性。具体操作步骤如下：由于多能工生产速率各不相同，且不同时间同一多能工生产的速率也不同，本文首先对每一赛汝生产工序或产品赛汝多能工的生产速率进行状态区间划分，考虑每一步骤或产品完成时间不同，对每一工序或产品完成时间进行标准化；其次，确定马尔可夫链的状态空间，采用样本均值方差形式将其划分成为n个状态区间，样本均值为和标准差为s，令D=+ks，以确定各个范围的临界点，即D为各个状态划分的临界点，k是一个可变参数，k∈（-2，2］；根据划分状态层数的不同来调节，以确定各个临界点和状态区间。

2. 奖励层级的划分

规则2" 每一时点的奖惩层级划分方法相同，即每一时点所包含的奖惩层级相同，层级上下界划分原则相同［12］。

规则3" 决策者通过奖惩层级的划分体现大多数的普通被评价者能够享受奖励，极少数优秀被评价者享受更高一级。

本文令被评价对象的递归值X服从正态分布N（μ，σ2）并可进行分层，以μ+0.13σ为第一激励层级线，以μ+0.25σ为第二激励层级线，以μ+1.28σ为第三激励层级线，当被评价值处于区间（μ+0.13σ，μ+0.25σ）时获得第一层正激励，当被评价值处于区间（μ+0.25σ，μ+1.28σ）时获得第二层正激励，当被评价值处于区间（μ+1.28σ，+∞）时，获得第三层正激励，被评价值落在区间（μ，μ+0.13σ）为10%，区间（μ+0.13σ，μ+0.25σ）为10%，处于区间（μ+0.25σ，μ+1.28）为60%，处于区间（μ+1.28，+∞）为20%。第一、二激励层级线μ+0.13σ和μ+0.25σ较容易突破，μ+1.28σ不容易突破，同理得到负激励层级。

规则4" 由于要求正负激励系数和为1且处于不同层级的正负激励系数不同，本文设μ+为正激励系数，μ+1为处于正激励线上方第一层级的正激励系数，μ+2为处于正激励线上方第二层级的正激励系数，μ+3为处于正激励线上方第三层级的正激励系数。即μ+1lt;μ+2，负激励系数同理。为方便计算，本文设2μ±1=μ±2，适度激励则体现为∑31μ++∑31μ-=1。

一般地，对于任一时段［tk，tk+1］，k=1，2，…，n-1，任一被评价对象si的动态综合评价值为两个时间段的连线和横坐标轴所围成的四边形的面积，可表示为

si（tk，tk+1）=∫tk+1tk［yi，k+（x-tk）（yi，k+1-yi，k）/

（tk+1-tk）］dx（11）

本文引入激励控制线之后，在tk+1时刻带有激励的评价值可表示为

y±i，k+1=yi，k+1+y+i，k+1-y-i，k+1" （12）

引入激励后的［tk，tk+1］的动态综合评价值为

s±i（tk，tk+1）=∫tk+1tk［yi，k+（x-tk）（y±i，k+1-yi，k）/

（tk+1-tk）］dx（13）

假设时段［tk，tk+1］被评价对象值穿越到了第n层（n∈［-2，2］），则

y±i，k+1=μ+1y1+μ+2y2+μ+3y3+

μ-1y4+μ-2y5+μ-3y6（14）

式中：yn为被评价对象si处于激励层级的面积。

定理" 在激励评价的规则中，当被评价值为正时，任意带激励的被评价对象的动态综合评价值为正。

证明" 任意一被评价对象si在时段［tk，tk+1］的动态综合评价值为

s±i（tk，tk+1）=∫tk+1tk［yi，k+（x-tk）（y±i，k+1-yi，k）/

（tk+1-tk）］dx（15）

由于y±i，k+1=yi，k+1+y+i，k+1-y-i，k+1，当y-i，k+1=0时，s±i（tk，tk+1）为时段［tk，tk+1］的积分且为正，故定理成立；y-i，k+1gt;0且y+i，k+1=0时，y±i，k+1=yi，k+1-y-i，k+1，但是由于激励系数∑51μ++∑51μ-=1，所以对于激励幅度y-i，k+1，整理可以得到yi，k+1-y-i，k+1gt;0恒成立。同理可以得到y+i，k+1和y-i，k+1都不为0时，定理得证。由于每一期的评价值都是过去的评价值，所以每期的评价值的时间权重都不相同。单纯的叠加求和方式会使得处在进步和退步的员工具有相同的结果，所以本文引入时间模糊数对每一期评价值确定权重，采用厚今薄古的思想。时间模糊数对于处理动态模糊问题具有灵活性的优势，本文从时间维和方案维构成决策信息，通过犹豫模糊数来确定每一时期的权重。以下是对犹豫模糊相关概念的一些定义。

定义2" 设Q是一个给定论域，则Q上的一个时间犹豫模糊集为

A={lt;xi，μtkA（xi），vtkA（xi）gt;xi∈X}" （16）

式中：μtkA（xi）∶X→［0，1］，vtkA（xi）∶X→［0，1］且满足0≤μtkA（xi）+vtkA（xi）≤1，x∈X。

πtkA（xi）=1-μtkA（xi）-vtkA（xi），

πtkA（xi）∶X→［0，1］（17）

式中：μtkA（xi），vtkA（xi）和πtkA（xi）分别为tk时刻A的隶属度、非隶属度和犹豫度函数［19］。

若Q中只有一个元素，则称A为时间犹豫模糊数，记为A=（μtkA，vtkA）。

定义3" 设A={lt;xi，μtkA（xi），vtkA（xi）gt;xi∈X}和B={lt;xi，μtkB（xi），vtkB（xi）gt;xi∈X}为两个时间犹豫模糊数集，则运算法则如下：

AB，当且仅当μtkA（xi）≤μtkB（xi），vtkA（xi）≤vtkB（xi），xi∈X；A=B，当且仅当AB和BA；A的补集AC={lt;xi，vtkA（xi），μtkA（xi）gt;xi∈X}；An={lt;xi，{μtkA（xi），vtkA（xi）}ngt;xi∈X}；A≤B，当且仅当xi∈X。当μtkA（xi）≤vtkB（xi）时，有μtkA（xi）≤μtkB（xi），vtkA（xi）≥vtkB（xi）；当μtkA（xi）≥vtkB（xi）时，有μtkA（xi）≥μtkB（xi），vtkA（xi）≤vtkB（xi）［19］。

定义4" 称映射E∶IFS（X）→［0，1］为直觉模糊熵，若其满足如下条件：

E（A）=0当且仅当A为经典集；E（A）=1当且仅当μA（xi）=vA（xi），xi∈X；E（A）=E（AC）；若A≤B，则有E（A）≤E（B）［19］。

定义5" 函数V为最终评价值，则可以得出

V=∑ni=1wiv（xi）" （18）

式中：wi为时间权重函数。对于时间权重的刻画，本文从两个方面入手，即决策者提供的信息重要性和信息量大小。

本文首先考虑信息量大小即时间直觉模糊熵，构建如下模型：

定义6" 在tk时刻，方案si的时间直觉模糊熵为

E（A）=1n∑ni=1cos［μA（xi）-vA（xi）］［1-πA（xi）］2（19）

由上式定义测度E（A）满足定义4的四个条件可证其是一个直觉模糊熵［10］。如果这个实际值越接近递归后的递归值，那么相应的时间权重越大。

本文对实际值和递归值矩阵进行0-1标准化处理，以降低相关性差异，经过处理的实际值为xmn，递归值为Xmn，则tk时刻实际值Si=（x（tk）i1，x（tk）i2，…，x（tk）in），tk时刻递归值So=（X（tk）o1，X（tk）o2，…，X（tk）on），构建时间权重模型为

Min∑ni=1D（Si，So）

s.t.∑pk=1w（tk）=1" （20）

式中：D（Si，So）=1n∑ni=1（tkon-xmn）2，是递归值So和实际值Si在tk时刻的标准欧式距离，tkon=1n∑nk=1wtkX（tk）mn。

综合直觉模糊熵和递归值期望，则可以集成权重模型为

Min∑ni=1D（Si，So）+（1-η）∑ni=1w（tk）E（A）

s.t.∑pk=1w（tk）=1（21）

式中：η为决策者对两种因素的偏好程度。

3. 评价步骤

步骤1" 根据时序评价矩阵和马尔可夫过程进行矩阵的转移，得到转移的状态子集概率密度函数。

步骤2" 根据状态子集结合权重得出转移后的递归值，结合赛汝生产的特性，选择符合特性的动态评价方法，得到具备奖惩特性的动态评价值。

步骤3" 由于每一期动态评价值都在不同时间，故引入时间直觉模糊数得到每一时期的最佳时间权重。

步骤4" 结合时间权重和动态评价值，得出最后的具有时间权重的评价值，进行比较。

三、算" 例

假设在一个赛汝生产系统中有s1，s2，…，s66位员工，以下算例以分割式赛汝为例，生产方式为U型结构，且在赛汝生产系统中负责不同的生产环节，单人式赛汝同理，6名员工负责6个单独的赛汝，每个员工负责一个产品生产的全过程。本文对6名员工近10个月的绩效考核表进行0-1标准化，并对其放大10倍进行评价，结果如表2所示，得出递归值评价结果如表3所示。

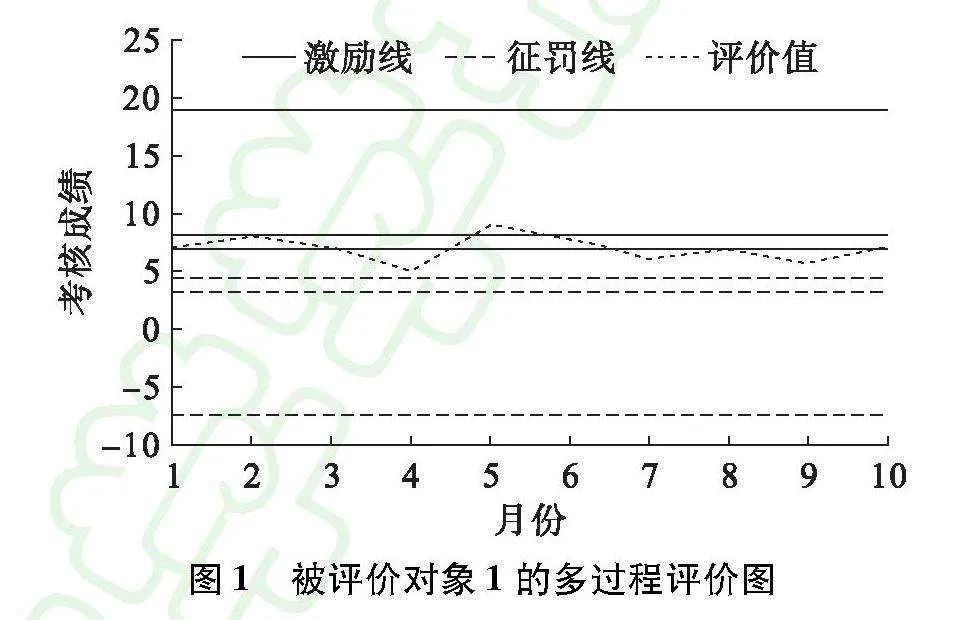
本文对6位员工的递归评价值进行正态分布分析，6位员工的总体数值符合X服从N（5.75，105.15）的分布，第一正激励层级线为7.08，第二正激励层级线为8.31，第三层正激励线为18.87，第一负激励层级线为4.42，第二负激励层级线为3.19，第三层负激励线为-7.37。

本文将以上信息集结绘制为图1（以被评价对象1为例）；根据图1中被评价对象1的多阶段信息图可以求解得出，其各时段追踪激励情况如表4所示；被评价对象1各阶段正负激励信息结果如表5所示；重复进行表3、4步骤，将6名被评价对象各阶段激励信息进行归类，结果如表6所示。

根据规则4和表5的正负评价值，本文求出正负激励系数，结合犹豫时间权重、正负激励系数和犹豫时间权重得出总动态综合评价值如表7所示。

由表7可知，运用递归激励的总体动态激励评价值得到的总体排序为“126543”，而未经过递归处理的总体评价值排序为“614325”（“”表示优于）。可见，带有递归激励的被评价值考虑了员工本身的发展变化和趋势变动，如员工1和6：员工1前期稳定高评价值，后期可能受突发影响一直处于低评价值；经过递归处理考虑员工1在无外界影响情况下的被评价值结果优于员工6，但是未经过递归的被评价值则6优于1。

四、结" 语

本文对被评价对象进行了处理，使其评价值更加具有预测性，评价者可以综合突发因素影响考虑被评价对象的总体表现。并且，本文对被评价对象进行了分层激励，考虑层级激励系数变化，更好地调动员工的积极性。此外，赛汝生产系统要求的员工素质较高，分割式赛汝要求为多能工，而单人式赛汝对员工要求为全能工，要求更高，且在赛汝生产系统下员工高度自治，主观能动性较强，故本文考虑的是通过对员工的绩效进行奖惩激励，调动赛汝多能工的工作积极性。

总体来说，本文考虑对分割式赛汝多能工进行绩效评价和激励，分割式赛汝属于赛汝生产的初期阶段，赛汝员工多为刚进入企业工作的员工，其技术水平相对较低。员工的诉求在于获取更多的薪水，但是面对外部环境复杂多变带来的停工停产，员工的绩效水平较差，甚至是负水平。本文运用马氏过程对员工工作过程进行状态转移分析，借助激励线和时间权重帮助企业更好地对员工进行激励评价，更加符合实际。

参考文献：

［1］唐加福，任玉红，于洋，等.赛汝（SERU）生产与经典生产方式的比较与仿真分析 ［J］.南开管理评论，2021，24（2）：126-134.

［2］曾少羽，吴影辉，于洋.Seru生产系统中面向公平性的多能工-批次-作业分配联合决策研究 ［J］.工业工程与管理，2023，28（2）：58-65.

［3］任玉红，唐加福，王晔.基于IPO系统观的SERU系统柔性的分析框架 ［J］.系统工程理论与实践，2022，42（11）：3030-3043.

［4］张哲，王丽丽，殷勇.基于多能工配置的巡回式赛汝订单调度优化决策 ［J］.南京理工大学学报，2021，45（1）：98-104.

［5］刘畅，李珍，殷勇，等.团队型文化对赛汝（SERU）生产及运营绩效的影响：中国制造业的实证分析 ［J］.系统工程理论与实践，2021，41（2）：431-441.

［6］王晓晶，任玉红，殷勇.赛汝生产有效运行机制：基于华录松下的案例研究 ［J］.系统工程理论与实践，2021，41（2）：455-464.

［7］LIU C G，STECKE K E，LIAN J，et al.An implemen-tation framework for seru production ［J］.International Transactions in Operational Research，2014，21（1）：1-19.

［8］YIN Y，KAKU I，STECKE K E.The evolution of seru production systems throughout canon ［J］.Operations Management Education Review，2008，2（1）：27-40.

［9］YIN Y，STECKE K E，SWINK M，et al.Lessons from seru production on manufacturing competitively in a high cost environment ［J］.Journal of Operations Management，2017，49-51：67-76.

［10］易平涛，郭亚军，张丹宁.基于双激励控制线的多阶段信息集结方法 ［J］.预测，2007，26（3）：39-43.

［11］易平涛，张丹宁，郭亚军.基于泛激励控制线的多阶段信息集结方法 ［J］.运筹与管理，2010，19（1）：49-55.

［12］刘微微，石春生，赵圣斌.具有速度特征的动态综合评价模型 ［J］.系统工程理论与实践，2013，33（3）：705-710.

［13］易平涛，冯雪丽，郭亚军，等.基于分层激励控制线的多阶段信息集结方法 ［J］.运筹与管理，2013，22（6）：49-55

［14］李玲玉，郭亚军，易平涛，等.基于改进分层激励控制线的多阶段信息集结方法 ［J］.东北大学学报（自然科学版），2018，39（1）：148-152.

［15］BLUMSTEIN C.Program evaluation and incentives for administrators of energy-efficiency programs：can evaluation solve the principal/agent problem ［J］.Energy Policy，2010，38（10）：6232-6239.

［16］LI W W，YI P T，GUO Y J，et al.Quantile induced heavy ordered weighted averaging operators and its application in incentive decision making ［J］.International Journal of Intelligent Systems，2018，33（3）：514-528.

［17］BLACK D E.CEO risk-taking incentives and relative performance evaluation ［J］.Accounting and Finance，2020，60（1）：771-804.

［18］王玲娣，任盼盼.带马氏切换扩散过程的指数遍历速率 ［J］.应用概率统计，2020，36（5）：453-466.

［19］姚远.一种基于累积前景理论的直觉模糊动态决策方法 ［J］.数学的实践与认识，2019，49（12）：106-115.

Incentive evaluation of split SERU production system

HOU Fang1，2， CHEN Jiefei1

（1. School of Management， Shenyang University of Technology， Shenyang， Liaoning 110870， China; 2. Northeastern Evaluation Center， Northeastern University， Shenyang， Liaoning 110167， China）

Abstract： Management situation is influenced by unexpected events and random shocks， new requirements are proposed on the effectiveness of time-series dynamic comprehensive evaluation method. The complexity and variability of the external environment makes the fluctuation of a class of time-series dynamic comprehensive evaluation value significantly different from the previous state， such as the evaluation value has plummeted and then slowly climbed to a lower level and continued to fluctuate. At this time， the evaluation value of the evaluated object has penetrated the negative incentive line of the classical dual incentive control line and continued to be in a downward state， which makes the effectiveness of the classical incentive evaluation method to be improved. In the face of this situation， the recursive incentive evaluation method is proposed with contextual adjustment characteristics. For the split SERU production system employee characteristics， through the production state of SERU multi-capable workers through the Markov process of prediction， the next production state of the probability distribution is firstly predicted for the multi-capable workers. Based on the probability distribution， the recursive value is then obtained at each stage， the recursive value of the multi-capable workers is incentivized with the combination of the dual-incentive line method. And finally combined with the hesitant fuzzy function， the time weights are solved with the degree of subordination， and the evaluation value is obtained with time weights with the

degree of subordination. By considering the combination of SERU production system， which is a new production system of the era， it is proved that this method has better flexibility and robustness.

Key words： comprehensive evaluation; situational regulation; SERU system; hesitation ambiguity; time weight

（责任编辑：张" 璐）