热固耦合下采煤机行走轮力学特性研究

张 丹，马克洲，吴卫东，刘训涛，赵跃超，冯业瑞

黑龙江科技大学机械工程学院 哈尔滨 150022

为适应煤矿生产的需要，采煤机不断朝着重载、高强度、高可靠性的方向发展[1]。行走轮负荷随着采煤机功率不断增大而增大，导致行走轮运行过程中由发热所引起的力学性能下降的问题愈发不容忽视。行走轮温度升高，导致轮齿产生热变形，影响轮齿应力，这种温度与应力的相互作用形成了热固耦合场。针对行走轮的热固耦合问题，我国学者以理论研究、试验及数值模拟等方式研究齿轮的热固耦合场，分析耦合场对齿轮力学特性的影响。一些学者利用有限元方法，对热边界条件、摩擦热流密度、对流换热系数等进行计算，得到齿轮温度场分布，并分析温度场对齿轮力学特性的影响[2-7]；有些学者采用控制变量法、直接耦合法、间接耦合法等得到齿轮温度场，分析初始环境温度、齿轮啮合速度、加速度等对轮齿温度与应力的影响规律[8-13]。目前对于齿轮的温度场和热固耦合理论研究已基本成熟，但关于行走轮与销排非共轭啮合形成的热固耦合场对齿面温度、齿面接触强度、齿根弯曲强度等方面影响的问题，尚未完全解决。笔者通过仿真分析的方法，得到行走轮热固耦合场，并研究热固耦合场对采煤机行走轮力学特性的影响，为采煤机行走轮进一步的结构优化设计提供了理论依据。

1 行走轮受力分析

采煤机行走轮压力角为α，分度圆直径为d，行走轮与销排接触齿面受到法向力的作用，将法向力Fn分解为沿水平和竖直方向的力，即切向力Ft和径向力。齿销啮合过程中，齿面各个啮合点速度方向都不相同，因此齿面之间相对滑动产生滑动摩擦力Ff，受力分析如图1 所示。

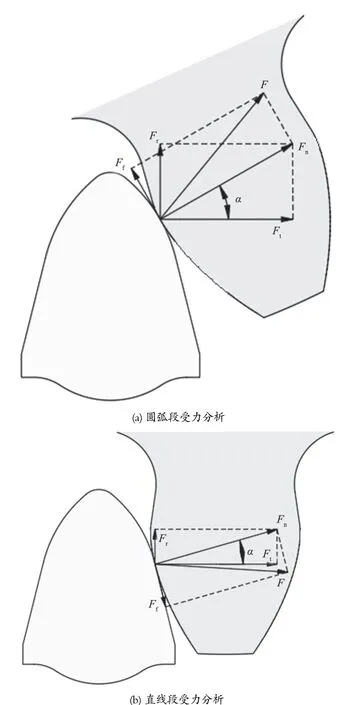
图1 行走轮受力分析Fig.1 Force analysis of walking wheel

由图1 受力分析可知，摩擦力Ff、径向力Fr、切向力Ft、法向力Fn分别表示为

式中：f为齿面摩擦因数；α为压力角，(°)；T为电动机输出转矩，N·m；d为行走轮分度圆直径，m。

2 行走轮应力仿真分析

2.1 载荷的施加与约束

将MG650/1605-WD 型采煤机行走轮三维模型导入 ANSYS Workbench 中进行瞬时动力学分析，接触类型为面面接触，摩擦因数为 0.1，对行走轮施加转矩，转矩为 76 kN·m。

2.2 仿真结果分析

经仿真得出采煤机行走轮单齿啮合过程用时 0.84 s，齿面接触应力云图如图2 所示。

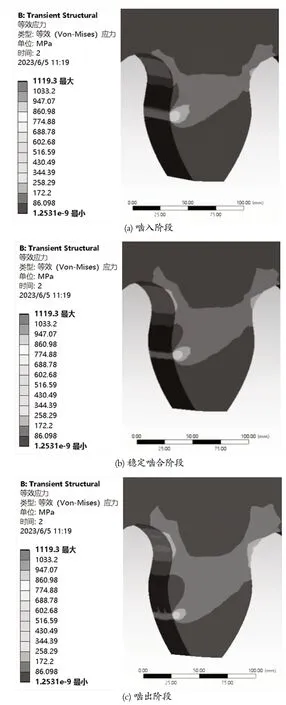
图2 齿面接触应力云图Fig.2 Contact stress contours of tooth surface

由图2 可知，轮齿与销齿在标准工况下啮合时，从行走轮节圆略下开始啮入直至销齿直线段啮出，啮合过程中接触应力呈条状分布，最大接触应力靠近行走轮端面，这是因边角未处理产生的部分应力集中。啮入和啮出阶段，齿面接触应力较小；稳定啮合阶段，在销齿节线位置，接触应力达到最大 991 MPa。

分析行走轮轮齿与销排销齿 2 s 内的啮合接触情况，得出行走轮接触应力曲线如图3 所示。2 s 内 2个齿面完成啮合，接触应力呈周期性变化。初始啮入阶段，行走轮接触应力产生了明显的应力突变，这是由于轮齿脱离上一个销齿，进入单齿啮合，啮合不平稳导致的，可以通过增加齿销啮合重合度来提高平稳性；稳定啮合阶段，行走轮与销排为单齿啮合，接触应力先上升再下降；啮出阶段，行走轮退出啮合，接触应力减小，直至与下一个销齿啮合。

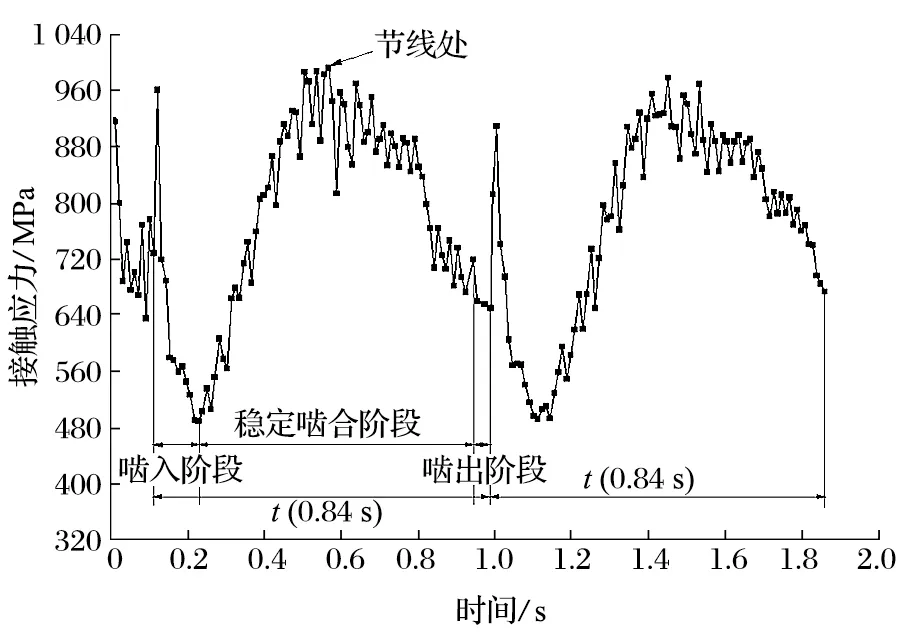
图3 行走轮接触应力曲线Fig.3 Contact stress curve of walking wheel

分析行走轮单齿从啮入到啮出的齿根弯曲应力，获得啮入阶段、稳定啮合阶段、啮出阶段时齿根弯曲应力云图，如图4 所示。齿销啮合过程中，弯曲应力主要集中在齿根过渡圆角处，呈条状分布。

分析行走轮 2 s 内的啮合接触情况，得出行走轮齿根弯曲应力曲线如图5 所示。初始啮入阶段，由于啮合不平稳而导致弯曲应力突变，随后稳定在 235 MPa 左右；稳定啮合阶段，弯曲应力随着时间的增长逐渐增大，在啮合到销齿节线位置时，弯曲应力突变，这是由于齿销啮合经过销齿节线，啮合线由圆弧过渡为直线造成的，在进入啮出阶段前弯曲应力达到峰值 358.65 MPa；啮出阶段，弯曲应力急速下降，这是由于该阶段轮齿己旋转啮出。

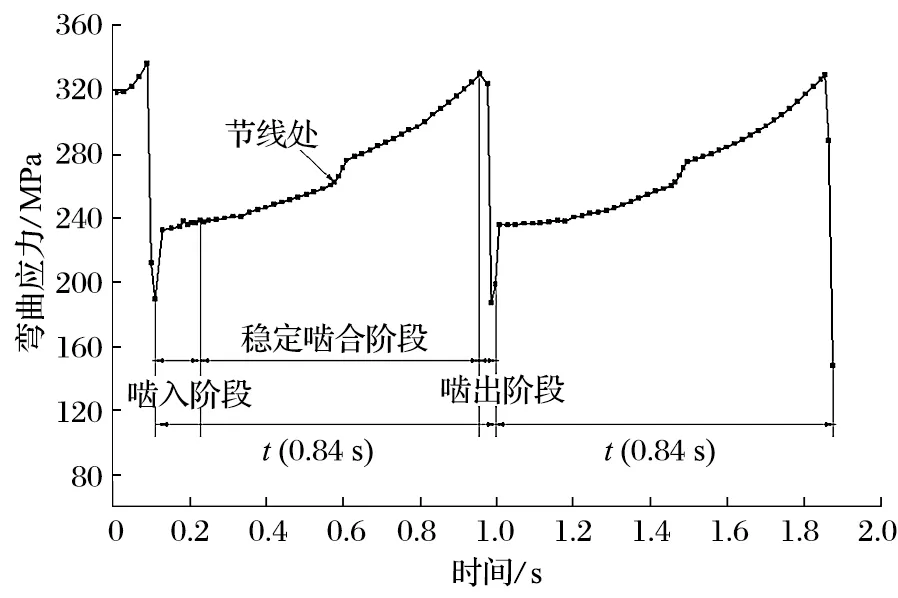
图5 行走轮弯曲应力曲线Fig.5 Bending stress curve of walking wheel

3 行走轮稳态温度场分析模型

轮齿与销齿啮合过程中，轮齿齿面与销齿齿面之间产生相对滑动，因滑动摩擦而产生热量，同时轮齿还与空气之间存在对流换热。行走轮属于低速重载齿轮，由低速重载齿轮温度场所引起的显著热应力不能忽视，热应力对低速重载齿轮传动性能和相关结构设计存在重要影响[15]。

3.1 行走轮轮齿与销排销齿的相对滑动速度

行走轮与销排齿销分为非共轭啮合的圆弧段与共轭啮合的直线段，在计算其相对滑动速度时，圆弧段啮合点的相对滑动速度公式难以直接推导，因此采用图解法的方式，每隔 0.2 mm 距离选取一个点，使其与销齿的轮廓相切，得到非共轭啮合的圆弧段啮合点水平方向与行走轮啮合线之间的夹角α1，共轭啮合的直线段啮合点水平方向与行走轮啮合线之间的夹角α1′=14°，如图6 所示。

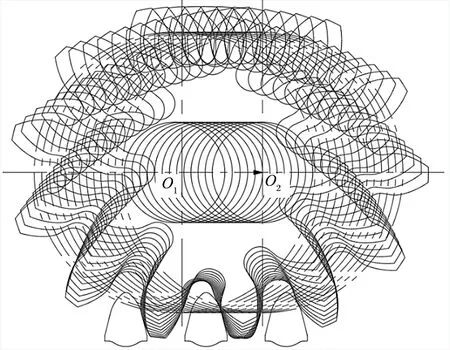
图6 齿销啮合轨迹Fig.6 Meshing trajectory of tooth and pin

行走轮轮心速度

式中：rk1为轮心到啮合点的距离，mm；ω为转动角速度，rad/s；θ1为啮合点线速度与水平方向夹角，(°)。

对比分析从O1到O2一个周期内理论轮心的速度曲线与实际速度曲线，如图7 所示。

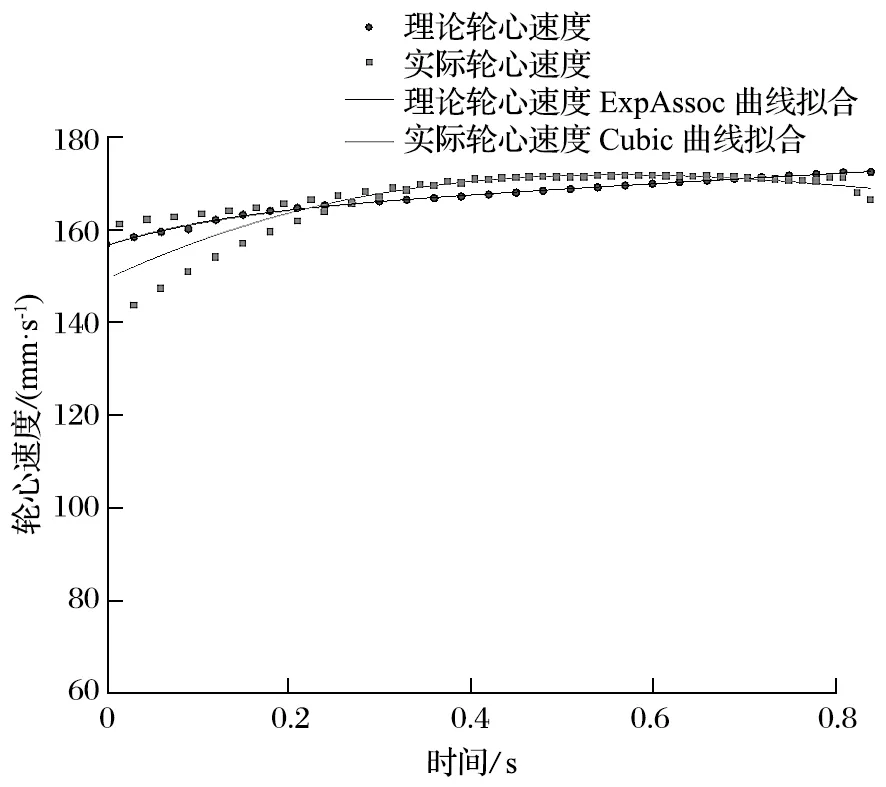
图7 行走轮轮心速度曲线Fig.7 Velocity curves of walking wheel center

由图7 可知，轮心实际速度波动在开始啮入时较大，且峰值大于理论轮心速度，这是由于啮入不平稳造成的。行走轮实际轮心速度先升后降，而理论轮心速度持续上升，这是由于实际轮心速度受到齿销非共轭啮合的影响，产生波动。理论与实际轮心平均速度都为 167 mm/s。

齿销啮合与齿轮齿条类似，其啮合点切线方向绝对滑动速度不同，导致轮齿相对滑动，啮合齿面间存在摩擦，产生摩擦热。由此可见，轮齿间相对滑动速度是生成热量的主要因素之一。相对滑动速度计算示意如图8、9 所示。

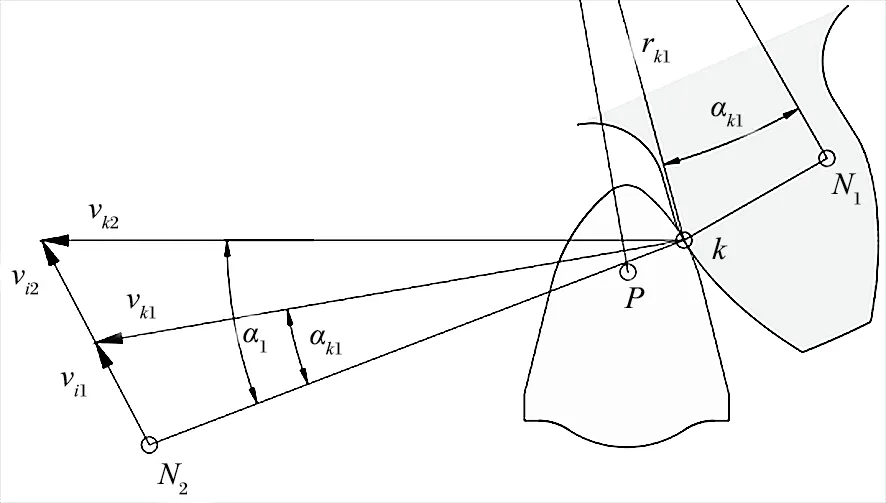
图8 圆弧段相对滑动速度计算示意Fig.8 Calculation of relative sliding velocity of arc segment

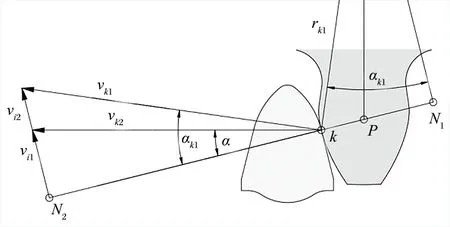
图9 直线段相对滑动速度计算示意Fig.9 Calculation of relative sliding velocity of line segment

式中：r为轮齿节圆半径，mm。则啮合点处绝对速度

啮合点处滑动速度

销齿圆弧段、直线段啮合点处绝对速度

销齿圆弧段、直线段啮合点处滑动速度

行走轮与销排相对滑动速度

以一个轮齿为分析对象，得到啮合点的相对滑动速度如图10 所示。

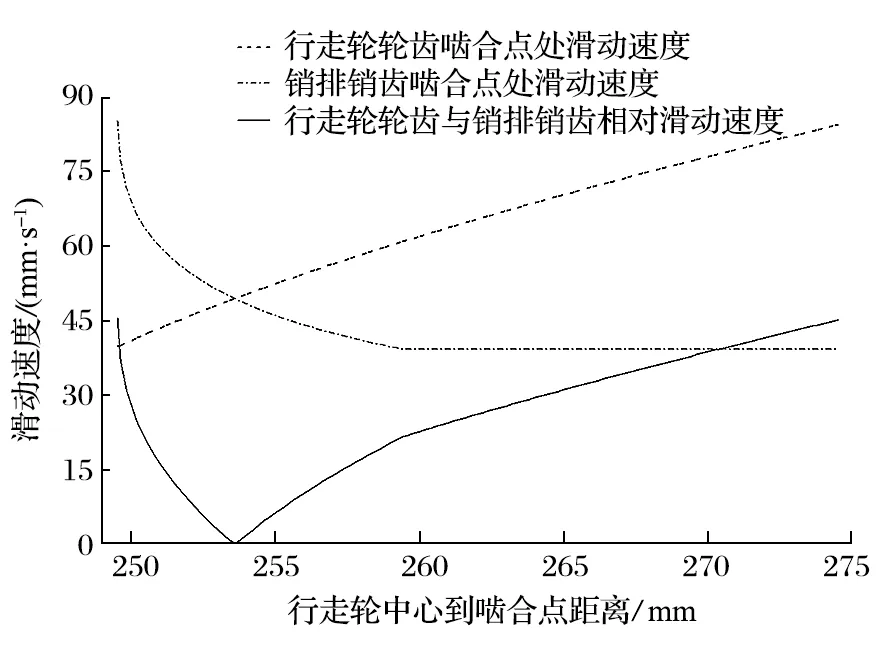
图10 轮齿与销齿的相对滑动速度计算示意Fig.10 Calculation of relative sliding velocity of gear teeth and pin teeth

由图10 可知，轮齿啮合点处滑动速度从啮入到啮出持续增大，速度曲线光滑，不受销齿曲线过渡的影响。销齿啮合点滑动速度持续减小，速度曲线过渡为直线，这是由于齿销啮合从圆弧段向直线段过渡，啮合点切线与水平方向角度转变为定值 14°形成的。轮齿与销齿相对滑动速度从啮入到啮出先减小后增大。

3.2 行走轮摩擦热流密度与对流换热系数

行走轮轮齿齿面的摩擦热主要由啮合齿面滑动摩擦产生，在运行过程中啮合齿面的接触压力大小不同、分布不均，所以其不同位置产生的摩擦热沿各个齿面的分布是不均匀的。

行走轮在啮合点处产生的摩擦热流密度[16]的计算公式为

式中：qc为任意啮合点的摩擦热流密度，W/m2；β为行走轮轮齿的摩擦热分配系数；r1为摩擦能转化为热能的系数，一般取r1=0.90～0.95；σ为啮合点的接触应力，Pa；v为齿面啮合点的相对滑动速度，m/s。

将相对滑动速度以及接触应力等数值代入式(12)，可计算得到行走轮的摩擦热流密度。

行走轮在运行过程中，轮齿在每个旋转周期内都与销齿啮合接触一次，获得一次热载荷，因此计算时，应将每个周期生成的摩擦热流密度作平均化处理[17]，得到摩擦热流密度曲线如图11 所示。

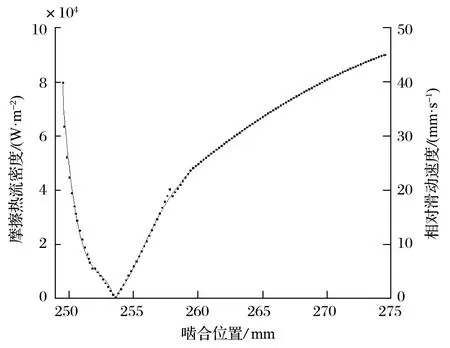
图11 啮合点的摩擦热流密度曲线Fig.11 Friction heat flux density curve of meshing point

式中：t为行走轮转动周期，s ；l为单齿啮合的啮合线长度，mm。

行走轮与销排为开式齿轮传动，啮合齿面摩擦为干摩擦。行走轮啮合传动过程中对流换热是空气介质与轮齿之间的换热，主要通过空气相互混合方式换热，因此轮齿各个面对流换热系数取空气的对流换热系数[18]。

3.3 行走轮齿面理论温升

根据 Blok 理论[19]，可求出行走轮在各个啮合点的瞬时温升，轮齿最大瞬时温升

式中：Fnb为单位长度啮合线法向力，N；b为接触齿宽，m；λ1、λ2为轮齿密度，kg/m3；γ1、γ2为轮齿导热系数，W/(m·K)；c1、c2为轮齿比热容，J/(kg·K)。

3.4 稳态温度场仿真结果

运用有限元软件 ANSYS 进行温度场仿真分析，得到轮齿温度分布如图12 所示。

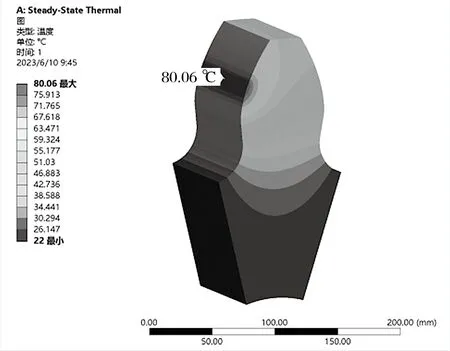
图12 轮齿温度仿真Fig.12 Simulation of wheel tooth temperature

由图12 可知，行走轮温度呈条状分布，这是由于行走轮对流换热对象主要以空气为主，对流换热系数小，在啮合齿面内热量流失慢。行走轮轮齿最高温度为 80 ℃，位于行走轮齿宽中部，且分布在行走轮分度圆附近。

4 耦合场下的行走轮的力学特性

对比分析行走轮热固耦合场与非热固耦合场接触应力、弯曲应力分布规律，如图13、14 所示。

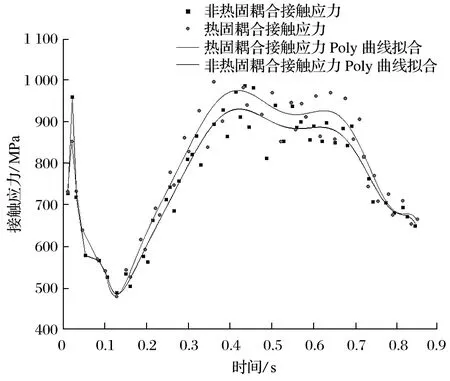
图13 接触应力对比分析曲线Fig.13 Comparative analysis curves of contact stress

由图13 可知，行走轮热固耦合场与非耦合场接触应力分布规律在一个周期内基本相同，热固耦合场接触应力大于非热固耦合场。热固耦合场平均接触应力为 793.9 MPa，非热固耦合场为 779.9 MPa，热固耦合场平均接触应力比非热固耦合场大 14 MPa，增幅为 1.7%，可知热载荷增大行走轮接触应力。热固耦合场中接触应力平均波动率 Δσ/Δt＝4 420.7，非热固耦合场Δσ/Δt＝3 996.3，热固耦合场中接触应力平均波动率Δσ/Δt比非耦合场大 424.4，增幅为 10.6%。这是由于行走轮在热固耦合场中受热变形较大，啮合线偏移，产生较大的应力波动。啮入阶段热固耦合场的应力突变值比非热固耦合场小 107.6 MPa，降幅为 11.2%，这是由于轮齿啮入处温度较低，虽受热膨胀变形，但并未超过弹性变形，抵消部分变形量，降低了冲击力。热固耦合场行走轮最大接触应力为 1 070 MPa，行走轮材料的许用应力为 1 016 MPa[20]，接触应力超出材料屈服强度，易导致轮齿失效损坏。热固耦合场中齿销接触应力的增加，为疲劳破坏产生提供了条件，降低行走轮使用寿命，因此需要通过轮齿修形等方式降低耦合场的影响。

由图14 可知，热固耦合场与非热固耦合场的弯曲应力分布规律以及平均波动率Δσ/Δt几乎相同。在一个周期内热固耦合场弯曲应力高于非热固耦合场，热固耦合场平均弯曲应力比非耦合场大 16 MPa，增幅为 5.9%。行走轮在热固耦合的作用下增大了拉压应力，加剧齿根应力集中，更易导致齿根发生疲劳破坏，降低行走轮使用寿命。

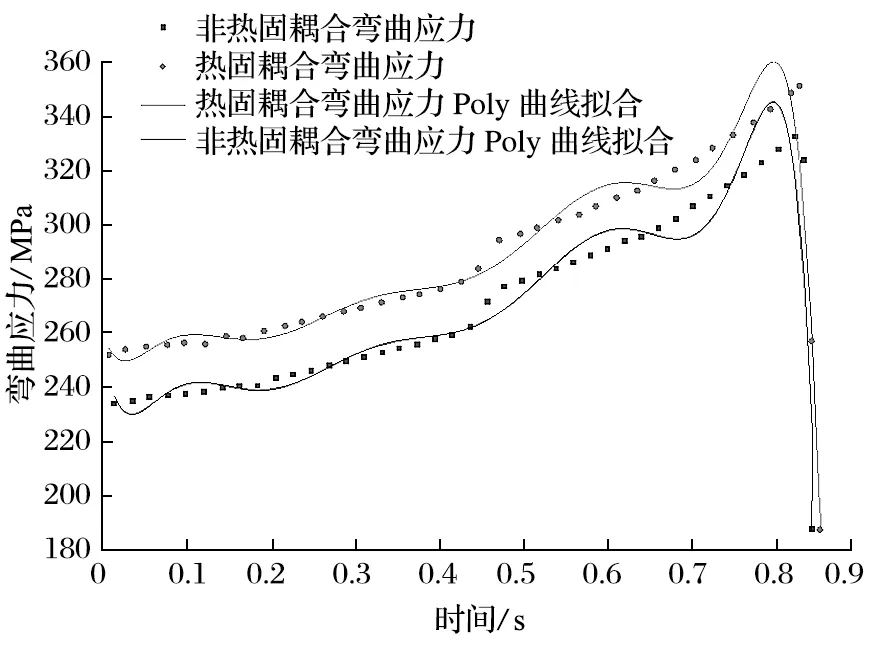
图14 弯曲应力对比分析曲线Fig.14 Comparative analysis curves of bending stress

5 结论

(1) 行走轮接触应力与弯曲应力呈周期性变化，条状分布，最大接触应力靠近行走轮端面，最大弯曲应力在齿根过渡圆角处。行走轮啮入阶段接触应力波动大，啮合不平稳；稳定啮合阶段应力先升再降，最大接触应力在销齿节线处；啮出阶段退出啮合。行走轮啮入阶段弯曲应力波动大，啮合不平稳；稳定啮合阶段应力逐渐增大，销排节线处突变，最大弯曲应力在稳定啮合阶段；啮出阶段弯曲应力急速下降。

(2) 行走轮轮齿与销排销齿的相对滑动速度先减小后增大，摩擦热流密度分布规律与相对滑动速度成正比。

(3) 行走轮轮齿齿面温度呈平面条状分布，行走轮轮齿最高温度为 80.06 ℃，位于行走轮齿宽中部，且分布在行走轮分度圆附近。

(4) 热固耦合场接触应力与弯曲应力大于非热固耦合场，接触应力波动耦合场大于非耦合场，弯曲应力波动几乎相同。热固耦合场中齿销接触应力与弯曲应力的增加，加剧行走轮接触应力的波动与齿根位置的应力集中，为疲劳破坏的产生提供了条件，降低行走轮使用寿命，因此需要通过轮齿修形等方式降低耦合场的影响。