基于误差补偿的RV减速器摆线齿廓二次共轭修形方法
2023-12-29杜雪松刘思奇李昌斌魏沛堂宋海蓝
杜雪松,刘思奇,李昌斌,魏沛堂,宋海蓝
(重庆大学 高端装备机械传动全国重点实验室,重庆,400044)
RV(rotate vector)减速器具有体积小、传动比大、精度高、刚度高等优点,被广泛应用于航空航天、工业机器人等领域[1-4]。作为RV减速器的核心组件,摆线针轮传动对整机的传动精度、传动效率和承载能力有重大影响。为了便于装配和润滑,需对RV 减速器中的摆线轮齿廓进行修形[5-7]。现有的摆线轮修形方法(理论修形方法)中,修形量在设计阶段进行确定,但在工程实践中发现,零部件的不同误差组合可能导致装配干涉或侧隙过大,在批量化生产中进行分组装配时,理论修形方法无法提供有效的分组依据,因此,对于考虑加工误差及其组合的摆线轮齿廓修形方法的研究具有重要的理论和工程应用价值。
目前,国内学者针对摆线齿廓修形问题进行了大量研究,而国外文献较少。李力行等[8-9]建立了包含等距、移距和转角修形的通用摆线齿廓方程,并提出了最佳修形量的计算公式;秦争争等[10]考虑摆线轮弹性变形的影响,提出了一种可以补偿摆线轮弹性变形的摆线轮齿廓修形方法;何卫东等[11]提出了负等距加负移距的摆线轮修形方法,并通过逼近转角修形齿廓建立起优化模型;陆龙生等[12-13]针对摆线针轮回差优化问题,提出一种可以补偿摆线针齿间弹性变形的修形方法,并针对承载优化问题,提出一种新型等距加移距组合修形方法;刘亭亭等[14]提出了一种用摆线齿廓修形补偿零部件尺寸偏差,以回差最小为优化目标的摆线齿廓修形方法,研究了尺寸偏差对机构回差的影响规律,但未给出修形量的确定方法;REN 等[15]提出了一种将摆线齿廓分为多段、每段修形量根据具体的啮合要求来确定的反向修形方法;赵博等[16]提出了一种抛物线修形方法,与传统修形方法相比,修形后的齿廓更加逼近共轭齿廓,在此基础上,柯庆勋等[17]提出一种二阶对数修形方法;李晋凡等[18]基于摆线轮齿廓压力角分布规律,提出一种直线修形方法。以上修形方法虽有一定理论创新,但设计的摆线轮难以加工和测量。
综上所述,以上方法均未考虑零件加工误差的影响,为此,本文作者提出一种可以补偿加工误差的二次共轭修形方法,首先建立了一种误差补偿模型,将零件加工误差通过等距或移距修形量进行等效替换,进而确定一次修形量,得到理论零侧隙摆线齿廓,然后以给定的径向间隙、回差作为约束条件,通过建立的共轭齿廓优化模型确定二次修形量,得到共轭摆线齿廓。该方法可在零件误差组合条件下对加工误差进行有效补偿,从而满足设计要求。
1 影响RV 减速器传动精度的主要误差
RV 减速器由两级行星齿轮传动机构组成(图1),第一级为渐开线齿轮行星传动机构,第二级为摆线针轮行星齿轮传动机构。渐开线行星传动部分包括输入齿轮轴和行星轮;摆线针轮传动部分包括曲柄轴、摆线轮、针齿、针齿壳、行星架、法兰盘等。
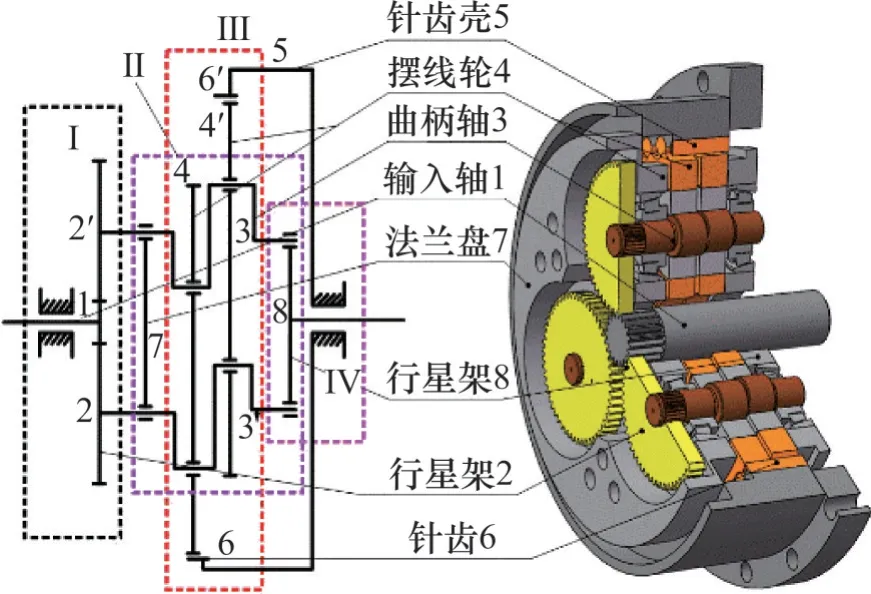
图1 RV减速器传动原理图Fig.1 Principle diagram of RV reducer transmission
现有文献研究结果表明[12,19-20],第二级摆线针轮传动相比第一级渐开线行星传动对整机传动精度的影响大得多,摆线针轮传动各误差敏感性指数如图2所示。从图2可以看出:针齿壳中心圆半径误差、针齿半径误差、针齿销孔圆周位置度误差对RV减速器的传动误差影响较大。现有的加工技术可以较好地控制摆线轮周节累计误差、等距修形误差和移距修形误差[19],故本文主要针对针齿壳中心圆半径误差、针齿半径误差、针齿销孔圆周位置度误差的补偿展开研究。
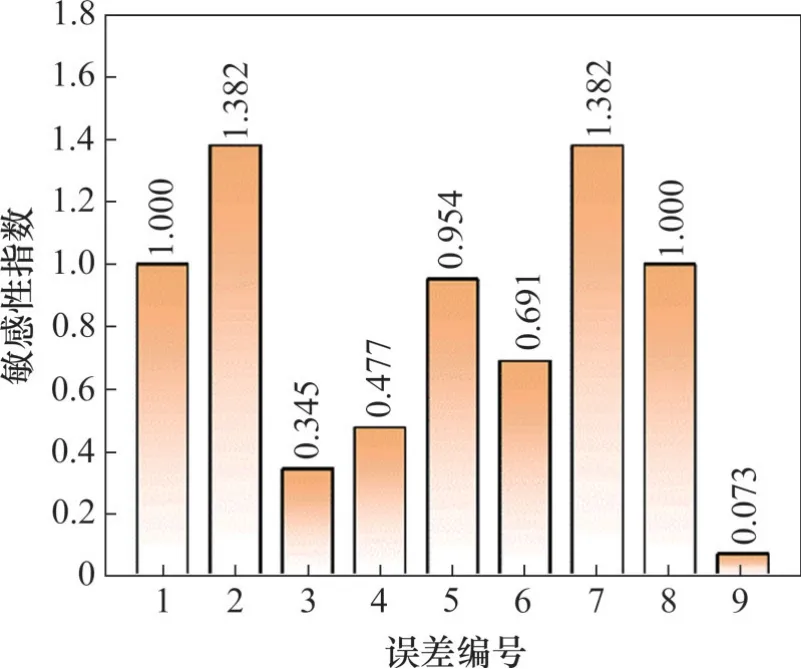
图2 摆线针轮传动各误差敏感性指数Fig. 2 Error sensitivity indices of cycloid pin wheel drive
2 基于误差补偿的摆线齿廓二次共轭修形方法
2.1 误差补偿模型及一次修形量确定
2.1.1 对针齿半径误差δrrp的补偿
针齿半径误差补偿原理如图3 所示,图中,op、oc分别为针轮和摆线轮的中心点,rp为针齿壳中心圆半径,a为曲柄轴偏心距。当针齿半径rrp存在正偏差时,针齿与摆线轮之间会产生干涉,为消除干涉且实现零侧隙,摆线轮可采用正等距修形;同理,当针齿半径rrp存在负偏差时,针齿与摆线轮之间会产生间隙,可对摆线轮进行负等距修形补偿间隙。
2.1.2 对针齿壳中心圆半径误差δrp的补偿
针齿壳中心圆半径误差补偿原理如图4 所示。当针齿壳中心圆半径rp存在正偏差时,针齿与摆线轮之间会产生间隙,摆线轮可采用正移距修形补偿间隙;同理,当针齿壳中心圆半径rp存在负偏差时,可对摆线轮进行负移距修形消除干涉。

图4 针齿壳中心圆半径误差补偿原理Fig. 4 Error compensation principle of center circle radius of needle tooth shell
2.1.3 对针齿销孔圆周位置度误差δt的补偿
针齿销孔圆周位置度误差补偿原理如图5 所示,当针齿销孔圆周位置度误差δt为正偏差时,针齿与摆线轮之间会产生干涉,摆线轮可采用正等距修形;同理,当针齿销孔圆周位置度误差δt为负偏差时,针齿与摆线轮之间会产生间隙,可对摆线轮进行负等距修形。
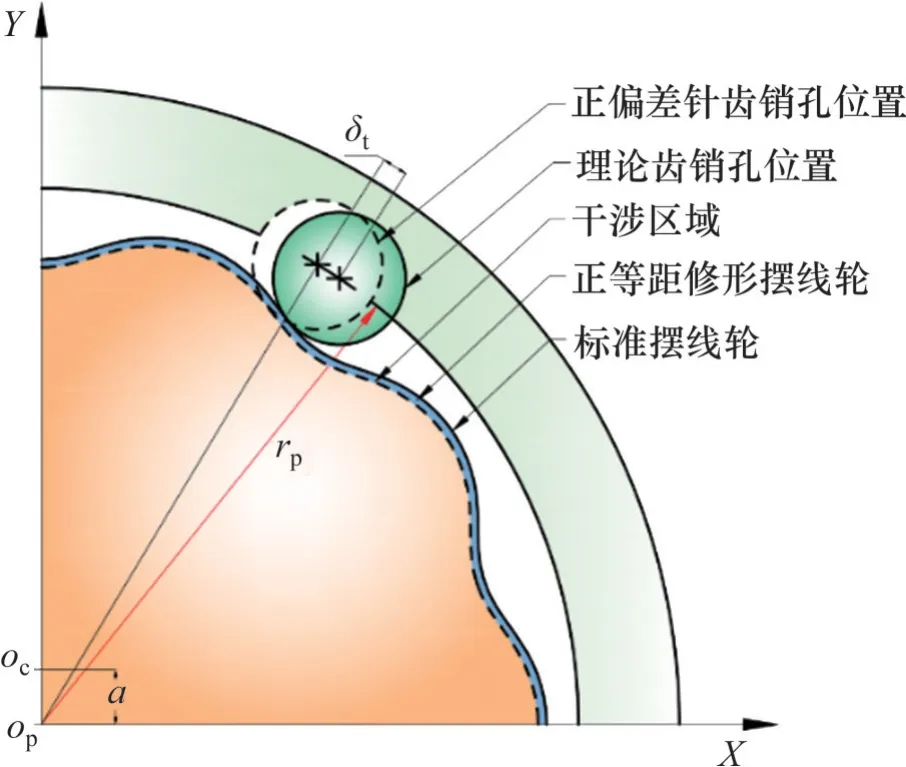
图5 针齿销孔圆周位置度误差补偿原理Fig. 5 Compensation principle of pinhole circumferential position error
2.1.4 一次修形量的确定
通过以上分析可以看出,各误差可利用等距或移距修形方式进行补偿。误差补偿量可以通过将误差在摆线轮分布圆上引起的圆周侧隙等效替换为相应的等距和移距修形量来确定。各因素在分布圆上引起的圆周侧隙如下[20]:
式中:jD、js、jrp、jt、jp分别为等距修形Δrrp、移距修形Δrp、针齿半径误差δrrp、针齿销孔圆周位置度误差δt、针齿壳中心圆半径误差δrp在摆线轮分布圆上引起的圆周侧隙;k为摆线轮移距修形时的短幅系数,k=azp/(rp+Δrp)。
进行补偿时,令jrp=jD,jt=jD,jp=js,便可求得单项误差的补偿修形量。表1给出了补偿各单项误差所采用的修形方式和补偿修形量。
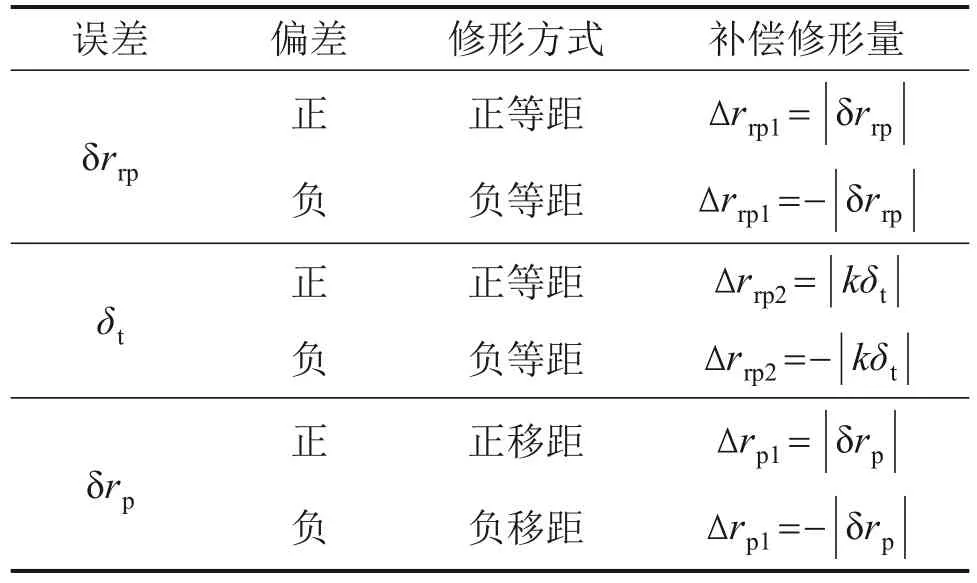
表1 单项误差补偿的修形方式和补偿修形量Table 1 Modification mode and compensation modification amount corresponding to single error compensation
在实际工程中,各误差是组合出现的,摆线齿廓总补偿修形量为各单项误差补偿修形量的代数和,由此可得一次修形的总修形量为:
式中:Δrrp1、Δrrp2、Δrp1分别为针齿半径误差δrrp、针齿销孔圆周位置度误差δt、针齿壳中心圆半径误差δrp的补偿修形量。
在负载条件下,摆线轮与针齿间会产生弹性变形。为降低弹性变形的影响,需计算出摆线轮和针齿在接触挤压过程中的形变量函数δ(φ),将其补偿到等距加移距组合修形摆线齿廓方程当中[12]。
式中:φ为针齿相对于转臂的转角;δmax为受力最大的摆线轮齿的弹性变形量。
将式(2)中得到的修形量(Δr′rp, Δr′p)和式(3)的形变量函数δ(φ)代入等距加移距组合修形摆线齿廓方程[8],得到一次修形后的理论零侧隙摆线齿廓方程为:
式中:iH为摆线轮与针轮的相对传动比,iH=zp/zc;zp、zc分别为针轮和摆线轮的齿数;s=1+k2-2kcosφ。
2.2 摆线齿廓二次共轭修形量确定
通过一次修形得到的理论零侧隙摆线齿廓仅具有理论意义,为了便于装拆和润滑,摆线轮齿根、齿顶处需留有径向间隙Δr,必须对该齿廓进行二次修形。摆线轮转角修形可以实现共轭啮合,但无法在齿根、齿顶处形成径向间隙,故二次修形仍采用等距加移距组合修形方法,通过逼近一次修形摆线齿廓啮合工作段来确定二次修形量,进而得到共轭摆线齿廓,该齿廓既能满足径向间隙的要求,又可与针齿实现共轭传动(图6)。
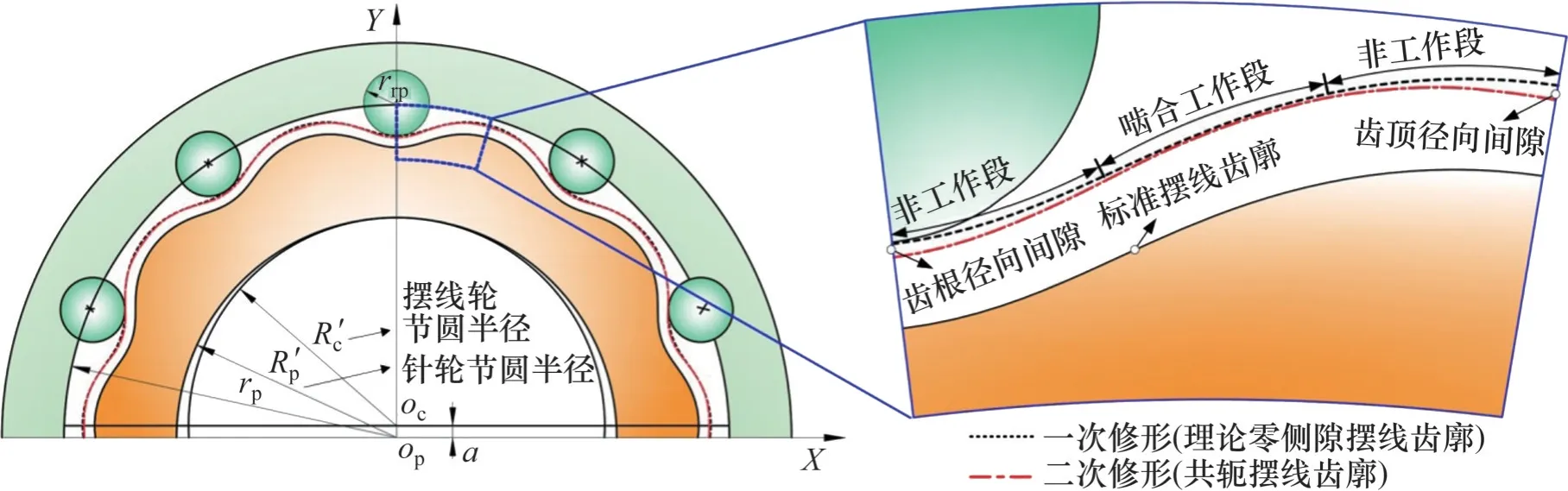
图6 二次共轭修形原理Fig. 6 Quadratic conjugate modification principle
在逼近理论零侧隙摆线齿廓啮合工作段的过程中,工作段上、下界限点的选择可以从传动角度出发,使得工作段内压力角均值最小,此时可求得理论零侧隙摆线齿廓啮合工作段两界限点B′、C′对应的针齿相对于转臂的转角分别为φb和φc[21],两界限点的X轴坐标值为xb和xc(图7),将此工作段在X轴方向上分为m等份,并代入式(4)得到B′C′段上的坐标点集为(x′zi,y′zi)(i=1,2,…,m),给定一组等距加移距组合成二次修形量Δrr*p和Δrp*,可计算出B*C*段上的另一坐标点集为(x*zi,y*zi)(i=1,2,…,m),两个点集Y坐标差绝对值的均值为

图7 二次修形摆线齿廓Fig. 7 Cycloid tooth profile of secondary modification
均值越小,表明两者逼近程度越高。事实上,在有径向间隙的情况下,若要保证二次修形后的齿廓光滑连续,则B′C′与B*C*段齿廓不会重合,在摆线轮分布圆处必然存在圆周侧隙,必须根据回差的设计要求对圆周侧隙加以约束,两齿廓间的圆周侧隙j的计算式为
式中:k1和k2分别为一次修形和二次修形摆线齿廓的短幅系数,k1=azp/(rp+Δr′p),k2=azp/(rp+Δr*p)。
由圆周侧隙j可计算出摆线针轮传动的回差γ为
第二次修形后,摆线轮与针齿在齿根、齿顶处产生的径向间隙Δr为
为满足高精度设计要求,工程中通常约束等距修形量|Δr*rp|≤0.20 mm, 径向间隙0 <Δr≤0.03 mm,回差精度γ≤1′。
综上,建立的二次修形量优化模型为:
用最小二乘法对式(9)进行迭代求解,可求出最佳二次修形量为Δr*rp和Δr*p。
3 实例分析
为验证本文修形方法的正确性,以RV-80E 型减速器为样机建立有限元仿真模型,样机参数如表2所示,其中,修形量为不考虑误差的理论修形量。后续将从传动精度和啮合性能两方面对文中修形方法和理论修形方法进行对比分析。

表2 RV-80E型减速器摆线针轮设计参数Table 2 Design parameters of cycloid pin wheel of RV-80E reducer
3.1 有限元模型的建立及验证
为了提高计算效率,在建立有限元分析模型时,仅考虑第二级摆线针轮传动,包括摆线轮、曲柄轴、针齿壳和针齿等主要承载构件。摆线轮和曲柄轴材料为20CrMnMo,弹性模量为211 GPa,泊松比为0.28;针齿壳和针齿材料为GCr15,弹性模量为219 GPa,泊松比为0.3。摆线轮与针齿、曲柄轴与摆线轮之间的接触为摩擦接触,摩擦因数为0.1;针齿与针轮的接触为绑定接触。针齿壳外圈施加固定约束;摆线轮3个轴承孔内表面与摆线轮圆心OC建立耦合约束,只释放耦合点绕Z轴的旋转自由度和X轴、Y轴的平移自由度;曲柄轴外表面与针齿壳圆心OP建立耦合约束,只释放耦合点绕Z轴的旋转自由度。有限元模型如图8所示。

图8 有限元模型Fig. 8 Finite element model
分析时采用3 个载荷步进行加载:1) 给曲柄轴施加一个微小角位移,使摆线轮与针齿间接触;2) 给单片摆线轮施加负载至额定转矩226.6 N·m[22];3) 给曲柄轴施加360°的角位移。为了提高计算精度,细化摆线针轮接触区域的网格边长为0.04 mm[23],共计262 460个节点。
施加负载后,采用解析法[22]和有限元法计算的摆线轮接触应力分布如图9 所示。从图9 可见:二者结果趋势相符,且最大接触应力都在同一个齿上,最大接触应力相对误差在10%范围内[24]。
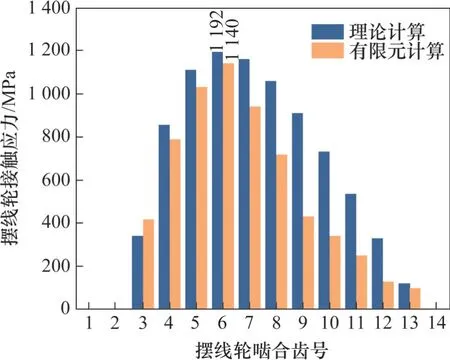
图9 摆线轮接触应力分布Fig. 9 Contact stress distribution diagram of cycloid gear
在不同工作力矩(6.8、56.7、113.3、169.9、226.6 N·m)和载荷下,摆线针轮传动误差及其峰峰值计算结果如图10 所示,可以看出:摆线针轮传动误差峰峰值与载荷呈线性正相关关系,与文献[25]中的相同,表明了本文所建有限元模型的正确性。
3.2 本文修形方法验证
针对样机的误差项设计正交实验,根据表2的设计公差确定误差范围,每个误差项选取3 个水平,误差因素水平如表3所示。
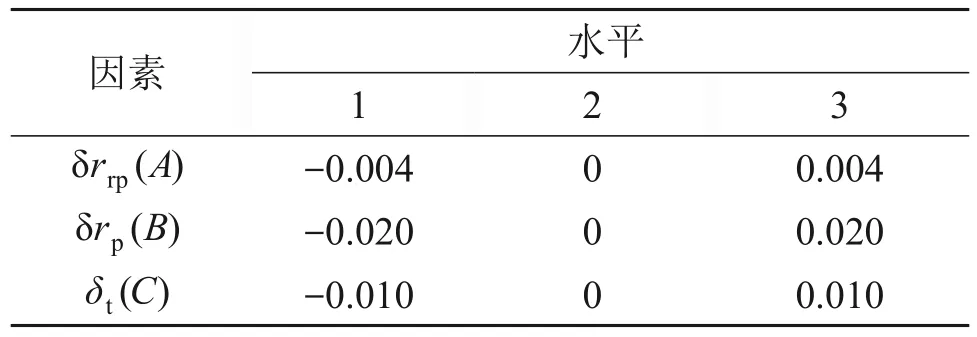
表3 误差因素水平表Table 3 Error factor level tablemm
选取L9(34)正交表安排试验,正交试验方案如表4 所示,建立了9 组试验模型和1 组无误差对比模型(模型10),并给出了每组模型对应的二次修形量。其中,模型2、4、5只包含单项误差,其他模型为多项误差组合。在模型1、4、5、7 的误差条件下,理论修形方法会使摆线齿廓产生干涉,故无计算结果。
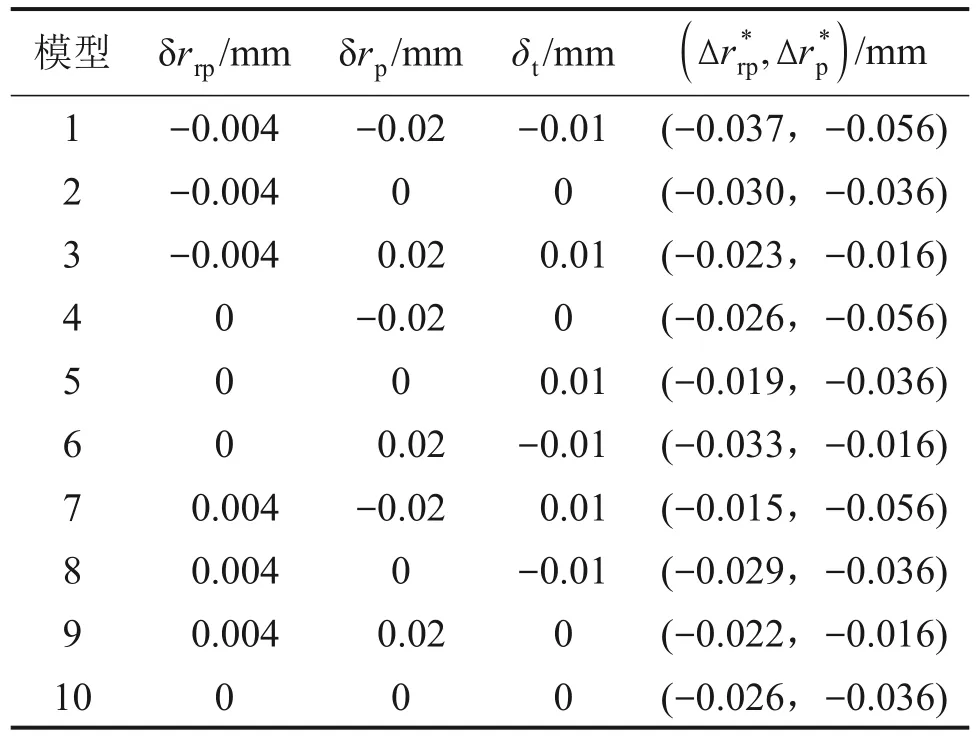
表4 正交实验方案Table 4 Orthogonal experiment scheme
3.2.1 单项误差模型计算结果分析
图11 所示为模型2、4、5 经本文修形方法得到的共轭摆线齿廓。从图11 可见:在模型2 的误差条件下,针轮和理论修形齿廓产生了过大间隙;在模型4、5 的误差条件下,针轮和理论修形齿廓发生了干涉。

图11 模型2、4、5共轭摆线齿廓Fig. 11 Tooth profiles of models 2, 4 and 5 conjugate cycloids
图12 所示为模型2、4、5 误差补偿后的摆线轮接触应力和传动误差。从图12 可见:在单项误差条件下,本文修形方法可使摆线轮最大接触应力、传动误差及其峰峰值接近于无误差模型状态,而模型2的针齿半径误差经补偿后的传动误差比模型10 的小,其原因是针齿半径减小,二次修形后摆线轮增大[22]。说明本文修形方法可以对单项误差进行较好补偿。
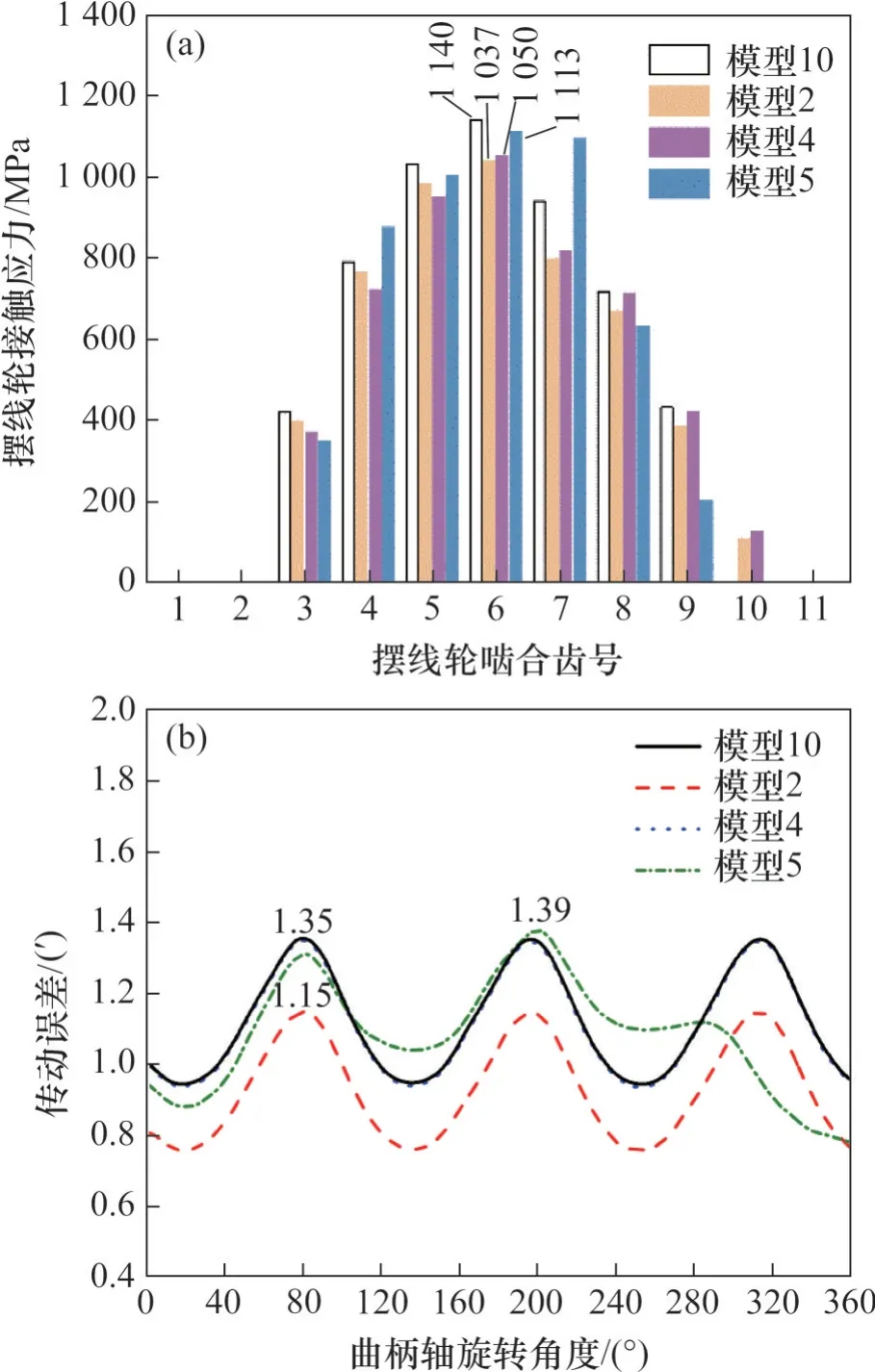
图12 模型2、4、5摆线轮接触应力分布和传动误差Fig. 12 Contact stress distribution of cycloid wheel and transmission errors in models 2, 4 and 5
3.2.2 组合误差模型计算结果分析
以模型3为例进行分析。图13所示为模型3误差补偿前后的摆线齿廓图。从图13 可见:在保证齿顶及齿根径向间隙的前提下,本文修形方法既能在齿廓工作段逼近理论零侧隙摆线齿廓满足共轭关系,又有一定的啮合侧隙,便于装拆与润滑。
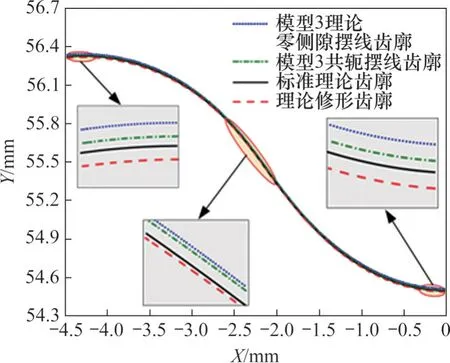
图13 模型3摆线齿廓Fig.13 Cycloid tooth profiles of model 3
图14 所示为模型3 误差补偿前后的摆线轮接触应力和传动误差。从图14 可见:误差补偿后,摆线轮最大接触应力、传动误差最大值及峰峰值都有所降低,说明本文修形方法在组合误差条件下既可以提高传动精度,也可有效改善齿面受力。

图14 模型3摆线轮接触应力分布和传动误差Fig. 14 Contact stress distribution of cycloid wheel and transmission errors in model 3
表5所示为各误差模型下理论修形方法和文中修形方法得到的传动误差和接触应力计算结果对比。从表5可以看出,现有的理论修形方法对零件加工误差的补偿能力有限(模型1、4、5及7均出现装配干涉),相比于理论修形方法,本文所提出的二次共轭修形方法在零件组合误差条件下均实现了误差补偿,可使传动误差最大值平均降低32%,传动误差峰峰值平均降低26%,摆线轮最大接触应力平均降低11%,验证了本文修形方法的正确性。

表5 正交试验结果Table 5 Orthogonal test results
4 结论
1) 本文修形方法在零件单误差及组合误差条件下均可对加工误差进行合理补偿,得到的摆线齿廓既能保证在非工作段的齿根、齿顶处留有径向间隙,又能在工作段实现摆线针轮共轭传动,满足回差精度要求。
2) 相比于理论修形方法,本文修形方法在保证传动精度的条件下,可以改善齿面受力状态,降低摆线轮最大接触应力。
3) 本文修形方法既可应用于RV减速器设计阶段,也可推广到装配阶段,以达到降低成本的目的,具有重要的工程应用价值。在RV减速器的设计阶段,通过将难加工零件尺寸的制造公差合理放大,使其按照经济精度加工,然后根据各零件尺寸的公差带,采用文中修形方法可确定摆线轮的修形量范围。在分组装配阶段,测出加工后针齿壳、针齿等零件的误差和摆线轮的实际修形量,将其各分为若干组,将不同组合的误差数据代入本文模型,确定能进行误差补偿的摆线轮修形量范围,为分组装配提供理论依据。在单件小批量生产过程中,可将摆线轮修形量作为装配尺寸链的修配环,将测量的针齿壳、针齿等零件的误差作为组成环,利用本文模型可以计算满足装配精度要求的摆线轮修形量。
