摆线针轮传动机构的偏心距对承载能力的影响

2022-06-16张跃明李连松纪姝婷

哈尔滨工程大学学报 2022年6期

张跃明，李连松，纪姝婷

(1.北京工业大学材料与制造学部，北京 100124； 2.北京智同工大智能传动技术研究院有限公司，北京 110112)

RV减速器是一种主要应用在工业机器人关节处的核心零部件，其主要优点是结构紧凑、传动比大、传动精度高、使用寿命长、振动小、能耗小等，它还广泛应用于航天航空、自动化设备、数控机床等领域[1-2]。RV减速器由两级减速系统组成，第1级为渐开线齿轮行星传动机构，第2级为摆线针轮传动机构。目前，渐开线齿轮行星传动相比摆线针轮传动的技术发展更为成熟，摆线针轮传动机构作为RV减速器最重要的组成部分，其性能优劣对整机的传动精度、承载能力等性能有着重要的影响。由于摆线轮与曲柄轴加工工艺复杂、加工精度高、检测难度大，致使我国RV减速器的发展放缓。

摆线针轮传动机构属于RV减速器中重要的组成部分，提高RV减速器整机的承载能力首先需要提高摆线针轮传动机构的承载能力。摆线针轮传动机构具有非线性接触与多齿啮合的特点。在负载情况下，摆线针轮传动机构的承载能力主要由啮合区域的接触变形与接触应力来决定。国内外相关学者对摆线针轮传动机构的承载能力进行了大量的研究。李威等[3]探究了摆线针轮传动原理并计算了摆线轮与针轮之间的接触应力。王辉等[4]运用仿真软件计算了摆线轮与针轮之间的啮合力、摩擦力及接触应力。Xu等[5-6]前后建立了RV减速器中轴承与摆线针轮传动机构的广义动力学模型，运用此模型可以计算摆线轮与针轮之间的接触区域、接触深度以及接触载荷。Huang等[7]提出了一种适用于摆线针轮传动机构接触齿对的齿面接触分析(LTCA)方法。Mirko等[8]采用了有限元仿真分析方法与应变片法对摆线轮与针轮的接触应力进行测量。Li等[9]建立了一种考虑制造误差的摆线针轮传动机构理论接触分析模型。Bizarre等[10]建立了角接触球轴承完整的非线性接触模型，评估了不同加载条件下各接触点的刚度和阻尼，对摆线针轮传动机构的载荷计算具有借鉴意义。Lin等[11]提出一种摆线齿轮减速器运动误差分析和公差设计的方法，对摆线针轮减速器进行了齿面接触分析。Li等[12]提出了一种力学计算模型和有限元分析方法，对摆线齿轮减速器进行受载接触分析。Yu等[13]针对圆柱齿轮的齿廓修形，提出了一种非赫兹柔度矩阵齿形接触分析方法，并用光弹法进行了实验验证。Sensinger等[14]探究了改变摆线轮的齿数，承载能力的变化情况。Meng等[15]探究了运动学参数对摆线针轮传动机构传动性能的影响。Hsieh等[16]建立了小齿差摆线针轮减速器的系统动力学分析模型。Tran等[17]通过有限元分析和运动学分析相结合的方法，对运转的摆线针轮减速器进行了研究。在上述的研究中，摆线针轮传动机构承载能力的评估因素比较少，单一地考虑接触应力或者接触刚度不足以准确地评估摆线针轮传动机构的承载能力。有限元仿真分析和实验验证相比理论模型计算的结果更为准确，但是，其计算效率并不高。针对以上问题，需要建立完整并准确的摆线针轮传动机构承载能力理论模型。

偏心距作为摆线针轮传动机构最重要的设计参数之一，偏心距的选取不仅决定着摆线轮齿廓曲线的齿形，并且影响着摆线针轮传动机构的承载能力与传动效率。目前，偏心距的确定往往依据经验选取，缺乏理论依据，这导致机构的承载能力很难达到最佳，针对此问题，本文以提高摆线针轮传动机构的承载能力为目标，建立准确的摆线针轮传动机构承载能力理论模型；然后，探究偏心距对承载能力的影响规律；最后，以承载能力系数最高为优化目标确定偏心距，并对其进行分析验证。

1 摆线针轮传动机构承载能力计算模型

1.1 摆线针轮传动原理

摆线轮通用的齿形方程式[18]为：

(1)

式中：e为偏心距；Rp为滚针分布圆半径；Zp为针轮齿数；Rg为滚针半径；b为摆线轮厚度；ΔRp为摆线轮移距修形量；ΔRg为摆线轮等距修形量；iH为摆线轮齿数和针轮齿数的相对传动比，iH=Zp/Zc；φ为转臂相对于某一针齿中心矢径的转角，也称为啮合相位角；k1为短幅系数，k1=eZp/(Rp+ΔRp)；S=1+k12-2k1cosφ；x为摆线轮齿廓曲线横坐标值；y为摆线轮齿廓曲线纵坐标值。

从摆线轮齿廓方程可以看出，摆线轮齿形由偏心距e、针轮齿数Zp、滚针分布圆半径Rp、滚针半径Rg所决定，因此，称其为摆线轮的基本齿形参数。但是，在实际生产应用中，为了补偿制造误差，保证良好的润滑，需要对摆线轮齿廓进行修形，其中最常用的修形方式是等距修形与移距修形的组合修形方式。

摆线针轮机构传动啮合原理图如图1所示。摆线针轮传动机构中针轮是固定不动的，xpOpyp为针轮坐标系，即为固定坐标系，坐标原点Op；xcOcyc摆线轮坐标系，转臂方向作为xc轴方向，坐标原点Oc。摆线轮绕着针轮中心公转，公转中心为Op，如图所示，公转α角度，同时摆线轮自身也在自转，自转方向与公转方向相反。

摆线针轮传动机构在运行过程中，摆线轮与多个滚针啮合，摆线轮齿廓的啮合点都存在指向节点P的啮合力F。固定坐标系下，滚针所在位置与转臂方向呈β角度，啮合力F与转臂方向呈θ角度。摆线针轮所受啮合力F与摆线轮旋转中心Oc的距离为力臂l。

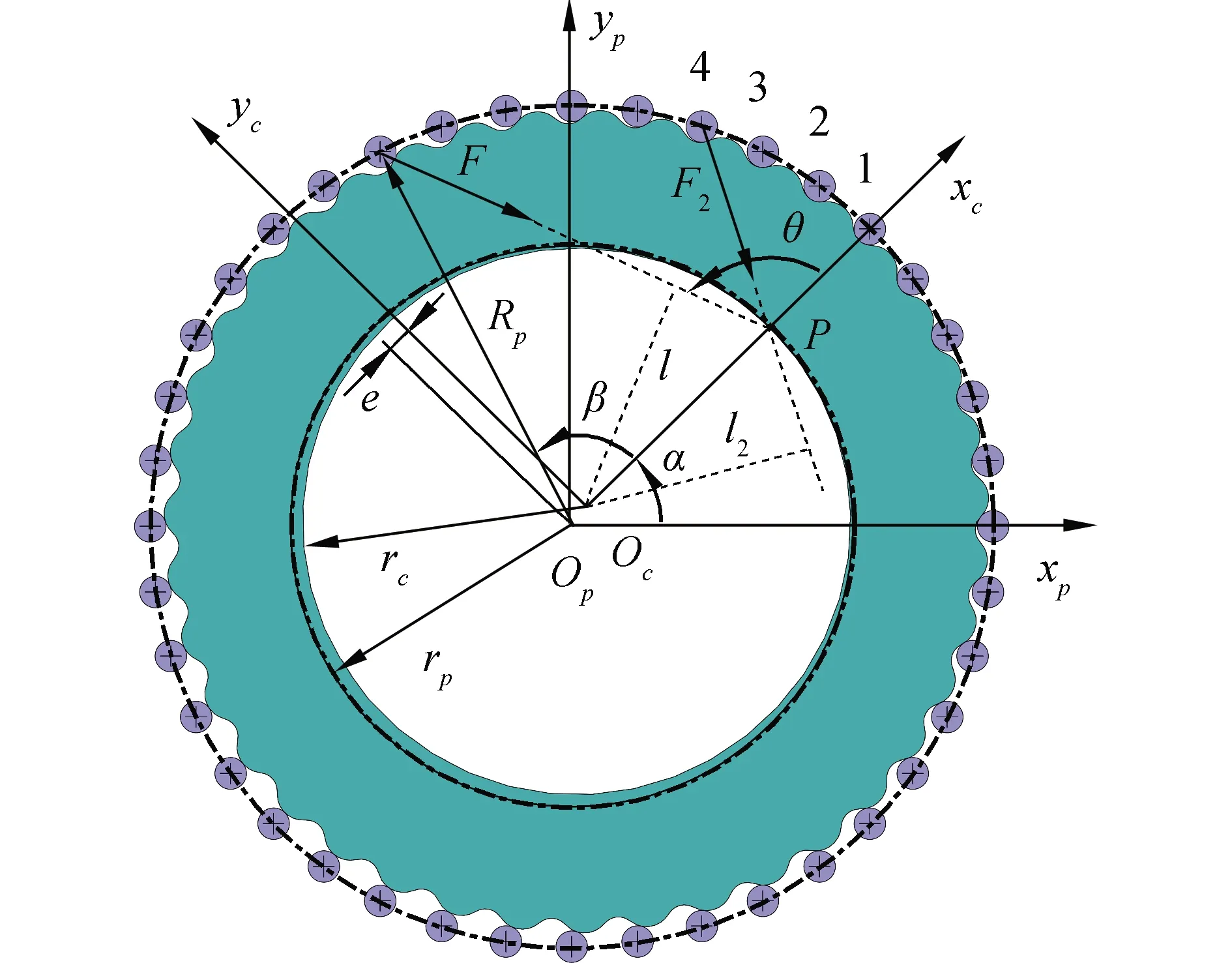
图1 摆线针轮啮合原理Fig.1 Cycloid-pin gear meshing principle

在啮合传动中，针轮坐标系下节点P的运行轨迹为针轮节圆，针轮节圆半径为rp，rp=e·Zp；摆线轮坐标系下节点P的运行轨迹为摆线轮节圆，摆线轮节圆半径为rc=e·Zc，2节圆相切于节点P。

1.2 摆线针轮传动机构接触应力计算模型

如图2所示，RV减速器中摆线针轮传动机构的滚针大多采用“卧枕式”，滚针在啮合状态下，受到的弯曲应力很小，所以弹性变形主要考虑接触变形。

图2 卧枕式滚针结构Fig.2 Horizontal pillow type needle roller structure

未修形处理的摆线轮与针轮啮合时，一半的滚针参与啮合传力。为了便于安装、拆卸并保证良好的润滑，摆线轮需要修形处理，修形处理后的摆线轮与针轮的同时啮合齿数小于一半的针轮齿数，且摆线轮齿与滚针之间会产生大小不等的初始间隙。第i对摆线轮齿与滚针沿待啮合点法线方向的初始间隙[18]为：

(2)

式中φ为转臂相对于某一针齿中心矢径的转角，也称为啮合相位角。

摆线轮齿与滚针之间的接触可以假设为圆柱与圆柱之间的接触，根据圆柱与圆柱物体之间的赫兹接触公式[19]可以得到摆线轮齿与滚针之间最大接触变形δmax与最大法向载荷Fmax的关系式：

(3)

式中：u1、u2分别为摆线轮与滚针的泊松比；E1、E2分别为摆线轮与滚针的弹性模量；ρc为摆线轮齿廓曲率半径；c为摆线针轮传动机构啮合区间的接触半宽。

接触半宽c的推导公式为：

(4)

式中：ρD为摆线针轮综合曲率半径；ED为摆线针轮等效弹性模量。

摆线轮实际齿廓曲率半径ρc[18]为：

(5)

已知，当摆线轮齿廓曲线曲率ρc为正值，曲线向内凹；当ρc为负值，曲线向外凸。

综合曲率半径ρD为：

(6)

摆线轮等效弹性模量ED为：

(7)

由于接触变形，摆线轮会转过一个角度φ，如图3所示。第i对摆线轮齿与滚针啮合所产生的接触变形量δi与啮合力的力臂li满足δi=φ·li。由此可知，摆线针轮传动机构接触变形量之比等于力臂之比，表达式为：

(8)

式中：lmax为摆线针轮啮合点最大的力臂；δmax为摆线轮齿与滚针之间的最大接触变形量。

当摆线针轮传动机构中摆线轮齿廓所受啮合力方向与转臂方向垂直时，啮合力的力臂取到最大值，此刻，最大力臂与摆线轮节圆半径相等，即lmax=rc。力臂计算公式为：

(9)

根据式(8)、(9)可以得到每一个齿的接触变形量：

(10)

设摆线针轮传动机构中第i对摆线轮齿与滚针啮合所产生的实际接触变形量为Δi，Δi=δi-Δdi，Δi可以判断该机构中第i对摆线轮齿与滚针是否参与啮合传力，当Δi>0时，参与啮合传力；当Δi=0时，处于临界状态(即将进入啮合或即将退出啮合)；当Δi<0时，不参与啮合传力。由此即可确定负载情况下同时啮合齿数，进而确定其啮合区间。如图4所示，根据接触变形量与初始间隙曲线图可以计算出啮合齿数为9个。

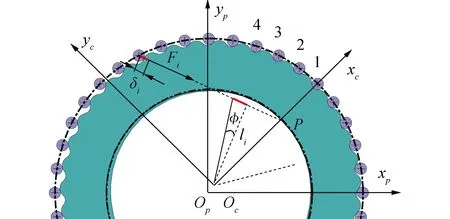
图3 接触变形量与力臂关系Fig.3 Relationship between contact deformation and force arm

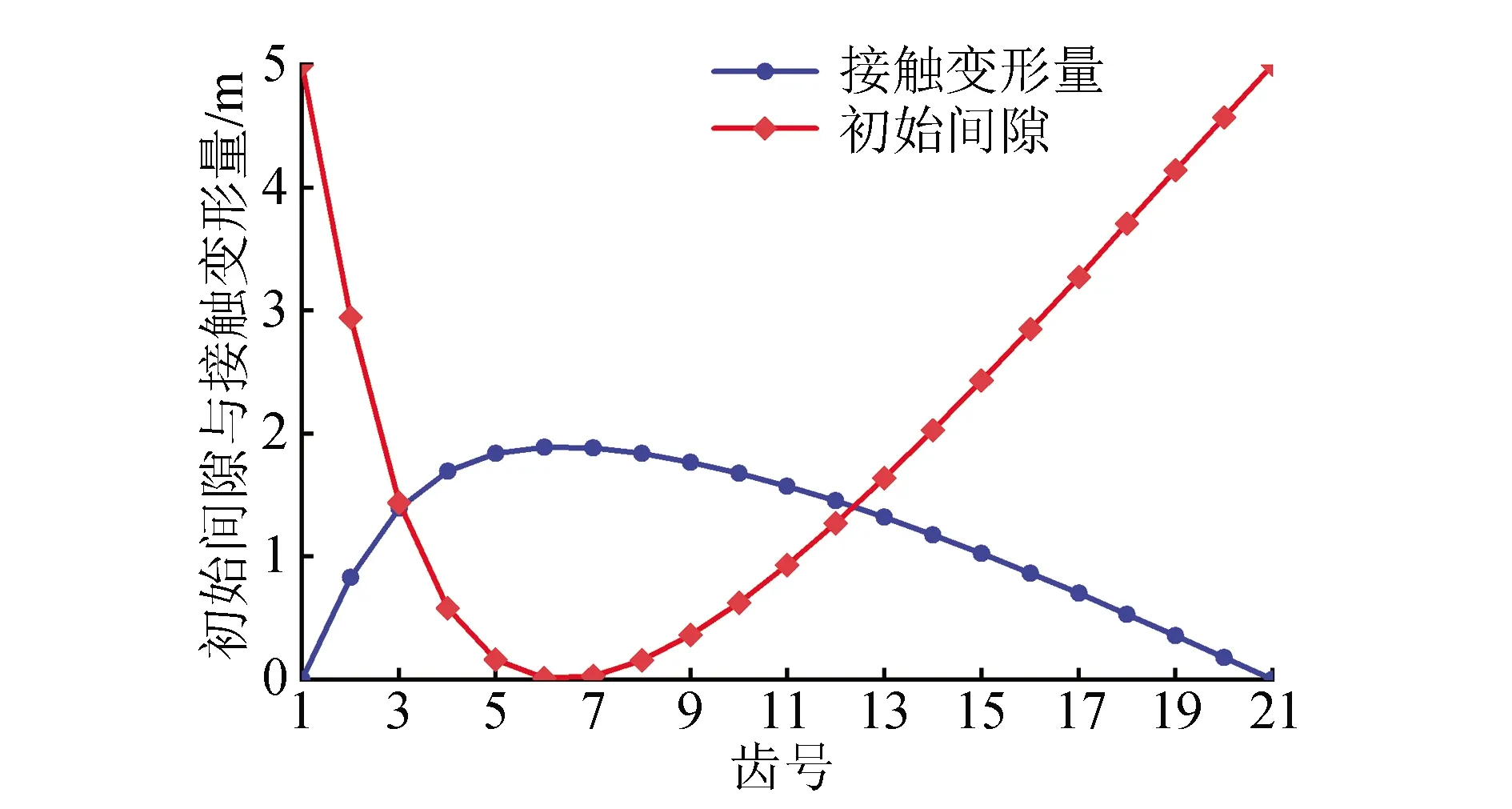
图4 初始间隙与接触变形量随齿号的变化Fig.4 Variation of initial clearance and contact deformation with tooth number

由赫兹计算公式可知，摆线针轮传动机构中第i对摆线轮齿与滚针之间的啮合力Fi与最大初始啮合力Fmax之比等于第i对啮合齿实际接触变形量δi-Δdi与最大接触变形量δmax之比。摆线针轮中第i对啮合齿的啮合力Fi：

(11)

由于初始间隙的存在，摆线轮只与部分滚针接触，假设只有滚针号m到滚针号n啮合接触，根据转矩平衡原理，可得：

(12)

最先接触点处的啮合力Fmax0为：

(13)

由于，若求解实际摆线针轮传动机构的最大接触变形量时，需要最大初始啮合力值Fmax作为已知值，暂取标准摆线轮与针轮之间的最大啮合力作为最大初始啮合力Fmax。由式(11)～(13)可知，无修形处理的标准齿形摆线轮与针轮啮合的最大啮合力求解公式为：

(14)

式中：Tc为单个摆线轮传递的扭矩；T为输出轴传递的总转矩。由于制造误差，Tc略大于0.5T，Tc=0.55T。

因为，求解实际摆线针轮传动机构的最大接触变形量δmax时，将标准齿形摆线轮与针轮之间的最大啮合力作为最大初始啮合力Fmax，所以，求解得到的Fmax0与最大初始啮合力Fmax存在差距，需采用迭代算法求解精确最大初始啮合力Fmax。首先，判断是否满足条件∣Fmax-Fmax0∣≤0.1%Fmax，如果不满足条件，则将Fmax0的值赋予Fmax，代入式(3)重新进行计算，直到满足条件，此刻，Fmax=Fmax0，模型计算流程图如图5所示。

根据精确的最大初始啮合力Fmax可求解得到摆线轮与针轮之间的各齿啮合力，以及摆线轮齿廓上啮合力F的分布，再根据赫兹接触公式[19]可以求解得到摆线轮齿廓上接触应力σH的分布。

摆线轮与针轮之间的接触应力计算公式为：

(15)

以RV-20E减速器中摆线针轮为例，使用Matlab数学工具，首先，输入其设计参数、材料参数、修形参数等，参数设置如表1所示；然后，根据上述计算模型编程计算；最后，得到摆线轮齿廓上啮合力与接触应力随转臂旋转0°～180°的分布曲线和最大接触应力σHmax，如图6所示。

1.3 摆线针轮传动机构接触刚度计算模型

摆线轮齿与滚针理论情况下是线接触，实际啮合会有弹性变形。摆线轮齿与滚针接触近似可以看成圆柱与圆柱啮合，如图7所示。根据圆柱与圆柱物体之间的赫兹接触公式[19]可以得到摆线轮与滚针啮合时，摆线轮的接触变形量δc与滚针的接触变形量δg为：

(16)

(17)

表1 摆线针轮传动机构基本参数

摆线针轮传动机构中摆线轮齿与滚针啮合点处的接触刚度计算公式为：

(18)

(19)

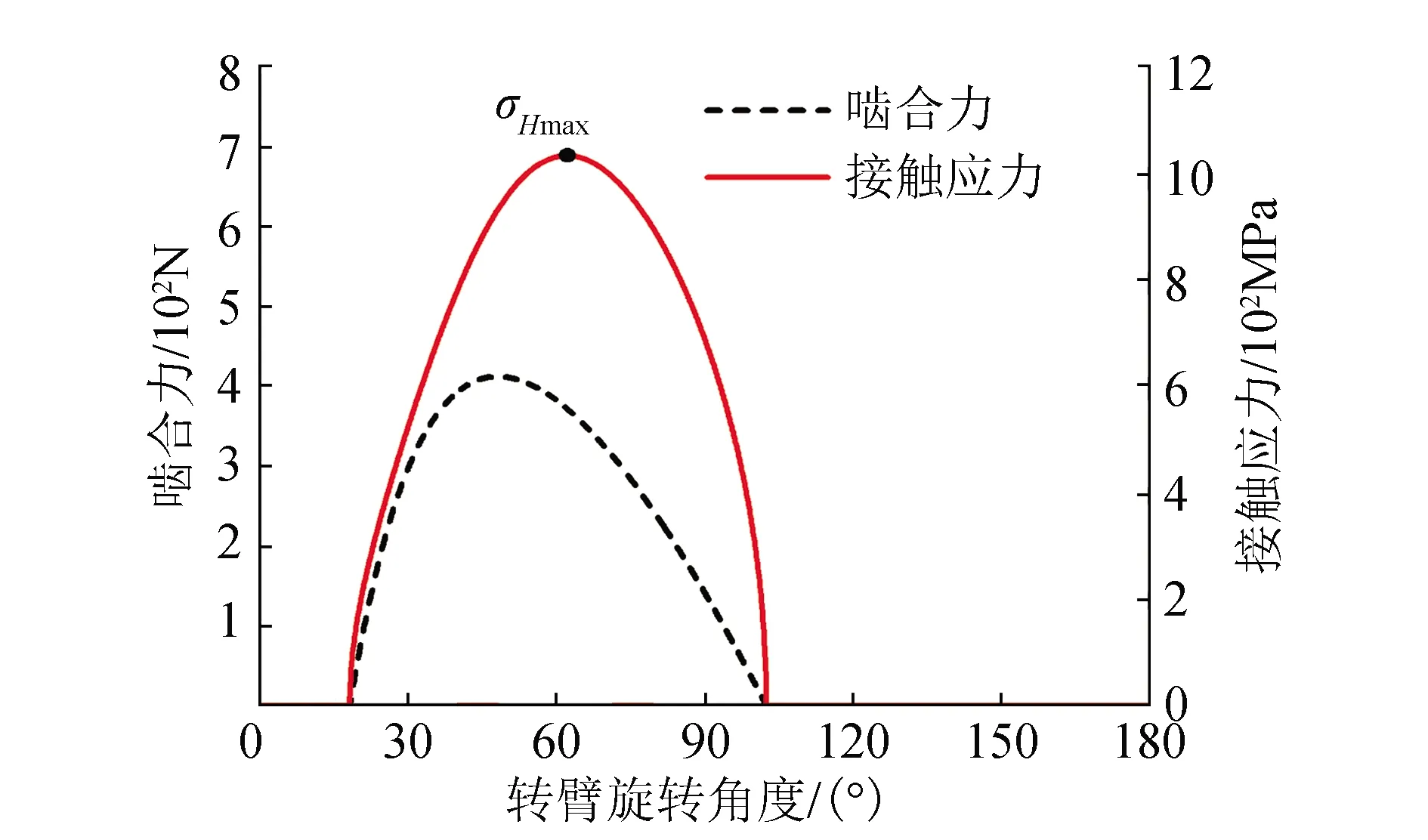
图6 齿廓上啮合力及接触应力随转臂旋转角度的变化Fig.6 Variation of meshing force and contact stress on tooth profile with rotation angle of rotating arm

图7 摆线针轮接触变形Fig.7 Contact deformation of cycloid-pin gear

由于摆线轮齿与滚针啮合时单齿的综合接触刚度属于摆线轮接触刚度与滚针接触刚度的串联，如图8所示，摆线针轮传动机构的单齿接触刚度K为：

(20)

根据对式(20)简化可知，摆线针轮接触刚度与其啮合力、机构参数、材料参数等有关。通过在Matlab数学工具编程计算，可以得到齿廓接触刚度K的分布曲线，最大接触刚度为Kmax，如图9所示。

图8 单摆线轮齿与滚针接触Fig.8 Contact between single cycloid gear tooth and pin roller

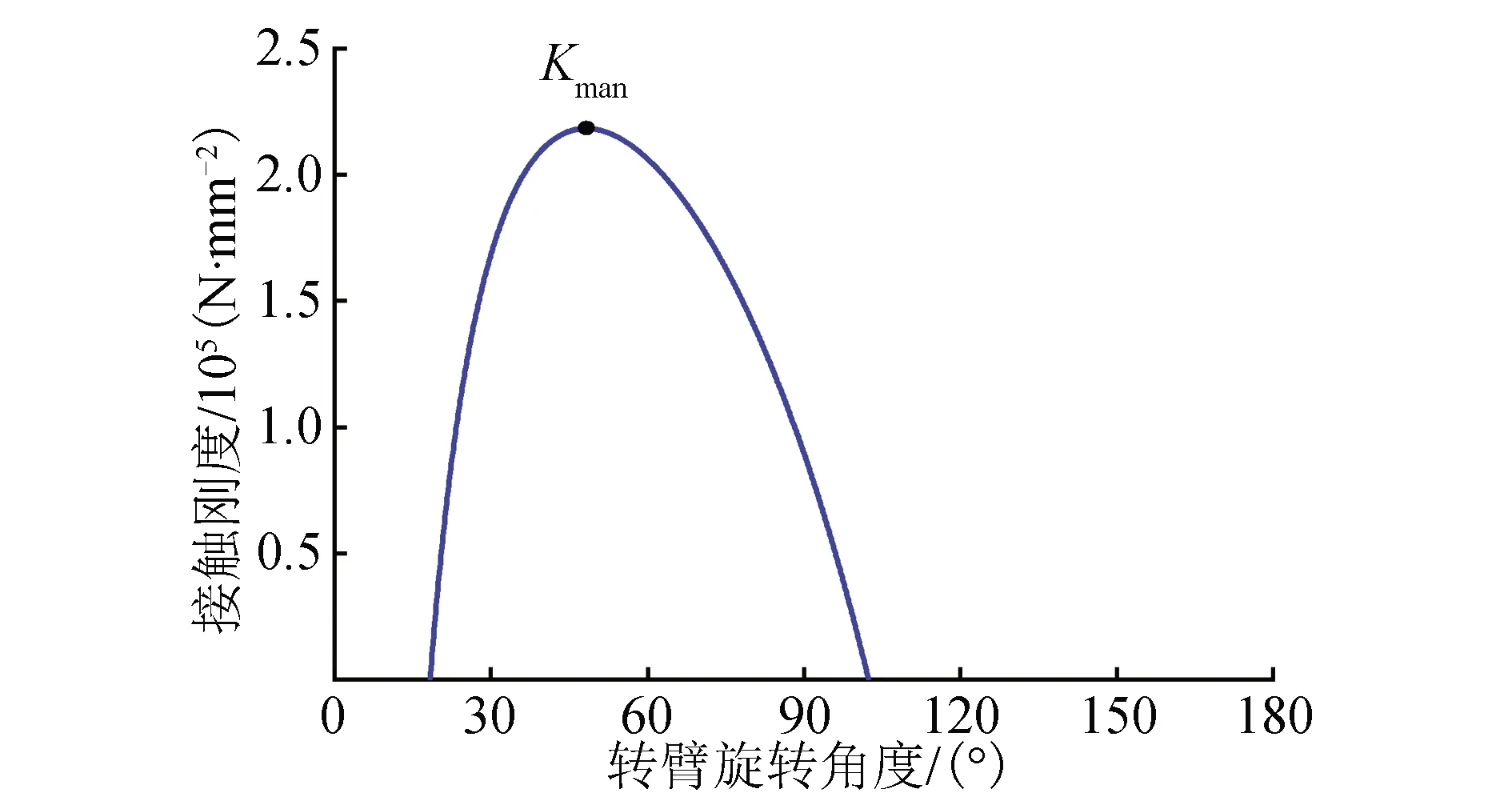
图9 齿廓上接触刚度随转臂旋转角度的变化Fig.9 Variation of contact stiffness on tooth profile with rotation angle of rotating arm

1.4 摆线针轮传动机构承载能力系数计算模型

在计算渐开线齿轮、轴承等传动部件的承载能力时主要以机构啮合区域的最大接触应力作为评价标准。为了更加准确地评价摆线针轮传动机构的承载能力，本文引入了摆线针轮传动机构承载能力系数C，承载能力系数C综合了摆线轮与针轮之间的最大接触应力σHmax与最大接触刚度Kmax。

已知摆线针轮传动机构啮合区域的最大接触应力越小、最大接触刚度越大，即承载能力系数越大，表示该机构承载能力越高。摆线针轮传动机构承载能力系数C：

(21)

式中：Kmax0为标准偏心距的摆线针轮传动机构的最大接触刚度，Kmax0=2.181 5×105N/mm；σHmax0为标准偏心距的摆线针轮传动机构的最大接触应力，σHmax0=1 033.386 9 MPa。

2 摆线针轮传动机构的偏心距对承载能力的影响

已知偏心距e、滚针分布圆半径Rp、针轮齿数Zp、滚针半径Rg、摆线轮厚度b是摆线针轮传动机构最重要的5个设计参数。摆线针轮传动机构的承载能力属于整机综合性能的指标之一。探究摆线针轮传动机构设计参数对其承载能力的影响有助于优化摆线针轮的结构并提高RV减速器整机的运动精度、寿命及传动效率。

基于摆线针轮传动机构承载能力计算模型，本节主要探究了偏心距e对该机构承载能力的影响。首先，探究偏心距e对摆线轮与针轮之间的最大接触应力的影响；然后，探究偏心距e对摆线轮与针轮之间的最大接触刚度的影响；最后，探究偏心距e对摆线针轮传动机构承载能力系数的影响，并以承载能力系数最高来确定最佳偏心距。

2.1 偏心距对最大接触应力σHmax的影响

首先，在Matlab软件中编写摆线针轮传动机构承载能力计算程序；然后，将原始摆线针轮传动机构设计参数与摆线轮齿廓修形量代入编写的Matlab程序中；最后，以0.001 mm为一间隔，在0.8～1.2 mm范围内改变偏心距e的值，探究摆线轮与针轮之间最大接触应力的变化趋势。如图10所示。

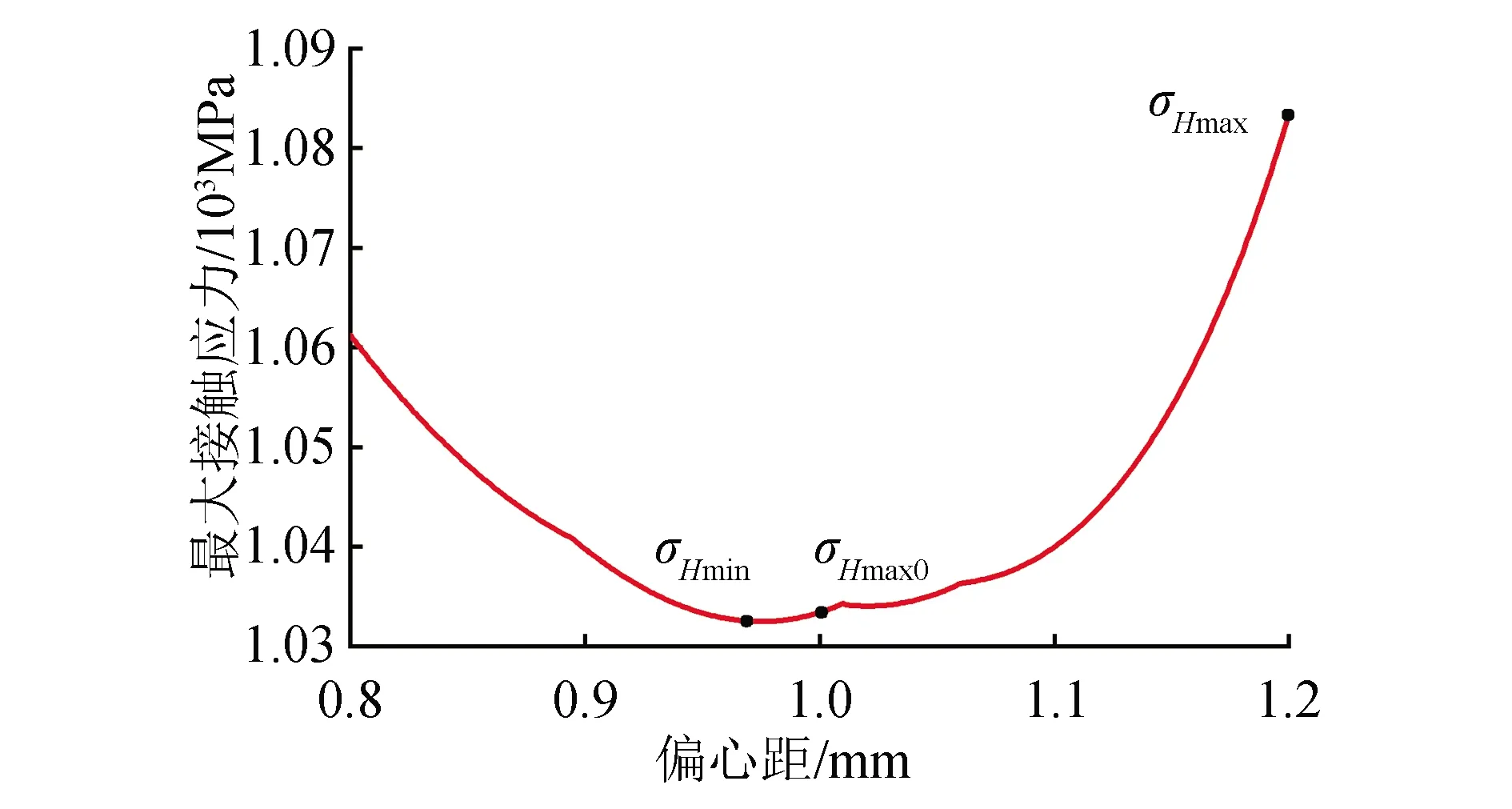
图10 最大接触应力随偏心距的变化趋势Fig.10 Variation trend of maximum contact stress with eccentricity

通过图10观察得到，随着偏心距的增加，摆线针轮传动机构中摆线轮与针轮之间的最大接触应力有先减小再增加的趋势。当偏心距为0.975 mm时，摆线轮与针轮之间的最大接触应力取得最小值，σHmin=1 032.479 0 MPa；当偏心距为1.2 mm时，最大接触应力取到最大值，σHmax=1 083.554 5 MPa，最大接触应力最大值与最小值差值为51.075 5 MPa。偏心距为1 mm的情况下，摆线针轮传动机构的最大接触应力为1 033.386 9 MPa。当偏心距为0.975 mm的最大接触应力取得最小值，此时，摆线针轮传动机构的承载能力会相应提高。

2.2 偏心距对最大接触刚度Kmax的影响

探究偏心距对摆线轮与针轮之间的最大接触刚度的影响方法与探究偏心距对最大接触应力的影响方法类似，在此不再赘述。通过Matlab软件编程计算，得到摆线针轮传动机构最大接触刚度随着偏心距的增加而变化的趋势，如图11所示。

图11 最大接触刚度随偏心距的变化趋势Fig.11 Variation trend of maximum contact stiffness with eccentricity

如图11所示，观察得到，随着偏心距e的增加，摆线轮与针轮之间最大接触刚度先减小再增加，当偏心距为0.943 mm时，最大接触刚度取得最小值，Kmin=2.182 68×105N/mm；当偏心距为1.2 mm时，最大接触刚度取到最大值，Kmax=2.200 58×105N/mm，摆线针轮传动机构最大接触刚度最大值与最小值的差值为1 790 N/mm。

接触刚度的定义是零件结合面在外力作用下，抵抗接触变形的能力，所以，有效提高摆线针轮传动机构的接触刚度可以提高该机构的承载能力。

2.3 偏心距对承载能力系数C的影响

通过在Matlab软件中编程计算，可以得到摆线针轮传动机构承载能力系数C随着偏心距的增加而变化的趋势，如图12所示。

图12 承载能力系数随偏心距的变化趋势Fig.12 Variation trend of bearing capacity coefficient with eccentricity

如图12所示，e1=0.959 mm，e2=1 mm。已知标准偏心距的摆线针轮传动机构承载能力系数C0为0，偏心距e1～e2范围内的摆线针轮传动机构承载能力系数大于0，表明机构的承载能力更大。

当偏心距值为0.98 mm时，承载能力系数C达到最大值，最大值为Cmax，Cmax=5.008 59×10-4。此时，摆线针轮传动机构有最好的承载性能，因此，将0.98 mm作为最优偏心距值代入后续计算中。

3 摆线针轮传动机构有限元仿真分析

本机主要运用ANSYS Workbench有限元仿真分析软件计算摆线针轮传动机构的接触应力，验证承载能力理论计算模型的准确性。

首先，根据摆线针轮传动机构的基本参数建立分析模型；然后，运用ANSYS Workbench有限元仿真分析软件计算摆线轮与针轮之间的接触应力并找到最大接触应力值；最后，将摆线针轮传动机构理论计算模型计算的各齿接触应力与有限元仿真分析软件计算的各齿接触应力进行对比分析，做出对比分析曲线图。

3.1 摆线针轮传动机构模型建立

运用Matlab软件编写摆线轮齿廓方程，即式(1)代入表1中摆线轮齿形参数并运行，得到摆线轮齿廓曲线，然后将偏心距的值改为0.98 mm，重新得到新的摆线轮齿廓曲线。

在SolidWorks软件中导入摆线轮齿廓曲线，再根据摆线针轮传动机构基本参数建立摆线针轮传动机构三维模型。仿真分析主要计算摆线轮齿与滚针接触区域的接触应力及应力分布，为了简化计算过程，提高计算效率，将所有滚针与针齿壳作为一体，摆线针轮传动机构简化为2个零件。

3.2 有限元仿真分析

首先，将SolidWorks中的摆线针轮传动机构三维模型导入ANSYS Workbench有限元仿真分析软件Static Structural模块中；然后，在Design Modeler中分别设置材料类型、分析类型、坐标系、接触类型、网格划分、施加约束、施加载荷、设置解决方案等；最后，对其进行运行求解，观察摆线针轮传动机构接触应力的分布。

为了提高模型的仿真计算效率，根据机构的特点采用2D平面分析类型。前处理过程中，此模型的网格划分属于难点，首先，摆线轮与针轮按照3 mm三角形网格划分，然后，摆线轮齿面与针齿面再次按照1 mm进行划分，最后，为了使啮合点处的仿真数值更为准确，故每一个啮合点的网格还需要细化，当啮合点1 mm半径范围内的网格细化到0.01 mm时，就可以清晰地观察到应力分布了，此时，网格划分单元数为84万左右，节点数是169万左右。网格划分情况如图13所示。

图13 网格划分Fig.13 Grid generation

在e=1 mm的摆线针轮传动机构与e=0.98 mm的摆线针轮传动机构都施加92.95 N·m逆时针的旋转扭矩，得到接触应力分布图，如图14与图15所示。如图显示偏心距为1 mm的摆线针轮传动机构由于摆线轮修形，第4～10对轮齿参与啮合，在第8对轮齿处出现最大接触应力，应力值为962.06 MPa。仿真分析结果与理论计算的误差率为6.90%。偏心距为0.98 mm的摆线针轮传动机构第4～10对轮齿参与啮合，最大接触应力为938.03 MPa，仿真分析结果与理论计算的误差率为9.15%。由于计算误差较小，表示有限元仿真验证了理论计算的准确性。

图14 摆线针轮传动机构接触应力分布Fig.14 Contact stress distribution of cycloid-pin gear transmission mechanism

3.3 仿真曲线分析

为更好体现摆线针轮传动机构理论模型计算与ANSYS Workbench有限元仿真分析的对比性，首先，通过Matlab数学软件计算并得到偏心距分别为1 mm与0.98 mm的摆线针轮传动机构的接触应力分布；然后，再通过ANSYS Workbench有限元仿真分析软件计算并得到两摆线针轮传动机构的接触应力分布；最后，根据计算得到的数据结果做接触应力对比分析曲线图，如图16所示。

根据图16观察可知，2种不同偏心距下有限元仿真分析与理论计算得到的摆线针轮最大接触应力误差率都在允许范围之内，验证了理论模型计算的准确性；理论计算得到的摆线轮与针轮的同时啮合对数比有限元仿真计算得到的同时啮合对数少2对；有限元方法验证了最优偏心距比标准偏心距的摆线针轮最大接触应力降低了2.8%；2种计算方法的结果都显示出0.98 mm偏心距的摆线针轮传动机构最大接触应力比1 mm偏心距的最大接触应力有所降低，证明了偏心距e的选取采用承载能力系数C最高的方法是可行的。