预期寿命对中国家户储蓄和健康投资行为的影响*

俞秀梅 雷晓燕 王 敏

一、引言

自十一届三中全会以来，我国经济持续高速增长。经济水平的提高大幅度提升了我国居民的健康水平，人均预期寿命从1981 年的67.77 岁增长到2015 年的76.34 岁。①数据来源:《中国统计年鉴2021》。然而，正如我国政府在2016 年10 月发布的《健康中国2030 规划纲要》指出，在当前形势下，“工业化、城镇化、人口老龄化、疾病谱变化、生态环境及生活方式变化等，也给维护和促进健康带来一系列新的挑战，健康服务供给总体不足与需求不断增长之间的矛盾依然突出，健康领域发展与经济社会发展的协调性有待增强”。该纲要首次在中央政府层面提出“把健康摆在优先发展的战略地位”。可以预计，随着该纲要的落地实施以及经济的进一步增长，我国居民的预期寿命还将继续提升。预期寿命和健康水平的变化不但直接关系到居民福利，也影响每个家庭的经济活动和决策。因此，当我国政府提出要将健康发展上升为国家发展战略时，一个重要的研究问题是，以预期寿命为代表的公共健康水平的提升对我国经济社会的长期发展会产生什么样的影响。

预期寿命是公共健康水平的一般性衡量指标。在早期的经济增长文献中，大量的跨国实证研究把预期寿命作为增长回归模型的一个重要解释变量，发现一国发展初期的预期寿命水平对其未来长期经济增长有显著的正向影响(Barro 和Lee，1994；Barro 和Sala-I-Martin，1995；Barro，1996；Hamoudi 和Sachs，1999；Bhargava 等，2001；Bloom 等，2004)，而且初始期的高预期寿命对发展中国家增长绩效的正向影响尤为显著(Kelley 和Schmidt，1995；Sachs 和Warner，1997；Zhang 等，2003)。这些实证研究虽然发现了初始预期寿命与长期经济增长的因果关系，但对于其背后的理论机制并不清楚(Temple，1999)，直到Chakraborty (2004)从储蓄和投资的角度提供了理论解释和微观基础。Chakraborty (2004)通过构建两期世代交替模型(overlapping generations model，OLG)，将预期寿命设定为政府公共医疗支出的递增函数以及人们对未来效用的贴现因子。在该模型中，当一个经济体初始预期寿命较高，人们就会积极增加储蓄以提升未来老年时期的消费和效用水平。由于在均衡条件下储蓄等于资本投资，高预期寿命最终会通过资本投资这个渠道带动未来收入水平的增长。收入的增长则会进一步增加政府财税收入以及公共健康支出，从而促进预期寿命的进一步提升。由于预期寿命和经济增长之间存在这样一个互相加强的效应，当某一经济体初始预期寿命较低时，该经济体在长期就有可能陷入低收入、低预期寿命的贫困陷阱。反之，该经济体则步入高收入、高预期寿命的稳态均衡。Zhang 和Zhang (2005)进一步利用三期世代交替模型(OLG)证明，虽然预期寿命上升会增加家庭储蓄率，但是由于消费边际效用递减以及生产要素边际产出递减，预期寿命增加对储蓄率的正向影响是递减的。

所有的宏观经济活动都是微观经济行为的加总。显然，要了解预期寿命对经济社会长期发展的影响，探究预期寿命对微观家户经济决策和行为的影响至关重要。在Chakraborty (2004)的基础上，本文基于两期世代交替模型分析了预期寿命对家户储蓄和健康投资的双重影响，并利用2004—2009 年我国城镇住户调查数据以及全国疾病监测系统死因监测数据库提供的疾病死亡率数据，对理论模型所推导出来的假说进行实证检验。在本文的两期世代交替模型中，人们在年轻时期工作获得收入，并将收入用于商品消费、储蓄和健康投资；到了老年时期，人们退休并依靠年轻时期的储蓄生活。其中，老年人的寿命有一定的时限，而人们在年轻时期的健康投资支出则可以增加未来老年时期的预期寿命。正如1993 年世界银行发布的《世界发展报告:投资于健康》所提到的，“个人对自己健康所能做的要比政府多得多”。因此，要全面考量预期寿命对家庭经济决策和行为的影响，家庭储蓄和健康投资都是不可或缺的变量。①Bhattacharya 和Qiao (2007)就曾发现，如果在Chakraborty (2004)的模型中考虑个人健康投资对预期寿命的影响，一国的经济就会产生内生的周期性波动。而后两者本质上分别对应着物质资本投资和人力资本投资，是实现长期经济增长的两个重要引擎。

本文的理论模型表明，预期寿命在通过改变贴现因子直接影响年轻人储蓄的同时，也会直接影响他们的健康投资。尤其是当人们预期到未来老年时期的寿命水平较低时，他们有更强的激励在年轻时期增加健康投资。考虑到健康投资支出的增加会挤占储蓄，预期寿命对储蓄率的影响事实上存在直接(改变贴现因子)和间接(健康投资挤占)两种效应，而且这两种效应的方向是一致的。在实证研究部分，本文先运用全国疾病监测系统死因监测数据库中的死亡率数据，基于简略生命表方法计算各城市的预期寿命水平；然后在城镇住户调查数据中匹配这些城市户主年龄在25—60 岁之间的家户样本，并在控制家户和城市经济特征变量、时间和城市固定效应的基础上，回归分析当地城市人口60岁时的预期寿命对这些家户的储蓄率以及健康投资支出的影响，即未来老年时期的预期寿命对年轻家户当前经济决策的影响。回归结果表明，预期寿命的提升在显著增加家户储蓄的同时，显著减少了家户的健康投资支出——这与理论模型预测相一致。

在现有的国内外文献中，尚没有研究讨论过预期寿命对家户健康投资支出的影响。本文在这方面做了初步的尝试，为有关预期寿命对家户经济决策和行为影响的研究提供重要补充。而在有关预期寿命对储蓄率影响的实证研究中，大部分是利用跨国数据进行分析(Bloom 等，2003；Zhang 和Zhang，2005；Bloom 等，2007；Li 等，2007)。在这些跨国研究中，由于数据可得性问题，被解释变量往往包含了居民、企业和政府三者加总的国民总和储蓄率，即总储蓄占GDP 的比重，而不是居民家户储蓄率。其中，Zhang 和Zhang (2005)则是利用投资占GDP 的比重来近似替代储蓄率。这些研究大多支持预期寿命增加对储蓄率有正向影响的结论。①其中，Zhang 和Zhang (2005)采用76 个国家1960—1989 年的数据发现，预期寿命增加会导致储蓄率增加，但是效果随着预期寿命的增加而递减。Bloom 等(2007)考虑了内生退休时间问题，利用跨国数据证明预期寿命对储蓄率的影响与养老保险的安排有关:当养老保险覆盖较全面、延迟退休激励很小时，预期寿命会对储蓄率有正影响，否则影响不显著。在国内的相关研究中，范叙春和朱保华(2012)、汪伟和艾春荣(2015)均利用省级面板数据，证实预期寿命增加提高了我国的国民总和储蓄率。刘生龙等(2012)、章元和王驹飞(2019)则是少有的关注预期寿命对我国家户储蓄率影响的研究。其中，刘生龙等(2012)基于我国1990—2009 年省级面板数据发现，预期寿命每增长1 岁会导致我国城乡居民储蓄率上升1.2 个百分点；而基于2005—2013 年地级市面板数据，章元和王驹飞(2019)则发现，预期寿命每增长1 岁会导致我国城镇家户储蓄率上升3.7 个百分点。②除利用地级市数据进行分析外，章元和王驹飞(2019)也利用微观家户数据来研究生命负担率对家户储蓄率的影响，其中生命负担率由预期寿命、户主年龄和退休年龄三个变量共同计算得出，因此分析结论也间接包含了预期寿命对家户储蓄率的影响。

与上述这些实证研究不同的是，本文主要基于城市层面的预期寿命数据以及微观家户调查数据展开分析讨论，在以下几个方面弥补了现有研究的不足:第一，现有实证研究多采用国家或者省级层面的预期寿命变量。无论是家户储蓄还是健康投资都是人们基于对未来预期寿命的感知所进行的经济决策，而人们对预期寿命的感知恰恰来自其对生活所在地人群(尤其是老年人群)死亡率的观察。一个国家或一个省份内部不同地区发展程度以及预期寿命差异较大，但在有限的生活半径内，人们难以形成这种宏观层面的预期寿命水平的认知。相比之下，基于日常的社交网络，人们可以相对容易地感知或观察到其生活所在城市老年人群的死亡率。因此，采用城市一级的预期寿命数据能够较好地反映人们对自身未来预期寿命的实际感知。第二，现有实证研究都是采用地区预期寿命水平对该地区所有年龄人口的总储蓄率进行回归，无法体现人们基于对未来寿命的预期进行当下经济决策的理论逻辑。一个人的生命周期中主要在工作期间进行储蓄。因此，要验证理论推导，正确的实证策略是看未来退休时点的预期寿命水平对工作年龄人口储蓄率的影响。本文的实证回归分析的恰恰是一座城市的人口在60 岁时的预期寿命对该城市25—60 岁工作人群储蓄率的影响，符合理论模型设定。第三，宏观层面的预期寿命水平和储蓄率均受到当地经济发展水平的影响。因此，基于国家或省份一级数据进行回归分析存在一定的内生性问题。相比之下，微观家户在做各种经济决策时，所在城市预期寿命水平是相对比较外生的变量。此外，我们也利用城市湿度数据作为城市预期寿命的工具变量，进一步解决可能存在的内生性问题。

最后，本文也对我国储蓄率问题的研究有一定贡献。目前中国储蓄率远高于全球平均水平，是世界上储蓄率较高的国家之一。近年来中国国民总储蓄占GDP 比重更是达到了50%的高水平，而世界平均水平只有20%左右。中国资本形成总额虽然也处于较高水平，但是1994 年以后，资本形成总额长期低于总储蓄，导致经常项目顺差，加剧了中国与其他国家的贸易摩擦。在这样的背景下，中国的储蓄问题备受关注。学者们从多个角度来解释中国居高不下的居民储蓄率问题。基于生命周期理论，Kraay(2000)、Modigliani和Cao (2004)、Horioka 和Wan(2007)以及Ang(2009)等主要讨论分析了收入增长率以及人口抚养比对我国居民储蓄率的影响。宋铮(1999)、Meng(2003)、施建淮和朱海婷(2004)、Giles 和Yoo(2007)以及Chamo 等(2013)则主要从预防性储蓄的角度讨论分析未来收入不确定对当前储蓄的影响。也有学者从文化和消费习惯(Horioka 和Wan，2007)、性别比失衡(Wei 和Zhang，2011)等其他角度解释中国高居民储蓄率现象。考虑到预期寿命是衡量人力(健康)资本的重要变量，且对家户决策影响甚大，本文利用微观家户数据从预期寿命角度解释中国居民高储蓄率现象，对现有文献进行了重要补充。

二、理论模型

为了研究预期寿命对家户消费和储蓄行为的影响，我们考虑一个局部均衡的两期世代交替模型，即对家户而言，工资和利率价格外生给定。经济体中每个人的生命周期分为年轻时期和老年时期两个阶段。每个人拥有1 单位无弹性的劳动力，并在年轻的时候工作，年老的时候退休。考虑Bhattacharya 和Qiao(2007)的模型设定，我们假设人们在老年时期有θ∈(0，1]的存活时间，即θ代表了个人的预期寿命水平。人们在年轻的时候可以通过个人的健康投资xt影响未来预期寿命水平。参考Chakraborty (2004)对预期寿命函数的设定，我们假设θ具有如下函数形式:

其中，γ和ω为外生参数，满足γ＞0，0＜ω＜1；δ是个人不做任何健康投资时所能达到的预期寿命水平，取决于当地政府的公共健康投入，且由当地的经济发展程度、卫生状况、公共医疗支出、自然环境等因素决定，对于家户而言是外生的。δ可视作人们在年轻时期所能观察到的当地人群的平均预期寿命水平，并基于此作进一步的个人健康投资xt。

该预期寿命函数满足以下特征。第一，θδ＞0，θx＞0:个人的预期寿命随当地预期寿命水平(或者说公共健康水平)增加而增加，同时也随个人的健康投资支出的增加而增加。第二，θxx＜0:随着个人健康投资支出的增加，其对预期寿命的影响是递减的，相当于健康投资的边际收益递减。第三，θxδ＜0:当地平均预期寿命水平越高，个人预期寿命提高的空间就越小，个人健康投资的边际收益越小。第四，0＜θ＜1:第二期的预期寿命在0 到1 之间。

为了清楚地展现预期寿命对家庭决策的影响机制，我们先考虑人们只对第二期消费有效用、对第一期消费没效用的较为简化的模型设定。该设定避免了消费的跨期选择问题，可以简洁明了地考察家庭资源在储蓄与健康投资之间的分配。在此基础上，我们再进一步放松这一假设，考虑人们对两期的消费均有效用的模型设定。

(一)只考虑第二期效用的模型设定

当人们对第一期的消费没有效用，年轻时期的工资收入全部用于储蓄和健康投资。此时，人们效用最大化问题如下:

其中，st为年轻时期的储蓄，为老年时期的消费，w为工资价格，R为利率价格。个人最优决策的一阶条件满足:

在这个简单模型中，年轻人只需要考虑如何将工资收入在储蓄和健康投资支出中进行最优分配:储蓄可以增加未来消费水平，健康投资可以提高未来寿命——两者都会提升未来老年时期的效用水平。式(5)表明最优的储蓄和健康支出决策要求两者在边际上带来的未来效用的增加是等价的，即储蓄的边际效用等于个人健康投资支出的边际效用。

为了考察一个地区平均预期寿命或者公共健康投入δ对个体家庭决策的影响，我们在式(5)基础上应用隐函数定理可得:

定理1 表明，个人储蓄水平随当地平均预期寿命的上升而上升，个人健康投资支出则随当地平均预期寿命的上升而下降。当人们在年轻时期发现当地平均预期寿命水平较高时，一方面会意识到进一步增加个人健康投资所带来的边际预期寿命的提升较低(θxδ＜0)，另一方面则会意识到未来寿命较长、增加个人储蓄的边际收益会较高(θδ＞0)。因此，当地平均预期寿命上升时，人们会在年轻时期增加储蓄、减少个人健康投资。

(二)考虑两期效用的模型设定

接下来考虑更一般的模型设定，假设人们对年轻和老年时期的消费均有效用。此时，不仅要考虑资源在消费与健康投资之间的分配，还要考虑消费的跨期配置问题。个人的效用最大化问题变为:

其中，cyt为年轻时期的消费。此时，个人最大化问题的一阶条件为:

利用隐函数定理可得∂st/∂δ＝｜B｜/ ｜A｜，∂xt/∂δ＝｜C｜/ ｜A｜，其中｜A｜ ＞0(效用最大化问题的二阶条件)，｜B｜和｜C｜的表达式如下:

从式(12)可以看出，｜B｜的前三项均大于0，最后一项小于0。从式(13)可以看出｜C｜的前三项均小0，但是最后一项大于0。也即:

从式(12)和式(13)我们难以直接判断当地平均预期寿命对个人储蓄与健康投资支出的正负向影响。如前所述，当地平均预期寿命上升时，人们会直接增加储蓄并减少个人健康投资支出。但在两期效用的模型设定中，这两个直接效应会通过跨期消费选择进一步对家庭决策产生不同的间接效应:前者会进一步增加老年时期的消费，从而间接地增加个人预期寿命的边际收益、激励人们在年轻时期增加个人健康投资支出；后者则会进一步降低个人预期寿命水平、减少储蓄的边际收益，从而间接地激励人们在年轻时期多消费少储蓄。与只考虑一期效用的模型设定所不同的是，此时当地平均预期寿命对储蓄和个人健康投资的影响有上述直接和间接两个渠道，而这两个渠道对家户决策的影响方向是相反的。但是，如果我们考虑采用跨期替代弹性的效用函数，很容易得到与定理1 相似的结论。①因篇幅所限，本文省略了定理2 的证明，感兴趣的读者可在《经济科学》官网论文页面“附录与扩展” 栏目下载。

定理2 在考虑两期效用的模型设定中，假设u(c)＝0＜σ＜1，则有:

(2.2)若δ＋σ＞1，则有

定理(2.1)说明当地平均预期寿命(或者说公共健康水平)上升时，居民储蓄率会增加。定理(2.2)说明当δ或σ比较大时，个人健康投资会随着当地平均预期寿命(或者说公共健康水平)的上升而下降。一方面，当δ比较大时，个人健康投资支出对个人预期寿命的影响θx较小，人们通过个人健康投资来增加预期寿命的激励比较小。因此，当地预期寿命上升导致第二期消费增加后，给个人健康投资的边际收益带来的间接效应比较小。另一方面，当σ比较大时，效用函数的跨期替代弹性比较小，当地平均预期寿命上升导致年轻时期消费的下降有限。因此，为了实现老年时期消费的上升，人们会在年轻时期减少健康投资支出。另外，经过若干推导，我们可以证明dθ/dδ＞0:虽然个人健康投资会随着当地平均预期寿命的上升而下降，但是个人预期寿命还是会随着当地平均预期寿命的增加而增加。

三、数据与实证方法

(一)数据来源

本文从国家统计局城市社会经济调查总队收集的城镇住户调查(Urban Household Survey，UHS)数据获得家户的收入、消费及其他相关家庭特征数据。国家统计局每年对31 个省(自治区、直辖市)的城镇住户进行抽样调查。该调查始于1955 年，2002 年开始借鉴国际住户调查方法的先进经验，在全国采用住宅框选取调查户样本。调查单位为城镇住户，城镇是指在我国市镇建制和行政区域的基础上，按国家统计局《关于统计上划分城乡的规定》确定的城区和镇区。调查对象为户口在本地的常住非农业人口、户口在本地的常住农业人口，以及户口在外地但在本地居住半年以上的非农业人口、农业人口。城镇住户调查内容主要包括家庭人口、就业、收入、消费、储蓄、耐用消费品和住房情况等。本文的样本来自2004—2009 年16 个省区的数据，包括江苏、北京、湖北、广东、四川、甘肃、辽宁等，七大地理区域均有分布，具有较好的代表性。

本文利用中国疾控中心全国疾病监测系统死因监测数据库中的死亡率数据计算预期寿命。全国疾病监测系统始于1978 年，最初只有2 个监测点，20 世纪90 年代开始基于多阶段分层整群随机抽样原则在全国31 个省、市、自治区选择有代表性的疾病监测点组建检测系统，形成了由145 个疾病监测点组成的新DSP 系统，覆盖1000 万监测人口。到2006 年，监测点增至161 个，覆盖7000 万监测人口。全国疾病监测系统的死亡登记对象是发生在各辖区内的所有死亡个案。各级医疗机构对每一个死亡病例填写死亡医学证明书，各县区疾控中心负责对死因数据进行审核，并按照国际疾病分类规则进行根本死因确定和死因编码。①信息来自公共卫生科学数据中心网站，http://www.phsciencedata.cn/Share/ky_ sjml.jsp? id＝6b5fc 8c0-cffb-4a57-af26-a72070c65954＆show＝3。

基于死亡率数据，我们先利用简略生命表计算出各地级市人口在60 岁时的预期寿命，再将该数据与城镇住户调查数据的家户所在地级市相匹配，最终共匹配上67 座城市66 681 户样本。②详细样本情况请见《经济科学》官网“附录与扩展”。另外，本文回归分析中所控制的市级经济特征变量数据来自各年的《中国城市统计年鉴》以及各省的统计年鉴。最后，我们采用各省的CPI 指数对收入、消费、人均GDP 等进行以2000 年为基年的物价调整。

(二)实证方法

本文的回归方程如下:

其中，Yijt为被解释变量，即家户储蓄率或健康投资支出，i代表家户，j表示地区，t表示年份。Xijt是其他家户层面的控制变量，Zjt是其他城市层面的控制变量，cityj和yeart分别为城市与年份固定效应。当被解释变量为储蓄率时，我们采用最小二乘法回归；当被解释变量为健康支出时，由于有不少样本健康支出为0，我们采用极大似然法进行Tobit 模型估计。

本文的关键解释变量lifejt为地区j在第t年男性与女性60 岁预期寿命的平均值。本文研究的是老年时期预期寿命对家户年轻时期消费和储蓄决策的影响。之所以用老年时期预期寿命，一方面是因为年轻时期的死亡率都比较低，各地区差异不大。更重要的是，与理论模型相一致，本文讨论的是未来预期寿命对家户年轻时储蓄决策的影响。而出生预期寿命包含了婴儿死亡率、儿童死亡率等信息。对成年人而言，这些婴幼儿时期的死亡率并不会影响其未来的预期寿命。即使它们会影响储蓄率，渠道也与本文理论模型所讨论的未来效用贴现因子不一致。因此，本文并没有采用出生预期寿命作为解释变量。

本文回归使用的样本为户主年龄在25—60 岁(包含25 岁，不包含60 岁)且户主处于工作状态的家户。①我们选择了户主处于工作状态的家户样本。这相当于考察了目前正在工作中的年轻人的储蓄行为。我们也尝试使用25—60 岁所有家户样本，回归结果基本没有变化。解释变量为家户所在地级市60 岁时预期寿命。60 岁的年龄节点主要是从退休年龄及样本量上考虑。中国目前法定退休年龄为男性60 周岁，女性50 周岁。如果节点选太高，会使得样本中户主大多是退休人群，与研究预期寿命对年轻人消费和储蓄决策的影响不一致。如果节点选太低，会使得样本量过小。本文的分析主要以60 岁为节点展开，但在稳健性检验中，我们也分别采用55 岁及65 岁作为节点进行回归检验，结论基本一致。

此外，之所以用预期寿命而不是用死亡率作为解释变量，是因为预期寿命是基于各年龄组的死亡率，通过简略生命表计算出来的。因此，预期寿命这个指标充分考虑了死亡的年龄结构，比如在70 岁时死亡与80 岁时死亡对预期寿命的影响是不一样的。而死亡率指标将60 岁以上的死亡人口看成一个整体，并没有区分不同年龄段的死亡率。在稳健性检验中，我们尝试直接利用死亡率作为解释变量，也得到了一致的结论。

最后，回归用的预期寿命是当地当年男女性别的平均预期寿命，而没有用与户主性别相匹配的预期寿命。但在稳健性检验中，我们采用与户主性别匹配的当地男性或女性人群的平均预期寿命进行回归分析，结论基本不变。

(三)主要变量

1.预期寿命

本文通过各年龄段疾病死亡人口与总人口计算出各年龄段的死亡率，再通过简略生命表计算预期寿命。我们获得的2004—2009 年的死亡监测数据提供了以下几个年龄段的死亡率信息:0—1 岁、1—5 岁、5—85 岁每5 岁一组，以及85 岁以上。由于85 岁以上人群不再按年龄进行细分，在用简略生命表计算死亡率时，通常的做法是假设最后一个年龄组死亡事件的发生呈几何分布:85 岁以后的预期寿命就是将85 岁以上的死亡率求倒数。例如，如果某个地区85 岁以上年龄组的死亡率为0.4，就认为对于已经活到85 岁的人，接下来每年死亡的概率都是0.4，剩余的预期寿命为2.5 岁。然而，利用该办法计算出来的预期寿命明显偏高。例如，有些地区85 岁以上年龄组死亡率只有0.02，计算出来85岁时的预期寿命高达50 岁。其主要原因是把85 岁以上分为一组，分组不够细，几何分布假设不成立。另一个可能的原因是有些地区85 岁以上的总人口很少，容易存在测量误差。

为了弥补这一缺陷，我们利用60—85 岁各年龄组的死亡率来预测85 岁以上各年龄组的死亡率。具体做法为:首先采用60—85 岁各年龄组死亡率对性别、年龄等因变量进行回归，得到回归系数之后对85 岁以上各年龄组的死亡率进行样本外预测。第一步的回归方程如下:

其中，DRijt表示城市j在t年第i个年龄组的死亡率。age是所在组的年龄，例如60—65 岁组，age定义为60。式(17)相当于用年龄的三次多项式去拟合死亡率。male是性别虚拟变量。cityj和yeart分别为城市虚拟变量与年份虚拟变量。由于60 岁前各年龄组的死亡率很小，式(17)的回归只用了60—85 岁各年龄组的死亡率。

在得到式(17)的回归系数之后，我们再利用式(18)估计出各地各年份分性别的85—90 岁、90—95 岁、95—100 岁以及100 岁以上的死亡率:

基于85 岁前的原始死亡率数据以及上述85 岁以后的预测死亡率数据，我们便可以利用简略生命表计算预期寿命。①参考:孙振球、徐勇勇，《医学统计学》，2002 年第3 版，人民卫生出版社，第318—323 页。

从2004 年各年龄组分性别的平均死亡率可以看到，60 岁以前死亡率很小，60 岁以后死亡率随年龄显著上升。男性死亡率高于女性，且对于60 岁以后年龄组差异明显。从2004 年各年龄段的预期寿命可以看到，男性预期寿命明显低于女性:女性出生预期寿命平均为79.64 岁，男性为74.53 岁，女性比男性高约5 岁。②相关图例请见《经济科学》官网“附录与扩展”。从数据中也可以看出，2004—2009 年，预期寿命基本保持逐年上升趋势。男性出生预期寿命增加了1.21 岁，60岁预期寿命增加了0.79 岁；女性出生预期寿命增加了1.59 岁，60 岁预期寿命增加了0.94 岁。这说明老年时期预期寿命的延长是预期寿命增加的一个重要因素。

需要指出的是，在死因监测过程中难以避免会存在漏报现象，本文计算的预期寿命与基于人口普查数据计算出来的预期寿命相比略微偏高。但是由于我们的时间跨度不大，同一地区不同年份之间的死亡登记率差别应该不大，因此，地区性的监测误差可由回归方程中的城市固定效应来控制。另外，根据《中国统计年鉴》公布的数据，虽然利用中国2010 年人口普查数据计算出来的预期寿命男性平均为72.63 岁，女性平均为77.48岁，比本文计算出来的预期寿命略低，但是其男女性预期寿命差异约为5 岁，与本文所计算的男女预期寿命差异相一致，这也进一步说明了本文计算使用的预期寿命指标较为合理。

2.储蓄率

本文采用(可支配收入-消费性支出)/可支配收入的方法计算储蓄率，并将用此方法计算出来的储蓄率记为储蓄率Ⅰ。其中，家户的可支配收入是在总收入基础上扣除所得税和社会保障支出以及记账补贴后的收入，是家户可以用于最终消费支出和其他非义务性支出以及储蓄的总和。家户的消费性支出是指用于家庭日常生活的全部支出，包括食品、衣着、居住、家庭设备用品及服务、医疗保健、交通和通信、教育文化娱乐服务以及其他商品和服务八大类，其中购房和建房支出具有偶然性的特征，并不包括在居住支出中。由于测量误差，储蓄率会出现异常值。对此，本文参考Wei 和Zhang (2011)的做法，删除了储蓄率Ⅰ最低5%及最高5%的样本。删除异常值以后，储蓄率Ⅰ最低值与最高值都比较合理，平均储蓄率Ⅰ为24.38%，与根据宏观数据计算出来的储蓄率非常接近，说明样本具有较好的代表性。③根据《中国统计年鉴》数据，2004—2009 年中国城镇居民储蓄率从23.77%增加至28.59%。我们样本家户的平均储蓄率Ⅰ从21.96%增加到26.40%，与宏观储蓄率的变化趋势非常一致。储蓄率Ⅰ的详细分布情况，进一步说明了储蓄率的分布较为合理。①储蓄率Ⅰ分布情况请见《经济科学》官网“附录与扩展”。

在实证文献中，储蓄率有不同的算法。例如，尹志超和张诚(2019)参考现有文献，采用三种储蓄率的计算方法，第一种方法与本文的储蓄率Ⅰ相类似；第二种方法在计算消费时扣除了教育支出和医疗支出等具有很强偶然性的支出；第三种方法将储蓄率定义为家庭收入的对数减去家庭消费的对数。为了增加实证结果的可靠性，本文也计算了另外三种储蓄率作为稳健性检验，分别记为储蓄率Ⅱ、储蓄率Ⅲ和储蓄率Ⅳ。在计算储蓄率Ⅱ时，我们将家庭的消费性支出扣除教育支出和医疗支出，作为家庭的常规性消费。在计算储蓄率Ⅲ时，我们在储蓄率Ⅱ的基础上，进一步扣除家庭的耐用品消费支出，具体为家庭设备用品及服务这一大类下的耐用消费品以及交通和通信这一大类下的交通工具的购买支出。在计算储蓄率Ⅳ时，我们定义储蓄率为家庭收入的对数减去消费的对数。在这三种储蓄率定义下，储蓄率的均值都比储蓄率Ⅰ略高，这是不同计算方法导致的。②主要变量描述性统计请见《经济科学》官网“附录与扩展”。

3.健康投资支出

城镇住户调查中医疗保健支出共分了六大类:医疗器具、保健器具、药品费、滋补保健品、医疗费及其他。我们把保健器具及滋补保健品归为保健支出，并将其作为健康投资支出的代理变量，其余四类纳入医疗支出。保健与医疗支出的区别在于，保健支出是主动的健康投资，而医疗支出是健康受损后被动的投资。因此，保健支出比较符合理论模型中为延长个人预期寿命而主动进行的健康投资。家户平均保健支出约为238 元，然而保健支出有明显左截断的特征，不少家户保健支出为0。为解决由此带来的样本选择性偏误，本文将保健支出作为被解释变量的回归均采用了Tobit 模型，并用极大似然法进行估计。从为正值的保健支出样本分布情况可以看到，对保健支出取对数之后，其分布较为合理。③保健支出分布请见《经济科学》官网“附录与扩展”。

4.其他控制变量

本文家户层面的控制变量包括:可支配收入、是否拥有住房产权、人均居住面积以及人口结构信息。根据凯恩斯绝对收入理论，由于边际消费倾向递减，随着可支配收入的增加，储蓄率会增加。住房信息对储蓄率的影响不确定。拥有房屋产权的家户有可能居住支出减少，储蓄增加，但是也有可能由于财富效应而增加消费，减少储蓄。人均居住面积越大，为买房而储蓄的动机越弱，储蓄会下降。

控制的家户人口结构信息包括家户规模、抚养比④本文将抚养比定义为:抚养比＝没收入的家户成员个数/有收入的家户成员个数。、在校男孩数、在校女孩数等。家户规模可能通过影响人均可支配收入来影响储蓄率，家户规模越大，人均可支配收入越低，储蓄率越低。根据生命周期理论，抚养比越高，储蓄率越低。在校子女个数越多，子女教育及其他抚养支出越高，从而储蓄率降低。

户主自身的特征也有可能会影响其消费与储蓄决策，本文控制的户主层面的变量包括:性别、年龄、受教育程度、婚姻状况以及是否有养老和医疗保险。本文将户主的受教育程度分为四类:小学及以下、初中、高中、大学及以上，并在回归中加入了户主受教育程度为初中、高中、大学的虚拟变量。

另外，本文还控制了家户所在地级市的人均GDP 的对数，以控制地区经济发展水平对家户消费储蓄行为的影响。城市的医疗资源可能同时影响预期寿命以及家户的健康投资，因此本文还控制了地级市的每万人床位数的对数。最后，每个回归都加入了城市固定效应与年份固定效应，以控制地区与时间层面的不可观测因素。

四、实证结果

(一)基准回归结果

1.预期寿命与储蓄率

预期寿命对储蓄率的回归结果如表1 第(1)—(4)列所示。各列以不同口径的储蓄率作为被解释变量。第(1)列的被解释变量为储蓄率Ⅰ，其预期寿命的回归系数在统计学意义上显著为正，大小为0.216。①本文回归讨论的是60 岁时预期寿命对工作中年轻人储蓄行为的影响，因此回归结果并不能完全解释成宏观预期寿命每增加1 岁会导致城镇居民储蓄率增加0.216 个百分点。但由于工作中的年轻人是储蓄的主力军，且出生时预期寿命与60 岁时预期寿命在变动趋势上有很强的一致性，因此可以利用回归结果来初步讨论预期寿命增加对我国储蓄率增加的贡献。根据《中国统计年鉴》，我国居民平均预期寿命从1990 年的68.55 岁增长到2015 年的76.34 岁，共增长7.79 岁。我国同期城镇居民的储蓄率从1990 年的15.3%增加到2015 年的31.4%，上升了16.1 个百分点。根据表1 第(1)列的回归结果，如若预期寿命每增加1 岁会导致居民储蓄率增加0.216 个百分点，那么1990—2015 年预期寿命的增加会导致储蓄率上升1.68 个百分点，对同期城镇居民储蓄率增长的贡献率为10.45%。本文回归结果虽然同样表明预期寿命增长可以帮助解释我国的高储蓄率之谜，但解释力度比刘生龙等(2012)、章元和王驹飞(2019)等以往文献要小。这主要是使用的数据和方法不同所导致的。比如，本文使用了更为详细的微观家户层面数据，有可能可以更好地剔除其他与预期寿命相关的宏观变量对家户储蓄率的影响。

表1 预期寿命对储蓄率及健康投资的影响

第(2)—(4)列分别利用另外三种定义的储蓄率作为被解释变量，以进一步验证回归结果的可靠性。回归结果表明，无论在哪种定义的储蓄率下，60 岁预期寿命的回归系数均在统计学意义上显著为正，即预期寿命增加会导致储蓄率增加。以第(2)列回归结果为例，回归系数表明60 岁预期寿命每增加1 岁，会导致城镇居民储蓄率增加0.234 个百分点。

在其他控制变量上，家户可支配收入的系数显著为正，这与边际消费倾向递减相一致:随着收入的增加，用于消费部分所占的比重越来越小，而用于储蓄部分所占的比重越来越高。②在我们的理论模型中，数值模拟结果可以表明在一定参数条件下，储蓄率随着收入递增，比如当γ＝ω＝δ＝0.7，δ＝0.3，R＝1.1 时，无论是在一期模型还是两期模型中，储蓄率都会随收入而递增。这也从侧面反映了模型的合理性。人口结构上，家户规模、抚养比、在校男孩数、在校女孩数的回归系数都显著为负，与本文的预测相一致。住房产权的回归系数显著为正，说明有住房产权的家户储蓄率会更高。这与陈斌开和杨汝岱(2013)的结论是一致的。陈斌开和杨汝岱(2013)发现，由于租赁房家庭的财富水平偏低，因此储蓄率比拥有住房产权的家庭低。此外，人均居住面积的回归系数显著为负，说明人均居住面积越大，储蓄率越低，这可能是因为人均居住面积越大，为买房而储蓄的动机越弱。

在户主层面，户主是男性的家庭储蓄率比女性家庭要高，并且性别的影响对于除储蓄率Ⅱ之外的储蓄率指标都在统计学意义上显著。这与赵西亮等(2013)、Wei 和Zhang(2011)的回归结果一致。储蓄率与户主年龄的关系是呈正U 形的，在42 岁左右储蓄率达到低谷。表面上看，这与生命周期模型的结论不一致。生命周期模型预测储蓄率与年龄的关系是倒U 形的:年轻时期和老年时期储蓄率较低，中年时期储蓄率高。但需要注意的是，生命周期储蓄率与年龄的倒U 形曲线主要是由收入与年龄的倒U 形曲线所决定，而我们的回归控制了可支配收入，因此由收入变化带来的储蓄率与年龄的倒U 形曲线关系有很大一部分被可支配收入的控制项吸收了。此外，本文回归样本的户主年龄是在25—60 岁的劳动人口。储蓄率在25—60 岁与年龄呈正U 形关系，并不否认在整个生命周期中储蓄率与年龄呈现倒U 形关系。这是因为人们在25—60 岁工作时期的储蓄率会比25 岁以下和60 岁以上人群的储蓄率要高。再者，对于25—60 岁的劳动人口而言，处于中间段40 岁左右的人群，“上有老、下有小”，面临孩子上学成长、赡养老人等各种费用支出，会比25—60 岁区间中低年龄段(尚未生育子女)和高年龄段(子女已成年)人群的支出压力更大，储蓄率自然就低些。最后，本文的结论与陈斌开和杨汝岱(2013)、Chamon和Prasad (2010)，以及Chamon 等(2013)一致。例如，陈斌开和杨汝岱(2013)发现我国城镇居民储蓄率的最低点出现在43 岁左右，与本文42 岁的最低点非常接近。

受教育程度方面，在收入等其他变量相同的情况下，户主接受了初中、高中或大学教育的家庭，比户主教育程度为小学(及以下)家庭的储蓄率分别低0.9、2.5、2.8 个百分点。可能是因为受教育程度越高的家庭，未来收入的不确定性越小，因此预防性储蓄激励越低。这也与文献结论相一致。例如，陈斌开和杨汝岱 (2013)、赵西亮等(2013)都发现，我国城镇居民储蓄率随着户主受教育年限的增加而降低。另外，户主已婚的家庭储蓄率更高，但统计学意义仅对储蓄率Ⅰ显著。可能的原因是，已婚家庭对未来更加重视，所以储蓄率比未婚家庭稍高。户主有养老保险的家庭的储蓄率更低，这可能反映了两个渠道:一方面养老保险可以增加退休后的收入，从而家庭会减少当期储蓄(Feldstein，1974)；另一方面，养老保险也可以降低未来收入的风险，从而家庭会减少预防性储蓄(Hubbard 和Judd，1987)。医疗保险的回归系数显著为负，因为医疗保险可以增强家庭面对医疗风险的能力，从而降低家庭的预防性储蓄。这与甘犁等(2010)发现医疗保险能够促进家庭消费的结论一致。

在城市层面，人均GDP 和每万人床位数的回归系数均不显著。这可能是由于城市层面的经济发达程度以及医疗资源对家庭储蓄率的影响在很大程度上被城市及年份固定效应吸收了。

2.预期寿命与健康投资

预期寿命对健康投资支出的回归结果如表1 第(5)列所示。回归结果表明，预期寿命增加确实会导致家庭保健支出下降:60 岁预期寿命每增加1 岁，保健支出约下降6.4%。①需要指出的是，根据国家统计局数据，随着预期寿命的提高，家庭的医疗保健支出在不断增加。但这更多反映的是预期寿命与医疗保健支出的相关性，而非因果关系。例如，经济发展会同时带来预期寿命及医疗保健支出的增加。事实上，如果我们不加入任何其他控制变量，预期寿命对医疗保健支出的回归系数是显著为正的。而在控制了城市及年份固定效应，以及其他诸如可支配收入、人均GDP 等变量后，预期寿命的回归系数变成负值，此时得到的是预期寿命与保健支出的因果关系。可以看到，实证回归结果与模型的预测一致，地区平均预期寿命增加会使得家户相应地减少个人健康投资支出。若直接用保健支出作为被解释变量可以发现，其他条件不变时，60 岁预期寿命每增加1 岁，保健支出将在统计学意义上显著下降34 元。①保健支出未取对数的结果未展示在表格中，如有需要，可向作者索取。由于家户保健支出的水平值差异较大，取对数后能够显著改善其分布情况，因此本文的实证分析主要以保健支出的对数形式进行。

接下来，我们简单地讨论其他控制变量的回归结果。可以看到，可支配收入越高，保健支出越高。保健支出的收入弹性为2.59，比1 要大，表明保健支出是奢侈品。另外，户主是男性的家庭要比户主是女性的家庭保健支出低，说明女性更愿意将收入用于家庭的健康投资。户主受教育程度越高，保健支出越高，说明教育可能会提高人们的健康意识。保健支出与地区的人均GDP 也显著正相关，可能因为人均GDP 越高的地区人们的健康意识越强。每万人床位数对保健支出的影响也显著为正，有可能是因为城市的医疗资源越丰富，人们越愿意进行健康投资。

(二)稳健性检验

为检验回归结果的稳健性，我们对以上两个部分的回归分析做了不同的稳健性检验。①稳健性检验相关结果请见《经济科学》官网“附录与扩展”。第一，在用简略生命表计算预期寿命时，为了解决85 岁以上年龄组分组不够细的问题，本文用85 岁前的死亡率预测了85 岁以后各年龄组的死亡率。但是，预测有可能会存在误差，使得后面的回归结果有误。因此，第一个稳健性检验是在计算预期寿命时不考虑85 岁以后死亡率，只计算85 岁前的预期寿命，相当于只计算人们在60—85 岁的预期寿命。第二，在前文的回归中，我们选择的是城市人口在60 岁时的预期寿命。考虑到年龄节点的敏感性，我们选取不同的年龄节点进行回归分析。我们分别考察了55 岁和65 岁这两个年龄节点。在考察55 岁预期寿命对家户经济决策的影响时，样本为户主年龄在25—55 岁(包括25 岁，不包括55 岁)的家户；考察65 岁预期寿命对家户经济决策的影响时，样本为户主年龄在25—65 岁(包括25 岁，不包括65 岁)的家户。第三，前文回归分析中所采用的预期寿命是各地区男女预期寿命的平均值。考虑到家户中的户主可能会根据与自己同性别的群体的预期寿命来评估自己未来的寿命，并以此为根据做出家户经济决策，我们尝试把与户主性别匹配的预期寿命作为解释变量，重新进行回归分析。第四，在理论模型部分，我们假设人们在年轻时期工作并为老年时的消费而储蓄，储蓄决策受老年时期预期寿命的影响，因此在我们的回归中，不管户主年龄多大，用的都是60 岁时的预期寿命。考虑到不同年龄的户主有可能会根据自己所在年龄段的预期寿命来作决策，我们也尝试采用与户主年龄匹配的预期寿命来作回归，即把25—30 岁的户主用当地30 岁时预期寿命进行匹配，30—40 岁的户主用当地40 岁时预期寿命进行匹配，40—50 岁的户主用当地50 岁时预期寿命进行匹配，50—60 岁的户主用当地60 岁时预期寿命进行匹配，并在回归中加入代表年龄组的虚拟变量以控制生命周期的影响。第五，由于60 岁预期寿命是根据60 岁以上群体死亡率计算出来的，我们也可以直接用60 岁以上死亡率作为解释变量。②60 岁以上死亡率＝60 岁以上死亡人口/60 岁以上总人口×1 000。由于预期寿命与死亡率呈负相关关系，死亡率越高的地方预期寿命会越低。因此，死亡率的回归系数在符号上与预期寿命的回归系数应该是相反的。

以上各种稳健性检验的回归结果都与基准回归一致，表明当地平均预期寿命的增加会使得家户储蓄率显著上升，而当地死亡率的增加会显著降低家户的储蓄率，并且预期寿命回归系数的大小与表1 汇报的系数差别不大。此外，家户的健康投资支出会随当地平均预期寿命的增加而下降，随当地死亡率的增加而上升。这些稳健性检验的回归结果进一步支持了基准回归的结论。

(三)内生性问题讨论和工具变量回归

接下来我们考虑可能存在的内生性问题。内生性通常有三个来源:反向因果、测量误差和遗漏变量。本文的预期寿命是市级变量，被解释变量是家庭变量，家庭在进行消费、储蓄决策时一般将当地平均预期寿命视为外生给定的宏观经济变量，不太可能有反向因果关系。而且反向因果关系中，健康投资支出会增加预期寿命，从而使得健康投资支出与预期寿命之间存在正相关关系，与回归结果的负相关是相反的。对于测量误差问题，本文对储蓄率去了极值，对预期寿命采取了诸多度量方式，如只考虑60—85 岁间的预期寿命、用55 岁及65 岁预期寿命，以及直接用死亡率的方式，都得到了稳健的结果。而对于遗漏变量问题，回归中已经控制了家户层面及户主层面的主要信息，还控制了地区的人均GDP 及每万人床位数，同时控制了城市和时间虚拟变量以缓解地区不可观察因素及时间趋势等因素对预期寿命和家户消费储蓄行为的影响。

但为了避免仍然可能存在的内生性问题，我们进一步利用湿度作为工具变量进行回归分析。根据Barreca (2012)，极端温度有可能引起心血管或呼吸系统疾病等，而极端湿度可能会导致脱水或影响身体的散热功能。其研究结果发现，温度和湿度与死亡率的关系都是U 形的，即过高或过低的温度及湿度都会造成死亡率上升。Barreca (2012)还表明，能源消耗会对温度做出反应，但不会对湿度做出反应。因此，湿度是预期寿命的一个比较好的工具变量:首先，湿度由气象条件决定，是外生的；其次，湿度会影响本文的解释变量，即预期寿命；最后，湿度不像温度一样会影响人们的能源消耗，因此不直接影响人们的消费和储蓄行为。

本文的湿度信息来自中国气象数据网的“中国地面气候资料日值数据集”。我们首先从数据集中获得各气象站每天的气象数据；再利用地理信息系统(GIS)计算出每个县区中心位置的经纬度坐标，并基于这些经纬度坐标寻找距离最近的气象站；然后通过地级市所辖县区的气象数据求平均，得出市级层面气象信息；最后对每年的日值气象数据平均求得地级市层面各年的气象数据。回归中使用的是相对湿度指标。考虑到湿度对预期寿命的影响很可能是非线性的，我们在一阶段中加入了湿度的平方项。

工具变量回归结果见表2。表2 第(1)列报告了工具变量的一阶段回归结果，第(2)—(6)列分别报告了对不同被解释变量的二阶段回归结果。从第(1)列回归结果来看，无论是相对湿度还是相对湿度的平方项，其回归系数都在统计学意义上显著。而且相对湿度的一次项和二次项回归系数分别为正和负，说明预期寿命与湿度的关系是倒U形的:湿度较低时，湿度增加会提高预期寿命，但是湿度达到一定值后再增加会导致预期寿命下降。这个回归结果与Barreca (2012)的结论非常类似。此外，为了检验工具变量的合理性，我们还进行了弱工具变量以及过度识别检验，结果表明可以认为不存在弱工具变量以及过度识别问题。①在弱工具变量检验中，Cragg-Donald Wald F 值为415，Kleibergen-Paap rk Wald F 值为27.30，均大于10%临界值19.93。在过度识别检验中，Hansen J 统计量为1.4，其p 值为0.23，因此接受原假设，认为如果有一个工具变量是外生的，那么另一个也是外生的，不存在过度识别问题。

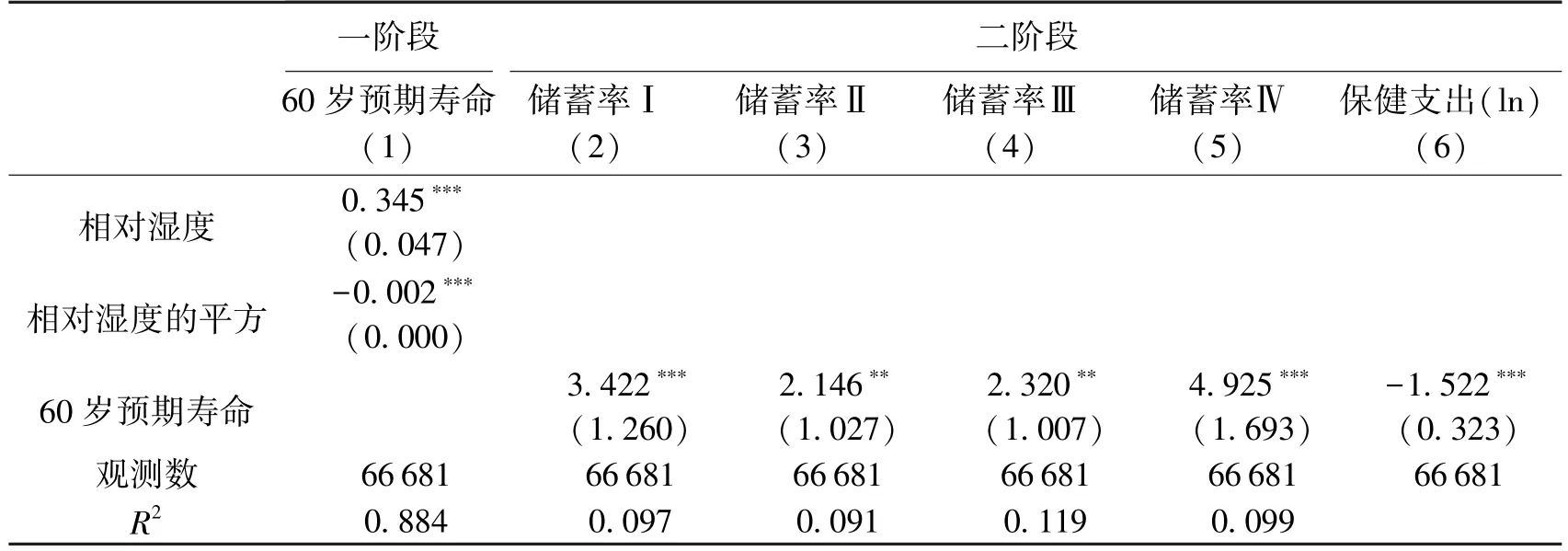
表2 工具变量回归结果

第(2)列及第(6)列的二阶段回归结果表明，预期寿命增加会导致储蓄率统计学意义上显著增加，保健支出在统计学意义上显著下降。运用工具变量克服可能的内生性问题后，回归系数的符号及显著性都不变，说明本文的结果是比较稳健的。但同时我们也看到，运用工具变量后预期寿命回归系数的绝对值比之前的都大。可能的原因是，运用工具变量识别出来的是预期寿命受湿度影响的群体的效果，即局部平均效果。如果预期寿命受湿度影响大的地方，预期寿命对居民储蓄率的影响相对也大，那么就有可能出现工具变量回归值偏高的情形。此外，尽管文献表明湿度并不直接影响居民能源消耗，但现实中居民有可能通过使用抽湿机、加湿器等设备来降低极端湿度的危害，因此并不能完全排除湿度会直接对储蓄率带来影响的可能性。综合以上原因，本文的工具变量回归仅作为基准回归的补充，可以进一步验证本文结论的可靠性。

五、结论

自改革开放以来中国经济保持高速发展，而探讨其背后原因和机制具有重要的意义。大量文献研究表明，一国的预期寿命水平对于其长期经济增长有显著的正向影响。通过对家户行为的理论建模和基于家户微观调查数据的计量检验，本文从微观家户角度来理解公共健康与经济增长关系的微观基础，并提供相关实证证据。

本文运用两期世代交替模型，从理论上探讨预期寿命对家户储蓄和健康投资行为的影响，推断出预期寿命上升可以使得未来效用的贴现因子增加，从而导致储蓄上升；预期寿命越高，个人预期寿命提升的空间越小，个人健康投资支出会下降。为验证该理论模型，我们进一步利用2004—2009 年全国城镇住户调查提供的家户信息和全国疾病监测系统死因监测数据库提供的死亡率信息对理论模型的推导结果进行实证检验。回归结果发现，预期寿命确实会带来家户储蓄率的上升和健康投资支出的下降。平均而言，60 岁预期寿命每增加1 岁，传统口径下的储蓄率增加0.216 个百分点，保健支出下降6.4%。多项稳健性检验都证明了这一结论。为了解决可能存在的内生性问题，本文还利用相对湿度作为工具变量，得出的结论一致。

根据本文的研究结果，预期寿命上升会增加居民的储蓄率。由于家户储蓄是投资的主要资金来源，居民储蓄率增加会拉升投资。因此，中国经济的高速增长，很可能可以部分归因于公共健康水平提高带来的预期寿命上升。另外，我们的研究结果表明，预期寿命代表的公平健康水平会降低个人健康投资，说明公平健康水平与个人的健康投资在一定程度上存在替代关系。由于个人健康投资的收入弹性大于1，属于奢侈品，公共健康水平的增加有可能会缩小低收入水平居民与高收入水平居民的健康差异，从而促进社会的平等化发展。因此，无论是从经济增长还是从社会公平角度来看，将健康作为国家的发展战略都有重要的社会意义。当然，预期寿命增加对于经济增长以及居民健康水平差异的影响仅是基于本文回归结果所作的推测，要得到严谨结论还需可靠的实证分析，这可以作为未来进一步的研究方向。