射流泵喉管结构优化及模型放缩机理研究

2023-12-28孙琬婷

流体机械 2023年11期

孙琬婷，李民

（昆明理工大学机电工程学院，昆明 650500）

0 引言

射流泵具有结构简单，加工成本低，密封性好等优点，被广泛应用于农业、水利、冶金、石油勘探等领域［1］。由于不存在运动部件，射流泵的效率往往不高，其较低的效率成为制约射流泵应用的主要缺点，因此诸多学者通过优化射流泵的结构参数设计以提升其总效率［2］。对射流泵结构优化的研究常常采用数值试验和模型试验方法，以往的文献表明，CFD 技术已广泛应用于水射流、射流泵、射流空化等领域的研究，并具有良好的精度［3-7］。但由于数值试验的理论方法尚存在一定的局限性，数值计算结果最终仍要由试验来验证，因为原型试验存在测量困难、经费开支大的问题，试验研究往往采用放缩性的模型试验［8-9］。国内学者陆宏圻在其专著中对射流泵基本方程、相似律等进行系统性论述，流体机械的放缩过程应遵循几何相似、运动相似和动力相似［10］。

国内外学者对射流泵的喷嘴、喉管入口、喉管距、面积比、扩散管和吸入室做了大量的理论和试验研究［11-14］，但对射流泵的喉管倾角的研究较少。本文通过数值计算与模型试验相结合的方法探究射流泵喉管倾角和长度比的耦合关系及其对泵送性能的影响，并探究射流泵模型试验放缩过程的相似性机理，确定放缩模型试验的等效动力参数，以确保放缩模型试验的有效性。根据数值计算结果，分析不同喉管倾角对泵送效率的影响以及射流泵内部压力变化，并进一步探究不同喉管倾角在不同长度比下的耦合关系，试图得到喉管倾角、长度比与流量比耦合的最优设计参数及适用范围。

1 参数

1.1 结构参数

如图1 所示，典型的流体射流泵可由工作喷嘴、吸入室、喉管和扩散管4 个部分组成，喉管长度为175 mm、喉管直径为25 mm。倾角为0°和4°的射流泵被作为基准射流泵，用以表征喉管倾角参数改变带来的性能提升。

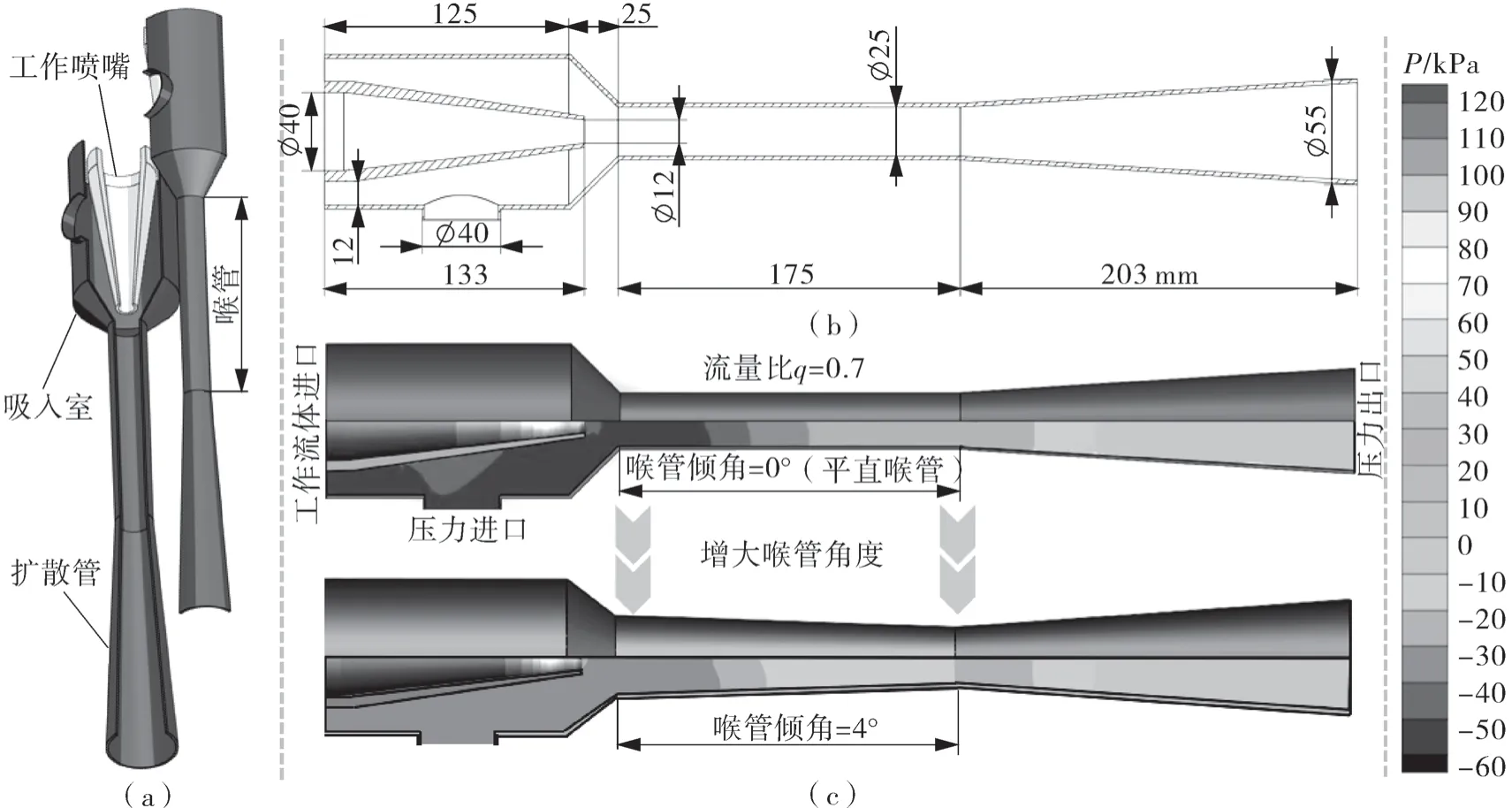
图1 射流泵的几何结构及泵内压力分布云图Fig.1 Influence of the geometry and structural changes of the jet pump on the pressure in the pump

1.2 射流泵无因次参数

射流泵的流量、压力及主要几何参数，用下列无因次值表示。

流量比：

压力比：

面积比：

效率：

式中，Qs为射流泵的吸入流量；Q0为工作流量；Pc为射流泵出口管路压力；Ps为被吸液体管路入口压力；P0为工作液体管路入口压力；A3为喉管截面面积；A1为喷嘴出口面积。

2 数值计算方法

2.1 数值模型的建立

本研究采用压力基稳态求解器模拟流场，基于质量方程、能量方程和输运方程的k-epsilon 湍流模型也被采用，定常的湍流控制方程为：

式中，∅为未知函数u，v，k，ε。

朱劲木［15］将此控制方程的系数及模型常数进行了总结。为了方便计算，采用喷嘴出口半径r0为特征长度，喷嘴出口断面平均流速u0为特征速度，将控制方程无量纲化。再将物理平面上的控制方程转换到计算平面上，得到下列混合有限分析法形式的控制方程。

连续性方程：

其中，U =urη-vxη，V =vxξ-urξ，J =xξrη-xηrξ。

动量方程：

式中，各方程系数可见文献［16］。

射流泵的动量项采用二阶迎风格式进行离散，湍动能及湍动能耗散率均采用一阶迎风格式进行离散，压力速度耦合采用SIMPLE 算法，所有变量收敛残差均为1×10-6。将整个射流泵的边界划分为进口边界、出口边界和固壁边界。进口边界：将所有液体进口设为速度入口，设置距喷嘴出口上游120 mm 处为无穷远均匀来流，以保证来流稳定，来流速度方向与进口边垂直；出口边界：设置为压力出口，为保证流场出口的稳定，在扩散管后增加了200 mm 的直管段；固壁边界：采用壁面函数法。

2.2 网格划分及无关性分析

根据射流泵内部流动特性分布进行网格划分。射流泵吸入室部分存在较大的湍动趋势，所以选用对紊乱流动更为敏感的非结构化网格划分区域；其他流体结构流动过程较为平缓，所以选用结构化网格，具体的网格划分如图2（a）所示。

图2 射流泵计算域网格划分及合速度分布Fig.2 Domain meshing and closing velocity distribution for the jet pump

为进行网格无关性研究，本研究对基准射流泵的计算域完成了6 种不同密度的网格划分，并选择其中心旋转线作为监测线进行监测，如图2（a）（b）所示。随着网格密度的增加，监测线上的速度逐渐稳定，如图2（c）所示，本研究选用220 万网格完成对后续所有几何结构射流泵的网格划分。

2.3 可视化模型试验

本研究通过可视化模型试验、泵送效率试验进行数值模型的准确性验证。结果表明，数值模型在泵送效率上的误差最大仅为2.8%，完全满足了计算需求。

可视化模型试验使用的试验器材包括水泵、稳压器、流量计、压力表、射流泵、纯橡胶小球、配套管路。使用的射流泵为标准射流泵的几何相似模型，尺寸为原尺寸的1/2，泵体水平放置。本试验是将纯橡胶小球由射流泵入口泵入，通过摄像机记录小球的运行轨迹并与计算结果的流线相对比以实现验证。纯橡胶小球的密度为0.93×103kg/m3，接近与水的密度，可以最大程度上减少小球对流场带来的影响，并接近泵送流线。试验使用的动力参数如下：工作流体流量为6.5 L/min，表压为130 kPa；泵入流体的流量为4.5 L/min，表压为-6.4 kPa；两者的压力比为0.235；射流泵泵入口距水平面的高度约为65 cm。其中，射流泵泵入口的压力由式（8）估算。射流泵动力参数均满足运动相似和动力相似的特性，具体论证可见第3.1 节。

式中，Z 为距水面高度；u 为平均流速；下标1 为储水罐上截面；We为输入的功；下标2 为射流泵泵入截面；hf为阻力做功。

本研究开展泵送效率试验，通过记录上述试验过程泵送入口和卷吸入口的压力，计算出射流泵的压力比，与计算结果相对比以验证放缩前后射流泵的运动相似性，进一步论证数值模拟的准确性。

3 结果与讨论

3.1 放缩过程的相似性定理

本节主要探究射流泵放缩过程中，如何根据几何相似、运动相似和动力相似确定泵送特性参数，以及如何进行流态相似性的验证。其中几何相似用以确定设备尺寸，运动相似用以验证试验参数的准确性，动力相似用以确定设备动力参数。最后将满足相似性定理的放缩模型试验结果与数值模拟结果相对比，完成数值模拟准确性的验证。

3.1.1 几何相似性和运动相似性

可视化模型试验中射流泵的线性尺寸为数值模拟模型线性尺寸的1/2，相应角度相等，为标准的几何相似模型。本节对放缩前后的射流泵的运动相似性进行了讨论，以完成对上文试验参数的准确性验证。首先，判断其运动轨迹是否相似；然后，验证泵送量与压力比的耦合关系。

用密度与水相似的纯橡胶小球对射流泵吸入流体的运动轨迹进行跟踪与确定，并将其随时间的变化通过堆叠的方式进行展示，其运动轨迹可以与计算结果的多条流线相对应，如图3 所示。由流动轨迹可以看出流体被吸入后以较慢的速度绕喷嘴环状旋转，最后至喷嘴出口断面处与工作液体合流泵送出射流泵，该运动过程与计算结果相似，这证明其流动状态相似。

图3 可视化试验与数值计算的对比结果Fig.3 Comparison results of the visualization experiment and numerical calculation

FRIDMAN［17］根据实验资料拟合出了射流泵基本方程，如下式所示：

式中，q 为流量比；a，b 为试验系数，其中a=km+c，k=0.516，面积比m=喉管截面面积/喷嘴出口面积，b=（2.348m+1.547）/（m2+2m），c=0.34；β 为射流泵水头与喷嘴出口断面水头之比。

射流泵工作流体入口压力已知，泵入流体入口压力可由式（8）计算得出，射流泵的压力比为0.235。将试验压力比0.235 代入式（9）可得射流泵理论流量比为0.67，接近试验比值的0.69，精度为97.2%，证明了放缩前后射流泵的运动相似性。

3.1.2 动力相似性

动力相似是表征不同流动体系具有相同的流动状态的重要标准。两个不同流动体系的无量纲评价结果具有相似性，这说明上述两力学系统满足微分方程且具有相似的边界条件和定解条件。以往常用雷诺数来衡量动力相似，但水射流泵实际的泵送过程是有压流体做功帮助被吸流体克服重力势能的过程，由于弗劳德数为惯性力与外力的比，该参数比雷诺数更侧重于外力对流体产生的影响，因此选用工作流体入口处的弗劳德数以确定系统的动力学参数。在射流泵工作流体入口处，工作流体受到外力可以近似看成其受到的压力，此时弗劳德数的具体计算公式如式（10）所示。若射流泵的放缩前后，其弗劳德数相似，则该计算公式可简化为式（11）。在数值计算尺度下，工作流体的泵入流速为1.77 m/s，泵入压力为130 kPa，将该数代入式（11）中，可以得到试验尺度下，满足弗劳德数相似的射流泵工作流体泵入流速和压力间的耦合关系，如式（12）所示。

Fr1=Fr2，则有：

式中，Fr 为弗劳德数；u 为工作流体的平均流速；ρ为工作流体的密度；P 为射流泵入口处工作流体的压力；d 为喉管直径；L 为入口直径；ε为试验与计算模型的放缩比；下标1 为试验尺度；下标2 为数值计算尺度。

本研究使用的试验设备可以在泵入压力为20.8 kPa 的条件下提供流速为0.5 m/s 的工作流体；该工作参数满足弗劳德数相似的技术要求，并同时满足运动相似的要求。

3.1.3 放缩过程流态变化的讨论

本研究使用雷诺数、Craya-Curtet 数Ct、以及涡量等势面Q 准则对放缩前后流态相似性进行了讨论。雷诺数是典型的衡量流场中惯性力和黏性力比值的无量纲物理量，雷诺数的计算如式（13）所示。在数值模拟下，射流泵最大流速出现的喷嘴出口处，最大流速接近19.5 m/s，最大雷诺数为780；在试验下，最大流速接近5 m/s，最大雷诺数为100。说明放缩前后的流态大致相同，且均处于层流状态。

式中，ρ为流体密度；v 为流场的特征速度；L 为流场的特征长度；μ为动力黏性系数；Rec为转捩雷诺数。

HILL［18］使用Craya-Curtet 数Ct 来判断射流泵的流态，如下式所示：

由该式可知，流体在面积核定的圆管内以稳定状态进行流动时，Ct 数显然为定值；若管道截面积恒定，管道内速度波动规律稳定，则可以将Ct（u，A）的函数转换为Ct（u）的函数。对于稳定的泵送过程而言，管内流体的速度是处于不断发展的过程，如果将泵内任意截面的平均速度视作入口流速的R 倍，则对于任意截面Ai而言，其速度关系式如式（15）所示，此时可以将Ct（u，A）的函数转换为Ct（R）的函数：

为便于表征射流泵内的相对位置，本研究引入比例距离，该值是指射流泵中心轴上的一点距中心轴左端点的距离与射流泵总长度的比，如下式所示：

图4 示出了放缩前后泵内速度变化及流场涡量。

图4 放缩前后泵内速度变化及流场涡量Fig. 4 Velocity change and flow field vorticity in the pump before and after scaling

从图4 可见，放缩前、后射流泵内流体速度波动具有相似性，且泵内的速度波动主要集中于喉管段内。研究射流泵内流体的速度波动可以通过研究喉管段流体的速度波动近似代替，而速度的波动则可以用比例系数的波动相代替。由于速度波动的方向相对较为复杂，且速度波动方向可以划分为径向波动和轴向穿透，本研究将系数R 划分为径向系数和轴向距离。如图4（a）所示，比例距离相同，放缩前后射流泵内流体的轴向速度波动范围及其速度值相似；在喉管部分确定一个监测线以检测径向合速度的变化趋势，如图4（b）所示，放缩前后的射流泵流体的径向合速度波动趋势相似，这证明轴向速度的波动不会对系数R造成较大的影响。

满足以上两点要求，则系数R 不变，进而Ct 数也不会发生改变，从而证明放缩前后的内部流动状态较为稳定。图4（c）示出放缩前后，射流泵内部流场的Q 准则下的涡量。可以看出放缩前后，泵内流体的涡量分布趋势并无明显变化，涡量主要集中在吸入室内呈散状分布，其余少量分布于喉管段内。总的来说，无论是从流态分布还是涡量分布的角度，放缩前后射流泵均具有较好的相似性。

综上所述，在进行射流泵放缩过程时，满足几何相似即可保证特征方程不变，满足弗劳德数相似即可保证流态不变，运动相似的满足与否可以用于上文的验证过程。

3.2 喉管倾角的影响

在传统射流泵设计过程中，为了便于生产加工一般不设计喉管角度，统一设计为平直的0°。随着机械加工技术的提高以及节能减排的现实任务要求，增加射流泵倾角带来性能上的提升不可忽略。

本研究选用喉管直径为25 mm，喉管长度为125 mm，喉管倾角分别为0°、2°和4°的射流泵来探究倾角改变对泵送效率的影响，以及探究喉管角度与流量比之间的耦合关系。

3 种几何尺寸的射流泵，其泵送效率随流量比之间的耦合关系如图5 所示。喉管的最佳倾角与射流泵泵送流量呈正相关，即具有更大倾角的射流泵泵送效率随流量比变化而产生的拐点会更晚出现；但当喉管倾角过大时，其最高泵送效率呈现凸函数的趋势，即先增大后减小。具体来说：在流量比小于0.8 时，射流泵的泵送效率随着喉管角度的增大而递减，喉管角度为0°时整体的效率最高，泵送效率值为26.08%，如图5（a）段所示；但在流量比大于0.8 的情况下，平直喉管结构射流泵的泵送效率开始逐步递减，而2°和4°喉管倾角结构的射流泵泵送效率仍在逐步攀升；当流量比大于0.9 小于1.1 时，2°倾角的泵送效率实现反超，整体效率最高，并达到三者全域最高值26.15%；当流量比大于1.1 之后，倾角为4°的泵送效率最高，最高值为25.53%；自流量比大于0.955起，0°倾角的泵送效率为三者最低，如图5（b）段所示。由此表明：（1）喉管倾角的改变可以提高泵送效率；（2）在小流量比工况下平直喉管结构最优，但在大流量比工况下，有倾角的喉管结构能带来13%的泵送效率提升。

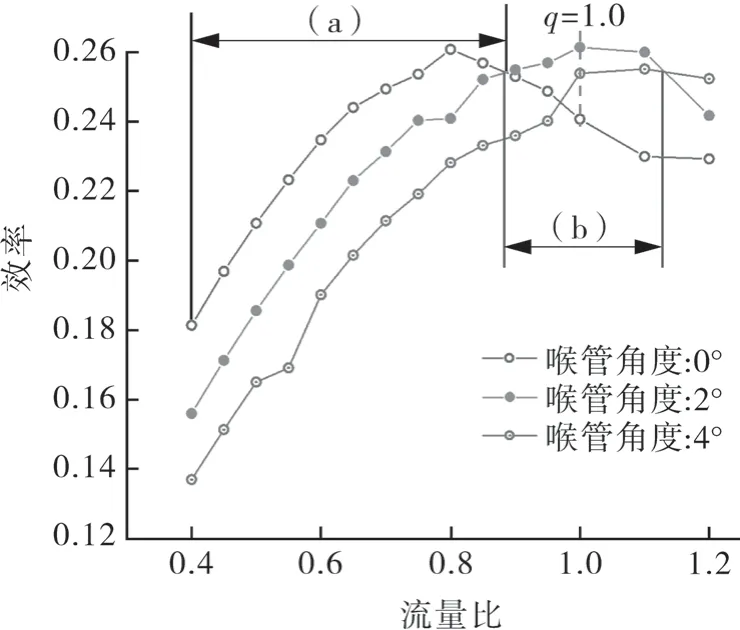
图5 射流泵喉管结构倾角对泵送效率的影响Fig.5 Effect of the inclination angle of the jet pump throat structure on the pumping efficiency

在卷吸流量较小的情况下，增加射流泵喉管处的倾角相当于增大了喉管外围的直径，这样会造成流体动量的折损，表现为喷嘴处静压的提升进而难以高效的完成泵送任务。但随着流量比的增大，得益于拉乌尔效应，射流速度将增大，喉管段压强降低，促进液体的卷吸，从而提升效率。图6 示出流量比为1.0 时，喉管角度为0°和2°的2 种射流泵的中轴截面处的压力云图。0°和2°的射流泵喉管中段与压力入口处的平均压力差分别为15 和13 kPa，此时，高倾角射流泵可以在更小的压差下泵送同等流量的液体，具有更好的泵送性能。

图6 射流泵喉管结构倾角对内部压差的影响Fig.6 Influence of inclination angle of jet pump throat structure on internal pressure difference

3.3 大流量比工况下长度比和倾角的关系

在化工生产过程中会因工艺要求而提出较大流量比的要求。例如，在造纸生产过程中，浓纸浆和水必须以一定比例混合，才能造出一定浓度的纸浆；在重油气化造气生产过程中，进气化炉的氧气和重油应保持一定的比例，否则可能会发生爆炸事故。因此在特殊流量比下，尤其是在大流量比条件下，对射流泵进行结构优化不可忽略。

在大流量比［0.9，1.2］下，有倾角结构的射流泵显然具有更优异的性能，这与传统流量比［0.4，0.9］工况下，平直喉管射流泵具有最优效率不同。国内外诸多学者已经对平直喉管结构射流泵进行了较为全面的研究，而对大流量比工况友好的有倾角射流泵的研究甚少，本研究在前文的基础上选用喉管直径d=25 mm，喉管长度分别为4d，5d，6d，7d，8d，即长径比分别为4，5，6，7，8，喉管倾角分别为0°，1°和2°的射流泵，进一步探究在大流量比工况下，喉管倾角与喉管长度比的耦合关系对泵送性能的影响，进一步探究喉管倾角优化的意义。

由喉管倾角和喉管长度比参数不同取值组合而成的15 个射流泵在大流量比［0.9，1.1］下的耦合关系，及其泵送性能如图7 所示。在0°倾角结构下，长径比为5～7 的整体效率较高且方差较小，泵送效率对长径比的依赖性较弱，长径比为7 时拥有最高效率，如图7（a）所示。在1°倾角结构下，泵送效率与喉管长径比呈负相关，长径比越大，整体泵送效率越低，长径比为4 时拥有最高效率，如图7（b）所示。在倾角为2°结构下，泵送效率与长径比关系产生波动，随着长径比的增大，整体泵送效率出现波动趋势，长径比为5 时拥有最高效率，如图7（c）所示。在各个角度的射流泵结构下，长径比为4 的射流泵效率易出现“断崖式”下降，长径比为5～8 时结构的泵送效率较为平缓。

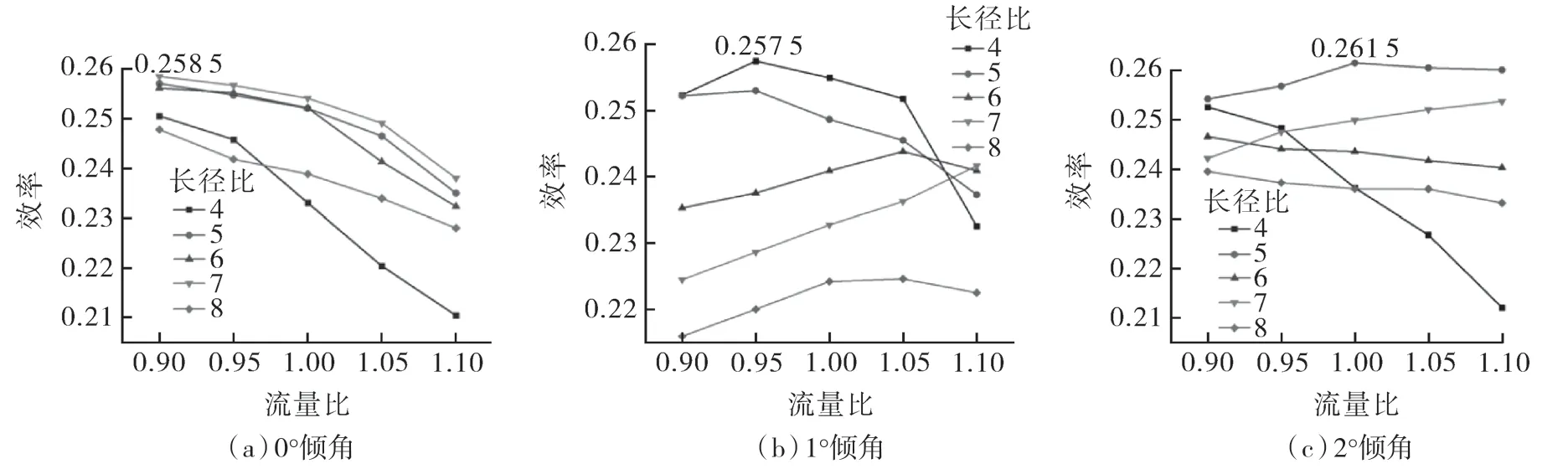
图7 大流量比工况下长径比和倾角的耦合关系Fig.7 The coupling relationship between length ratio and inclination angle under large flow ratio conditions

本研究将不同角度的最高泵送效率所对应的长径比曲线进行对比，结果表明，倾角为1°、长径比为4 的结构在流量比［0.95，1.05］的范围内泵送效率比0°倾角所对应的最优长径比7 带来的泵送效率更高；倾角为2°、长径比为5 的射流泵结构的整体泵送效率最高，此时，相对于倾角为0°的射流泵在长径比为4～8 全域的最优泵送效率，泵送效率提升了3%，喉管段长度降低了28.6%。这说明喉管倾角的改变不仅使射流泵更适用于大流量比工况，还能以更短的喉管长度获得相同甚至更大的泵送效率，一定程度上减少了喉管段的材料成本。