轴流式两级一体化水力旋流器结构参数优选
2023-12-28张晓光刘佳成徐保蕊赵立新司书言蒋明虎
张晓光,刘佳成,徐保蕊,赵立新,司书言,蒋明虎
(1.东北石油大学 机械科学与工程学院,黑龙江大庆 163318;2.黑龙江省石油石化多相介质处理及污染防治重点实验室,黑龙江大庆 163318)
0 引言
当前水力旋流器广泛应用于能源、化工、食品工程及废水处理等行业领域[1-9]。研究者对油水分离用水力旋流器开展了大量的研究[10-16]。如PEREIRA 等[17]将旋流器应用于井下油水分离,处理后水可直接注入地层。程海鹰等[18]对水力旋流器油水分离技术开展了研究,并进行了现场实际应用测试。
在采油井筒井下等有限空间开展油水分离用水力旋流器设计方面,由于轴流式结构特有的轴向进液形式,已成为该领域研究热点。在新型轴流式水力旋流器研究方面,研究者不断改进和优化结构设计,以适应特殊空间的应用和效率提升。丁旭明等[10]开发的新型轴流式旋流分离器有效地降低了入口处局部阻力损失。YOSHIDA等[19]通过试验对比了传统旋流器和螺旋进口旋流器的分离性能,发现螺旋进口旋流器分离效率较传统型式有明显提高。JI 等[20]研究发现螺旋线型进口既能抑制颗粒错位,又能降低能量损耗。NIEUWSTADT 等[21]推导了轴流式分离器简化分离效率理论公式,认为减小导向叶片之后的筒体直径可提高分离效率。蒋明虎等[22]研究发现螺旋叶片入口较切向入口具有更高分离效率和较低压损。潘威丞等[23]模拟了叶片个数对流场的影响,为旋流器结构设计提供了参考。VAUGHAN[24]也提出了一种基于螺旋叶片的入口结构,可满足小处理量、细颗粒的分离需求。徐保蕊等[25-26]设计了一种螺旋油水分离器,进液结构亦采用螺旋叶片式轴流入口,研究发现该结构具有流量波动适应范围宽、径向尺寸小以及强螺旋流分离效率高等优势。
然而,轴流式入口结合螺旋结构的水力旋流器内部结构设计复杂,涉及的结构参数较多,因此有必要开展一体化设计及关键参数优选研究。基于此,本文提出一种轴流式两级一体化水力旋流器,对其结构参数进行优选,并重点探究其内部流场特性,确定具有更高分离效率的旋流器结构,研究可为旋流器进一步优化设计与应用提供参考。
1 物理模型及分离原理
基于旋流分离原理设计出一种轴流式两级一体化水力旋流器,如图1 所示,主要包括一级螺旋流分离结构和二级螺旋内锥结构。一级螺旋流分离结构轴向距离短,以快速分离大粒径油相为主;二级螺旋内锥结构,轴向长度较长,以强化难分离小粒径油滴颗粒为主。旋流器整体流体域模型及分离原理如图1(a)所示,油水两相由轴向进入,经一级螺旋流分离结构中螺旋叶片将轴向流动转为切向速度为主的螺旋流,螺旋流场中低密度油相向中心汇集形成油核,通过二级螺旋内锥结构中心的一级溢流管流出;一级预分离的剩余油水混合物继续经过二级螺旋内锥结构进行强化分离,其中更多难分离的小粒径油滴在离心力驱动下向中心方向汇集至内锥结构并聚结,最终与一级溢流管分离出的油相在总溢流管处汇合流出。水相由底流口流出,完成油水二级分离。
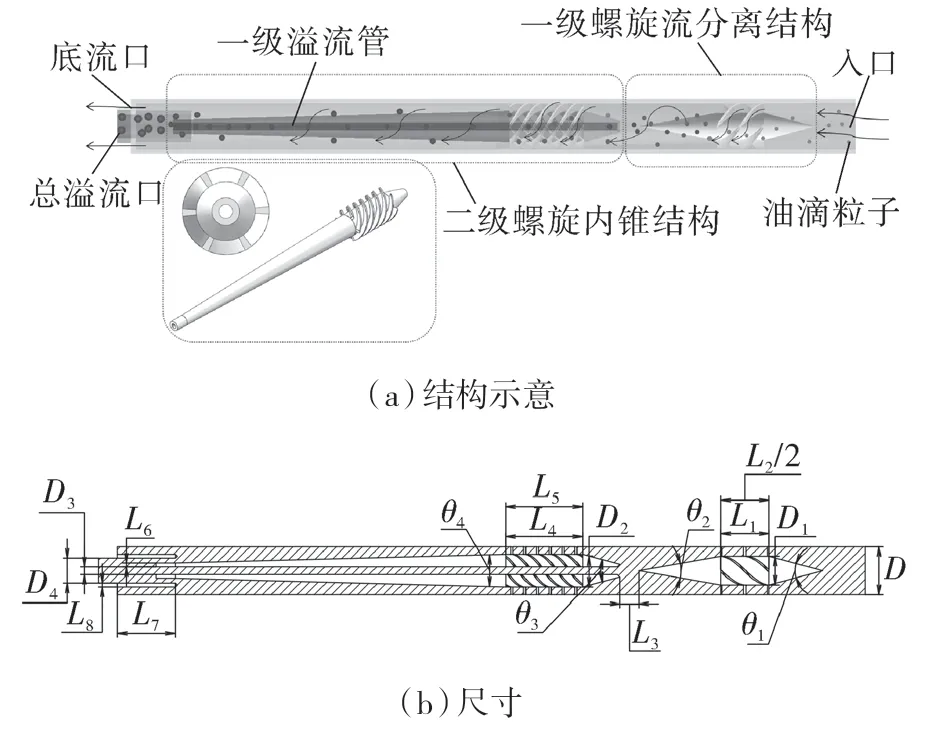
图1 轴流式两级一体化水力旋流器结构设计Fig.1 Structural design of axial-flow two-stage integrated hydrocyclone
本文研究模型主直径D 为50 mm,初始结构各结构参数如图1(b)所示,具体尺寸见表1。其中一级螺旋结构叶片数为4,二级螺旋叶片数为6。

表1 轴流式两级一体化水力旋流器主要结构参数Tab.1 The main structural parameters of the axialflow two-stage integrated hydrocyclone
2 网格划分及无关性检验
利用Solidworks 软件建立轴流式两级一体化水力旋流器流体域模型,旋流器整体采用六面体网格划分,如图2 所示,在一级稳流锥和导流锥局部采用四面体网格划分。通过调整间隔尺寸控制流体域模型网格总数。对流体域进行不同水平网格划分,各水平对应的间隔尺寸与网格数量见表2。

表2 不同水平网格划分数量Tab. 2 Number of grid division at different levels

图2 模型网格划分Fig.2 Mesh division model
针对不同网格水平的模型施以相同边界条件进行计算,待收敛后进行网格无关性检验。溢流压降ΔP1是反映旋流器分离性能重要指标之一,为此以轴流式两级一体化水力旋流器ΔP1为考核指标,分析网格数对ΔP1的影响,得出溢流压降ΔP1随着网格数变化的对比曲线如图3 所示。可见,当间隔尺寸从1.90 到1.74 时,旋流器ΔP1呈上升趋势,当间隔尺寸达到1.65 后,ΔP1趋于平缓,当间隔尺寸为1.60 时,相较于1.65 时ΔP1基本不变。为节约计算成本,最终选用1.65 间隔尺寸进行网格划分。

图3 不同网格划分水平的旋流器溢流压降Fig.3 Overflow pressure drop with different grid division levels
3 参数设置与模型验证
3.1 模拟参数设置
模拟介质为油水两相流,介质参数分别为连续相水相:密度为998 kg/m3、黏度为1 mPa·s;离散相油相:密度为859 kg/m3、黏度为1.03 mPa·s,体积分数为5%。
采用ANSYS-FLUENT 软件进行数值模拟,入口边界条件为速度入口(velocity),通过调整处理量控制入口速度。计算处理量为5 m3/h 时所对应的入口速度vi,计算式如下:
式中,Q 为入口流量,m3/h;A 为入口过流面积,m2。
溢流口和底流口均设置为自由出口(outflow)。溢流分流比是针对入口总进液量进行分流的,设置为30%。选用压力基准算法隐式求解器稳态求解,湍流计算模型为雷诺应力模型(Reynolds stress model,RSM),油水两相间模拟计算采用多相流混合模型(Mixture)。SIMPLEC 算法用于进行速度压力耦合,动量、湍动能和湍流耗散率为二阶迎风离散格式,收敛精度设为10-7,壁面为不可渗漏无滑移边界条件。
3.2 模型验证
本文所设计结构以螺旋导流产生螺旋流分离流场为主,与文献[22]设计的螺旋分离器结构核心近似,因此本文模拟湍流模型等设置也与该文献一致,根据文献中的PIV 试验所得数据与模拟所得数据对比如图4 所示(图中径向位置采用无量纲化处理,r*=2r/D),模拟与试验结果吻合良好,验证了本文模拟计算的可靠性。

图4 入口管段轴向速度沿径向位置分布对比Fig.4 Comparison of the distribution of va along the radial position of the inlet pipe section
4 结果分析
4.1 不同结构参数对质量效率的影响
分别对一级到二级距离L3、一级导流锥锥角θ2、一级溢流管内径D4、一级螺距L2、二级螺距L5、二级导流内锥锥角θ4、总溢流管内径D4、总溢流管伸入长度L7、二级稳流锥锥角θ3等结构参数进行数值模拟,系统分析轴流式两级一体化水力旋流器的质量效率随结构参数的变化规律,如图5 所示,其中质量效率Ez计算式为:

图5 各结构参数对质量效率的影响Fig.5 Effect of various structural parameters on mass efficiency
式中,Mu,Mi为溢流口、入口油相质量,kg/s。
由图中可知,优选前初始模型的质量效率为57.38%,溢流压降为31.18 kPa,经优化后,旋流器最高效率可达到96.38%,溢流压降为89.42 kPa。旋流器分离效率基本随着各参数的变化呈现先增大后减小的趋势。其中较为特殊的是,旋流器二级稳流锥锥角结构参数的变化对效率影响规律呈先减小后增大然后再减小的趋势,且二级稳流锥锥角的变化对质量效率的影响也比其他参数更大,因此本文重点对二级稳流锥锥角对旋流器流场的影响以及出口压降与质量效率的关系做进一步分析。
4.2 二级稳流锥锥角对流场的影响
在保持其他参数不变的情况下,分别改变二级稳流锥锥角θ3为12°,18°,24°和30°,对不同参数建模和模拟,对比探讨θ3对旋流内流场、压降及效率的影响规律。
由图6 可知,在不同二级稳流锥锥角参数下,油相体积分数在腔体内分布区域基本相似,但分布的量值不同。在一级螺旋流分离结构区域,油相浓度分布程度基本一致;而在二级稳流锥锥角为18°和30°时,二级稳流锥锥角上端有油相的聚集,可推断此处产生了不同程度的循环流。在二级稳流锥锥角为12°~24°时,油相在二级螺旋内锥结构和总溢流口之间部分出现了较高体积分数油相的聚集,且二级稳流锥锥角为12°和24°时更为明显。取二级螺旋流道下方5 mm 处为截面一和总溢流口上方10 mm 处为截面二,对比不同锥角参数下,截面一和截面二上的油相分布变化,可见:(1)在二级稳流锥锥角为12°和24°时,截面一处靠近二级导流内锥壁面的油相浓度明显提高;(2)截面二处在旋流器径向直径为15~20 mm之间出现一油相浓度较高的环形条带,当二级稳流锥锥角为12°,24°和30°时,截面二靠近二级导流内锥壁面处油相浓度明显升高,而二级稳流锥角为12°和24°时,油相浓度集中的范围更大。

图6 不同二级稳流锥锥角参数下油相体积分数分布云图Fig.6 Cloud diagram of oil phase volume fraction distribution under different second-stage steady flow cone angle
选取截面一和截面二的切向速度进行对比,由图7 可知,两处切向速度沿径向分布趋势基本一致。在一级溢流管中旋流器的切向速度基本没有变化,在二级导流内锥边壁附近切向速度近似呈现自由涡-强制涡的组合涡特征,内外旋流分布明显;切向速度在二级导流内锥边壁附近处数值最小。其中二级稳流锥角为12°和24°的旋流器两截面切向速度基本相同,外旋区域的切向速度相对于二级稳流锥角为18°和30°旋流器内的更高。而二级稳流锥角为12°和24°旋流器的内旋区域切向速度则低于锥角为18°和30°旋流器内的切向速度。

图7 截面处切向速度变化曲线Fig.7 Variation curve of tangential velocity at section
图8 示出的轴向速度反应了两截面的流体在2 个出口间的流动情况,轴心处的波峰表现了一级溢流管内流体做内旋运动,流体在向总溢流口处流动。在靠近旋流器壁面的地方,由于流体与壁面间的摩擦阻力,旋流器的轴向速度有明显的降低趋势。对比图8(a)(b),可见在截面二处,径向位置范围为10~20 mm 之间,流体有明显的回流或轴向速度减慢的现象,综合图6,更能说明流体的回流运动。而靠近旋流器外壁面处,二级稳流锥角为12°和24°的旋流器,液体的轴向速度明显高于另外两种旋流器。

图8 截面处轴向速度变化曲线Fig. 8 Axial velocity change curve at section
由图9(a)可见,截面一处流体基本都向中心汇聚,且二级稳流锥角为12°和24°的旋流器,汇聚的速度更快。而在截面二处,如图9(b)所示,中心处流体都有向外扩散的趋势,可见此时油核也基本稳定。图10 示出溢流压降ΔP1与底流压降ΔP2随二级稳流锥角θ3变化曲线,可见,ΔP1和ΔP2变化趋势基本一致,且并不随θ3变化而单调变化。旋流器效率提高时,压降也随之增大,且ΔP1比ΔP2增长更多,可见ΔP1更有利于中间油核从溢流口的排出,进而增大效率。

图9 截面处径向速度变化曲线图Fig.9 Radial velocity change curve at the section

图10 溢流与底流压降随二级稳流锥角变化曲线Fig.10 Pressure drop curve with θ3
由油相体积分数、速度场和压力降随θ3的变化规律可见,特定的二级稳流锥角(θ3=12°)下,在二级稳流锥角的外壁面不会产生循环流,且在总溢流口上方会产生回流现象,从而提高旋流器效率。
5 试验验证
加工轴流式两级一体化水力旋流器试验样机,研究分流比对油水分离效果的影响,试验工艺流程如图11 所示。基于数值模拟,调节与溢流口、底流口连接的阀门控制分流比分别为25%,27.5%,30%,32.5%和35%。为减少操作误差对结果造成的影响,每个操作参数下取样3 组,通过测油仪对入口及底流样液的含油浓度分别进行测量,取3 组的平均值作为最终含油浓度,分离效率计算式为:

图11 验证试验工艺流程示意Fig.11 Schematic diagram of validation test process flow
式中,F 为分流比;Ci,Cd分别为入口和底流口含油浓度,mg/L。
试验得出分流比与分离效率间的关系曲线如图12 所示。

图12 分离效率Ez 随分流比F 变化曲线Fig.12 Curve of Ez versus F
对比可见,试验与模拟的效率随分流比变化均成二次曲线关系(二次多项式拟合度R2均高于0.95),基本在分流比为32.5%时效率值最高;分离效率的试验值整体比模拟值低,但试验值与模拟值整体变化趋势一致,仅在分流比较低(低于27.5%)时二者误差较大,在较高的分流比(高于35%)时二者的误差有进一步增大的趋势;在分流比为27.5%~35%范围内试验值与模拟值拟合较好。试验验证结果表明:旋流器系统试验值与模拟值的变化规律基本一致,在设计分流比分布范围内二者相差不大,基本在误差要求范围内,一定程度上验证了数值模拟结果的可靠性。
6 结论
(1)通过对9 种结构参数的数值模拟优选,初始模型的质量效率为57.38%,溢流压降为31.18 kPa,经优化后,旋流器最高效率可达到96.38%,溢流压降为89.42 kPa。
(2)系统对比各结构参数对旋流器分离效率的影响,确定了最佳结构参数,具体为一级到二级距离L3=45 mm、一级导流锥锥角θ2=60°、一级溢流管内径D4=10 mm、一级螺距L2=90 mm、二级螺距L5=40 mm、二级导流内锥锥角θ4=30°、总溢流管内径D4=20 mm、总溢流管伸入长度L7=120 mm、二级稳流锥锥角θ3=12°。
(3)旋流器二级稳流锥角结构参数变化对分离效率的影响最为明显,影响规律为先减小后增大然后再减小的趋势,其中二级稳流锥角为18°和30°时,二级稳流锥角上部会形成不同程度的循环流,从而影响二级螺旋分离的流场,旋流器质量效率降低;二级稳流锥锥角为12°和24°时,总溢流管入口外壁处会产生部分液体的回流,从而可提升旋流器的质量效率,旋流器质量效率相对更高,其中最高为12°锥角时的96.38%。
