融合仿真模型与数据的水下节流阀冲蚀速率预测方法

李泽华，王泓晖，赵天昊，田晓洁，刘贵杰

（中国海洋大学 工程学院，山东青岛 266000）

0 引言

在水下采油树中，水下节流阀可被视为系统的核心，通常用于在稳态生产和瞬态流动情况下，控制碳氢化合物生产流量以及气体和水的注入。在实际生产活动中，石油和天然气流动时携带的沙粒将会对水下节流阀造成严重的冲蚀损坏，对于笼套式水下节流阀，其冲蚀失效行为主要发生在笼套部件，而过大的体积损失将导致笼套式水下节流阀功能失效，引发水下生产系统停机事故，且该系统的服役工况特殊，维修难度大，维修费用高，为此有必要探究水下节流阀冲蚀过程的预测方法，适时制定维护策略，保障水下生产过程的顺利进行。

针对水下节流阀的冲蚀预测方法，国内外学者展开了许多研究工作，GHARAIBAH 等［1］基于CFD（Computational Fluid Dynamics）分析节流阀中流体和颗粒流动特性，提出了预测节流阀冲蚀退化的方法，讨论了预测与试验结果之间产生差异的原因主要是忽略了因冲蚀引起的节流阀阀体结构变化。HU 等［2］采用CFD 方法研究了节流阀开度、钻井液流量、钻井液密度、固体颗粒质量流量等钻井参数对节流阀冲蚀特性的影响，并得到了固体颗粒对节流阀壁的冲蚀主要发生在阀芯端部等较有价值的结论。WALLACE 等［3］对流量系数和冲蚀速率进行了试验研究，强调忽视冲蚀引起的阀体表面演变建模可能是冲蚀速率预测不佳的部分原因［4］。可以看出，利用CFD 进行冲蚀预测是一种合理且有效的方法，但大多数研究在利用该方法分析时，忽略了阀体材料表面在实际冲蚀作用下发生的材料去除现象，而该现象将会导致颗粒碰撞角、壁面受力情况和局部流速发生改变，从而将颗粒重新引向另一个冲蚀“热点”，导致冲蚀速率随之改变，加速了冲蚀过程，而其又反作用于冲蚀过程，二者的相互作用形成了冲蚀退化的动态演变过程，从而导致数值模拟结果与实际情况存在差异。

针对上述问题，本文考虑了笼套式水下节流阀在冲蚀作用下的动态演变过程，以冲蚀试验样本的表面演变特征为依据，更新有限元模型并进行冲蚀过程仿真，构建不同冲蚀状态下的笼套式水下节流阀冲蚀仿真模型，最后利用RBF 神经网络对冲蚀仿真结果进行数据融合，建立笼套式水下节流阀融合冲蚀退化动态演变的冲蚀速率预测模型，以提高冲蚀速率预测的准确率。

1 研究对象及其数值模型

1.1 研究对象

为了研究水下节流阀的冲蚀退化动态演变过程，本文选用笼套式水下节流阀作为研究对象，水下节流阀笼套如图1 所示。在仿真环境中，选择密度为867.5 kg/m3、动态黏度为0.05 kg/（m·s）的原油。颗粒固体为陶瓷砂，粒子的平均直径为0.002 75 m，体积密度为2 670 kg/m3，假设节流阀内的流体为不可压缩湍流［2］，研究对象内部结构示意如图2（a）所示，再结合布尔运算对笼套式水下节流阀的内部流场进行抽取，抽取后进行网格划分，经过收敛性分析最终采用最小网格数1 315 109 个，其网格模型如图2（b）所示。

图1 水下节流阀笼套Fig.1 Underwater throttle valve cage

图2 节流阀内部结构及模型网格划分Fig.2 Internal structure and model meshing of throttle valve

1.2 水下节流阀冲蚀退化仿真模型

笼套式水下节流阀的冲蚀损伤是由于油气资源在开采过程中，流体从井内携带的泥沙颗粒对阀体不断冲击引起的材料脱离，是一个受多种因素协同影响的复杂过程。已有众多学者针对不同材料和不同工况建立了冲蚀模型［5-8］，本文使用Alhert 提出的冲蚀经验式（1）对笼套式水下节流阀冲蚀过程实施分析与计算：

式中，Er为冲蚀率，kg/（m2·s）；Np为与壁碰撞的固体颗粒数，无量纲；˙m为固体颗粒的质量流量，kg/s；C（dp）为固相颗粒粒径的函数，计算式见式（3）；f（α）为固体颗粒碰撞角α的函数，计算式见式（2）；v 为固体颗粒相对于壁面的速度，m/s；b（v）为固体颗粒相对速度的函数；Af为撞击阀体表面的单位面积，m2。

根据阀体材料和文献［9］中颗粒碰撞规律，对其进行定义：

式中，x，y，z 为常数，其参数选取见表1；dp为颗粒的直径，m；HB 为布氏硬度；FS为颗粒的形状因子，球形颗粒的形状因子为0.2。

表1 参数选取Tab.1 Parameter selection

1.3 边界条件设定

本文中仿真模型采用恒定速度入口边界，离散相选取Escape 边界条件；出口采用流量边界，离散相选取Escape 边界条件；选取标准壁面边界条件（Wall），颗粒和壁面选择反射（Reflect）类型；仿真计算模型进口采用速度边界条件，出口采用压力出口边界条件，湍流模型采用Standard 模型，压力修正Simple 算法分别建立了连续相的仿真模型和求解方法，边界条件见表2。

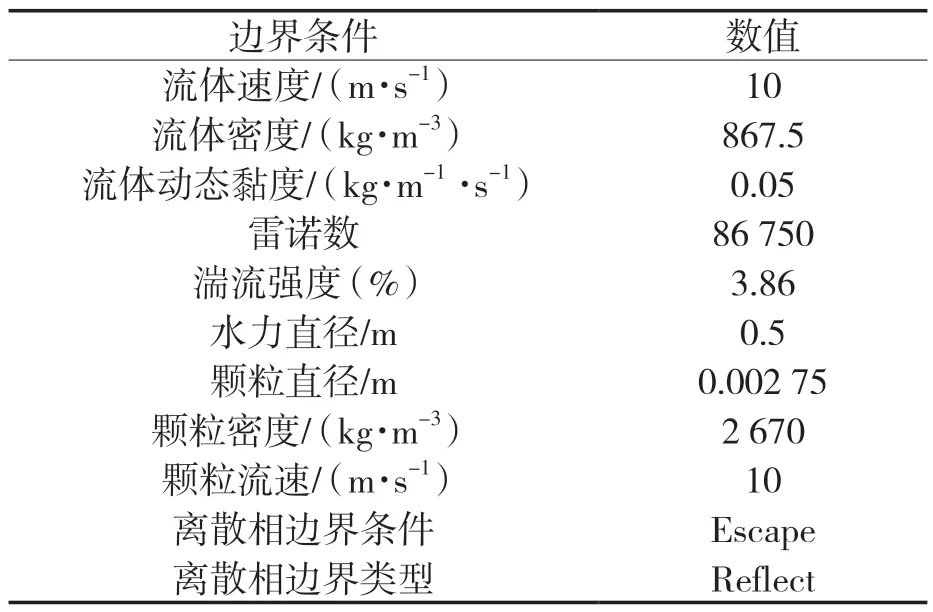
表2 边界条件设定Tab.2 Boundary condition setting

2 冲蚀试验

本节将对水下节流阀的笼套部件进行冲蚀试验，试验设备如图3 所示。选择XLT3325IR 柱塞泵空压机对试验油液进行增压，采用威尔泰流量计对管道内油液流量进行监控，用威尔泰温控仪、WL-801 压力变送器和WL-LWGA 流量变送器对试验油液在流经笼套式节流阀前后的压力、温度和流量变化进行监控，为避免信号不同步造成的误差，数据采集卡同步采集压力、流量和温度数据。油液流经装有密度为2 670 kg/m3的陶瓷砂箱后，将携带砂砾对水下节流阀笼套部件进行冲击，最终经过滤网过滤流回油箱，由控制器控制节流孔开度，砂砾流量通过沙箱出口处流量控制器调节。本试验将对水下节流阀在冲蚀时间为3 600 s、5 400 s 和7 200 s，3 个时间节点的压力差、温度变化、流量变化、笼套部件质量损失以及对笼套部件各个节流孔处的冲蚀凹陷深度进行测量并记录试验数据，进行3 组重复试验。

图3 冲蚀试验示意Fig.3 Erosion experimental schematic

3 数据与表面演化模型虚实融合方法

本文以笼套式水下节流阀在不同冲蚀时间下的冲蚀深度变化特征为阀体有限元模型的更新依据。在冲蚀过程中，颗粒速度Vp在冲蚀区域的中心降低到零，厚度损失较小，该部位被称为驻点，随后颗粒速度在目标表面附近径向增加，导致高度腐蚀Er 区域［10］为颗粒撞击阀体表面时的冲击角度，如图4 所示。

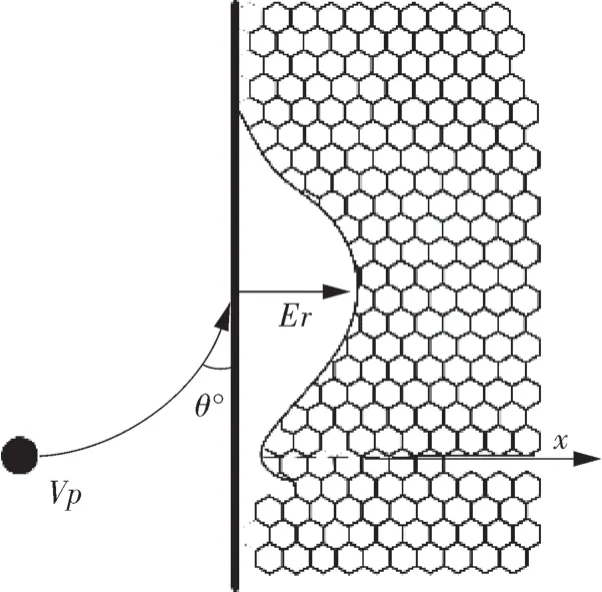
图4 颗粒表面冲蚀原理示意Fig.4 Schematic diagram of particle surface erosion

本文对笼套式水下节流阀融合冲蚀退化动态演变的有限元模型建立方法如下：首先，采用触针式表面轮廓仪分别对水下节流阀的笼套部件在3 600，5 400，7 200 s 时的冲蚀深度变化数据进行提取，建立冲蚀凹陷深度曲线，如图5 所示，可以看出在5 400～7 200 s 中，1 号节流孔受冲蚀作用影响，其深度变化趋于缓和，对于3 号节流孔而言，在这一冲蚀时间段中冲蚀面积扩大速度和冲蚀深度加深程度均高于1 号节流孔处。

图5 不同时间1 号、3 号节流孔冲蚀深度变化Fig.5 Erosion depth change of No.1 and No.3 orifices at different times

其次，运用SolidWorks 在VB 中进行二次开发，构建多个随冲蚀过程演变的水下节流阀笼套部件有限元模型如图6 所示。在编程过程中首先打开该模型，其次对该模型的尺寸参数通过SolidWorks 中的草图尺寸驱动变量，将模型尺寸参数与VB 界面中的文本框建立联系，并对参数赋值，从而对水下节流阀笼套部件在不同冲蚀时间下的有限元模型进行更新。

图6 SolidWorks 二次开发流程Fig.6 SolidWorks re-development flow chart

本文根据不同冲蚀时间下的节流孔冲蚀凹陷深度建立水下节流阀笼套部件表面演变模型，如图7 所示。在前7 200 s 的冲蚀过程中，冲蚀点处质量去除最多，受冲蚀影响较为严重的部位主要集中在笼套部件上的1 号和3 号节流孔，这与本文第3 节的数值仿真模拟结果相吻合。

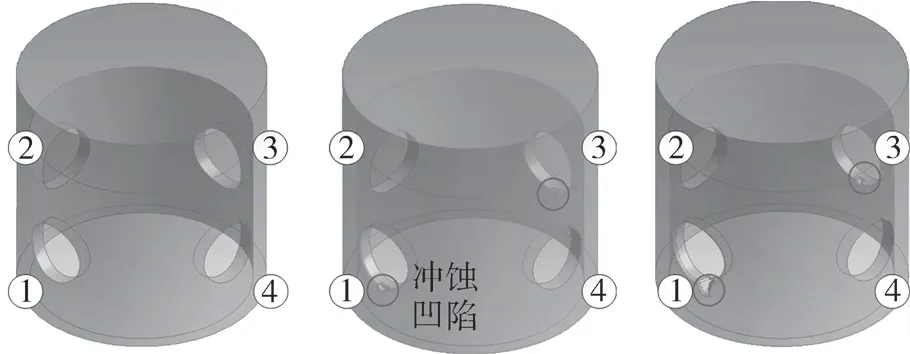
图7 笼套模型有限元模型更新Fig.7 Updating of finite element model of cage model

由笼套式水下节流阀在3 600～5 400 s 的冲蚀情况可得，位于入口管道处的1 号节流孔受冲蚀作用影响最为严重，主要是由于油液在从入口管通道经过节流孔，进入阀腔的过程中，由于节流孔的阻碍作用，1 号节流孔孔壁受到油液与其携带砂砾的冲击最大，阀体材料去除量最多，3 号节流孔内壁受到入口通道的流体与砂砾冲击影响与冲蚀面积扩张速度次之。

对在冲蚀过程中的水下节流阀的笼套部件每隔300 s 进行一次称重，记录其质量损失变化并通过下式计算冲蚀速率：

式中，ΔM 为水下节流阀的笼套部件在冲蚀作用前后的质量之差，kg，T 为冲蚀时间，s。

由式（5）得出笼套式水下节流阀冲蚀速率试验数据，作为第4 节中笼套式水下节流阀融合冲蚀退化动态演变的冲蚀速率预测模型预测结果的衡量标准。下文将对本节所建立的融合冲蚀数据的不同时间尺度、不同阀体表面形貌下的模型进行冲蚀仿真试验，并对其仿真结果进行分析。

4 数值模拟试验与结果分析

本节利用ANSYS FLUENT 仿真软件，对不同时间尺度、不同表面形貌的笼套式水下节流阀有限元模型进行仿真试验和结果分析，讨论笼套式水下节流阀在不同时间尺度下，以阀体表面形貌演变为自变量时，对内部流场的冲蚀速率和节流压差的影响，并利用笼套式水下节流阀数值模拟试验，建立融合冲蚀作用动态演变过程的笼套式水下节流阀冲蚀速率数据集。

4.1 水下节流阀内部冲蚀特性

本文对水下节流阀在结构完整、冲蚀1 h 含缺口和冲蚀2 h 含缺口3 种情况的冲蚀过程进行了分析，研究了当水下节流阀阀体表面结构发生改变时，对冲蚀速率的影响。图8 示出了水下节流阀3 号节流孔处的冲蚀速率云图。可以看出水下节流阀在工作过程中，当入口速度、流体密度、固体颗粒密度等对冲蚀速率影响较大的因素不变的情况下，受冲蚀作用影响最大的部位为笼套部件的节流孔。

图8 水下节流阀笼套冲蚀云图Fig.8 Erosion contour of underwater throttle valve cage

从图9 中可以看出，在冲蚀时间一定时，笼套式水下节流阀在冲蚀作用下，阀体表面出现缺口后的总体冲蚀速率低于笼套式水下节流阀结构完整时的冲蚀速率，即阀体受到的冲蚀作用发生材料去除时，冲蚀作用将被导向下一个“热点”部位，由此可以看出，笼套式水下节流阀在流体冲蚀作用下发生的材料去除对于冲蚀作用研究有着不可忽略的影响。

图9 3 种表面下的冲蚀率变化Fig.9 Erosion rate change under three surfaces

4.2 水下节流阀内部流场压力特性

本文对笼套式水下节流阀内部流体压力分布情况进行了分析，其压力分布云图如图10、11 所示。流体从入口管道到进入阀腔区域时一直为正压，当流入阀腔内部时，由于受到节流孔的阻碍作用，压力增大到7.12×104Pa，同时在节流孔附近产生回流区域，当流体流入节流孔后时，阀芯内部的压力有所下降，达到1.88×104Pa，当流体流入阀芯内部和出口管道时，其压力下降，并出现了负压。

从图10，11 中可以看出，与入口管道相连的笼套部件上的节流孔处受到的流体压力冲击最大，而受到流体冲蚀压力最为集中的部位，发生阀体材料去除的可能性相比笼套式水下节流阀的其他部位更大［11］。

5 面向有限元模型更新的冲蚀速率预测

本文在对笼套式水下节流阀进行基于冲蚀数据的模型更新之后，利用FLUENT 仿真软件对在不同时间尺度和不同表面形貌下的笼套式水下节流阀进行冲蚀仿真试验，本节将利用神经网络对冲蚀仿真试验数据进行拟合，以建立融合冲蚀退化动态演变的笼套式水下节流阀冲蚀速率预测模型。

本节将首先利用BP 神经网络对数据进行特征提取以及数据结构优化，对冲蚀仿真试验数据采集点之间的冲蚀速率进行数据补全与特征提取，其次，采用径向基函数（RBF）神经网络对冲蚀特征进行拟合，实现对笼套式水下节流阀在冲蚀过程中与流体相互作用，发生冲蚀退化动态演变时的冲蚀速率预测，为水下节流阀的预测性维护和早期微小故障诊断提供依据，其流程如图12 所示。

图12 水下节流阀冲蚀速率预测研究流程Fig.12 Flow chart of research on prediction of erosion rate of underwater throttle valve

5.1 数据采集

（1）本文对水下节流阀在冲蚀作用下的冲蚀速率数值模拟结果进行采集，对水下节流阀在时间为300 s 时进行一次采集，记录其冲蚀速率，数值模拟时间步为0.5 s，采集到的总数据集为R={R1，R2，R3}，其中R1，R2和R3分别为水下节流阀在时间为3 600，5 400，7 200 s 内的数据。

（2）将数值模拟冲蚀速率数据样本输入BP 神经网络中，由于本数值模拟采集的数据样本较少，故本文采用具有输入层、隐藏层和输出层的3 层BP 神经网络结构，最后输出特征值为{x1，x2，…，x46}。

5.2 预测结果与分析

根据RBF 神经网络具有拓扑结构简单、逼近能力强、不易陷入局部极小点及鲁棒性好等优点［12］，本文将利用RBF 网络对数值模拟所获得的冲蚀速率进行数据拟合，并得到输出值和试验数据的误差，再根据均方误差最小原则，求出输出层的权值；最后，根据样本信号对隐藏层和输出层进行权值校正，以提高输出函数的逼近精度，由此来进行笼套式水下节流阀冲蚀速率的数据回归预测。由该模型输出的结果为X={X1，X2，…，X23}，选取数据集的70%作为样本训练集，30%作为测试集，采用均方根误差（RMSE）来判定模型的准确性，其模型预测结果如图13，14 所示。

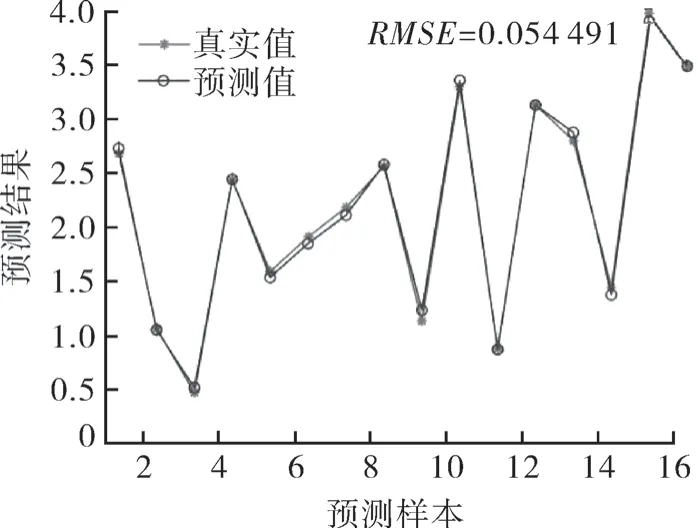
图13 RBF 神经网络训练集预测结果对比Fig.13 Comparison of RBF neural network training set prediction results

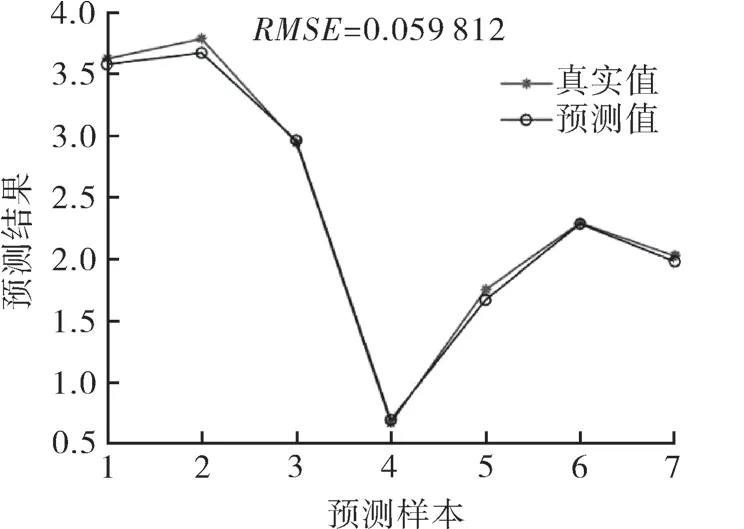
图14 RBF 神经网络测试集预测结果对比Fig.14 Comparison of RBF neural network test set prediction results

以通过式（5）得到的冲蚀速率为验证标准，从图15 中可看出，本文建立的笼套式水下节流阀融合冲蚀退化动态演变的冲蚀速率预测模型，经过充分学习和训练后，比传统的冲蚀速率仿真预测方法所得到的冲蚀速率预测值准确率提升了12.3%，体现了本文利用数值模拟与试验数据融合方法的有效性。

图15 冲蚀速率预测结果对比Fig.15 Comparison of erosion rate prediction results

6 结论

（1）本文通过虚实融合的方法，将仿真模型与试验结果相结合，建立了笼套式水下节流阀融合冲蚀退化动态演变的冲蚀速率预测模型。结果表明随着冲蚀的进行，阀体内壁面结构变化对于冲蚀速率预测准确率的影响不容忽视。

（2）通过对比发现本文所提出的基于数值模型与数据的水下节流阀冲蚀退化动态演变模型与传统冲蚀速率预测方法相比准确率提高了12.3%，由此可见本文所提出的冲蚀速率预测方法对水下生产系统节流阀生产维护与维修运营具有指导作用。

（3）在后续的研究过程中，笔者拟进一步对多个水下节流阀在水下采油树中的工况条件下进行重复试验，以收集水下节流阀在不同冲蚀阶段内的冲蚀退化信息，扩大样本容量，并对其进行数值分析，从而对所提出的笼套式水下节流阀融合冲蚀退化动态演变的冲蚀速率预测模型进行修正，提高模型的准确性，并且在水下采油树的实际工程应用中进行测试，提高模型的实用性。