小天体附着装置地形被动自适应机构设计与优化

贾山，李泽宏，吴明阳，梁思东，詹迪茜，陈金宝

（1.南京航空航天大学航天学院，南京 211106；2.航天进入减速与着陆技术实验室，南京 211106；3.深空星表探测机构技术工信部重点实验室，南京 211106；4.上海航天设备制造总厂有限公司，上海 200240）

0 引言

安全稳定的星表附着是开展小天体深度探测与开发的有效手段。在国内外为数不多的已执行和规划中的小天体探测任务中，只有中国的“天问二号”明确提出将进行基于附着的小天体采样（目标是一颗代号为2016HO3 的S 类小行星），是迄今难度最高的小天体探测任务，其余（例如美国的“欧西里斯”和日本的“隼鸟”等）大多采用“一触即走（Touch and Go）”的方式，不涉及复杂且危险的星表附着，在降低任务风险的同时，也降低了任务的科学回报。未来，随着小天体探测技术的不断发展，需进行星表附着的小天体探测任务将会越来越多。在此背景下，如何使附着装置更好地适应小天体星表地形，避免在抓附过程中附着装置与星表接触区域的岩石表面非结构性起伏形貌对附着装置甚至探测器本体位姿稳定性的影响，是在不增加附着装置机械臂结构及其位姿控制策略复杂度的同时保证相关任务成功实施的重要技术之一。

目前，在采用机构方式实现附着装置对非确知、非结构性小天体星表形貌特征的自适应方面，公开文献还很少。2019 年，王立武等［1］研制的爪刺附着系统采用了陀螺式姿态被动自适应方案，但采用基于附着过程中星表与附着装置之间接触力矩调整附着装置相对于星表姿态的方式，只能实现3个转动自由度对应的姿态偏转，未能实现对3 个移动自由度对应的位置偏移的自适应；2022 年，赵志军等［2］提出的小天体附着取样机器人可实现抓附、移动和取样等功能，但采用的是主动适应的方式，控制难度较大，作业周期较长，对复杂的小天体星表形貌的适应实时性不高。此外，学者们在对执行机构如何适应复杂作业界面方面的研究更多地体现在机器人研究领域。例如，文献［3］提出的设置于机械臂与工作面之间的串并混联机构可实现对工件表面不规则局部曲率的被动自适应，但只能实现3 转动和1 移动（3R1T）共4 个自由度的自适应，工作空间有限，适用性一般；文献［4］提出的核燃料组件微变形检测机构，通过在被检测工件与串并混联机构之间布置变异虎克铰自适应对中装置的方式，满足电涡流传感器与核燃料棒垂直对中检测要求，但同样只能实现3 转动和1 移动（3R1T）共4 个自由度的自适应；文献［5-8］分别对3-RPS、4-UPS-UPU、3-UPS+1-RPU 等并联机构的运动学和动力学建模方法、工作空间影响因素及其优化等问题进行了研究，但偏重于自由度的计算、优化模型的高效求解等方法论层面，可作为小天体地形自适应机构设计的理论参考。

综上所述，如何采用无源机构在3 转动和3 移动共6 个自由度上实现对非确知、非结构性的小天体星表地形的被动自适应，并通过几何参数优化的方式，扩大其工作空间，尚待进一步研究。针对上述需求，本文提出了一种6 自由度串3-RSPS 串并混联小天体附着装置地形被动自适应机构，完成了运动学分析与基于NSGA-II 算法［9-10］的工作空间多目标优化，获得了相较于目前广泛应用的3-SPS 机构更好的星表地形无源被动自适应能力，可供未来需要考虑星表地形自适应的小天体探测任务参考。

1 小天体附着装置地形被动自适应机构设计方案

1.1 目标功能

由文献［11-13］可知，绝大部分小天体无大气保护、体量较小、自转较快、密度较大，主要由碳质或硅质的矿石构成，赤道区域很可能存在米级的较大石块，风化层较薄，可作为附着作业的优选区域。结合上述星表形貌特征，受文献［14］所述爪刺-壁面接触模型的启发，可将期望的星表附着区域拟合为球面。如图1 所示，若附着装置与星表期望附着区域拟合球面未居中，伴随着收拢抓附动作，附着装置会受到所抓附星表岩石对其的不对称反作用力，从而发生偏移和扭转，且引起该偏转的干扰力∕力矩会沿机械臂对探测器本体的位姿稳定性造成影响，不利于任务的成功实施。

本文所提出的小天体地形被动自适应机构安装在探测器机械臂和附着装置之间，其目标功能可以图2 示意，即附着装置在附着前后与星表固定区域之间相对位姿的改变，可通过自适应机构本身空间位形的被动改变进行补偿，以减小对探测器机械臂空间位姿的影响。

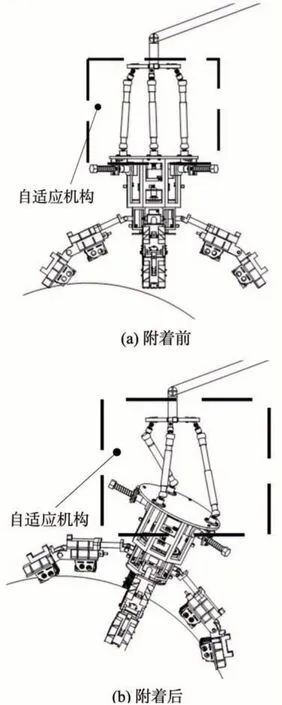
图2 自适应机构作业过程示意图Fig.2 Installation diagram of adaptive mechanism

1.2 设计方案

本文依据链内冗余应用［5-6］，提出了一种3-RSPS串并混联机构设计方案，如图3所示。

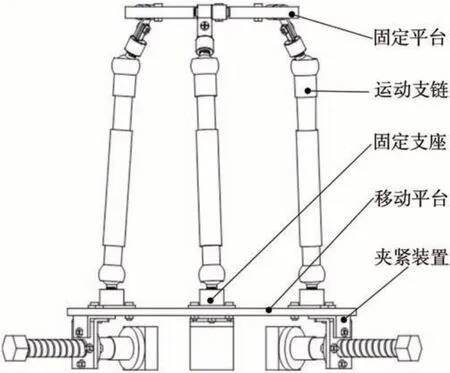
图3 自适应机构Fig.3 Adaptive mechanism

该机构由固定平台、运动支链、固定支座、移动平台和夹紧装置等部分组成。固定平台和移动平台通过三条均匀布置成120°的运动支链相连，而夹紧装置固定装在移动平台底板，通过手动夹紧方式固定连接附着装置。

固定平台以圆周120°设置U 形槽和半圆槽，用于固定运动支链。运动支链包括旋转阻尼器、滑杆阻尼器，从而实现被动自适应：当附着装置在附着过程中自身位姿产生变化时，通过自适应机构自身空间位形的被动变化来保证机械臂空间位姿的稳定，在此过程中，由运动支链的旋转阻尼器和滑杆阻尼器提供运动阻力，完成星表地形自适应的柔顺附着。

2 运动学分析

2.1 自由度计算

将自适应机构简化，如图4所示，机构活动构件总数为n=10，其中构件1～9 构成三条运动支链，构件10 为移动平台，构件11 为固定平台，即机架。运动副总数为p=12，以其中一条运动支链为例：构件10与构件1为球面副，构件1与构件2为移动副，构件2与构件3为球面副，构件3与构件11为球面副。

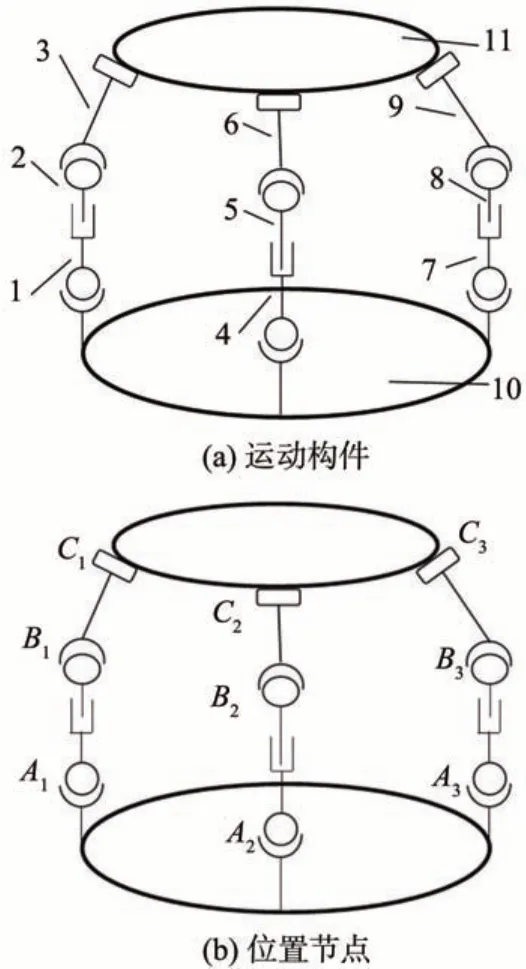
图4 结构简图Fig.4 Structure diagram

将根据修正的G-K公式对该机构进行自由度计算，即

式中：F表示机构的自由度数；n表示为构件的数量（包括机架）；p表示为运动副的数目；fi表示第i个运动副相对自由度数；ε表示并联冗余约束数；ξ表示局部自由度。

本文通过螺旋理论分析该机构冗余约束和局部自由度，进而计算整体机构的自由度［15］。首先针对一条运动支链进行分析，在A1B1C1分支链上建立坐标系C1-x1y1z1，如图5 所示。A1和B1点在坐标系中的坐标分别为A1（m4，m5，m6）、B1（m1，m2，m3）。

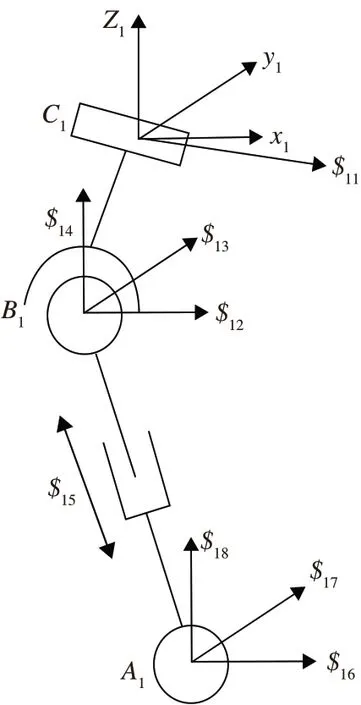
图5 运动螺旋分析Fig.5 Motion spiral analysis

将运动螺旋在普吕克坐标中表示为：

式中：k1，k2，k3是螺旋$ii的轴线方向数，k4，k5，k6是该螺旋对原点C1的线矩在x1，y1，z1三轴上的分量。

将自适应机构的运动支链及其对应坐标代入普吕克坐标中，得出运动螺旋系。以第一条运动支链为例：

由于上述运动螺旋系的秩为6，因此，约束螺旋为：

即，第一条支链对平台不施加约束，无冗余约束。同时从对应的普吕克矩阵中可以得出，该运动螺旋系存在两个线性相关的螺旋，即2 个局部自由度。由于其余分支链A2B2C2和A3B3C3同为一种结构，故整体机构无冗余约束，存在6 个局部自由度。代入式（1）中可得整机自由度为6。

综上，满足设计要求中的移动平台相对固定平台的六自由度要求。

2.2 运动学建模

为了方便求解移动平台的空间位置关系，研究移动平台的运动规律，建立静、动两坐标系。静坐标系OC-XCYCZC原点OC位于固定平台的几何中心，动坐标系OA-XAYAZA固定于移动平台，和移动平台一起运动，原点OA位于移动平台的几何中心。在移动平台没有运动时（即处于初始状态），动坐标系的XA、YA轴分别平行于静坐标系的XC和YC两轴。其俯视图如图6所示。

图6 坐标系Fig.6 Coordinate system

移动平台上任意一点H的位置可以通过坐标转换矩阵变换到固定平台的静坐标系上，即

为研究移动平台相对固定平台的运动规律，根据上述的坐标系，开展逆运动学分析，即根据结构参数和移动平台位姿参数，研究旋转阻尼器的转动角度和滑杆阻尼器的长度。

以一条支链为例，自适应机构的结构参数为移动平台半径R、固定平台半径r、固定支座的高度h以及旋转阻尼器长度L（即上述的构件9 长度）。滑杆阻尼器长度为L3（即构件7和构件8的总长），旋转阻尼器的转动角度θ3（构件9 相对机架11 的夹角），位姿参数为移动平台中心点的位置x0，y0，z0和动坐标系相对静坐标系的姿态角α，β，γ。

根据结构参数，在静坐标系中建立C1，C2，C3和B1，B2，B3铰接点坐标，在动坐标系中建立A1，A2，A3铰接点坐标。

A1，A2，A3这3点在静坐标系中的坐标通过式（3）进行坐标转换求得，具体如下：

式中：cα=cosα，sα=sinα，其他角度参数同理。N11为静坐标系中A1C1的向量，N12为静坐标系中B1C1的向量，其中

式中：N13为静坐标系中A1B1的向量，其他运动支链同理。

根据将以上的坐标、结构参数以及位姿参数代入，即可得出以下结果：

N12和N13，N22和N23，N32和N33三对矢量组合有唯一解，但每对组合的各自矢量存在无穷多个解，即Li和θi分别有无穷多个解，但它们的组合有唯一解。

2.3 运动学仿真验证

为验证运动学模型的准确性，进行简化模型的虚拟样机验证［7，16］。模型结构参数为：R=64 mm，r=44 mm，L=24 mm，h=16 mm。根据运动学模型，本文以运动支链的总长度作为仿真测量对象，并且在易产生干涉的零件之间设置接触力，仿真运行时间t为10 s。

针对各运动支链仿真，本文在移动平台的几何圆心处添加一个多自由度驱动，具体如下：

移动驱动：x0=10 · sin(t)，y0=10 · sin(t)

姿态驱动：γ=10°· sin(t)，β=10°· sin(t)

将三条运动支链总长度的理论曲线和虚拟样机仿真所得曲线进行对比，如图7和图8所示。

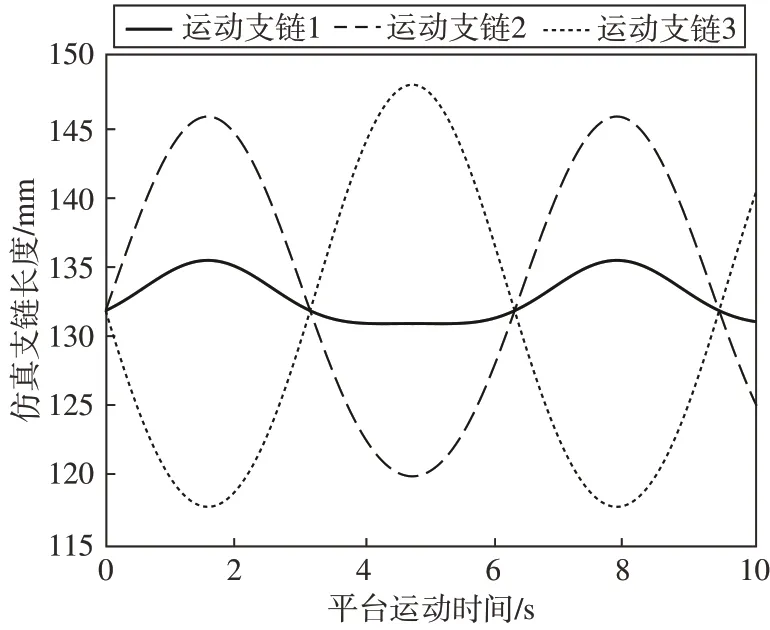
图7 仿真运动曲线Fig.7 Simulation motion curve

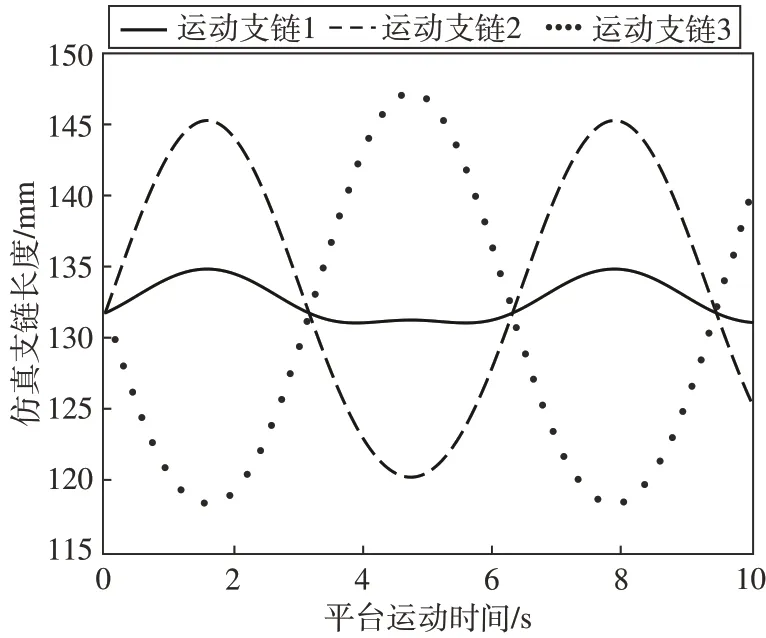
图8 理论运动曲线Fig.8 Theoretical motion curve

据图所示，所得到的仿真机构曲线与理论计算所得曲线的最大误差为0.07（理论曲线峰值与仿真曲线峰值之差∕理论曲线峰值），由机构装配误差引起，但仍在可接受误差范围内，验证了运动学模型的准确性。

同时，为验证机构自由度分析的正确性，本文进行正运动学仿真。选取各运动支链中的转动副和移动副作为主动输入。进行仿真后，进入后处理模块，可以得到移动平台质心沿初始动坐标系的x，y，z轴方向上的相对位移，如图9所示。

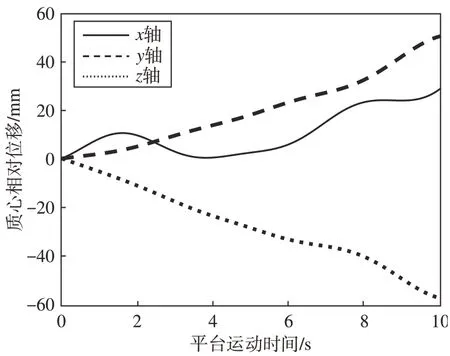
图9 质心位移曲线Fig.9 Centroid displacement curve

而后获取动坐标系的x，y，z轴相对静坐标系x，y，z轴的角位移曲线，并在同一坐标系下进行显示，如图10所示。

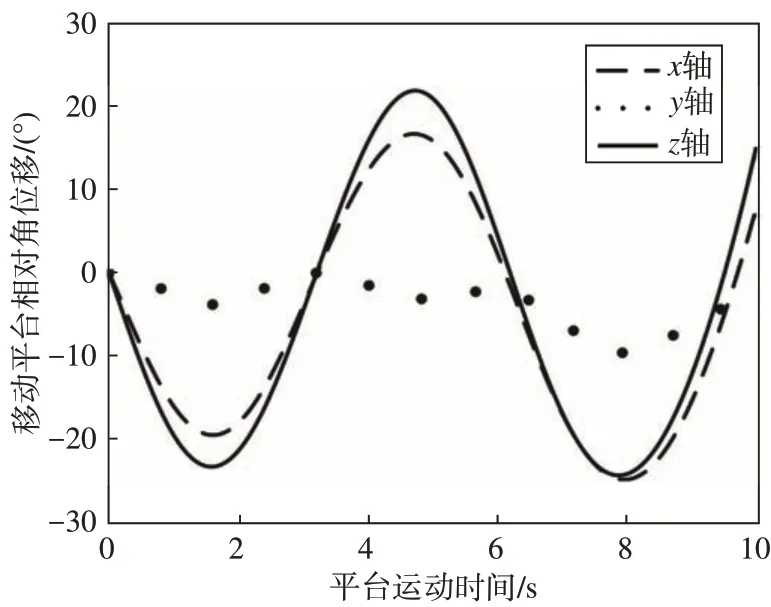
图10 移动平台姿态变化曲线Fig.10 Attitude change curve of mobile platform

观察图9 和图10 可得，移动平台沿初始动坐标系x，y，z轴方向上有明显的移动和偏转［7］。利用虚拟样机环境可得，自适应机构无冗余约束数和局部自由度，与理论公式分析结果保持一致，从而验证修改G-K公式分析自适应机构自由度的正确性。

3 工作空间分析

3.1 理论分析

本文采用数值搜索方法对自适应机构的定姿态工作空间进行分析。同时，在三支链并联机构中，由于3-SPS 并联机构应用较为广泛，本文将自适应机构与3-SPS 并联机构的相应工作空间进行对比［8］。

自适应机构的定姿态工作空间分析过程如图11所示。

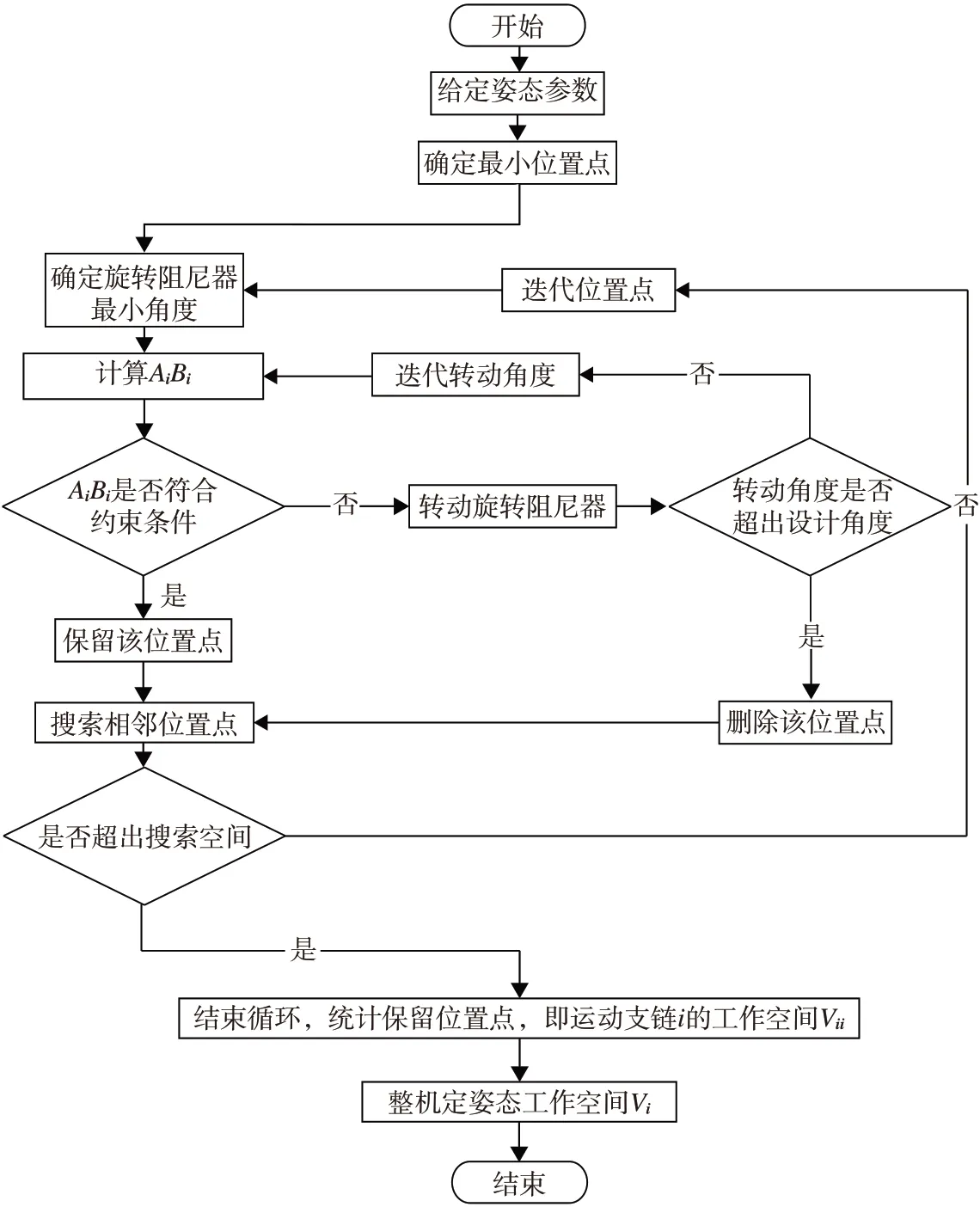
图11 定姿态工作空间分析流程图Fig.11 Flow chart of fixed attitude workspace analysis

3-SPS 机构工作空间分析流程与图11 相似，仅缺少转动角度的分析流程。在图11中，给定姿态参数和位置点为移动平台的位姿参数，所求的工作空间为移动平台中心点的可达位置集合。旋转阻尼器的转动角度Δθ和相邻位置点（Δx，Δy，Δz）的表达式如下：

式中：n由搜索精度确定，最小位置点（xmin，ymin，zmin）和最大位置点（xmax，ymax，zmax）由搜索空间确定，旋转阻尼器的最小角度θmin和最大角度θmax由结构参数确定。

给定姿态时，第i条运动支链的工作空间Vii和整机的工作空间Vi的关系如下：

针对图11的机构约束条件，影响机构的工作空间的结构参数包括滑杆阻尼器的活动范围、球铰转动范围和支链干涉。其中，自适应机构和3-SPS 机构均为三支链机构，结合机构运动情况和结构特性确定不会机构发生干涉，因此不考虑并联机构杆件间的干涉情况。

式中：Lmin为滑杆阻尼器活动最小长度，Lmax为滑杆阻尼器活动最大长度。θBi为球铰Bi角度，θAi为球铰Ai角度，θmax为球铰可转动最大角度。

3.2 实例计算

为与仿真模型参照，理论分析中的初始结构参数选取与虚拟样机仿真结构参数相同［7］，具体见表1。

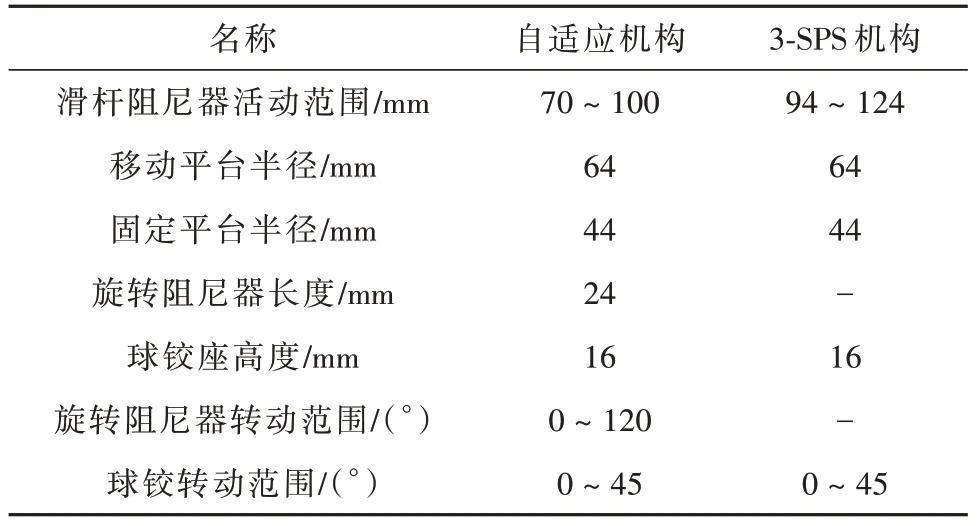
表1 初始结构参数Table 1 Initial structural parameters

仿真结果如图12 所示，3-SPS 机构的工作范围较大，但内部空心较多，体积为2.3×105mm3，自适应机构的工作范围较小，但内部空心较少，体积为2.64×105mm3。确定搜索空间如下（单位：mm）：x∈[-100，100]，y∈[-100，100]，z∈[-150，-50]

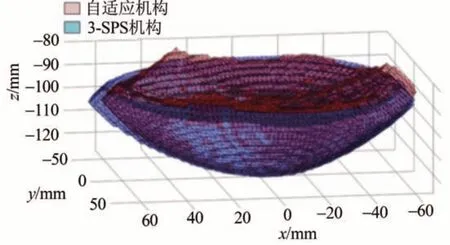
图12 初始姿态工作空间对比Fig.12 Comparison of initial attitude workspace

为简化全局工作空间的搜索，本文根据图11对自适应机构和3-SPS 机构的定姿态工作空间进行分析。

结果显示，3-SPS 机构最大工作姿态为［α，β，γ］=［100，30，26］（°），自适应机构最大工作姿态为［α，β，γ］=［88，34，36］（°）。相对3-SPS 机构，自适应机构的β和γ工作姿态角有明显提升，可适应更为陡峭的地形。

根据工作空间理论分析，定姿态工作空间Vi与全局工作空间W的关系如下：

式中：Vi为不同姿态下整体机构的工作空间。

结合上述最大工作姿态，对机构的全局工作空间进行仿真，设定搜索精度为2，结果如图13所示。

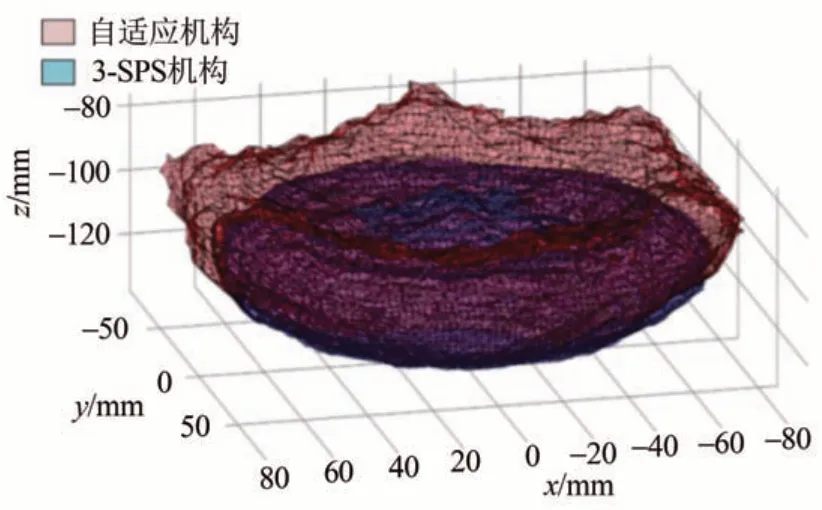
图13 全局工作空间对比Fig.13 Global workspace

仿真结果显示，3-SPS 机构的全局工作空间为4.43×105mm3，自适应机构的全局工作空间为6.24×105mm3，可见，自适应机构的全局工作空间囊括了3-SPS机构，相较后者提高了40.9%。

3.3 工作空间优化

为更大程度满足自适应机构的被动适应任务需求，需对机构工作空间体积进行优化。根据上述定姿态分析，工作空间和工作姿态存在竞争关系，因此将两者设为优化目标，进行多目标优化，优化流程如图14所示。

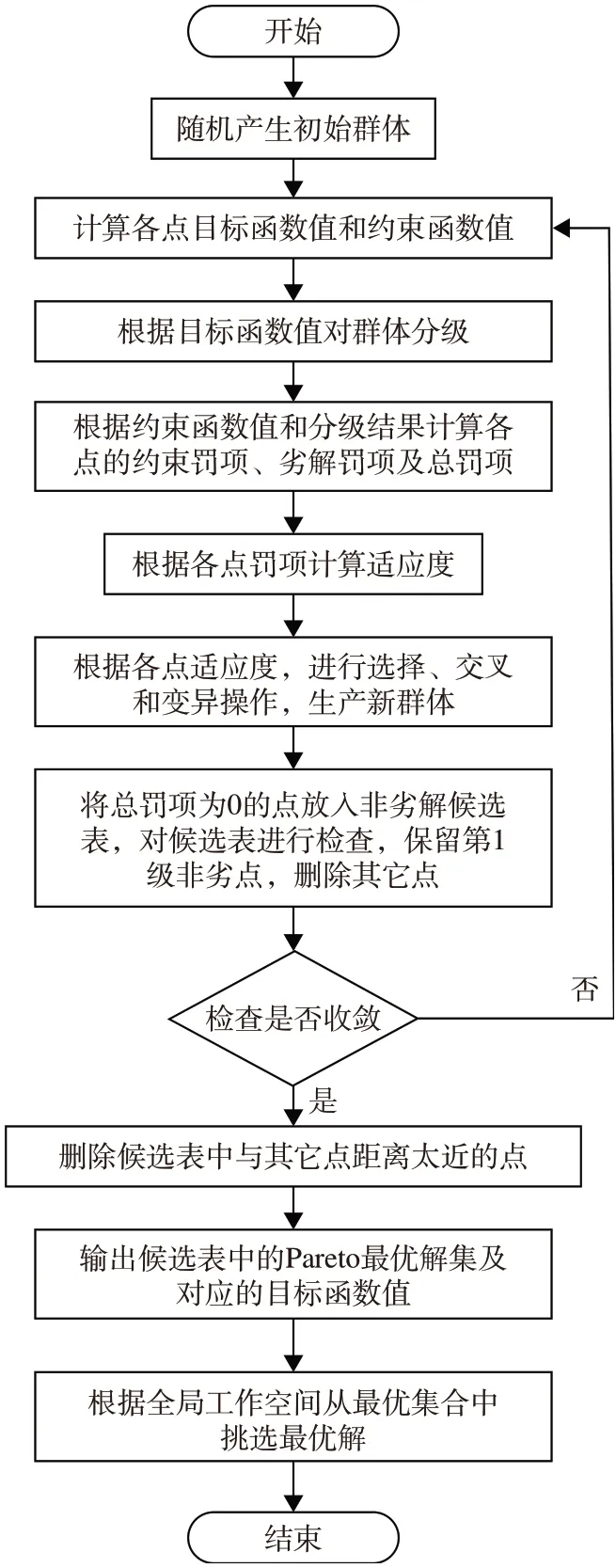
图14 多目标优化流程Fig.14 Multi-objective optimization process

优化目标为工作空间最大值、可活动β角最大值、可活动γ角最大值，约束条件为各运动支链的旋转阻尼器长度与最小滑杆阻尼器长度之比q1、旋转阻尼器的转动范围θi、移动平台和固定平台之比q2。

根据定姿态工作空间分析，为简化优化过程，设置目标函数如下：

目标1：minf1(X)=-V1

目标2：minf2(X)=-β

目标3：minf3(X)=-γ

式中：X=[x1，x2，x3，x4]T为优化变量，V1为初始姿态工作空间（mm3）。

结合尺寸设计，给出所优化变量的约束为：

式中：θL，θU分别旋转阻尼器的转动最小角度和最大角度，即θL≤θi≤θU。

由NSGA-II 算法得到的不同情况下Pareto 最优解［17］，如图15 所示。图中横坐标表示f1，即初始姿态工作空间；纵坐标表示f2或f3，即可活动角最大值（由于搜索结果的f2和f3相近，图中只显示其中一组）。

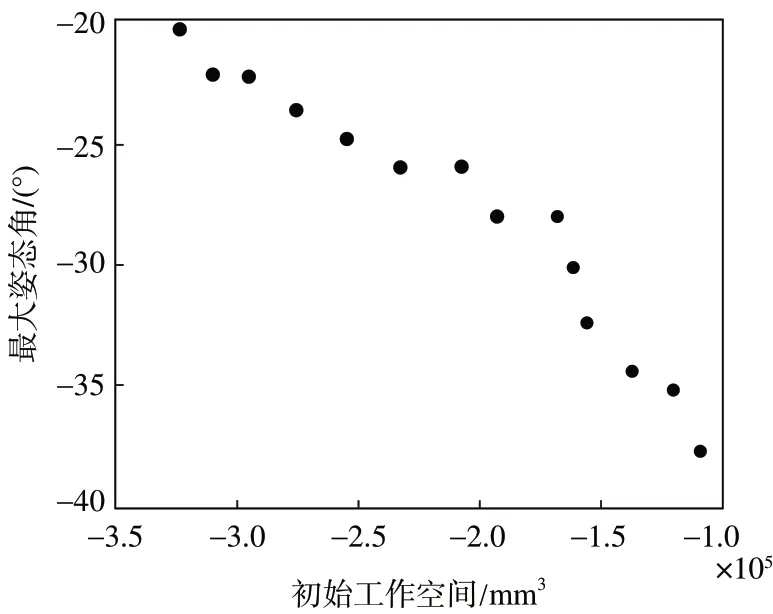
图15 最优解集Fig.15 Optimal solution set

经过50 代遗传算法优化，得出最终的最优解集，这些解经目标函数映射构成了优化任务的Pareto最前沿。

最优解集包含14 个最优解，而后根据上述全局工作空间分析方法，分别计算各个最优解所对应的全局工作空间，得出全局最优解为q2=0.502，θL=0.042，q1=0.277，θU=110.004，优化前后的主要构型和性能参数见表2。

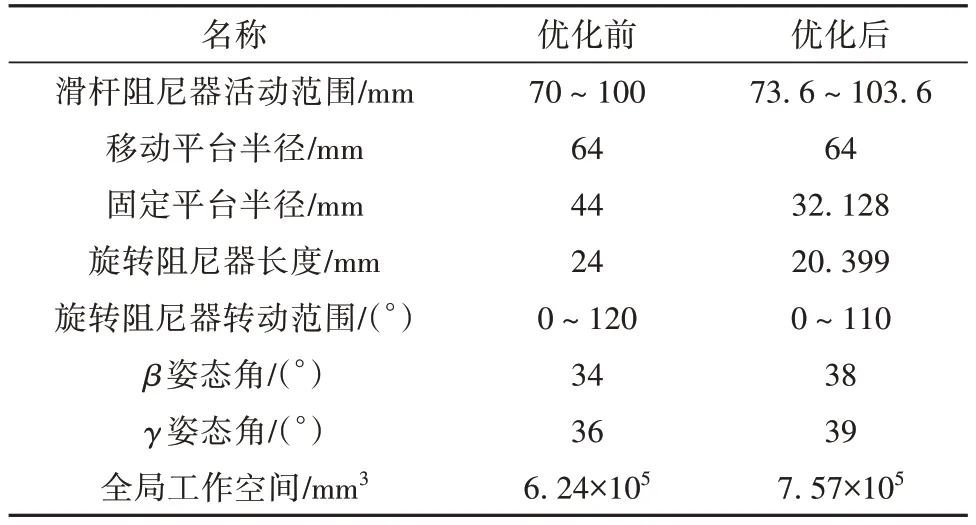
表2 优化前后构型与性能参数Table 2 Structural parameters before and after optimization

可知，在相同搜索精度下，优化后，全局工作空间为7.57×105mm3，提高了21.3%。

4 结论

为改善小天体探测器在星表附着过程中对非确知、非结构性星表地形的自适应能力，提高附着过程中探测器本体空间位姿的稳定性：

1）提出了一种基于3-RSPS 串并混联构型的小天体地形自适应机构，可实现附着装置在偏移和扭转共6个自由度上对星表地形的无源被动自适应；

2）建立了基于空间位置矢量法的运动学模型，通过G-K 公式验算了其具备6 个自由度，完成了以工作空间为自适应性能评价指标的整器构型优化；

3）相较于目前广泛应用的3-SPS并联构型，本方案的全局工作空间提高了40.9%，经过基于NSGA-II算法的多目标优化后，其作业过程中的整机尺寸包络优于ϕ300 mm×300 mm，全局工作空间可进一步提高21.3%，可适应更为崎岖陡峭的星表地形。