叉形光栅法产生分数阶涡旋光的实验探究

祁义红,杨 焓,王润兵,邢浩儒,王 鹏

(1.华东理工 大学物理学院,上海 200237;2.安庆师范大学 电子工程与智能制造学院,安徽 安庆 246133)

物理专业类课程在基础理论知识教学的同时,通过开展课程相关的拓展和创新实验探究,注重学生实践实验能力的培养和综合运用及创新能力的提升,是巩固和加深对理论认识的有效途径,对培养学生专业能力、提高学生综合素质和创新研究能力具有重要意义[1-3]。“光学”是应用物理和光电信息工程专业重要的基础核心课程之一,学科内容丰富、发展迅速、分支庞杂,尤其需要学生在基础课程学习阶段,打下坚实的理论基础,对光学的基本原理、思想和分析方法等建立起系统和清晰的物理图像[4]。衍射和光栅是基础光学课程和光学实验的重要内容,同时光栅也在如光谱分析等各类重要的光学器件和前沿研究中得到广泛的应用[5]。通过光学课程学习,学生已经认识到衍射光栅是由大量相互平行、等宽、等距的狭缝构成,利用光的衍射原理使光波发生色散的光学元件,广泛应用于光谱仪、摄谱仪等现代光谱分析设备中。通常物理实验中也开设了通过衍射光栅元件测量和分析入射光波长的实验[6-7],通过该实验学生对常规周期性光栅和光栅衍射有了一定的认识和清晰的物理图像。在此基础上进一步开展基于叉形光栅的衍射效应,研究携带轨道角动量模式的涡旋光产生,有助于促进学生对光栅衍射的进一步认识和理解,激发学生对涡旋光特性和光场调控的探索热情和兴趣。

光子具有自旋角动量(Spin Angulular Momentum,SAM)和轨道角动量(Obital Angular Momentum,OAM),分别与偏振和螺旋相位波前相关。涡旋光束是一种典型的OAM光束,其复振幅表达式中含有相位因子exp(ilθ),表明涡旋光束具有螺旋形的波阵面,螺旋相位由方位角相位相关项exp(ilθ)描述,轨道角动量量子数或拓扑荷数(Topological Charge,TC)为l,方位角为θ,每个光子的轨道角动量为lħ。1992年,Allen等人分别证明了涡旋光束具有轨道角动量和螺旋相位波前,光束中心为相位奇点,光场呈环形分布,中心光强为0[8]。涡旋光束是近年来国内外光学研究的热点,在光通信、量子信息、微小粒子操纵、光学成像等领域有重要的应用[9-12]。理论上,OAM模式提供了无限扩展的自由度,因而涡旋光束相比高斯光束大大增加了信息存储和传输的维度,拓展了通信信道容量[13]。涡旋光束携带的轨道角动量还具有机械效应,能够产生扭矩使物体移动或偏转,起到“光镊”或“光学扳手”操控微粒的作用[14]。

因此,如何产生各种不同类型的涡旋光引起了人们广泛的研究兴趣。目前常用的方法主要有模式转换法、螺旋相位板法、q-板法、计算全息法、超表面等各种不同方法和光学器件[12]。其中计算全息法又包括相位计算全息和叉形光栅计算全息,一般通过液晶空间光调制器加载计算全息图的方式对光场进行振幅和相位调制。本文采用叉形光栅方法,通过对入射的高斯光束进行衍射,分离出一级衍射光,即为相应轨道角动量为l的涡旋光。通过实验观察了分数阶涡旋光的产生,探讨和分析了左旋和右旋涡旋光束的光场分布特点。本文的实验探讨有利于学生进一步理解衍射效应和光栅性质及作用,认识光场轨道角动量和涡旋光束,培养学生对光学前沿探索和光场调控的研究兴趣。

1 实验光路

实验装置的光路原理图如图1(a)所示,选用795 nm的半导体激光器(Diode Laser,DL)作为激光光源,激光器输出光束为高斯光束,在激光器之后光路插入了一个衰减装置用来控制激光功率。L1和L2为两个凸透镜作为扩束装置,焦距分别为75 mm和175 mm,通过扩束可以方便后续对于光斑的每个部分分别进行调制。半波片(Half-Wave Plate,HWP)和偏振分束器(Polarized Beam Splitter,PBS)共同作用使其偏振态变为水平偏振的线偏振光。将线偏振光入射到空间光调制器(Spatial Light Modulator,SLM)上,通过SLM加载计算机产生的不同OAM值的叉形光栅或者相位全息图,从而对入射光束进行振幅或相位调制。反射镜M1用来调整SLM出射的光束方向。实验中引入4f系统相干滤波,L3和L4构成的4f系统做傅里叶变换及反变换。当经过L3透镜做傅里叶变换后的光束为不同的拉盖尔高斯模式时,模场光斑的大小可能会不同,通过可变孔径式孔径光阑相干滤波,选择出第一极大条纹,即可得到特定模式的拉盖尔-高斯光束衍射光。通过透镜L5对输出涡旋光束进行聚焦,以便获得更好的观测结果,最终可以在CCD(Charge-Coupled Device)相机上观测到一系列拉盖尔-高斯模式(Laguerre-Gaussian Mode,LG)的衍射图样。实验中采用的实验装置和实际光路如图1(b)所示。

(a)光路原理图

2 叉形光栅设计

叉形光栅主要有两种制作方法[9,12]:一种是利用平面波和LG光束干涉制备叉形光栅器件,另一种利用计算机生成全息图的方法产生叉形光栅。本文采用计算机全息法制作叉形光栅,通过计算平面波和LG光束干涉的光强分布生成全息图,在空间光调制器上加载全息图来模拟叉形光栅,如图2所示,通过叉形光栅衍射在远场分离出的一级衍射即分别为轨道角动量为±l的涡旋光。

图2 叉形光栅法生成涡旋光束

根据全息法的原理,当参考光照射到由物光和参考光干涉形成的光栅时,经一级衍射即可观察到物光。因而,当利用基模高斯光束作为参考光,目标涡旋光束为物光,通过计算机计算即可获得用于产生目标涡旋光的叉形光栅。这里起主要作用的是涡旋光的相位exp(ilθ)和和高斯光束的相位exp(-ikxsinα)在横向平面干涉的结果,其中l为拓扑荷数,k为波数,x为横向坐标,α为传播方向与z轴夹角,原理如图3所示。由图3可以发现,对于拓扑荷数为l的叉形光栅,上半部分比下半部分多了l条明条纹与l条暗条纹,产生了叉形图样,这正是由于相位叠加的原因。

图3 叉形光栅相位合成示意图

通过计算机程序计算进行模拟,可以方便地获得对应不同轨道角动量的叉形光栅,这相对于传统用激光干涉制备叉形光栅器件来说具有如灵活控制、无需相应材料等诸多优势。图4为通过计算获得的轨道角动量分别为-3.0、-3.2、-3.6、-3.9的叉形光栅全息图,可以发现对应不用轨道角动量的光栅分叉形状,以及在分数轨道角动量出现的叉形光栅错位。在计算出叉形光栅后,将光栅全息图加载到光路中的SLM,通过SLM对入射光场的调制,在SLM反射或透射的衍射光中分离出一级衍射光,即轨道角动量为±l的涡旋光。

图4 轨道角动量分别为-3.0、-3.2、-3.6、-3.9的叉形光栅全息图

3 涡旋光束的实验产生和测量

按图1所示搭建并调节光路,通过改变加载到计算机上不同拓扑荷数的叉形光栅,利用孔径光阑,在合适位置分离和观察一级衍射的涡旋光束。首先,实验产生和测量了l=1.0～4.0的整数涡旋光,结果如图5所示。从图5中可以看出,光场为涡环形分布,随着拓扑荷数增大,光中心暗斑增大,各环的宽度逐渐减小。由于反射角度的原因,此时涡旋光并不是呈现正圆环形分布,而存在一定角度的倾斜。可以预期的是,对于轨道角动量为±l的涡旋光来说,由于其旋向刚好相反,因而其光束倾斜的方向呈现对称分布,这在随后的实验中也观察到此现象。

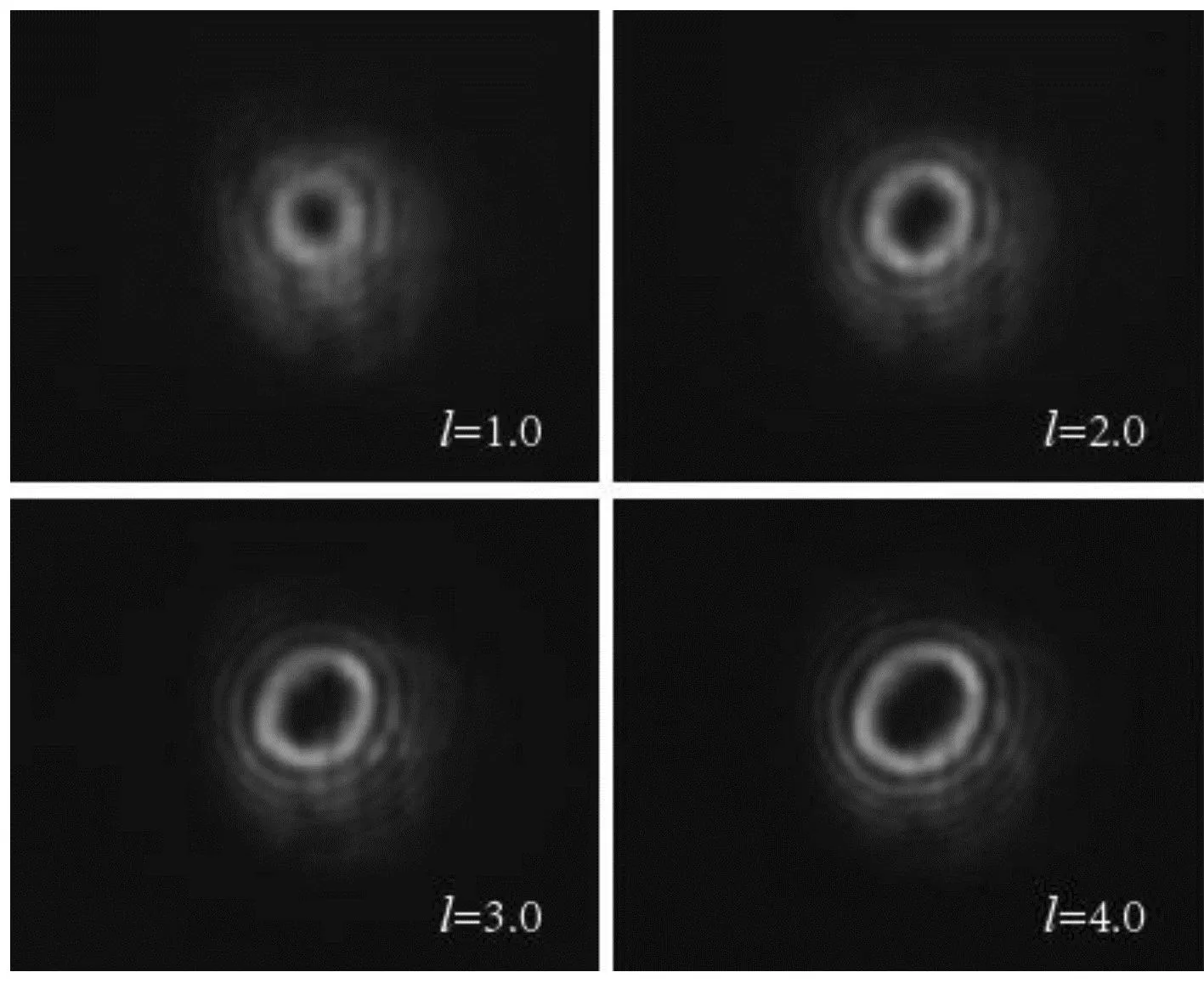
图5 实验探测的轨道角动量分别为1.0、2.0、3.0、4.0的涡旋光

分数阶涡旋光束极大地扩展了涡旋光束的轨道角动量模式的量子态空间,同时利用分数阶涡旋光束不同于整数阶涡旋光的光场分布和螺旋性,可以更精准地操控微小粒子,为材料科学和生物医学上的应用提供更好的光学手段[11]。近年来,国内外研究人员开展了很多关于分数阶涡旋光束的产生、探测及其在通信、成像等方面应用的研究[11,15-18]。为观察和分析分数阶涡旋光特性,我们设计了用于产生分数阶涡旋光的叉形光栅,实验测量了l=±3.0～±4.0的涡旋光如图6和图7所示。分数阶涡旋光束绕中心一周的相位变化不再是2π的整数倍,因而在存在分数轨道角动量的情况下不再呈现完整的圆环形状,而是出现了开口形状,缺口的大小于依赖于分数部分与相邻整数部分差值的大小。同时,从缺口的螺旋方向能明显的区分左旋和右旋的轨道角动量符号。分数阶涡旋光束能够极大的拓展基于轨道角动量模式的通信信道,特殊的光场分布和旋向也使其在微小粒子的光操纵上有重要的应用,本部分实验让学生进一步认识了分数阶涡旋光场及其通过叉形光栅的光场调控。

图6 实验探测的轨道角动量分别为3.0、3.2、3.4、3.6、3.8、4.0的涡旋光

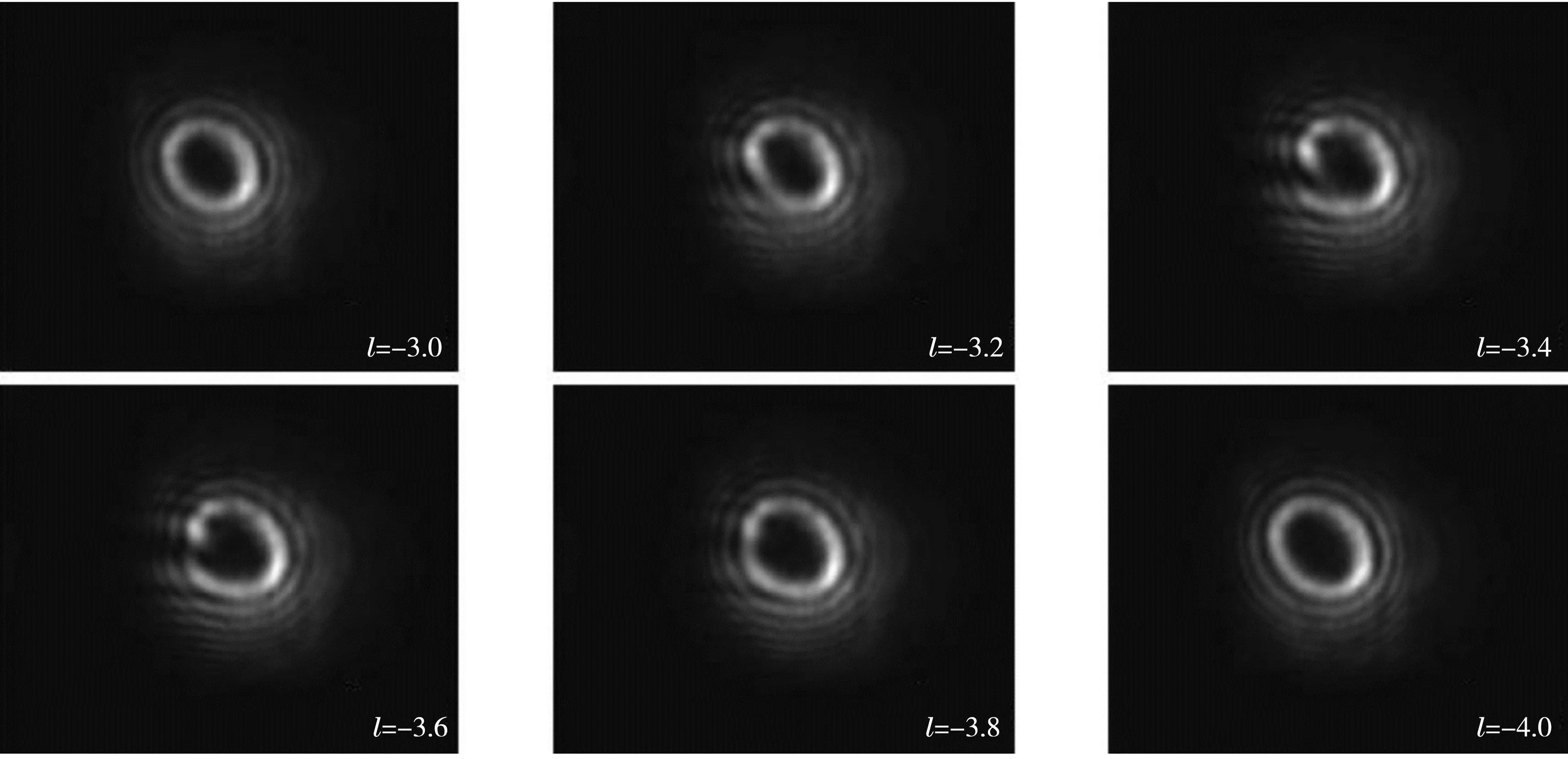
图7 实验探测的轨道角动量分别为-3.0、-3.2、-3.4、-3.6、-3.8、-4.0的涡旋光

4 结 论

本文利用空间光调制器,设计并开展了以叉形光栅衍射为基础的涡旋光产生实验。以分数阶涡旋光为研究对象,编写了叉形光栅的计算机程序,进一步加深了学生对光栅周期性结构的认识和理解。实验上通过光栅衍射效应产生和观测了分数阶涡旋光,分析了分数阶涡旋光的特点和强度分布,使学生对涡旋光的性质、轨道角动量和光场调控有了一定的认识。

通过本实验,学生进一步加深了对衍射和光栅特性的理解,激发了对光学课程学习、光学前沿研究和探索的兴趣,拓展了学生的光学专业知识,提高了学生的综合实验能力和开展创新探索实验的能力,有利于培养、提升学生的综合素质和创新意识。